Электропроводность электролитов-суспензий системы NaF-AlF3-CaF2-Al2O3

Разработка технологии использования малорасходуемых («инертных») анодов в производстве алюминия делает перспективными исследования по определению физико-химических свойств суспензий глинозема в низкотемпературных криолитоглиноземных расплавах с точки зрения применения их в качестве электролита.

Насыщенные по глинозему расплавы снижают температуру электролиза, значительно уменьшают скорость коррозии инертных анодов и обеспечивают более эффективное разделение продуктов электролиза, тем самым увеличивая выход по току [1]. В настоящее время уже существуют работы и патенты, предусматривающие применение электролитов-суспензий [2-6]. Физико-химические свойства таких электролитов детально не изучены [1].

Одним из важнейших физико-химических свойств электролитов является их электропроводность. Поэтому при реализации низкотемпературного электролиза необходимо знать, как меняется электропроводность электролитов-суспензий с их составом и температурой.

Данных по исследованию электропроводности криолитоглиноземных суспензий в литературе не найдено. Однако к настоящему времени построено множество моделей проводимости гетерогенных сред, результатом которых выступают аналитические выражения, связывающие проводимость среды с проводимостями включений, их концентрацией в суспензии и формой зерен [2,3]. Эффективная проводимость расплава, в котором однородно распределены частицы глинозема, можно рассматривать как частный случай таких моделей.

Максвелл [7] вывел уравнение для расчета эффективной проводимости χ смеси, состоящей из сфер с проводимостью /₀, окруженных сплошной средой с проводимостью x L :

X = 1

X

3 ф

^{2 +} X g / Xl ,   ’

--+ ф

¹ " X g / X l

где φ – объемная доля сферической фазы сфер, которая определяется как V

Ф = Vg + Vl ’ где VG и VL - объем сфер и среды соответственно.

Уравнение (1) значительно упрощается, если дисперсная фаза представляет собой непроводящие сферические частицы (в нашем случае частицы глинозема). Если x G / X L =“ , то уравнение (1) приобретает следующий вид:

X = 1

X l

2/ ф + 1

.

Целью работы являлось экспериментальное установление закономерности влияния дисперсного глинозема на удельную электропроводность криолитоглиноземных суспензионных расплавов системы Na3AlF6-AlF3-5 мас. % СаF2 - Al2O3. Необходимость этих исследований вызвана тем, что все существующие на данный момент математические модели созданы с условием, что непроводящие частицы имеют единый размер и сферическую форму, какими частицы глинозема считать, безусловно, нельзя.

Методика эксперимента

Для измерения электропроводности криолитоглиноземных суспензий применяли электрохимическую ячейку с двумя параллельными электродами, изображенную на рис. 1.

Ячейка состоит из корундового стакана (1), двух параллельно установленных электродов (4) и мешалки (5). Для экспериментов использовали корундовый стакан (1) с внутренним диаметром 55 мм и высотой 12 см. Электроды изготавливали из молибденовых пластин шириной 10 мм, высотой 40 мм и толщиной 0,5 мм.

Для поддержания суспензии во взвешенном состоянии между электродами в центр корундового стакана устанавливали титановую мешалку (5) c диаметром лопастей 40 мм, приводимую в действие электродвигателем (скорость вращения мешалки 8 об/c). Температуру в ячейке контролировали подключенной к многоканальному термометру хромель-алюмелевой термопарой (11), помещенной в корундовый чехол (9). Токоподводы к электродам и шкив мешалки, выполненные из нержавеющей стали, были защищены от воздействия агрессивной среды корундовыми трубками (6-8). Для уменьшения изменения состава исходных электролитов вследствие их испарения и гидролиза применяли шамотную крышку (2).

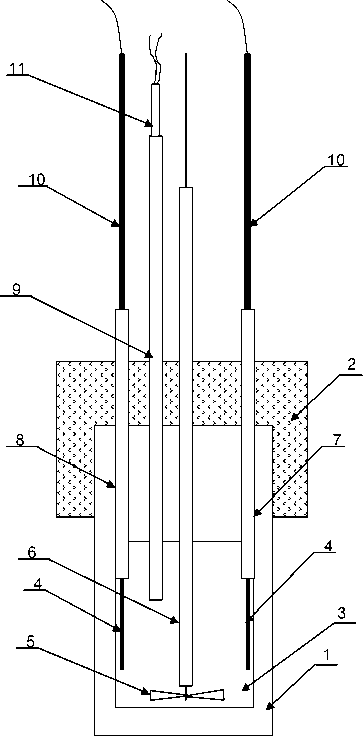
Рис. 1. Ячейка для определения электропроводности суспензий: 1 – корундовый стакан; 2 – шамотная крышка; 3 – электролит; 4 – молибденовые электроды; 5 – титановая лопастная мешалка; 6,7,8 – корундовые трубки; 9 – корундовый чехол; 10 – стальные токоподводы; 11 – термопара

Перед началом эксперимента корундовый стакан, содержащий предварительно наплавленный исследуемый расплав, помещали в печь и медленно нагревали. После того, как электролит расплавлялся, в него последовательно устанавливали мешалку, термопару, помещенную в корундовый чехол, и электроды. Расплав перемешивали непрерывно в течение всего эксперимента. После достижения требуемой температуры проводили пять измерений сопротивления и по среднему значению рассчитывали постоянную ячейки K (4):

K = R-x,                                             (4)

где R – электросопротивление электролита, Ом; χ – удельная электропроводность, См/см.

Значения удельной электропроводности криолитоглиноземных расплавов системы Na3AlF6-AlF3-5 мас. % СаF2 - Al2O3 без дисперсных частиц глинозема при соответствующей температуре рассчитывали по уравнению (5)[2]:

X = -3,662 - 9,908^10^-2 КО -3J4940^-2 w (AI 2 O 3 ) + 4,972-10 -3 Т               (5)

Таблица 1. Ситовой анализ проб глинозема Worsley (Австралия)

Содержание фракции, мас. % +140 мкм -140 +100 мкм -100 +74 мкм -74 +45 мкм -45 мкм 4,38 42,07 38,18 13,48 1,89 где X — удельная электропроводность, См/см ; w(Al2O3) - содержание Al2O3, мас. %; T -температура, К. Уравнение действительно при 2,0≥КО≥1,2, в интервале изменения содержания Al2O3 от 0 до 6 мас. %, и при перегреве над температурой плавления электролита без глинозема до 45 K. Коэффициент множественной регрессии для этой зависимости равен 0,9985 [8].

После определения константы ячейки в расплав добавляли навески глинозема заданной массы. После каждой добавки проводили пять измерений сопротивления электролита при фиксированной температуре и по среднему значению рассчитывали удельную электропроводность.

Во всех экспериментах по исследованию электропроводности суспензий использовали глинозем производства фирмы Worsley (Австралия). Для определения гранулометрического состава глинозема был проведен ситовой анализ методом сухого рассева, результаты которого даны в табл. 1.

Как видно из данных табл. 1, глинозем относится к песчаному типу, так как содержание фракции -45 мкм составляет менее 10 мас. % [3] и имеет довольно однородный гранулометрический состав (содержание основного класса 140 +45 мкм более 80 %).

Сопротивление электролита определяли по годографам импеданса, которые снимали с помощью потенциостата AUTOLAB. Импеданс определяли при помощи наложения потенциала переменного тока разной частоты на электрохимическую ячейку и измерения тока, протекающего через нее. Откликом на данный потенциал служил сигнал переменного тока, который записывали в форме диаграммы Найквиста [3].

Применение описанного метода и потенциостата с высокочастотным модулем, позволяющим изменять частоту в диапазоне от 1 МГц до 0,1 Гц, исключает влияние проводников и поляризационного сопротивления при измерении на высоких частотах.

Моделирование и оценка достоверности результатов экспериментов

Для оценки возможности применения описанной выше методики исследования электропроводности электролитов-суспензий были проведены эксперименты на водном 1М растворе KCl при различном содержании глинозема. Раствор хлорида калия был выбран, потому что его электропроводность достаточно хорошо изучена, глинозем в нем не растворяется, образуя суспензию. Результаты измерений представлены в табл. 2 и на рис. 2.

Из табл. 2 и рис. 2 видно, что с увеличением содержания дисперсных частиц удельная электропроводность суспензии уменьшается практически линейно. Отклонение (|∆|) значений χ, рассчитанных по уравнению Максвелла (3), от экспериментальных данных не превышает 3,5 %. Такое отклонение можно объяснить тем, что частицы глинозема имеют различный размер (табл. 1) и сложную геометрическую форму, отличную от сферической. Исходя из этого – 165 –

Таблица 2. Результаты измерений электропроводности водных электролитов-суспензий

Т эксп., К	Постоянная ячейки К∙102, см-1	Al 2 O 3 *, мас. %.	Al 2 O 3 ** об. %	Сопротивление, Ом	Удельная электропроводность, См/см		|∆|, %
					эксп.	расч. по урав. (3)
		0	0	2,6126	0,1098	0,1098	0
		5	1,23	2,6730	0,1074	0,1078	0,43
297	28,6968	10	2,43	2,7406	0,1047	0,1059	1,12
		15	3,61	2,8136	0,1020	0,1040	1,97
		20	4,76	2,9058	0,0988	0,1022	3,46

Примечание: * – содержание Al2O3 в электролите-суспензии; ** – % объема, занимаемый Al2O3 присутствующим в электролите в виде дисперсных частиц.

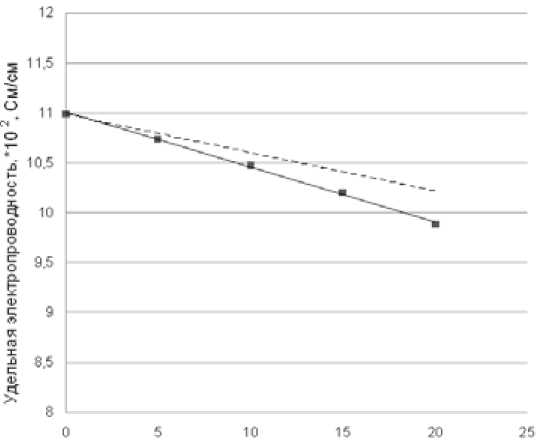
Содержание АкОз. мас.%

Рис. 2. Влияние содержания дисперсного глинозема на электропроводность 1М раствора KCl: сплошная линия – экспериментальные результаты, пунктирная линия – значения, рассчитанные по уравнению Максвелла (3)

можно сделать вывод, что описанная методика позволяет с приемлемой точностью исследовать электропроводность электролитов-суспензий.

Результаты экспериментов и их обсуждение

Измерения электропроводности электролитов-суспензий проводили в расплавах Na₃AlF₆-AlF 3 -5 мас. % СаF 2 – Al 2 O 3 в диапазоне КО от 1,2 до 2,0, при различном содержании дисперсного глинозема (от 0 до 13,2 об. %). Исходные составы электролитов без дисперсных частиц глинозема и их электропроводность при соответствующих температурах приведены в табл. 3.

Так как расплавы были насыщены по глинозему, то можно считать, что добавляемый в ходе эксперимента глинозем не подвергался растворению и все его частицы находились в расплаве – 166 –

Таблица 3. Электропроводность исходных криолитоглиноземных расплавов системы Na₃AlF₆-AlF₃-5 мас. % СаF 2 – Al 2 O 3

п.п.	КО	Al 2 O 3 , мас. %	Т эксп., К	χ, См/см[9]
1	2	6	1216	1,997
2	1,9	6	1201	1,932
3	1,8	6	1184	1,857
4	1,7	6	1163	1,763
5	1,6	6	1138	1,649
6	1,5	4	1112	1,592
7	1,4	4	1075	1,418
8	1,3	4	1030	1,204
9	1,2	3	1018	1,186

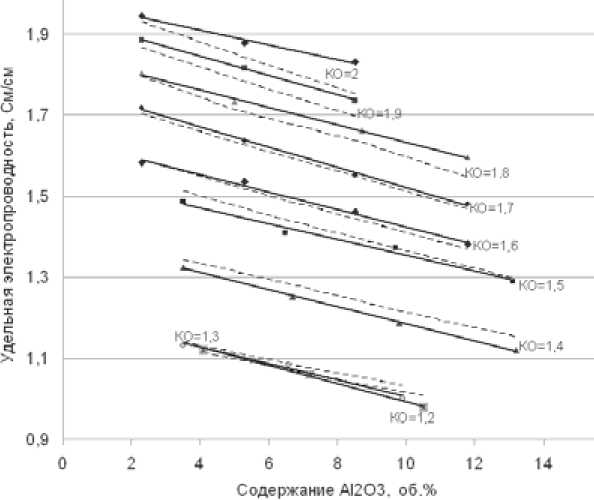
Рис. 3. Влияние содержания дисперсного глинозема на электропроводность расплавов Na3AlF6-AlF3-5 мас. % СаF2 – Al2O3 при изменении КО от 1,2 до 2,0: сплошная линия – экспериментальные результаты; пунктирная линия – значения, рассчитанные по уравнению Максвелла (3)

в виде суспензии. Объемную долю дисперсного глинозема в электролите-суспензии определяли по уравнению (2). Истинную плотность глинозема принимали равной 4 г/см3, а плотность расплавов без дисперсных частиц глинозема рассчитывали по уравнению (6), выведенному на основании экспериментальных данных для составов исследуемой области [3]:

ρ= 2,802+0,2427 ∙КО-125,1∙10^-4 ∙w(Al 2 O 3 ) – 115∙10^-5 ∙Т,

где ρ – плотность, г/см³ , w (Al₂O₃) – концентрация Al₂O₃, мас. %, Т – температура, °С. Коэффициент множественной регрессии для этой зависимости равен 0,95 [8].

На рис. 3 видно, что зависимости удельной электропроводности от содержания Al₂O₃ в суспензии имеют линейный характер с практически одинаковым наклоном для всех исследованных КО. При увеличении содержания дисперсного Al₂O₃ на 1 об. % удельная электропроводность в среднем снижается на 0,0215 См/см (∂χ/∂С Al2O3 = – 0,0215).

На основе экспериментальных данных получено регрессионное уравнение (7), описывающее зависимость электропроводности исследуемых электролитов-суспензий системы Na 3 AlF 6 -AlF₃-5 мас. % СаF₂ – Al₂O₃ от КО, содержания дисперсного глинозема и температуры (χ=f(КО, [Al 2 O 3 ], T)):

lnχ =3,53986 + 1,56∙10^-3∙КО – 14,99∙10^-3∙w (Al 2 O 3 ) -3476,07/T,                (7)

где χ – удельная электропроводность, См/см; КО – молярное криолитовое отношение; w(Al₂O₃) – содержание Al 2 O 3 , об. %; T – температура, К. Уравнение (7) действительно при 2,0≥КО≥1,2, в интервале изменения содержания дисперсного Al₂O₃ от 0 до 13 об. % в диапазоне температур от 1216 до 1018 К. Коэффициент множественной регрессии для этой зависимости равен 0,998.

Расхождение экспериментальных и рассчитанных по регрессионному уравнению (7) значений удельной электропроводности не превышает 3,7 %, среднее отклонение составляет 1 %.

Выводы

• 1.    Установлена линейная зависимость удельной электропроводности от содержания Al₂O₃ в криолитоглиноземных суспензиях. При увеличении содержания дисперсного Al 2 O 3 на 1 об. % удельная электропроводность в среднем снижается на 0,0215 См/см.

• 2.    Получено регрессионное уравнение, описывающее зависимость удельной электропроводности электролитов-суспензий системы Na₃AlF₆-AlF₃-5 мас. %. СаF₂-Al₂O₃ от КО, содержания глинозема и температуры (χ = f(КО, [Al 2 O 3 ], T)). Расхождение экспериментальных и рассчитанных по регрессионному уравнению (7) значений удельной электропроводности не превышает 3,7 %, среднее отклонение составляет 1 %.

Статья подготовлена и публикуется при поддержке Программы развития Сибирского федерального университета.