Электропроводность нанофрагментированного и модифицированного фуллереном алюминия

Исследования физических свойств новых наноматериалов явлются актуальными как с научной, так и с практической точки зрения, поскольку механизмы, определяющие их свойства, могут отличаться от обычных микрокристаллических материалов, что определяет и значительные отличия в свойствах [1].

Наноструктурирование позволяет управлять как механическими, так и транспортными свойствами материалов. Факторы, влияющие на механические свойства поликристалличе-ских металлов с нанометровым размером зерен, достаточно подробно исследованы [1-3]. В меньшей степени изучена, проблема, транспортных свойств наноструктурированных металлов [1].

Новые возможности для дальнейшего изменения свойств наноструктурированных материалов открываются при модификации границ между нанокристаллами в объемном материале. Так, в работе [4] были получены новые нанокомпозиты А1-С60 с образованием ковалентной связи между А1 и молекулами С60, исследованы механические свойства и предложена, модель структуры таких композитов. Для нанофрагментирования использовалась планетарная мельница. [5], эксперименты проводились с дюралюминием (93% А1) и А1 марки АДО (99,5%). Твердость образцов А1 с 3% С60 достигает 3 ГПа при размере кристаллитов А1 в спеченном образце около 50 нм. Такие значения твердости превосходят возможные значения как для наноструктурированного А1 без добавок [6], [2], так и для композитов А1 с многостенными углеродными нанотрубками [7], [8].

Таким образом, модификация межзеренных границ алюминия фуллереном позволила, существенно изменить механические свойства нанокомпозита по сравнению с нанострукту-рированным алюминием. Однако проблема, влияния такой модификации на. транспортные свойства композита А1-С60 остается открытой.

В данной работе проведено экспериментальное и модельное исследование влияния размеров кристаллитов А1 и концентрации С60 в нанокомпозите на его электропроводность. Построена, модель электропроводности композита, которая хорошо согласуется с экспериментальными данными и подтверждает предложенную ранее структуру нанокомпозита.

2.    Методика эксперимента

Электропроводность исходных материалов, использовавшихся в работе [2], была следующей: у алюминия АДО при 297 К она составляла 3, 3 • 107 Ом-1- м-1, а у дюралюминия существенно меньше. Поскольку отличие конечной твердости образцов из дюралюминия и алюминия АДО минимально, было выдвинуто предположение, что различий в образцах между сверхчистым и технически чистым алюминием также не будет заметно. Поэтому в данной работе было решено проводить исследования со сверхчистым алюминием марки A5N (99,999%), электропроводность которого при 298 К равна 3, 7 • 107 Ом-1- м-1 [9].

Тестовые образцы изготавливались следующим образом. В перчаточном боксе с атмосферой из чистого аргона и содержанием О2 и Н2О менее 0,1 ppm стружка из сверхчистого алюминия (A5N, 99,999%) смешивалась с гранулами С60 (99,5% чистоты). Массовая доля фуллерена в смеси составляла от 1 до 8%. После этого смесь укладывалась в барабан с внутренним диаметром 63 мм вместе со стальными шарами диаметром 9,5 мм общей массой 250 грамм. Барабан со смесью загружался в планетарную мельницу АГО-2, помол производился в течение 30-60 минут, частота вращения барабана составляла до 2220 об/мин.

Полученный порошок спекался в аргоновой атмосфере при давлении 2-6 кбар и температуре 250-280 °C в течение 15-20 минут. Далее полученная таблетка экструдировалась в проволоку диаметром 3 мм, при температуре до 290 °C и с усилием до 100 кН.

Электропроводность готовой проволоки исследовалась линейным четырехзондовым методом при комнатной температуре. В качестве источника тока использовался Keithley 4200 Source Meter, падение напряжения снималось с помощью Keithley 2182А.

Исследования рентгеновской дифракции проводились на спектрометре ARL X’TRA. Размер кристаллитов рассчитывался из дифракционной картины с помощью программы MAUD, которая среди прочего учитывает метод Вильямсона-Холла. Результаты, полученные таким образом, хорошо согласуются с изображениями, полученными методом темного поля на ПЭМ, в том случае, если размер кристаллитов меньше 100 нм.

Твердость образцов измерялась с помощью твердомера ПМТ 3 с помощью вдавливания пирамиды Виккерса при нагрузках 20-50 грамм.

Для того чтобы определить, как молекулы С60 распределены по объёму материала, проводились иследования методами просвечивающей электронной микроскопии (ПЭМ) и спектроскопии комбинационного рассеяния света (КРС).

Спектры КРС снимались с помощью спектрометра TRIAX 552 (Jobin Yvon), оснащенного CCD Spec-10, 2KBUV (2048 512) (Princeton Instruments). Длина волны света возбуждающего лазера составляла 514,5 нм, разрешение — 1 см-1.

3.    Результаты эксперимента3.1.    Исследования свойств

Было создано несколько серий образцов.

В первой серии опытов выявлено влияние параметров спекания и компактирования образца на его электропроводность и твердость. Три образца были скомпактированы из последовательно приготовленных порошков с массовой долей фуллерена 1%, временем помола 30 минут; первый — холодным прессованием при нагрузке 3 кбар, следующие два — горячим прессованием при температурах отжига 190 °C и 250 °C и нагрузках 3 и 4 кбар. Как и следовало ожидать, при холодном прессовании рекристаллизация происходит слабее и размер кристаллита меньше. При этом электропроводность наибольшая у хорошо отожжённого образца, а твердость — у спрессованного вхолодную.

Во второй серии опытов изучалось влияние массовой доли фуллерена на параметры

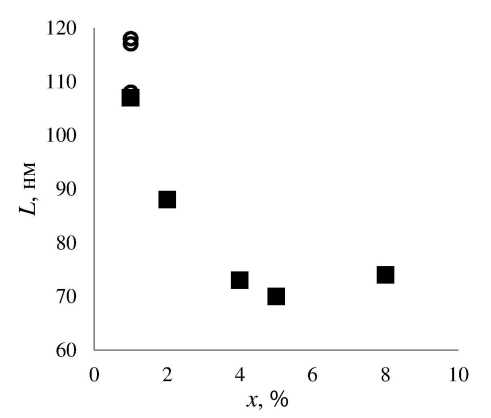
Рис. 1. Зависимость среднего размера кристаллита (L) в экструдированном образце от массовой доли С60 (ж) для двух серий образцов: образцы первой серии обозначены кругами, второй серии — квадратами

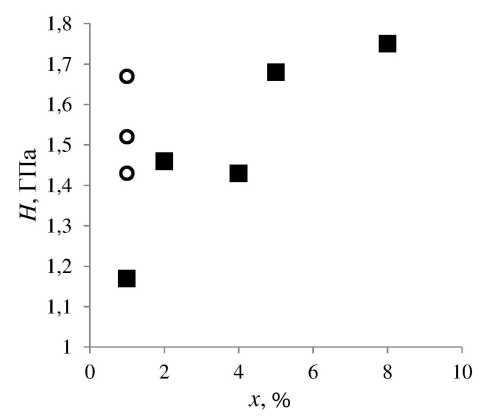
Рис. 2. Зависимость твердости экструдированной проволоки (Я) от массовой доли С60 (ж) для двух серий образцов: образцы первой серии обозначены кругами, второй серии — квадратами

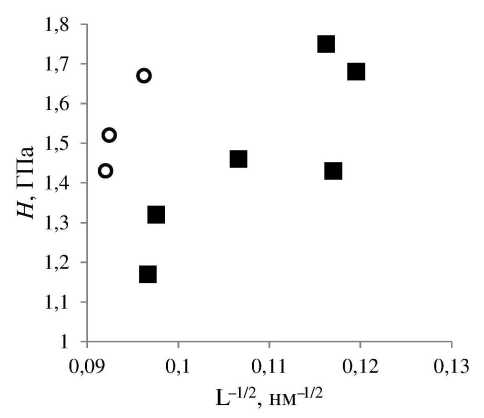
Рис. 3. Зависимость твердости экструдированной проволоки (Я) от среднего размера кристаллита (L) для двух серий образцов: образцы первой серии обозначены кругами, второй серии — квадратами

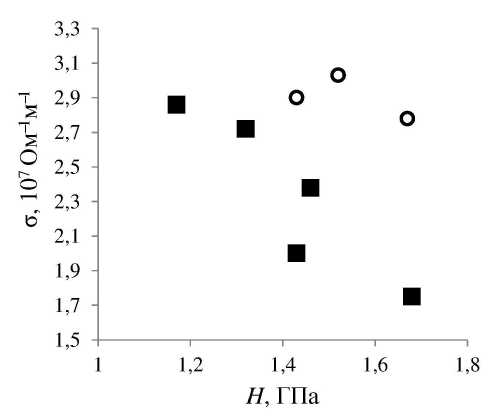
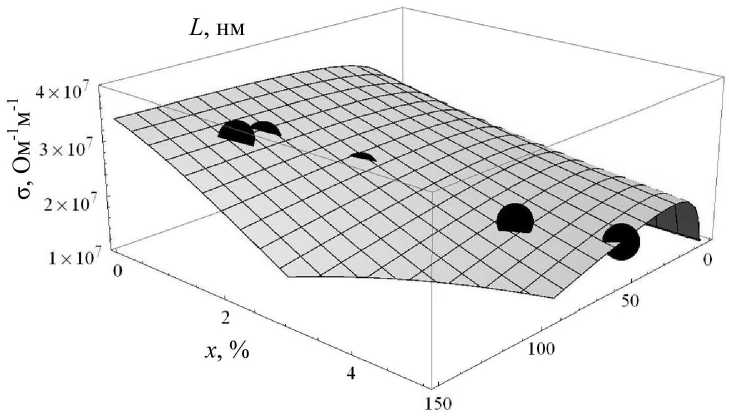
Рис. 4. Электропроводность ст и твердость Н для двух серий образцов: образцы первой серии

обозначены кругами, второй серии — квадратами полученных образцов. Были получены проволоки с 1, 2, 4, 5 и 8 вес.% фуллерена (помол 30 минут).

Результаты измерения свойств образцов второй серии опытов приведены на рис. 1, 2, 3 и 4.

Твердость образцов достигает значения 1,75 ГПа (более чем в 10 раз превосходит значение 137 МПа для особо чистого алюминия [10]), а электропроводность — (более 80% от исходного).

Следует также отметить, что образцы первой серии имеют размер кристаллитов, превосходящий 100 нм, поэтому для них сложно делать утверждения о правильности данных значений.

Измеренная плотность образцов составила 2,675 г/см3 для образца с 1% С60 и 2,655 г/см3 для 4 вес.% Сео. Учитывая количество молекул С60, их массу и размер[11], можно получить теоретические значения для плотности этих образцов: 2,695 и 2,681 г/см3 соответственно, т.е. возможная пористость образцов меньше 1%.

3.2.    Исследования структуры

Электронная микроскопия или сканирующая зондовая микроскопия пока не позволили разрешить отдельные молекулы фуллерена, находящиеся на поверхности алюминиевых кристаллитов. Изображения просвечивающей электронной микроскопии, на которых действительно можно установить наличие некоего аморфного углеродного слоя на поверхности алюминиевых кристаллитов перпендикулярно этому слою, были сделаны только для образцов с большим количеством Сео и малым временем обработки, где слой фуллерена получается достаточно толстым [2].

Когда слой становится более тонким, увидеть его в электронный микроскоп не удалось, что иллюстрирует рис. 5. Однако удалось получить изображение этого слоя, снятое параллельно границе зерен (рис. 6) — на нём виден некий углеродный материал. Наличие именно Сео показывают данные спектроскопии комбинационного рассеяния света, снятые с этого же места.

Поэтому основным методом, позволяющим установить наличие фуллерена Сео в образцах, является спектроскопия КРС.

На рис. 7 приведены типичные спектры КРС для образца с 5% Сео (сверху) и образца с 1% Сео (снизу) для длины волны возбуждения 514,5 нм. Как показано в работе [2], эти спектры имеют вид, характерный для аморфного Сео, когда молекула фуллерена возмущена внешними ковалентными связями.

Рис. 5. ПЭМ-изображение границы зерен (граница перпендикулярна плоскости рисунка)

Рис. 6. ПЭМ-изображение слоя С60 на границе зерен (граница параллельна плоскости рисунка)

С помощью этих спектров также можно ответить на вопрос о сохранении фуллерена в образцах и об отсутствии в них карбида алюминия. Для этого их нужно сравнить со спектрами карбидизированных образцов на рис. 8. Верхний спектр на рис. 8 соответствует нанокристаллическим зародышам Al4С3 (менее 2 нм), которые образуются, если в нагретых до 330 °C фуллереносодержащих образцах только начинается карбидизация. При более длительном нагреве или с ростом температуры и давления [2] происходит транспорт углерода к зародышам карбида, образуются более крупные кристаллиты карбида и их спектр уже выглядит так, как на нижнем спектре на рис. 8. Характерные для нижнего спектра пики, а также плато для среднего в исследуемых образцах не наблюдаются. Таким образом, по спектрам КРС в исследуемых образцах отсутствуют следы карбидообразования.

4.    Обсуждение результатов

В работе [2] было показано, что молекулы фуллерена располагаются по границам алюминиевых кристаллитов (оболочечная модель). Находясь на границах кристаллитов, фуллерен препятствует процессам рекристаллизации. Это приводит к уменьшению минимального размера кристаллита, получаемого в результате помола в заданных условиях, а также ослабляет рост кристаллитов при компактировании образцов.

При работе в области размеров кристаллитов, больших критического (для закона Холла-Петча), эффект подавления рекристаллизации создаёт дополнительное упрочнение за счет закона Холла-Петча [12]. Так, при компактировании А1 порошка без добавок С60 при температуре выше температуры рекристаллизации размер кристаллита может значи-

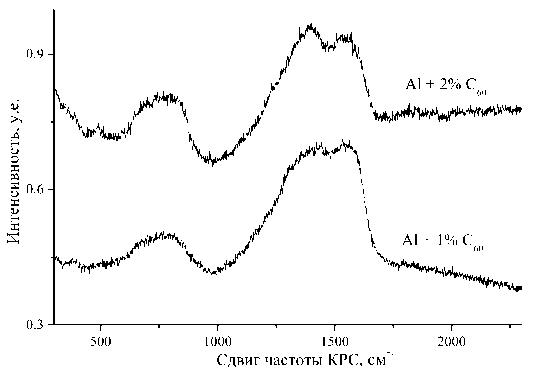
Рис. 7. Спектры КРС для образцов с 2% и с 1% С60

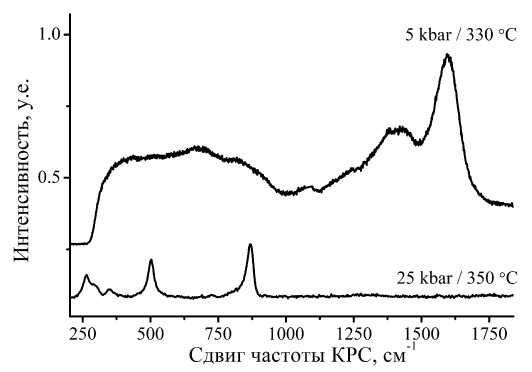
Рис. 8. Спектры КРС-карбидизированных образцов

тельно вырасти [6]. При работе с меньшими размерами кристаллитов предполагается появление других механизмов упрочнения, например, связанных с подавлением межзеренного проскальзывания из-за наличия фуллерена на границах.

Рассмотрим влияние на электропроводность материала (в данном случае — алюминия) двух факторов: наноструктурирования и модификации поверхности зерен фуллереном. Сначала рассмотрим влияние только наноструктурирования (т.е. наличия в материале большого количества границ), а потом учтем модификацию этих границ наличием фуллерена.

4.1.    Модель Маядаса—Шатцкеса

Влияние первого фактора можно описать известной моделью Маядаса-Шатцкеса для поликристаллических металлических тонких пленок [13], в которой рассматривается решение уравнения Больцмана для непрерывной среды, разделенной потенциальными 5 - образными барьерами, расстояния между которыми совпадают с размером зерен в материале. В этой модели

^Grain — &Bulk • 3

- ^а + а² - а³ ln(1 + 1)) , 2                 а /

а =

^MeanBulk R

L 1 - R’

где CTGr_ai_n ~ электропроводность пленки, учитывающая рассеяние на. границах 'зерен. <7B_uik — электропроводность исходного объёмного материала, ^M_eanB_uik ~ длина свободного пробега в исходном металле, обусловленная рассеянием на фононах и дефектах решетки, L — размер зерна, R — коэффициент отражения электрона от одиночного С-образного барьера. Коэффициент R является эмпирическим параметром в этой модели, в работе [14] Маядас и Шатцкес получили для поликристаллических пленок алюминия значение R = 0,15. Другими авторами также были получены R = 0,19 [15] и R = 0,23 [16].

4.2.    Учёт наличия фуллерена

В рамках модели Маядаса-Шатцкеса можно ввести эффективный (средний по всему образцу) коэффициент отражения от границы:

^Reff = к free ^{1 R}free + ^кС₆ о • ^ДС бо ’

где kf_ree — доля чист ой границы, kc₆₀ = 1 — kf_ree — доля заполненной фуллереном границы. Rf_ree — коэффициент отражения электронов от чистой грашшы. Rc₆₀ ~ от полностью заполненной фуллереном границы.

Задача о электропроводности сводится к нахождению вида зависимости kf_ree от различных параметров образца (отношение массы С60 к массе А1 ж = Мс₆₀/Мді и средний размер кристаллита L).

В работе [17] методом функционала плотности был проведен расчет проводимости единичной молекулы С60, заключенной между двумя плоскостями из алюминия. Полученное в ней значение для проводимости

6е2

G Һ где е - заряд электрона, Һ — постоянная Планка. Зная размеры молекулы фуллерена

(dc₆₀ ~ 1 нм=< [11]), пересчитаем её в некую эффективную удельную проводимость в

этой точке по формуле

G •d

^60

4^d3

3    60

= 2, 9 • 105 С)м-1

м

Удельная электропроводность исходного объёмного алюминия - величина порядка

• 3,    5 • 107 С)м^-1 •м 1, что на два порядка больше значения (3). Тогда в первом приближении значение Rc₆₀ ~ 0, 99 ~ 1-

• Также введем фактор формы я как отношение площади всех границ S внутри единичного объёма материала V к объёму V:

S г v = L’

где L — размер кристаллита. Для беспористого материала отношение (4) ровно в два раза меньше, чем отношение площади поверхности к объёму фигур, задающих форму кристаллитов. Для модели материала, составленного из кубических кристаллитов, г = 3 3/ 6/л та 3, 72, для абсолютно соприкасающихся шаров я = 3. Скорее всего, истинное я лежит между этими двумя значениями, например его можно взять равным 3,4. При необходимости в дальнейшем его можно уточнить с помощью исследования изображений, полученных методом темного поля на ПЭМ.

Наиболее простое предположение о kf_ree заключается в том, что фуллерен располагается по границе равномерно до тех пор, пока не заполнит её монослоем при kf_ree = 1.

Пренебрегая отличием в плотности алюминия на границе, для такой модели довольно просто получить выражение

^С бо — 1    kfree — ^

^fco ) ² P az xN _a 12цсбо + 2^(^Сбо )³ $РА1 N a ’

где p ai — плотность алюминия, р_с 60 ~ молярная масса Сбо, N a — число Авогадро.

Поскольку 0 6 кд₆₀ 6 1, область применения такой модели выглядит следующим образом (рис. 9).

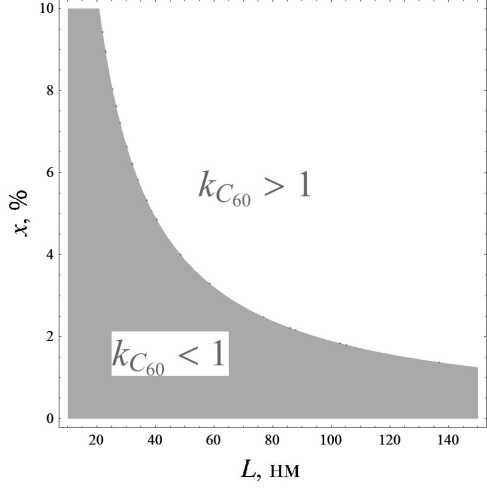
Рис. 9. Область применения модели равномерно распределенного фуллерена

При kj_ree ^ 0 и Rc₆₀ ~ 1 электропроводность материала должна сильно упасть (например, до значения 1, 3•Ю⁵ Ом^-1 • м^-1 при L — 75 нм и Rc₆₀ — 0,99), и по вышеприведенной модели это должно произойти с образцом, содержащим 4% С6ц. Однако эксперимент показывает, что его электропроводность равна 2 • 107 Ом^-1 • м^-1, т.е. падение не такое значительное.

Скорее всего, это означает, что распределение фуллерена на поверхности не является равномерным и при больших х и L нужно использовать более сложную модель. Ввиду сложности процессов, происходящих в мельнице, точное теоретическое описание не представляется возможным, поэтому используем следующее серьёзное модельное упрощение: предположим, что все молекулы располагаются на поверхности случайным образом по-очереди и независимо друг от друга.

Возьмем всю площадь поверхностей в образце. Пусть количество молекул С60, которое можно на ней поместить монослоем, равно С. Тогда задача формулируется так: нужно случайно разместить N элементов по С клеткам. Вероятность помещения элемента в конкретную клетку равна р — С ^ 1- Тогда этот процесс является последовательностью испытаний Бернулли с вероятностью успеха р и количеством испытаний N. С учётом того, что N ^ 1, р ^ 1, вероятность того, что в клетке окажется т элементов при среднем количестве элементов на клетку mA_verage, дается распределением Пуассона:

P(m) — A

ГДС А — Np — § = т Average.

Среднее количество молекул на клетку выразим через массовую долю С60 х:

х = М⁶⁰

^N • ^тСбо ,

Mai    pai • VAz

;

Pai Vai Na

N —---------• ж.

РСбо

Здесь Мс₆₀ — полная масса фуллерена в образце, Mai - масса алюминия, VAz — объем алюминия, шс₆₀ — масса одной молекулы Сбо.

Предположим, что на поверхности кристаллитов фуллерены образуют плотную упаковку с плотностью £ = 2^23 ~ 0, 9069. Тогда.

_ N ^ Average — С

С — ^N

^Sc60

Р aiVaiN a ^Сбо ^{z C}X

^S °^С60

zV_s E—^. S ;

^Sc60

Pai ^Na ^Sc_№^Vai

VL;

v v        Мсбо  Mai

Ve — Vc6o + Vai ~--1--

Pai     Pai

—M_At (ж + 1) — Vai (1 + ж); Pai

_ PaiNaSc6o

^Average,

РС60 SZ1 + ж

Используются обозначения Se — общая площадь поверхности границ в образце, Ve — объем образца, Sc₆₀ — площадь поверхности границ, занятых фуллереном.

Тогда доля свободной поверхности равна kjree = P(0) — е А — е mA'^-.

4.3.    Сравнение модели с экспериментом

С использованием изложенной выше модели (7) построена трехмерная поверхность в координатах «электропроводность — размер кристаллита — массовая доля фуллерена». На этом же графике изображены точки, соответствующие экспериментальным образцам, причем вместо трех точек серии «А» изображена одна точка, т.к. в этих координатах они сливаются. На рис. 10 изображена проекция этого трехмерного графика. Поверхность, построенная по теоретической модели, построена со следующими параметрами: Rai — 0,15; z — 3,4; Rc₆₀ — 1; ^с₆₀ — 0.9 нм. Параметры выбирались для наилучшего соответствия теории с экспериментом.

Рис. 10. Произвольная проекция трехмерного графика зависимости электропроводности а от массовой доли С60 х и среднего размера, кристаллита. L

Хорошее соответствие с экспериментом и правильное качественное поведение поверхности, обусловленное частью модели, ответственной за учёт наличия фуллерена, является дополнительным подтверждением предполагаемой оболочечной модели структуры композита.

5.    Выводы

Предложена модель, описывающая электропроводность нанофрагментированного и модифицированного фуллереном алюминия.

Получены и исследованы образцы с различными массовыми долями Сбо и размерами кристаллитов, проведены измерения среднего размера кристаллитов, электропроводности и твердости этих образцов. Проведено сравнение теоретической модели с экспериментальными данными. Модель хорошо согласуется с экспериментом, что подтверждает верность оболочечной модели стуктуры материала.

Показано, что твердость алюминия может быть повышена более чем в 10 раз при сохранении электропроводности на уровне 0,80 от значения исходного (поликристаллического) сверхчистого алюминия.

Исследования структуры материала методами спектроскопии КРС показывают наличие ковалентных связей между алюминием и молекулами Сбо и согласуются с предложенной оболочечной моделью.

6.    Благодарности

Работа проводилась при финансовой поддержке Министерства образования и науки Российской федерации ГК № 16.552.11.7014, ГК № 16.523.11.3002 и ГК № 02.740.11.0792.