Электростатические планарные ионные Z 2-ловушки

В статье изложена теория электростатических ионных ловушек с идеальной пространственно-временнóй фокусировкой ионного пакета вдоль одной из координат, временнóй фокусировкой по другой координате и удержанием по третьей.

Кл. сл. : электростатическая ионная ловушка, масс-спектрометрия

БЕЗРАЗМЕРНАЯ МОДЕЛЬ ИОННО-ОПТИЧЕСКОЙ СИСТЕМЫ

Теорию масс-спектрометров наиболее удобно изучать при помощи безразмерной математической модели, содержащей минимальное число символов. Введем в качестве линейного масштаба какую-либо характерную длину реальной системы £ , например ее габарит, а единицу времени T выберем таким образом, чтобы из функции Лагранжа L выделился единый постоянный множитель, который в уравнениях Лагранжа сокращается. Физические координаты X , Y , Z и время t свяжем с безразмерными параметрами x , y , z , τ соотношениями:

X = £ • x , Y = £ • y , Z = £ • z , t = T • т.      (1)

Потенциал электростатического поля

Ф = Ф о • Ф(x , У , z ),                (2)

где Ф 0 — характерное значение потенциала, выбранное из каких-либо физических или инженерных соображений, а ϕ ( x , y , z ) — безразмерный потенциал, удовлетворяющий уравнению Лапласа

Ф хх + Ф уу + Ф zz = 0.                ⁽³⁾

Единицу времени T определим формулой

T = £ • Jm/\q Фо| ,               (4)

где q и m — заряд и масса иона.

В этих условиях унифицированная функция Лагранжа иона в безразмерных переменных примет вид

L = 2 • ( X ² + У 2 + Z¹ ) - Ф ( x , У , z ).      (5)

Точки над символами обозначают дифференциро-

вание по безразмерному времени τ . Уравнения движения могут быть записаны в виде

x = - Ф х ,

У = - Ф у , z = - Ф z ,

где нижние символы обозначают соответствующие компоненты переменных. Физические начальные данные движения

X I , = 0 = X 0 , Y t = 0 = Y o -    Z t = 0 = Z 0

d X _ V d Y d t t _ ₀      x , d t

= V y ,

d Z d t

= Vz t=0

при переходе к безразмерным переменным преобразуются в

x 0 = X 0 /£ ,    y 0 = Y 0 /£ ,     z 0 = Z 0 /£ ,

X o = TV x /£ , У о = TV y /£ , z o = TV z /£ .    °

Вместо начальной кинетической энергии

E_n = —mV ², где V =,/ V _r ² + V + V ² , появляется 0 2      0             0         x y z

безразмерный параметр w = ^- (, x 2 + У 2 + z 2 ) , имеющий весьма ясный физический смысл. Если воспользоваться единицей времени, определенной выражением (4), w может быть записан как

w = E о/ q ^Ф о|.

Иначе говоря, безразмерная кинетическая энергия w выражает реальную кинетическую энергию E ₀ в долях характерной потенциальной энергии | q Ф ₀1 иона в данном поле. Если далее выразить x₀, У ₀, z ₀ через w , то становится очевидным, что весь набор безразмерных начальных данных (7) не

зависит от массы иона, но только от его энергии старта E ₀ . Это означает, что любой пакет ионов разной массы, но одинаковой энергии можно рассматривать как своеобразную абстрактную обезличенную частицу, для которой вся динамика и кинематика определяется только параметрами (7) и структурой безразмерного потенциала ϕ ( x , y , z ) .

ПРИНЦИП ИДЕАЛЬНОЙ ПРОСТРАНСТВЕННО-ВРЕМЕННÓЙ

ФОКУСИРОВКИ

Сконструируем класс лапласовых потенциалов вида

Ф = f (x, y) + az 2-(9)

Подставляя ϕ ( x , y , z ) в уравнение Лапласа (3), получим двумерное уравнение Пуассона для функции f ( x , y ) :

fx + fy + 2 a = 0,(10)

а уравнения движения (6) примут следующий вид:

x = - fx(x, y), y = - fy (x, y),(11)

z = - 2 az .

Очевидно, движение вдоль оси z отделено от движения в плоскости xy и связано с ним только посредством начальных данных.

Если a > 0, то третье уравнение системы (11) — уравнение колебаний, и движение вдоль z немедленно находится в виде z„ z = z0 cos (V2a т) + ^- sin (V2a т).     (12)

Пусть в момент старта пакет частиц, распределенный по скоростям x0, y0, z0, имел вид плоскости z = z0. Тогда из формулы (12) легко заметить, что в моменты тп = пи)22а, n = 1,2,3,...        (13)

функция z перестает зависеть от z0, поскольку sin (пи) = 0, а координата zn принимает значения zn =(-1)nz0, и = 1,2,3,...         (14)

Иначе говоря, лист снова стал бесконечно тонким, несмотря на разброс частиц по скорости z 0 . Физическое время полета и координата получатся при помощи T , t :

t = T • т nn

= £ пи

m

\² a\q ^ф 0,,

Z n = t • z n = ( - 1 ) ⁿZ 0 , и = 1,2,3,....

Это важное для масс-спектрометрии явление можно назвать принципом идеальной пространст-венно-временнóй фокусировки. Как видно из (15), ионы каждой массы проходят плоскости фокусировки Z = ± Z ₀ в разные моменты времени t_n и, следовательно, они уже диспергированы по времени пролета пропорционально m . За несколько циклов этого колебательного процесса можно накопить большую дисперсию. Данный эффект, по-видимому, впервые описан в патенте [1].

Можно сказать, что квадратичная часть потенциальной энергии воплощает идею идеального масс-рефлектрона с полной компенсацией энергетического разброса в ионном пакете. Если реальный пакет имеет вид таблетки толщины d вдоль оси z и проекцию на плоскость xy в виде небольшого пятна, то с течением времени это пятно расплывется и займет область достаточно больших размеров, если только силы электрического поля не помешают этой деформации пакета. Заметим также, что, согласно (12), указанная идеальная пространственно-временнáя фокусировка (в плоскости z = 0) осуществляется и в том случае, когда ионы стартуют одновременно с различными начальными координатами z ₀ Ф 0 и нулевой начальной скоростью z ₀. В этом случае, реализуемом при ортогональном оси z вводе пучка, уширение пакета в плоскости z = 0 обусловлено ненулевыми начальными z -скоростями и сохраняется постоянным в течение всего времени масс-анализа.

Таким образом, инжектируемый в поле анализатора ионный пакет должен в идеале иметь либо нулевую протяженность по направлению идеальной фокусировки (при произвольном разбросе по скоростям), либо нулевую скорость z ₀ при произвольном разбросе по координате z в момент старта. Детектирование диспергированных по времени пакетов (соответствующих различным массам) возможно либо непосредственно, с фиксацией времени пролета, либо путем анализа наведенного тока на сигнальном электроде, размещенном в плоскости идеальной пространственно-временнóй фокусировки пучка. В последнем случае возникает необходимость анализа спектра колебаний наведенного тока с учетом того, что частота, соответствующая колебанию ионного пакета массы m , определяется соотношением

2 п   2V² a I q ^ф01

<У„ =---= —2------ t1         l m

.

При конструировании ионно-оптических сред мы должны в первую очередь выработать правила выбора функции f ( x , y ) , гарантирующей нужную структуру сил, при которых ионный пакет удерживается в заданных размерах по направлениям x , y .

ПЛАНАРНЫЕ ЛОВУШКИ

Представим потенциал (1) в виде ф = p(x,y) +(z2 -y2).          (17)

Это — суперпозиция двух сугубо двумерных полей — квадруполя z ² - y ² и поля с потенциалом p ( x , y ) . Характерно, что квадруполь не вносит компоненты силы вдоль оси x и, значит, она определяется только структурой потенциала p ( x , y ) . Это обстоятельство оказывается очень ценным при синтезе класса ионно-оптических сред. Чтобы перейти к такому синтезу, мы рассмотрим множество гармонических функций p ( x , y ) , симметричных по y относительно оси x :

Р(x, У) = P(x,- У).(18)

Ход потенциала вдоль оси x p | y=o = u(x)

однозначно определяет потенциал в окрестности оси (при y * 0) в виде ряда

. . u "( x ) ₂ H IV ( x ) ₄

P = u (x)--y 2 + 24 y4 +...,(20)

который легко вычисляется из уравнения Лапласа методом неопределенных коэффициентов.

Данный ряд — классическое средство представления потенциалов в традиционной электронной оптике параксиальных пучков, и он хорош именно для динамических исследований заранее выбранных полевых структур прямым способом анализа.

Однако в задаче синтеза, когда искомым является потенциал и электродная конфигурация, его реализующая, этот ряд ввиду ухудшения сходимости с ростом | y | теряет свою привлекательность. Здесь более выгодно воспользоваться формулой комплексного потенциала для симметричных двумерных полей, которая непосредственно дает выражение его через функцию u ( x ) .

Итак, положим

Q ( x , y ) = s ( x , y ) + i p ( x , y )

и

Q ( x + i y ) = i u ( x + i y ), p ( x , y ) = Im Q ( x + i y ).

Это выражение вполне очевидно и не требует дополнительных комментариев. Преимущество его перед представлением (20) в том, что оно охватывает глобальную картину поля вместе с особенностями, где бы они ни находились, в отличие от ряда (20), действующего вполне эффективно только в очень узкой полосе | y | < 5 и, следовательно, не отражающего истинную геометрию эк-випотенциалей вдали от оси симметрии x .

Далее займемся непосредственным синтезом одномерного потенциала u ( x ) , удовлетворяющего условиям пространственно-временнóй фокусировки (уже не идеальной) ионного пакета по координате x и удержания ионов по координате y . Удобно использовать для этой цели квадратичные по x функции.

Рассмотрим зеркало с ходом потенциала вида u (x) = A (1 - (1 - x / b )2). (22)

Время возврата τ ₁ частицы в точку 0 при старте из нее же с энергией w дается интегралом

xr

τ ₁

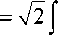
d x

V A (1 - x / b )² - ( A - w )

b

2 A

ln

A + +

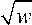
A

-

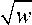
Далее рассмотрим линзу с параболическим ходом потенциала

u ( x ) = B (1 - x ²/ h ²).             (24)

Время пролета сквозь линзу по оси x от - h до + h дается интегралом

1 h         dx т 2 = -/=   /

V2 -h^ w - B (1 - x ²/ h ²)

h

2 B

, w+ + BB ln              .

Ч w - Bb

Время пролета по дрейфовому отрезку H дается формулой

H т 3 =15;:

2 w

.

Из всех этих элементов составим потенциальный рельеф вида, как показано на рис. 1.

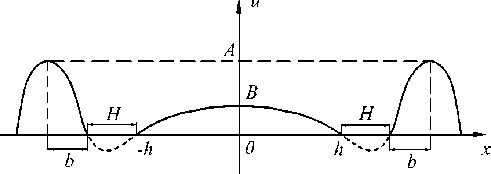
Рис. 1. Потенциальный рельеф системы

А т*

( A w )²

2w w ^3/2( + - w )

r_ hw

V

+ - B

( w - B )²

₊ H + I + H — I.

w )

Отрезки H , соответствующие переходным областям, должны быть малыми на фоне b и h . Следовательно, для оценок имеет смысл положить H = 0 и выразить b из (31). Тогда

*

т =

= 2h h

1 + - w

Если B <  w <  + , то ион колеблется в этой сложной яме с периодом τ ^*

_v xT+ w - B

ln

+ + + ww

A

-

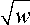
1 , w+ + Bb

+-/=ln-r— r= BB Bw - b b J

, (34)

Т = 2 т 1 + 2 т ₂ + 4 т 3 ,             (27)

A r' = h _Г+:ВМ_ .

V 2 w ( + - w )( w - B )²

или

*

т =

г- b . ++ + V w

2 ln

( V +  + - - V w

h . V w + BB

+ -/=1П”г=---/=

V b  ww - Bb

2 H I '

V w )

d τ ^*

Высчитаем и приравняем нулю. Получим: d w

— = Е f— bhH ) = 0.  (29)

d w  V w v + - w w - B w )

Это — условие фокусировки первого порядка d2τ по энергии. Далее вычислим 2 :

d w ²

d² τ ^* d w ²

1 Г b (3 w - + ) + V2 w ^3/2 V ( + - w )²

h (3 w - B ) + 3 H I ₍₃₀₎

( w - B )²    w ) ¹

Если выразить b из (29)

+-w   +-w b = h----+ H---- w - B w

и далее вставить его в (30), то получим выражение d² τ ^*

для в условиях фокусировки первого поряд-d w ²

ка по энергии:

d² т * = V2

d w ²    w ^3/2 ( + - w )

hw

+ - B

( w - B )²

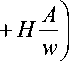
Таким образом, фокусировка второго порядка в данной системе не достигается ни при каких значениях параметров, т. к. выражение (32) никогда не обращается в нуль. Приращение периода А т * при вариации энергии A w в этих условиях запишется формулой

А т*

Отношение _* не зависит от h в условиях τ ^*

фокусировки и определяется только соотношением энергий и потенциалов.

Поперечная фокусировка

Восстановим пространственное распределение потенциала, отвечающее распределениям u ( x ) из (22) и (24):

Ф1 = z ² + + ( 1 - ( x / b - 1) 2 ) + ( + / b ² - 1 ) y ²,      (36)

Ф2 = z ² + B ( 1 - x ²/ h ² ) + ( B / h ² - 1 ) y 2 .         (37)

Если + / b ² >  1 и B / h ² >  1, то коэффициенты при y ² положительны и, следовательно, силы по y как в зеркалах, так и в линзе исключительно фокусирующие. Более того, благодаря полному разделению переменных, времяпролетные свойства этих элементов вдоль оси x не зависят от смещения y . И хотя качество энергетической фокусировки здесь отнюдь не рекордное, данная схема может дать ловушку с очень большим фазовым объемом потока. Легко понять, что реальные полеза-

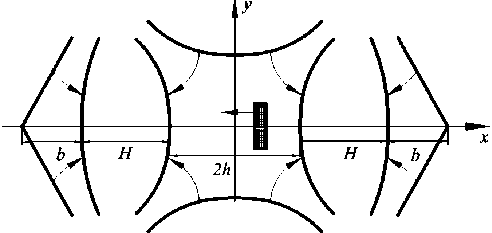
Рис. 2. Полезадающие электроды элементов ловушки

дающие электроды этих фокусирующих систем представляют собой гиперболоиды.

При такой геометрии весьма сложно совместить эти элементы так, чтобы зазоры H исчезли. Они остаются, и на их месте возникает рассеивающее поле от некомпенсированного члена - у ² в потенциале. Если в эти места встроить рассеивающие линзы, то рельеф на рис. 2 можно сделать приемлемо гладким. Однако и в таком разрывном виде система выглядит в техническом смысле весьма привлекательной, поскольку поверхности второго порядка легко реализуются в металле. При A = 2, например, конус зеркала круговой, как и гиперболоиды-чашки. Но линза в силу условия B <  A уже представляет собой сплющенный гиперболоид.

Схему подобного рода можно создать из любых фокусирующих зеркал и линз, и у всех у них будет один общий дефект — переходная рассеивающая область, которую, однако, можно сделать достаточно узкой. Качество временнóй фокусировки, безусловно, можно повысить за счет специального подбора неоднородности зеркала, но при этом может быть утрачена устойчивость по y , обеспечивающая большой фазовый объем пакета и равномерность фокусировки по всей площади пакета. Кроме того, наличие щелей в электродах зеркал и линзы вносит еще один сложно учитываемый фактор в виде дополнительных линз. Чтобы сделать электронно-оптический тракт сквозным, описываемым единым аналитическим выражением, использован математический прием аналитической сшивки (соединения) элементов с различными потенциалами.

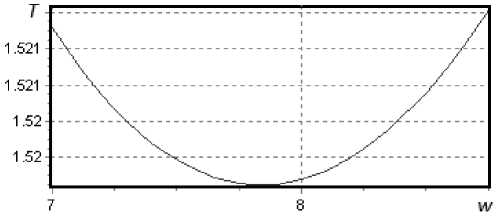
Рис. 3. Полупериод x -колебаний в ловушке

Пример 1

В предложенной системе удается обеспечить удержание пакета ионов по у с одновременной энергетической фокусировкой первого порядка по x при наличии идеальной пространственно-временнóй фокусировки по z .

Поле электростатической ловушки задается выражением [2]

ф(x , у , z ) = z ² - kx ² - (1 - k ) у ² +

⁺ E ^A i Ф o^{( x} - x , У , a i , b i , c i )         (38)

i = 0

где

Ф ₀( x , у , a , b , c ) = 2 xy • s ₁ + ( x ² - у ² + c ) • s ₂,

=            sin 2 ау

• ¹    2(cos2 ау + cosh 2 a ( x - b )/

_s = 1 +       sinh 2 a ( x - b )

• ²  2 2(cos2 ау + cosh 2 a ( x - b ))

  

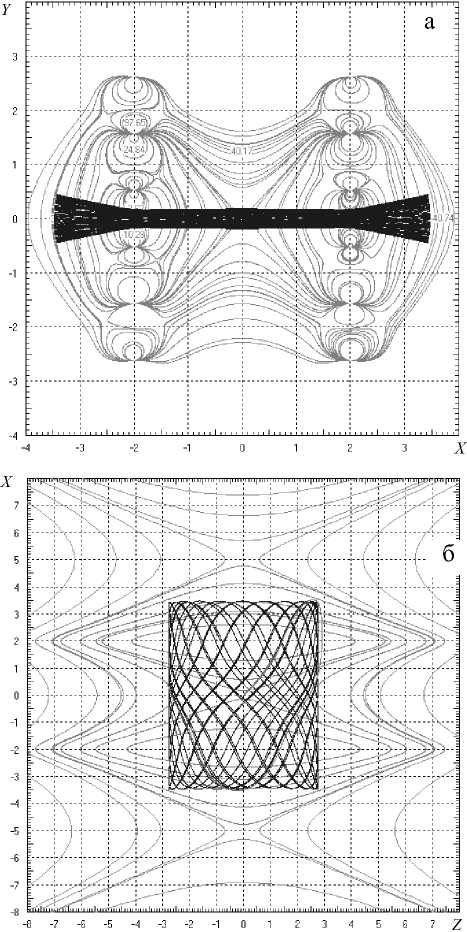
  Рис. 4. Проекции траекторий ионов на плоскости XOY (а) и ZOX (б) на фоне эквипотенциалей поля ловушки

  
  

Зависимость полупериода x-колебаний в ловушке от энергии имеет минимум, что говорит о наличии x-фокусировки по энергии (рис. 3). Качество работы системы позволяет оценить рис. 4.

а

б

г

в

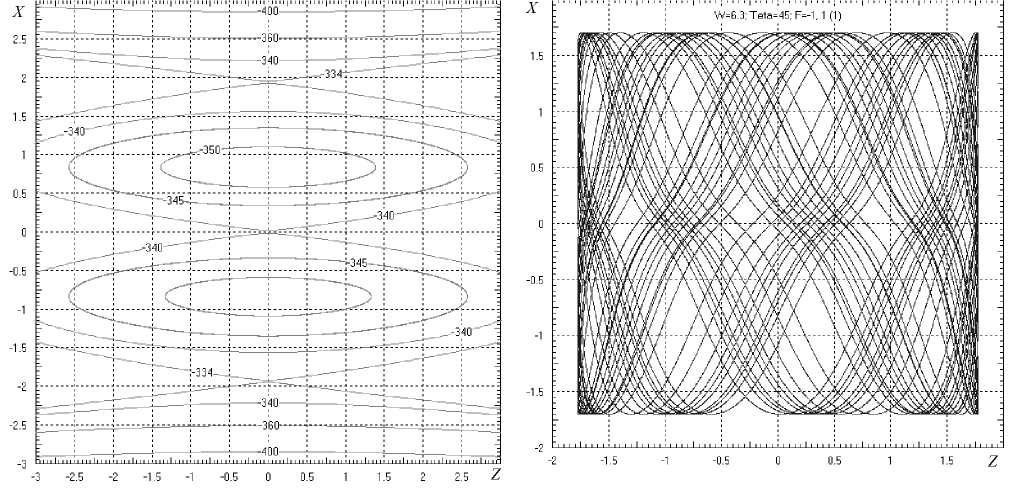
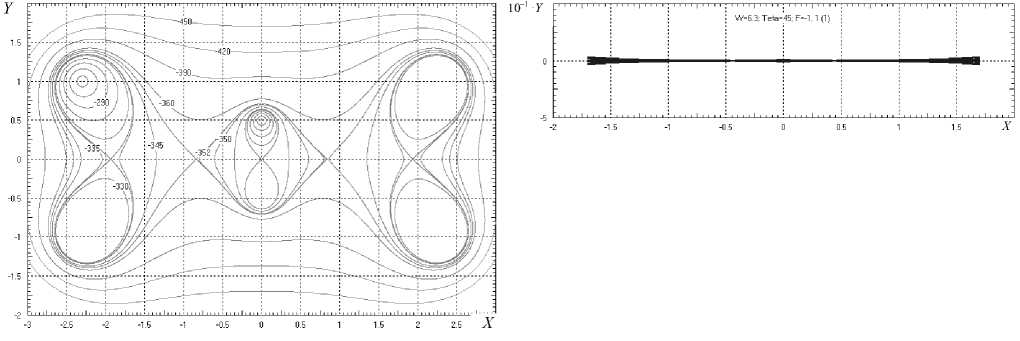
Рис. 5. Альтернативная полевая конфигурация: а, в — сечения эквипотенциальных поверхностей плоскостями Z = 0 и Y = 0 соответственно; б, г — траектории в проекции на плоскости Z = 0 и Y = 0

Пример 2

Рассмотренная в Примере 1 полевая структура может быть существенно упрощена при качественном сохранении динамики пакета. Альтернативная полевая конфигурация, содержащая логарифмические функции, проиллюстрирована рис. 5.