Электроупругость пористых пьезокомпозитов

The actual problems of mechanics, which requiring the special studies, pertains a special studies of characteristics of new composite (smart) materials, capable by itself to change their own characteristics and geometry due to the introduction to the composite structure the active operated elements from piezoceramic. Purpose of the work is concluded in the development of principles of design and development scientific bases of mathematical theory of deforming piezoactive composite materials, study of the influence of stochastic particularities of technology of real structures on the effective physical and mechanical characteristics of piezocomposites. Achievement of this purposes is expected to realize (by structured-phenomenological approach) on the base of development of new and (generalising on the class of piezoactive composites) known methods of mechanics of composite materials for deciding the boundary-value problems of statics and dinamics of inhomogenious medias. The structure of considered composite material have statistical homogeneity, quasiperiodicity or, in the limiting case, periodicity.

Постановка задачи

Модели квазипериодических структур основаны на внесении в идеальную периодическую структуру композита той или иной разупорядоченности. Рассмотрим более подробно двухфазные квази периодические модели, когда форма и размер однородных включений детерминированы, а их случайные положения могут быть заданы вероятностным законом только для вектора а случайных отклонений центров от узлов известной периодической решетки [1-4]. Считаем, что включения не могут выйти за границы своих ячеек. Расположение периодической решетки относительно координатных осей г₍ случайно. Решетка имеет независимые случайные смещения Z, с равномерными законами распределения на соответствующих отрезках [0, f ], где 7] - периоды решетки по координатным осям ^ , i = 1,2,3. Это позволяет предположить наличие свойств статистической однородности и эргодичности как у квазипериодической, так и у соответствующей периодической структуры.

В представительной области квазипериодического композита V с границей Г рассмотрим решение стохастической связанной краевой задачи электроупругости h™(r>„,n(r)]v +ky(r)

М/|Г=ЕУ ’

<Р|г=-£/у

относительно полей перемещений u(r) и потенциала электрического поля ср(г), где в* и Е - заданные тензор однородной макро деформации и вектор однородной макронапряженности электрического поля. Коэффициенты С(г), Х(г) и е(г) дифференциального оператора (I) - квазипериодические случайные быстро осциллирующие функции координат г,

С(г) = co(r)CF + (1 - c^r)^^, e(r) = ®(r)eF + (1 - <о(г))ем ,(2) l(r)-co(r)XF+(l-®(r))kM, где щ(г) - индикаторная функция включений (равна 1 во включениях и 0 в матрице), С, е, X - тензоры упругих, пьезомеханических и диэлектрических свойств включений ( F) и матрицы ( М) композита соответственно.

Метод периодических составляющих

Метод периодических составляющих [1] основан на выделении из полей коэффициентов С(г), Х(г), е(г) и из искомых полей перемещений и (г) и потенциала (р(г) соответственно периодических коэффициентов СУ (г), Хр(г), ер(г) и решений <У (г), <рр (г) краевой задачи для композита с периодической структурой fc (г)<„ (г)] . + Vnij (г)Ф^ (г)] у = 0, к ом (г)] у - к» о^,* ок - ° >

Решение краевой задачи (3) будем считать известным

«/4r) = E*ry +^,,(1)^+6^(r^ <рДг) = -£Уу + /XO)eL+^0)^’.       (4)

где a^p(r), 1У(г), f^(г) и h^p(r) - периодические функции координат; решение (4) может быть определено методами, изложенными в работах [8-10]. Через СУ*, V* и е^р* обозначим тензоры эффективных упругих свойств, диэлектрической проницаемости и пьезомеханических свойств композита с периодической структурой соответственно.

Разложения коэффициентов

С(г) = СР (г) + С (г), л(г) = V (г) + Г (г), е(г) = ер (г) 4- е° (г)

и искомых решений

'                     u(r)=:UP(r)+U°(t),

ф(г) = ф ^ (г) + ф° (г)

позволили перейти от краевой задачи (1) с неоднородными граничными условиями для полей перемещений u(r) и электрического потенциала ф(г) к решению краевой задачи h™ Wm>n (г)] у + ky (г)ф;„ (r)^ + х, (г) = о, [Мг)фДг)]у. - tN(r)«^(r)] . + У(г) = о

с однородными граничными условиями

и°|Г=0, ф°г = 0 для искомых полей

отклонений н° (г) и ф° (г), где поля

ХМ = [c^^X,»^ + к_у(г)фДг)]., У(г) = ^(rXfr)^ - к^ДНи^Дг)]^.

Для решения задачи (5) может быть применен метод функций Грина G(r,r₁ ) и 5(г,г_} ), например, для однородной среды с осредненными по объему композита электроупругими свойствами [7]. Эти функции являются решениями уравнений

Стк,^гХ\ ) = -5й5(г-г( ), <Ху >^(г,Г| ) = -8(г-г, )       (6)

и вместе со своими производными обращаются на бесконечности в ноль, 5(г - г, ) - обобщенная дельта-функция, б - символы Кронекера. Далее, осуществим переход от дифференциальной постановки краевой задачи (5) к решению системы интегро-дифференциальных уравнений, например, методом последовательных приближений [1, 7]. В результате искомое решение примет вид

u°(r) = ^U°w(r),*=|

^^«^

к=\

где первое приближение (£=1)

^ (г) = Jc_y (г, г, )[с;„„ (г, ^Р, (г,) + е^(г, X (г, )]_$ аг, V

/'^'Цг) = Jecr,^ )[xyr^

V*

последующие (к = 2, 3, ,..) члены рядов (7) вычисляются по рекуррентным последовательностям•

Uf\r)-ГДг.г, )[с^Дг,М^^,

V'

^(г)= ^(г.г, ^Л^^’Чг^^^.

V

Сингулярное приближение

Сингулярное приближение основано на использовании в решении (7) предполагаемого равенства вторых производных функций Грина G^^^r,^ ), Q^t^r ) своим сингулярным составляющим [3, 4, 7]

VVG(r,r, )-G"8(r-r1 ),

WQ^rJ^Q^r-rJ.

Вторые производные функций Грина VVG(r?ri ) и VVQ(r,r, ) представляют собой обобщенные функции и поэтому они определяются интегрально: компоненты Gs и Q5 в (8) рассчитываются по формулам [7]

G5 = JVVG(xXx = fVG(x)ds„ , Qs = JVVQ(x>/x = (VQ(xMs„ (9) Vo                    su                                         v«                    s« через первые производные функций Грина, где s0 - поверхностость области v0 -“зерна неоднородности” [7], включающего особую точку х-0, где х = г, —г. В этой точке функции VVG и VVQ имеют особенности. Геометрией зерна неоднородности можно учесть не только геометрическую форму включений, но и анизотропию их разупорядочивания в объеме композита.

Решение для тензоров эффективных электроупругих свойств квази периодического композита в сингулярном приближении метода периодических составляющих имеет вид

Су™ = РсСп + (1 - ^с^,  х* = р\с + (1 - р^к:, rhkv е.тп " P«Cn + 0 - Р^^Ы, > bh где С* - тензор эффективных упругих свойств, X* - тензор диэлектрической проводимости и е* - тензор пьезомеханических свойств квазипери одического композита, разупорядоченность включений в квазипериоди ческой структуре в расчетных формулах (10) учитывается через тензоры анизотропии разупорядоченности а(1), а(2), а(3> и коэффициент периодичности р [3, 4], Тензоры анизотропии разупорядоченности включений в квазипериодической структуре введены в решении (10) равенствами

Г¹⁵* — Л(0 r^si*                  15/*      ,5*     -43) si*                            /1

^ijmn ^— ^ijmn ^rhkv >    ^ij ^ijrh ^"rh ’    ^imn ^— ®imn ^krh ’                         (11)

rhkv                                               krh где тензоры эффективных электроупругих свойств С5*, е5* и Xs* среды «статистическая смесь» рассчитываем по формулам

С⁵‘ =+v₀(l-vj[c--A^s — ё-F^J, I^s* = +v, O -vjlx H' + ё-В^$], е^$* ^o+vjl-vjjcH'-C-B^

с учетом решений

А^П^Ць^-а^-а^-Ь^),

Р^М.^-а^-а^-Ь®)

0 5 - 000 . L0)-_a(U)  (2,2)-1  (2))

H>=ti<2H.(C(2)_a(2J).^^

где

Q<0       -я^2) .я(2’2Н .a(2J)

а^Л - I G' -СУ-ML a(2J) Q [+5(l-2vj], b(1) = GS -C.b^ = -QJ ё,

П(д^ав.2)_я(ед..а(ин...а<и)8 a°'2) =G5 ■ ■[+e(l-2vo)], ,a^2>=-6 + Q^ T(l-2v„), ^»-G*-e#    c^^-Q^-X

(здесь G⁵ - симметричная составляющая G^_mn по первой паре индексов). В структуре «статистическая смесь» отсутствует корреляция физико-механических свойств в различных точках среды [1].

Для квазипериодического композита с изотропной разупорядоченностью включений тензоры анизотропии разупорядоченности (11) примут вид а⁰¹ =11, а⁽²⁾ = 1, а⁽³⁾ = d I, и формулы (10) преобразуются к виду

С* = рС^р*^(\-р^\ X* = рХ^р* + (1-^)Х^, е* = рй^р*^<\-рУ’* (12)

или С = С^Р Ч-А^\ X = к^р* + А⁽²⁾, е*=е^;з*+А⁽³\ где & = !-/> - коэффициент хаотичности, A^(l) = h^2^st*-С^р*^ ^ = h^k^sl*-Х^Р*У А⁽³⁾ = h (е⁵'* -е^р* ) -поправки к тензорам эффективных упругих С^р* , диэлектрических к^р* и пьезомеханических е^р* свойств композита с периодической структурой, обусловленные разупорядоченностью включений.

Численный расчет. Сферические поры в пьезоакерамике

Пусть квазипериодическая структура пьезокомпозита (рисунок, табл. 1) образована независимыми для каждой ячейки случайными отклонениями а центров сферических включений (пор) детерминированного радиуса r_F от узлов правильной решетки с ячейкой периодичности в виде куба. Свойство квазипериодичности структуры и независимость случайных отклонений а для различных ячеек позволяет перейти к рассмотрению одиночной ячейки квазипериодичности на рисунке, б. Все ориентации случайного вектора смещений а равновероятны, и его величина |а| распределена по равномерному закону на отрезке [0; А], где А = ^А_тах, ке [0; 1] -степень разупорядоченности сферических включений, величина максимально допустимого смещения А_тах = ^(7/(2^)-!), где Т - период или ребро кубической ячейки.

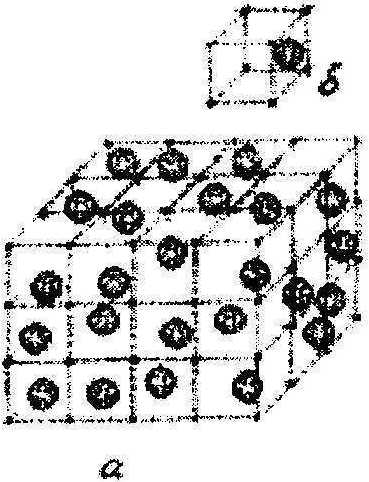
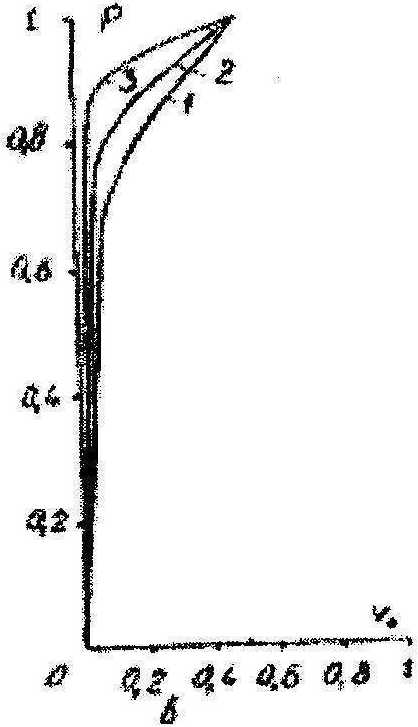
Рис. Ячейка квазипериодичности (б) и коэффициент периодичности р (в) для степени разупорядоченности к^\ (1), 2/3 (2) и 1/3 (3) сферических пор в пьезо керамике (а)

Таблица 1

Упругие постоянные, 1010 Па					Относительные диэлектрические постоянные		Пьезоэлектрические постоянные, Кл/м2
сн	с12		сзз	с44	X) /Хо	Х3/Хо	е31	езз	^15
13,9	7,78	7,43	11,5	2,56	730	635	-5,2	15,1	12,7

Электроупругие свойства пьезокерамики PZT-4 [5, 6] (без пор)

В табл. 2 представлены результаты влияния величины относительного объемного содержания сферических пор v₀ на отклонения А^е = (с* ~с^м^с^м 100%, А^е = (е*-е^У^ ■ 100%, А^?'=(х* -X^/X^ -100% значений компонент матриц эффективных упругих, пьезоэлектрических и диэлектрических трансверсальноизотропных свойств пьезоакерамики PZT-4 с квазипериодическим распределением пор (рисунок, а) для значения степени разупорядоченности пор к^Х от соответствующих постоянных пьезокерамики без пор (см. табл. 1); диэлектрическая постоянная вакуума л₀ = 1/(36л)1(Г⁹ Ф/м = 8,85 10”¹² Ф/м.

Таблица 2

Влияние содержания сферических пор на относительные изменения эффективных постоянных пьезокерамики PZT-4

Параметры структуры		Ас,%
V	Р	С11 ” с22	4		сзз		С)3		С44 - с55		<4
0,2	0,1	-46%		55%	-44%		-56%		-27%		-35%
0,5	0,39	-79%		86%	-78%		-87%		-65%		-71%
						А"	, Ах,%
				^33		е15	" е24	Хи -Х22		^33
0,2	0,1	-35%		-42%		-42%			-19%		-18%
0,5	0,39	-75%		-80%		-80%			-56%		-54%

Заключение

Методом периодических составляющих [1-4] получено решение связанной краевой задачи электроупругости для пьезоактивных композитов [5, 6] со случайными квазипериодическими структурами для полей отклонений искомых решений:

потенциала, напряженности электрического поля и полей деформирования от соответствующих решений для композита с идеальной периодической структурой. Аналитические решения для тензоров эффективных упругих, пьезомеханических и диэлектрических свойств квазипериодических композитов в сингулярном приближении представлены через известные решения для идеальной периодической структуры, среды типа «статистическая смесь», и структурные параметры квазипериодической структуры: тензоры анизотропии разупорядочивания и коэффициенты периодичности и хаотичности. Приведены результаты численного расчета эффективных электроупругих модулей трансверсально изотропной пьезокерамики PZT-4 со сферическими порами.

Работа выполнена по гранту РФФИ-Урал № 02-01-96403.