Элементы баллистического расчета при гравитационном маневре космического аппарата

Если перемещение тела при падении пренебрежимо мало по сравнению с расстоянием до центра тяготения, то ускорение свободного падения является практически неизменным. При этом задача установления параметров падения не представляет трудности. Далее этот случай не рассматривается.

1. Задача о скорости и времени падения тела

Падающее в вакууме тело имеет ускорение a =

d ² r dtf

M

^- G — , r

где G – гравитационная постоянная, M – масса планеты, r – мгновенное расстояние между телом и центром планеты. Исходное расстояние равно R. Знак «-» обусловлен противоположными направлениями векторов a и r. Масса тела пренебрежимо мала по сравнению с М.

Дифференциальное уравнение (1) решается следующим образом.

dr     . . d ² r dv

— = v (r), —- = —, dt           dt2

dv dv dr dv dr dv

— =--=--= — v, dt   dt dr dr dtdr d2 r dv   dv

—V = —v, —v = - G —7, dt2   dr    drr dr vdv = - GM —, r

vr

J vdv = - GM j —, 0               Rr

v- = GM ¹

2 r

(оСМИЧЕскиЕ

АППАРАТЫ И

Том 5

Знак и выше.

V „

— = GM

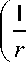
R

v = -V 2 GM ¹ --.

rR

Доказательство 1 .

a + x .2                .2, .2

-----= t , a + x = t b - 1 x, b - x

«–» обусловлен той же причиной, что

2x                   12 b — a x (1 +t ) = t b - a, x =----—

1 + 1²

dr dt

- V 2 GM ¹ - -, rR

dx =

2 tbdt   t ² b - a

-------:---~ 1 + 1 ² ( 1 + 1 ² ) ²

2 tdt ,

r dr =

R - r

2 GM dt

R

a + x

b — x

t

2 tb

t^b — a

2. Табличный интеграл

( 1 + • ² ) ²

2 t

dt =

t^b — a

Для решения дифференциального уравнения (4) формально подходит табличный интеграл [1–3]:

( 1 + t ² ) ²

2 1 ² dt =

I

J a + x

----dx = - J( a + x )( b - x ) b - x

=2 b J

1 + 11

^“

1 + 11

dt

^“

- ( a + b ) arcsin

b - x + C .

a + b

■2 b J

t ⁴

^~

1 ² a/b + 2 11

^“

( 1 + 1 ² ) ²

2 1 ² + 1 - 1 , --------d1 =

Оказалось, однако, что эта формула недостоверна, а именно, производная правой части не равна подынтегральному выражению. Действительно,

= 2b J dt - 2 b J

1 + 1 t

dt

-

- 2 b J dt + 2 b J

t aj b + 2 1 + 1

=---,            (-а + b - 2 x) + dx 2 J(а + x)(b - x)

( 1 + 1 ² ) ²

-dt =

+ ( a + b )

1        1

a + b

- 2 b J

1 + 1 ²

dt +

I b - x 2 V b - x

1-- a + b

+

t ² + 1 ( a/b + 2 ) + 1 - 1

( 1 + 1 ² ) ²

-dt =

a - b + 2 x     ( a + b ) V a + b a + b

2^( a + x )( b - x )    2 V a + x ^b - x

= - 2 b arctg t + 2 b ( a^b + 2 ) J

dt

1 + 1^г

-

a - b + 2 x + ( a + b ) ² 2^( a + x )( b - x )

- 2 b ( a^b + 2 )

a + b

dt

a

+ 2 b ^J( 1 + 1 ² ) 2

Таким образом, этот табличный интеграл применять нельзя.

3. Корректировка табличного интеграла

= - 2 b arctg t + 2 b ( a[b + 2 ) arctg t

- 2 b

a + 2 b a + b 1

b

Теорема : Справедлива следующая формула:

a + x               a + x

----dx = ( a + - )arctg

- — x              - — — x

t

a + 2 b 2 ( 1 + 1 ²

-

+ arctg t I + C =

= - 2 b arctg t + 2 b ( a/b + 2 ) arctg t -

( a + b ) t 1 + 1 t

- ( a + b )arctg t + C =

— ^ ( - — x )( a + x ) + C .

= ( a + b ) I arctg t -

t

1 + 1 ²

+ C =

a + x

= ( a + b )arctg a + x - ( a + b ) V b - x

У b - x

1 +

a + x b - x

+ C =

R arctg

R - r

- R ^π- r ( R - r ) =

-

2 GM

_Rt ,

R

a + x       b - x a + x _

= ( a + b )arctg        - ( a + b )             + C =

V b - x        a + b y b - x

= ( a + b )arctg a + x - 4 ( b - x )( a + x ) + C . у b - x

Теорема доказана.

Доказательство 2 .

df- = ( a + b ) dx

, a + x

1 +-----

b - x

n

- —arctg

r

R — r

+ 4 r ( R - r ) =

2GM t. (7)

R

Это решение дифференциальных уравнений (4) и (1) является уравнением движения нормально падающего тела.

Из выражения (2) следует:

2 GMR r =------------- .•

2 GM + Rv v

Подстановка этого выражения в (7) дает:

R

П

- —arctg

2 GMR

2 GM + Rv v

—

1 b - x

2 у a + x

1 b - x

^{+ (} a ^{+ x} ) Tl ---\2 ^{( -} 1)

^{( b - x} )

---.       ^— ( b - a - 2 x ) =

2 ^( a + x )( b - x )

( a + b )( b - x )   b - x b - x + a + x

=       '       ' J--"---- 3--

2( a + b )     a + x  ( b - x )

b - a - 2 x

24(a + x )( b - x )

_ 1 b - x a + b     b - a - 2 x

2 У a + x b - x  2^( a + x )( b - x )

a + b         b - a - 2 x

2y/( a + x )( b - x )  2^( a + x )( b - x )

2 a + 2 x

2^/( a + x )( b - x )

a + x b - x

Теорема доказана.

4. Продолжение решения исходной задачи

-

+

R

Интегрирование дифференциального уравнения (4) в соответствии с (6) дает:

r ∫ R

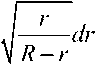
12GM R

t j dt, 0

r

R arctg

R - r

- 4 r ( R - r )

R

2 GM R

t j dt, 0

2 GMR

2 GM + Rv ²

2 GMR

2 GM + Rv²

2 GMR

R --7

2 GM + Rv v

2 GM

R  ^{t ,}

n

n

2 GMR

2 GMR + R ² v ² - 2 GMR _v

+

2 GMR ( 2 GMR + R ² v ² - 2 GMR )    R GM

( 2 GM + Rv ² ) 2           * ^R

- arctg

2 GMR Rv

v 2 GMR

2GM + Rv v

2 GM t

RR

Это временная функция скорости.

Для получения временной функции ускорения следует (1) подставить в (7).

^^^^H

arc tg

( GMa ¹ ) ¹²

R - ( GMa ¹ ) ¹²

+^ ( GMa ¹ ) ¹² ( R - ( GMa ) ¹² ) = 2 GMz .

В соответствии с (7) период падения тела на поверхность планеты равен:

R

П

- - arctg

R — R m J

+

+V R m ( R - R m ) =

2 GM _T

R ’

где R_M – радиус планеты.

КИЕ АППАРАТЫ И

В соответствии с (3) скорость тела у поверхности планеты равна:

Том 5

Таблица

V = - v 2 GM

11

—

^R M ^R

Сравнение результатов расчета периода падения тела

Пример.

R = 7∙10⁶ м, параметры планеты

не отличают-

ся от земных. R_M = 6,371∙10⁶ м; М = 5,9726∙10²⁴ кг;

G = 6,6743^10^-11 м³/(кг^с²).

В соответствии с (8):

_ , „ = п

7 - 10   -- arctg

----~-----а ---А

6,371-106

\ (7 -6,371)-106

+

Параметр	Значение
Период падения тела на основе некорректного интеграла (5)	405,169 с
Период падения тела на основе предложенной методики	387,275 с
Абсолютная погрешность	+17,894 с
Относительная погрешность	4,62%

+76,371-106(7 - 6,371)-106 =

Заключение

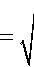
2⋅6,6743⋅10-11 ⋅5,9726⋅10247 ⋅106

Период падения тела на поверхность планеты равен: Т = 387,275 с = 6,455 мин.

В соответствии с (9) скорость тела у поверхности планеты равна:

V =-2⋅6,6743⋅10-11⋅5,9726⋅1024 ⋅

⋅

6,371 ⋅ 10 ⁶

= 3353,297 м/с.

7 ⋅ 10 ⁶

В таблице представлено сравнение значений периода падения тела на поверхность планеты из примера и полученного на основе использования некорректного табличного интеграла (5).

Трудно представить, что никто и никогда не искал формулы времени, скорости и ускорения при нормальном свободном падении тела. Однако если при этом использовался табличный интеграл (5), то, конечно, те формулы неверны. Поводом усомниться в интеграле (5) послужило то, что в ряде конкретных случаев значения аргумента у арксинуса превышали единицу.

Корректировка этого интеграла (6) особенно актуальна с учетом его очевидного прикладного характера.

Полученные результаты могут быть полезны при расчетах пассивного гравитационного маневра при межпланетных полетах [4–6] и расчетах отвесного падения небольших небесных тел и отработанных элементов конструкций космических аппаратов [7–10].