Элементы численного вероятностного анализа

В последнее время возрос интерес и увеличилась исследовательская активность в области теории и практики анализа данных больших объемов. Такие объемы информации, с одной стороны, позволяют получить более точное описание объекта исследования, а с другой - превращают поиск решений в сложную задачу, требующую применения современных математических методов обработки и анализа информации, в том числе разработки численных методов, позволяющих определять функции от случайных аргументов и осуществлять операции над ними.

В настоящее время в практике принятия управленческих решений, например при оценке инвестиционных проектов в условиях высокой неопределенности и риска с успехом, используют метод Монте-Карло [1; 2]. Однако при всех положительных качествах этот метод обладает рядом недостатков, самыми существенными из которых являются низкая скорость сходимости и высокие вычислительные затраты, что вносит дополнительные сложности в работу с данными большого объема.

В рамках обозначенного направления анализа данных рассмотрим понятие численного вероятностного анализа как раздела вычислительной математики, предметом которого является решение задач со стохастическими неопределенностями в данных с использованием численных операций над плотностями вероятностей случайных величин и их функций. Одним из основных элементов численного вероятностного анализа является гистограммная арифметика, применение которой позволяет снизить уровень неопределенности в данных и получить дополнительную информацию о распределении случайных величин [3]. Идея гистограммного подхода изложена в работах [4; 5] и заключается в следующем: наряду с общим представлением плотностей вероятностей случайных величин в виде непрерывных функций можно рассматривать случайные величины, плотность распределения которых представляет гистограмму. Например, для одномерной случайной величины гистограмма P -кусочно-постоянная функция, которая определяет ся сеткой {xi | i = 0,...,n} и на каждом отрезке [ xi, xi+1] принимает постоянное значение Pi, h = max n=o1{xi+i - xi}.

Важным понятием численного вероятностного анализа является понятие вероятностного расширения. Определим это понятие в рамках гистограммного подхода. Для этого рассмотрим задачу определения закона распределения функции нескольких случайных аргументов.

Пусть имеется система непрерывных случайных величин (x1,..., xn) с плотностью распределения p(x1,..., xn). Случайная величина z связана с системой (x1,...,xn) функциональной зависимостью z = f(x1,..., xn ).

Тогда плотность вероятности случайной величины z будем называть вероятностным расширением функции f.

На основе понятия вероятностного расширения определим гистограммно е вероятностно е расширение. Пусть гистограмма F определяется сеткой { z i | i = 0 ,..., n }. Зададим область О i = {( x^..., x_n ) | z i <  f ( x ₁ ,..., x_n ) <  z i _{+ 1}}. Тогда значение гистограммы F i на отрезке [ z i , z i _{+ 1}] имеет вид [3]:

F = J p &,..., ^ n ) d 5р .. d 5 n I ( z _M - z i ). (1) Q i

Гистограмму F , построенную по (1), будем называть вероятностным гистограммным расширениемf.

Далее построим гистограммные вероятностные расширения для арифметических операций над случайными величинами. Пусть P - гистограмма плотности вероятности z = x * y , где * е { +, -, ■, I, Т }. Тогда на интервале [ z i , z i _{+ 1}]

P i = J Р ( x 1 , x 2 ) dx dx 2 1 ( z i + 1 - z i ) ,

Qi где Qi = {(x1, x2) 1 zi < x1 * x2 < zi+1} [4].

Операция max( x , y ) определяется через функцию распределения F : zz

F ( z ) = J P_x ©d ^ J P_y ©d £

-ю        -ю

Пусть f ( x₁ ,..., x n ) - рациональная функция. Тогда для вычисления гистограммы F заменим арифметические операции гистограммными, а переменные x 1 , x 2 , ..., x n – их гистограммными значениями. Полученную гистограмму F будем называть естественным гистограммным расширением .

Теорема 1. Пусть f ( x 1 , ..., x n ) - рациональная функция, каждая переменная которой встречается только один раз и x 1 , ..., x n - независимые случайные величины. Тогда естественное гистограммное расширение аппроксимирует вероятностное расширение с точностью O ( h ^α).

Доказательство проведем по индукции. Для n = 2 утверждение справедливо [4]. Пусть это утверждение справедливо и для n = k и гистограмма F k аппроксимирует плотность вероятности функции f ( x₁ ,..., x_k ) с некоторой точностью O ( h ^α). Покажем, что это справедливо и для n = к + 1. Действительно, F k + 1 = F k * ^xk + 1 , ^но

F k + 1 - ^{f ( x} 1 ,-, x k , x k + 1 ) =

= (F k - ^f (^x 1 , •••, x k )) * x k + 1 ⁵ Ch “ * ^suPP { x k + 1 }.

Теорема доказана.

Рассмотрим пример, который иллюстрирует теорему 1. Пусть функция представлена в виде f (x, y) = xy + x + y +1 = (x +1)(y + 1) .

Заметим, что только второе представление функции в виде произведения двух сомножителей подпадает под условие теоремы 1 и, следовательно, естественное гистограммное расширение будет аппроксимировать вероятностное с точностью O ( h ^α).

Теорема 2. Пусть для функции f ( x ₁,..., x n ) возможна замена переменных, такая что f ( z ₁, ..., z_k ) -рациональная функция от переменных z ₁, ..., z_k , удовлетворяющая условиям теоремы 1, и z i – функции от множества переменных x i , i е Ind i , причем множества Ind i попарно не пересекаются. Пусть для каждой функции z i можно построить вероятностное расширение. Тогда естественное расширение f ( z ₁, ..., z_k ) будет аппроксимировать вероятностное расширение ^{f (}Д,-, x n ).

Пример 1. Пусть f (x1, x2) = (-x2 + x1)sin(x2). Тогда z1 = (-x2 + x1) и z2 = sin(x2). Заметим, что можно построить вероятностные расширения функций z1 , z2, где f = z1 z2 - рациональная функция, подпа- дающая под условия теоремы 1. Следовательно, естественное расширение этой функции будет аппроксимировать вероятностное расширение f (x1, x2).

Рассмотрим случай, когда для f ( x ₁ ,..., x n ) необходимо найти вероятностное расширение f , но не удается построить замену переменных согласно теореме 2. Пусть для определенности только x 1 встречается несколько раз. Заметим, что если подставить вместо случайной величины x 1 детерминированную t , то для функции f ( t , x 2 , ..., x n ) можно построить естественное вероятностное расширение. Пусть t – дискретная случайная величина, аппроксимирующая x 1 следующим образом: t принимает значения t i с вероятностью P i - и пусть для каждой f ( t i , x 2 , ..., x n ) можно построить естественное вероятностное расширение φ i . Тогда вероятностное расширение f функции f ( x ^..., x n ) можно аппроксимировать плотностью вероятности φ следующим образом:

n Ф(^> = £ P i фД) .

i = 1

Пример 2. Пусть f ( x , y ) = x ² y + x , где x , y - равномерные случайные величины, заданные на [0 , 1]. Заменим x дискретной случайной величиной t , { t i | t i = ( i - 0 . 5) / n , i = 1 , 2 ,..., n }, P i = 1 / n . Далее вычислим естественные вероятностные расширения φ i (табл. 1). Сравнение φ и f , вероятностного расширения f ( x , y ) показывает хорошее приближение: ф аппроксимирует f с порядком a = 1,499 8.

Таблица 1

Погрешность аппроксимации вероятностных расширений

n	II f - ф |1 2
10	1,2887825282 E – 03
20	4,5592973952 E – 04
40	1,6120775967 E – 04
80	5,6996092139 E – 05
160	2,0151185588 E – 05

Важно отметить, что число арифметических операций для вычисления x * y имеет порядок O ( n ²), где n – размерность сетки гистограмм. Гистограмма как кусочно-постоянная функция приближает плотность вероятности с точностью O (1 / n ). Однако уже средние точки гистограмм приближают плотность вероятности с точностью O (1 / n ²). Как показано в [4], нижняя оценка скорости сходимости гистограммных расширений к вероятностным имеет значение a = 1 (реально это значение несколько выше). Численные же эксперименты подтвердили, что в условиях теоремы 1 при правильном согласовании сеток гистограмм и использовании более тонких способов интегрирования гистограммные расширения имеют скорость сходимости a ® 2 .

Сравним полученные результаты с методом Монте-Карло. Известно, что метод Монте-Карло имеет сходимость O (1 / V N ), где N - число повторов [1]. Гистограммные же расширения имеют скорость сходимости O (1 / n ^а).

Пусть необходимо достигнуть точности ε. Число операций метода Монте-Карло при этом составит O (е ^{- 2}), число операций с гистограммной арифметики - O (е 2 ^а), следовательно гистограммная арифметика при а >  1 эффективнее метода Монте-Карло примерно в O (е ^{- 2(1 - 1 / а)}) раз.

Проиллюстрируем эффективность гистограммной арифметики на численном примере.

Пример 3. Пусть требуется найти сумму трех равномерно распределенных на [0, 1] случайных величин. Вычисления при n = 30 показывают, что ошибка при использовании численных операций гистограммной арифметики в норме l 2 составляет 1,1680Е – 03; ошибка метода Монте-Карло при числе бросаний N = 10 5 равна 5,4601E - 03, а при числе бросаний N = 10⁶ - 2,0284Е - 03, что сравнимо с погрешностью гистограммной арифметики. При этом число арифметических операций гистограммной арифметики определяется величиной порядка 30 2 или 10 3 , а метода Монте-Карло – величиной порядка 10 6 . Таким образом, в данном примере гистограммная арифметика эффективнее метода Монте-Карло примерно в тысячу раз.

Для решения ряда практических задач необходимо решать системы линейных и нелинейных уравнений. Методы их решений рассмотрены в работе [3].

В случае нахождения корня одномерного уравнения f ( x , k ) = 0, где k - случайный вектор параметров, предположим, что корень локализован на отрезке [ a , b ], ф z - вероятностное расширение f ( z , k ), z e [ a , b ]. Тогда P ( z ) есть вероятность, что корень лежит левее (правее) точки z :

P ( z ) = J ф z G) d £ (2) -X

Применение численного вероятностного анализа рассмотрим на примере.

Пример 4. Пусть завод производит некоторую продукцию и осуществляет ее реализацию. По наблюдениям известна гистограмма Y i покупок i- го товара, например, за неделю. Это означает, что известна плотность вероятности продажи товара P i , Y ^{e [} у , M

Пусть доход Di линейно зависит от продажи товара D = a Yi. Будем считать, что производство i-го товара не зависит от производства других товаров. Тогда общий доход будет просто суммой всех доходов по продажам всех товаров. Поэтому мы можем рассмотреть производство только одного вида продукции и для простоты индекс опустим.

Применим гипотезу: завод несет убытки, если товар произведен в объеме R , но продано Y <  R . Величина убытков U линейно зависит от разницы в( Y - R ) <  0 .

Пусть завод произвел товар объемом R . Оценим возможный доход:

R

D = ^a J p ⁽ у ) ydy ,

y

и возможный убыток

R

U = P J P ⁽ у ⁾⁽ у ^{- R} ) dy .

y

Заметим, что в этой постановке нам нужно максимизировать сумму D + U ^ max:

RR

f ^{( R} ) = ⁽ D + U ^{)( R} ) = ^a J p ⁽ у ) у dy + ^e J p ⁽ у ⁾⁽ у - ^R ) dy = yy

RR

= ^{(a + в)} J P ⁽ у ) у ^dУ ^- Р ^R J P ⁽ у ) ^dУ ^ max. yy

Приведем графики зависимости «производство– прибыль» при различных значениях параметров α и β (рис. 1). В расчетах величина α = 1, кривые 1 – 5 соответствуют значениям β = 0,3 (кривая 1 ), β = 0,4 (кривая 2 ), β = 0,5 (кривая 3 ), β = 0,7 (кривая 4 ), β = 1 (кривая 5 ).

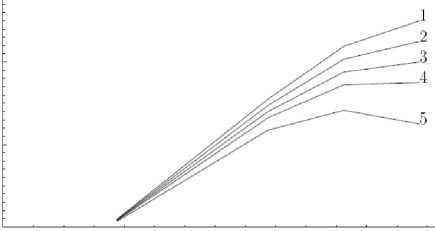
Рис. 1. Графики зависимости «производство–прибыль»

Таким образом, при небольших значениях β увеличение производства покрывает возможные убытки перепроизводства, но при сравнительно больших значениях β величину производства R следует ограничивать исходя из максимального значения D + U .

В качестве примера использования численных операций над гистограммными переменными рассмотрим задачу принятия решения об инвестировании проекта выпуска лекарственного препарата [2].

Пример 5. Компания рассматривает вопрос о приобретении для последующего производства патента нового лекарственного препарата. Стоимость патента составляет 3,4 млн долл. Решение принимается на основе анализа дисконтированных денежных потоков по значениям рассчитанных показателей NPV и IRR. Горизонт расчетов – три года. Согласно прогнозам, компания в первый, второй и третий годы реализации проекта продаст соответственно 802 тыс., 967 тыс. и 1 132 тыс. упаковок лекарства по цене 6, 6,05 и 6,10 долл. за упаковку. Ставка налога на прибыль равна 32 %, ставка дисконтирования – 10 %, себестоимость – 55 %, операционные издержки – 15 % от цены препарата.

По результатам расчетов IRR проекта составляет 15 %, а NPV – 344,8 тыс. долл. Стандартная финансовая модель приведена в табл. 2.

В данном случае мы имеем дело с высоким уровнем рыночной неопределенности, поэтому стандартная финансовая модель не дает достаточных оснований для принятия решения. Для одновременного учета неопределенности в цене, продажах, себестоимости и издержках применяется численный вероятностный анализ. Основные параметры финансовой модели: цена и объем продаж – моделируются как случайные переменные, имеющие вероятностное распределение. Численный вероятностный анализ позволит понять, какие факторы повлияют на финансовые результаты проекта в наибольшей степени.

Для моделирования цены продажи (отдельно за первый, второй и третий год реализации проекта) используется треугольное распределение.

Данное распределение имеет три параметра: минимальное значение, максимальное значение и наиболее вероятное значение. Цена продажи в первый год имеет минимальное значение 5,90 долл., максимальное значение – 6,10 долл., наиболее вероятное значение – 6,00 долл. Аналогично цена продажи во второй год имеет треугольное распределение с параметрами 5,95, 6,05, 6,15 долл. Цена продажи на третий год имеет треугольное распределение с параметрами 6,00, 6,10, 6,20 долл.

Объем продаж моделируется как случайная переменная с нормальным распределением. При этом в первый год нормальное распределение имеет среднее значение (математическое ожидание) 802 тыс. долл. и стандартное отклонение 25 тыс. долл., во второй год – 967 тыс. долл. и 30 тыс. долл. и в третий год – 1 132 тыс. долл. и 25 тыс. долл. соответственно. Предполагается, что себестоимость (процент от продаж)

имеет треугольное распределение с минимальным значением 50 %, максимальным значением 65 % и наиболее вероятным значением 55 %.

Следует отметить, что в данном случае треугольное распределение имеет не симметричную форму, а немного скошено вправо. Поэтому велика вероятность того, что себестоимость будет завышена, а не занижена по сравнению с наиболее вероятным значением. Операционные издержки (процент от продаж) моделируются с нормальным распределением с ожиданием 15 % и стандартным отклонением 2 %.

Для данного проекта NPV вычислялся по формуле

NPV( r ) = 0,8181818 • 0,68 z 1 S j x

3 x ^

i = 1

c _i x _i

(1 + r ) i

- 3 400 000,

где c i – цена в i -й год; x i – продажи в i -й год; s 1 – себестоимость; z 1 – издержки. Заметим, что в этой формуле каждая случайная величина встречается только один раз.

Расчеты велись при размерности гистограмм n = 50. Сравнение вычисления NPV методом Монте-Карло показало, что при числе экспериментов N = 1000 000 результаты совпадают с гистограммным расчетом с точностью до трех-четырех знаков после запятой. Численные эксперименты продемонстрировали, что при этом гистограммная арифметика более чем в триста раз быстрее.

Внутренняя норма доходности IRR определяет максимально приемлемую ставку дисконта, при которой можно инвестировать средства без каких-либо потерь для собственника: IRR = r , и при которой NPV( r ) = 0 .

Для вычисления IRR необходимо решать нелинейные уравнения. В случае гистограммного анализа использовалась формула (2). Таким образом, вычисление гистограммы корня нелинейного уравнения свелось к вычислению соответствующих интегралов от гистограммных расширений.

Анализ гистограмм NPV и IRR (рис. 2) показывает, что вероятны как крайне негативные исходы, так и значительная прибыль по сравнению со стандартным анализом.

Стандартная финансовая модель

Таблица 2

Показатель	Год 0	Год 1	Год 2	Год 3
Цена упаковки, долл.	–	6,00	6,05	6,10
Количество проданных штук	–	802 000	967 000	1 132 000
Выручка, долл.	–	4 812 000	5 850 350	6 905 200
Себестоимость, долл.	–	2 646 600	3 217 693	3 797 860
Валовая прибыль, долл.	–	2 165 400	2 632 658	3 107 340
Операционные издержки, долл.	–	324 810	394 899	466 101
Чистый доход до налогов, долл.	–	840 590	2 237 759	2 641 239
Налоги, долл.	–	588 989	716 083	845 196
Стартовые инвестиции, долл.	3 400 000	–	–	–
Чистый доход, долл.	3 400 000	251 601	1 521 676	1 796 043

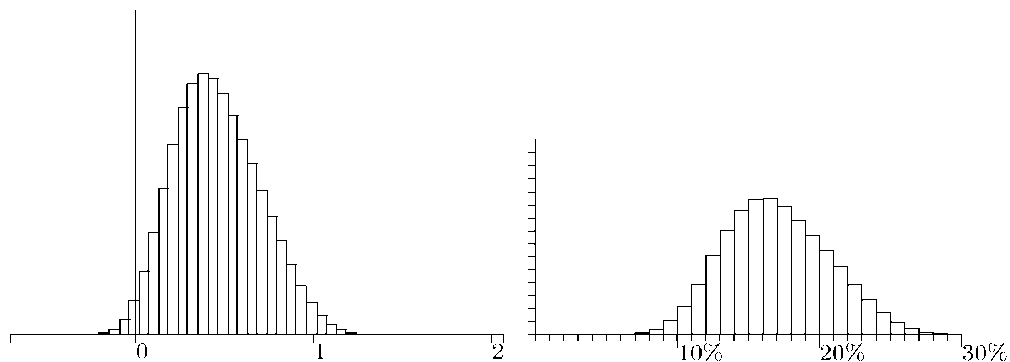
Рис. 2. Гистограммы NPV и IRR

На основании последнего примера можно сделать вывод о том, что применение гистограммной арифметики в рамках технологии визуально-интерактивного моделирования (ВИМ) [6] позволяет лицу, принимающему решение, увидеть возможные варианты негативных исходов реализации проекта в отличие от стандартного анализа, который дает только положительный ответ.

Таким образом, проведенные авторами теоретические и практические исследования приводяи к двум основным выводам:

– гистограммная арифметика может рассматриваться как элемент численного вероятностного анализа, который позволяет работать с неопределенными данными в рамках различных практических приложений;

– гистограммная арифметика может использоваться как инструмент технологии визуально-интерактивного моделирования, что значительно повышает качество анализа возможных вариантов решений и дает удобное средство для их принятия.