Элементы фрактальной теории видовой структуры гидробиоценозов

1 Нижегородский государственный университет им.Н.И. Лобачевского,г. . Новгород 2 Институт экологии Волжского бассейна РАН,г.

В статье в тезисной форме представлены основные положения фрактальной теории видовой структу-ры сообществ (в первую очередь, видового богатства и видового разнообразия).

Физические условия и химический состав водной среды обуславливают специфические комбинации лимитирующих абиотических факторов, воздействующих на становление, развитие и функционирование гидробиоце-нозов . Гидробиоценозы являются сильно не-равновесными системами, связанными с пе-реносом интенсивных потоков вещества и энергии, и обладают имманентной структур-ной универсальностью, которую в настоящее время можно интерпретировать с позиции теории фракталов [1, 2, 4, 5, 8, 10]. Потоки энергии и вещества, проходящие через откры-тые системы, обеспечивают возникновение в них эффектов самоорганизации - образо-вание макроскопических диссипативных структур . Эти структуры очень часто демон-стрируют в широком диапазоне параметров пространственно-временной скейлинг -свойство самоподобия, или масштабной ин-вариантности - один из фундаментальных видов симметрий физического мира, играю-щих формообразующую роль во Вселенной. Пространственно-временной скейлинг ха-рактеризуется сильными, спадающими по сте-пенному закону, , которые ти-пичны для критических явлений . Поэтому ка-чественно динамика подобных систем про-изводит впечатление самоорганизованного и самонастраивающегося критического режима. Явления такого рода были объединены не-давно общим наименованием систем с само-организованной критичностью (self-organized criticality [17]). Самоорганизованная критич- ность соединяет в себе два направления со-временной физической парадигмы - самоор-ганизацию и критические явления - и актуа-лизирует новый подход к анализу сложного поведения нелинейных распределенных си-стем . Этот новый подход связывает динами-ку критических флуктуаций с появлением фракталов в конфигурационном пространстве нелинейной распределенной системы при кинетическом фазовом переходе.

Все это в полной мере относится к био-экологическим системам. Процесспроникно-вения теории фракталов в экологию можно условно разделить на три этапа. Первый из них был связан с необходимостью описания пространственной сложности тех или иных биотопов, в частности горных массивов, реч-ных систем, почвы, коралловых рифов и т. . На втором этапе пришел черед описания фрактального распределения отдельных ви-ДОВ. Наконец, на третьем этапе встал вопрос о самоподобии внутренней структуры самих сообществ.

В настоящей работе в тезисном виде пред-ставлены основные положения фрактальной теории видовой структуры сообществ (на примере гидробиоценозов) разрабатываемой в настоящее время авторами . В первом при-ближении ограничим рассмотрение видовой структуры анализом видового богатства (чис-ла видов), и относительными численностя-ми составляющих сообщество видов,т. . ви-довым разнообразием .

Видовое богатство

При анализе видового богатства ключевое значение имеет как его зависимость от пло-щади (species-area relationship, SAR), так и ха-рактер поведения кривой накопления видов в зависимости от объема выборки. История анализа SAR, имеющего, в основном, отно-шение к наземным местообитаниям и под-робно рассмотренная в нашей предыдущей работе [5], насчитывает уже около полутора столетий . Постановка вопроса о фрактальной структуре биотического сообщества является вполне логичной и в контексте дискуссии о видовом насыщении сообществ [3, 6 и др.]. Именно степенной закон, не предполагаю-щий насыщения функции f ( x ) , учитывает вклад редких видов, или видов с «единичной численностью» [20], не противоречит «пра-вилу экологической неаддитивности» Леви-ча [9] и, наконец, дает возможность приме-нить фрактальный формализм для характери-стики видовой структуры сообщества. Сле-дует отметить интересные перспективы, свя-занные с применением фрактального подхо-да к анализу таксономического разнообразия [13], а также «островных» сообществ, где в качестве «острова» могут выступать геогра-фические объекты, организмы или их части (лист - фитофаги - паразиты), системы орга-низмов, например, консорции, паразитарные системы, микробиоценозы семей обществен-пых насекомых и т. .

Специфика пространственного распреде-ления сообщества в водной среде заставляет обратиться к закономерности связи темпов накопления видов с увеличением объема выборки с позиции альфа-разнообразия Уит-текера [14]. Маргалеф [12], предложив сте-пенную зависимость числа видов ( S ) от сум-марной численности -

(N)S Nk, (1) тем самым, по-видимому, -нул фрактальную природу этой связи. Степей-ная зависимость в ортогональных координа-тах натуральных значений SиN легко преоб-разуется в линейную в билогарифмических координатах lnS k lnN , где k = lnS/lnN, 0 k 1 имеет смысл индек-са видового разнообразия Маргалефа. Выра-жение (1) показывает, сообщества (в данном случае в виде его ком-понента - видового богатства) инвариантна относительно преобразования его численно-сти . Величину k можно трактовать как соот-ветствующую фрактальную размерность: -ло элементов видовой структуры - число видов сообщества - меняется по степенному закону с показателем k при увеличении раз-меров системы,т. . с ростом численности сообщества. Таким образом, адекватным математическим образом накопления вида-вого богатства при росте выборочного уси-лия, являются монофракталы : , характеризующиеся единственной фрак-тальной размерностью.

Использование степенного закона для ана-лиза зависимости между видовым богат-ством выборки и ее размером начало полу-чать распространение относительно недав-но . Наличие фрактальной структуры для гид-робиоценозов разномасштабных водных объектов было показано в наших работах [8, 16]. Кроме того, наклоны степенной зави-симости (то есть фактически индекс Марга-лефа k ) часто обсуждаются в контексте влия-ния размера тела животных на структуру со-ответствующих сообществ [11, 18, 21].

На рис . 1 приведена экспериментальная зависимость числа видов макрозообентоса от его численности, полученная для ряда город-ских озер в Нижнем Новгороде . Видно, что точность определения показателя быстро увеличивается с ростом размера выборки. Необходимо подчеркнуть, что в отличие от регулярного математического фрактала для реального природного фрактала существует некоторый минимальный масштаб длины min , такой, что на расстояниях l » l_min его основ-

.

Кроме того, на достаточно больших масшта-бах длин l > l_max, где l max -

, самоподобия также нарушается . Поэтому свойства природных фракталов рассматрива-ются лишь на масштабах l, удовлетворяющих соотношению min max. В рассматри-

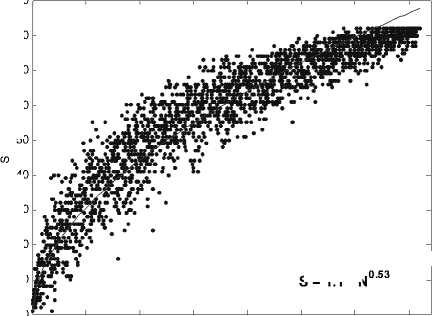
S = 1.1 * N

1000    1500    2000    2500    3000    3500

N

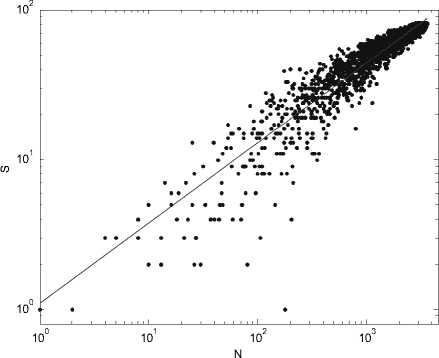
.1.                                                                                                                       .()                    ()

ваемом контексте фрактальности видового богатства сообщества эквивалентом масшта-ба длины является суммарная численность ( N ), что позволяет сформулировать следующее обобщение: фрактальная, структура -о-го объекта проявляется в асимптотике -

(N).                                         - рой критической N « Nшп его осиовное свойство - самоподобие - нарушается.

Видовое разнообразие

Мы видим, таким образом, что показатель Маргалефа (k) тоответствует фрактальной размерности (D) три описании регулярных фракталов . Однако сама по себе фрактальная размерность не дает исчерпывающего количе-ственного представления о структуре само -подобного объекта (мнтжества с одинаковой фрактальной размерностью могут иметь раз -личную структуру). В р тмках такого описания роли отдельных видов в формировании структуры сообщества нивелированы: зависимость фиксирует лишь факт наличия того или иного вида в выборке, итнорируя его представленность и степень доминирования. В реальности мы имеем дело с принципиаль-но неоднородным распределением особей выборки по видам реестра. Нтиболее общее описание внутреннего устройства самопо- добных объектов позволяет дать теория муль-тифракталов, характеризуемых бесконечной иерархией размерностей [15]. Основные понятия , лежащие в основе того, что теперь принято называть мультифракталами, были в в едены Мандельбротом [10] в начале 70-х годов прошлого века.

Нами разработаны и обоснованы алгорит-мы анализа и интерпретации мультифрак -тальных спектров как обобщенного геомет -рического образа видовой структуры гидро -биоценозов, отражающего его основные компоненты : видовое богатство и видовое разнообразие [5, 8]. В эксперименте исследователь имеет дело с относительными частота -ми распределения особей по видам. Пусть набор {pi } характеризует относительные частоты распределения особей по видам: р = N/N , чде N - число особей i -го вида, N - размер пробной выборки, a i пробегает значения от единицы до полного числа видов S(N) , обнаруженных в пробе. Вектор p = (p1 p_s) называется вектором относительной значи-мости видов. Сумма компонент этого вектора дает нам численность или размер выбор -ки, а количество ненулевых компонент дает число обнаруженных видов. Очевидно, что

Z м А^

Введем моменты распределения особей по видам и выясним характер их асимптотичес- кого поведения при увеличении численное-ти N:

n

Mq =z pi^q  N ^{т ( q )},                    (2)

i 1

где - ОО < q < оо - называется порядком момен-та, а показатель г( q ) характеризует скорость изменения соответствующего момента при увеличении размера выборки. Второе равен-ство в выражение (2) является обобщением формулы Маргалефа и, очевидно, совпадает с последней при q = 0 . Обобщенной размер-ностью D_q ( обобщенной размерностью Реньи ) распределения является убывающая функция q , вводимая определением [15]:

Dq

lim <

N

1 q

ln Mq ln N

£ ( q )

1 q ^,

На практике величины (3) можно оценить, используя несколько различающихся значений N , по более простой формуле

ln M D^{q q} 1 q ln N

.

Для q=0                 :

_{D k}   ln S ( N )

⁰ ln N

.

Можно показать, что для q = 1

i p_i ln p_i H

D ₁        i 1               , где H есть ни

1 lnN lnN что иное как информационный индекс видо-вого разнообразия Шеннона. Для q=2

lnC         1

D2 - 1 или N 2, где C - индекс lnNC доминирования,а1/C 1 /у iS 1 pi 2

видового разнообразия Симпсона. Для q = ln ц

1/2: D1/2       ‘ ИЛИ и = N D12, где м — извес- lnN тный в экологической литературе индекс

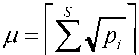
Заметим, i1

что для доли редких видов h 1- р) S [7], легко можно получить ^: h 1 N ^{D 1} ' 2 D 0 . Нео -

жиданным может показаться отсутствие клас-сических аналогов индексов разнообразия для размерностей Реньи с отрицательными q . Вместе с тем значение таких индексов пред-ставляется чрезвычайно важным при выяв-лении роли редких видов . Рассмотрим, на-пример, обобщенную размерность Реньи для

• 1    ln M ₁

q = -1 : D 1          , где наибольший вклад

• 2    ln N

в значение величины момента M-1, представ-ляющего собой сумму обратных частот, n1

именно редкие виды: M1-2 . Исполь-i 1 pi зуя соотношение (4) можно получить весь спектр обобщенных размерностей Dq q                         -          .

достигается лишь в случае равно представ-ленности видов.

Таким образом, обобщенные размерности практически не зависят от численности со-общества и являются своеобразными струк-турными инвариантами однотипных систем отличающихся друг от друга размерами .В отличие от них, часто используемые индек-сы Симпсона ( C , 1/C ) и Шеннона ( H ) зависят и от численности,                 :

1/ C N^{D 2} S^{D 2} / D 0 и

H D ₁ ln N D ₁ ln S/ D 0 .

Следовательно, сами по себе они не мо-гут охарактеризовать разнообразия всего со-общества в целом и требуют дополнительного нормирования. Так, например, нормировав индекс Шеннона на его максимальное значе-ние для данного числа видов, получим ин-деке выравненности Пиелу [19], который уже не зависит от числа видов и инвариантен :

H   D 1

E .

ln S D ₀

В случае с индексом видового разнообра-зия Симпсона 1/C , нормирование его лога-рифма на логарифм числа видов дает новый индекс разнообразия у , который также явля-:

ln (¹/ ^C L D 2 D 2

а =------=E .

ln S D ₁ D ₀

Обобщенную размерность D₂ называют в теории фракталов корреляционной размерно-стью , поэтому индекс разнообразияу можно назвать корреляционным инвариантом. За-метим, что каноническая форма индекса вы-

равненности Симпсона

1 CS

инвариантом

:

1 CS

ND 2 S

N D 2 k . Непосред-

ственной проверкой легко убедиться в том, что каждый из всего бесконечного множества инвариантов вида Dq / D 0 представляет со ^-бой индекс выравненное™ и меняется в пре-делах от нуля (для хемостата) до единицы (в случае равнопредставленности видов). Заме-ТИМ, что индекс Маргалефа k (впрочем, каки все обобщенные размерности Dq) достигает единицы только при S = N . Показано, что известные в экологической литературе индек-сы разнообразия (Симпсона, Шеннона, Мар -галефа, Животовского), следует рассматри-вать как частные случаи обобщенных размер-ностей Реньи , лежащих в основе построения

мультифрактального спектра. Обоснована возможность рассмотрения биологического сообщества как мультифрактального объекта и характеристики его спектром размерностей . При таком подходе сообщество рассматрива-стоя как множество, состоящее из отдельных фрактальных подмножеств, которые можно интерпретировать как совокупности особей, относящихся к видам со сходной представ-ленностью. Для таких подмножеств можно вычислить фрактальную размерность D_q , ко -торая и характеризует видовое разнообразие в соответствующей группе видов . Математи-ческий аппарат фрактального формализма позволяет получить весь спектр обобщенных размерностей Dq          q в интервале от

-              . ^q

Характерный вид зависимости D_q(q) пред-ставлен на рис. 2 для четырех отборов проб макрозообентоса в вегетационном периоде 2000 г.      , что функция D_q(q) является не

q возрастающей:     D 1 D0 D1 D2 ... Ра- венство достигается лишь в случае равно представленности видов.

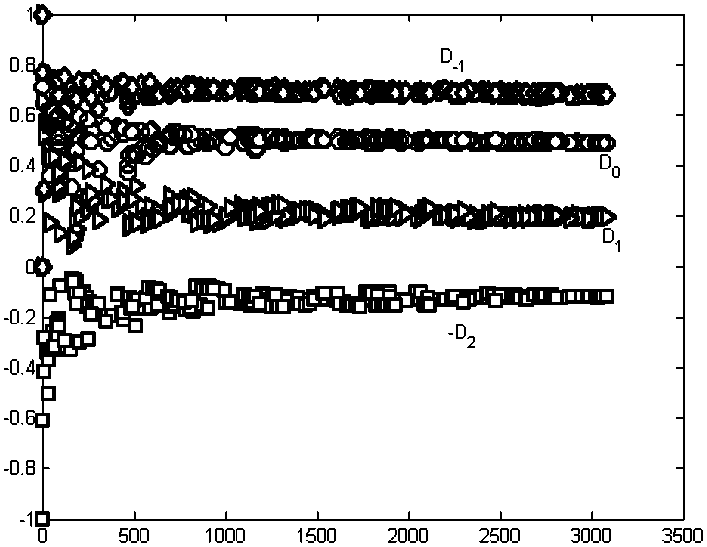
Рис. 2. Вычисление значений обобщенных размерностей Реньи по асимптотическому поведению моментов распределения особей макрозообентоса городских озер по видам при увеличении численности N пробных выборок. По оси абсцисс отложена численность выборок N , по оси ординат - значения моментов.

Моменты порядка: q = -1; О - q = 0; А - q = 1; D -q = 2

Таким образом, обобщенные размерности практически не зависят от численности со-общества и являются своеобразными струк-турными инвариантами однотипных систем отличающихся друг от друга размерами. Итак, обобщенные фрактальные размерно-сти, являющиеся инструментом мульти-фрактального анализа, отражают струк-турную гетерогенность сообщества, обус-ловленную различной представленностью, входящих в его состав видов.

Мультифрактальный формализм

Обсуждаемые выше обобщенные размер-ности Реньи не являются, строго говоря, фрактальными размерностями в общеприня-том понимании этого слова. Поэтому наряду с ними используется так называемая функция мультифрактального спектра f(a) .

Перейдем от переменных q и т( q ) к но-вым переменным с помощью преобразования :

^a(^q) = d^d "Л^q) dq .

f '(^a(^q )) = qa (^q )+Д ^q)

Переменная a («индекс сингулярности») и неотрицательная функция f(a) («спектр син-гулярностей») дают представление о мульти-фрактальности структуры сообщества, полно-стью эквивалентное представлению через q и т( q ). На рис . 3 показана эволюция мульти-фрактальных спектров видового распределе-ния макрозообентоса городских озер Нижне-го Новгорода в период с мая по август 2000 . Экстремум спектра f max ^f(a(q 0)) = k со-впадает с индексом разнообразия Маргалефа и соответствует монофрактальной размерно-сти распределения. Правые ветви кривых на рис . 3 соответствуют отрицательным q . Они систематически короче левых. Такой вид спек-тров объясняется вкладом в сумму в выраже-НИИ (2)                                       :

при больших отрицательных величинах по-рядка момента их вклад становится опреде-ляющим, подавляя влияние других элемен-товструктуры .

В случае равнопредставленности видов спектральная функция f(a) стягивается в точ-ку ,                           f(a) = a .

Существует еще одна характерная точка d fa = 1 aH=a(q=1) кривой f(a): da f a 1, в ко -a aH торой прямая, проведенная через начало ко-ординат под углом 45° к положительному на-правлению оси a, касается кривой f(a). В этой точке значения индекса сингулярности и спектральной функции равны друг другу и совпадают с индексом D1 H /lnN:

f '(a_H ) = a_H ln N . На рис . 2и3 обсужда-емые точки отмечены треугольниками.

Индекс сингулярности a характеризует асимптотическое поведение подмножества видов с фрактальной размерностью f(a) при увеличении численности.              , насколько быстро убывает удельное число представителей данного вида при увеличе-нии суммарной численности N: pi (N)х Nai.

Чем меньше ai, тем медленнее это убыва-ние и тем более представительный вид мы имеем . Размерность f(a) показывает,       - го видов с данной сингулярностью ai содер-жится внутри всего сообщества. Иными ело-вами, f(a) есть размерность подмножества видов с сингулярностью a.

Таким образом, видовая структура биоти-ческих сообществ может быть количествен-но описана с помощью мультифрактального формализма. В свою очередь, график мульти-фрактального спектра (спектра сингулярно-сшей) есть геометрическое место точек, со -

-щепных фрактальных размерностей, вклю -чаюгцих, в качестве нормированных эквива-лентов, все известные показатели видовой структуры сообщества.

Мультифрактальный формализм представ-ляется серьезным инструментом при иссле-довании временнуй динамики видовой структуры биоценозов . Примером может слу-жить анализ зоопланктоценозов Чебоксарс-кого водохранилища. Характерными особен-

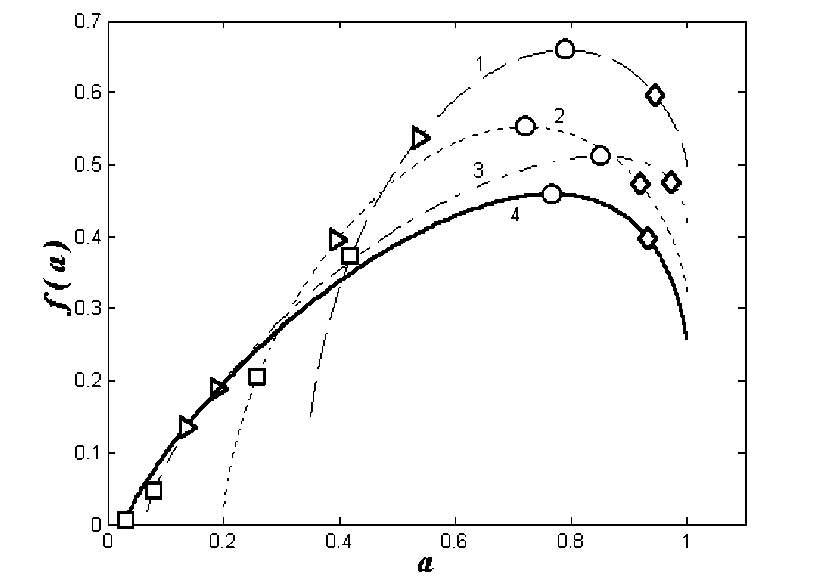
Рис. 3. Сезонная динамика мультифрактальных спектров видовой структуры сообщества макрозообентоса городских озер. По оси абсцисс: a - индекс сингулярности;

ординат: f(a) - спектр сингулярностей.                                          :

1 - в мае, 2 - июне, 3 - июле, 4 - августе.