Элементы компьютерной оптики для коррекции аберраций изображающих систем
Автор: Голуб М.А., Сисакян И.Н., Сойфер В.А.
Журнал: Компьютерная оптика @computer-optics
Рубрика: Элементы компьютерной оптики для коррекции оптических систем
Статья в выпуске: 3, 1988 года.
Бесплатный доступ
Рассмотрен расчет плоских элементов компьютерной оптики, коррегирующих аберрации линз или объективов. В приближении геометрической оптики получено уравнение для фазовой функции корректора. С учетом дифракционных явлений произведены оценки числа Штреля, разрешения и среднеквадратичной аберрации синтезированного корректора, имеющего конечное число отсчетов и уровней квантования фазы. Приведены численные оценки эффективности коррекции аберраций тонкой линзы при применении элементов компьютерной оптики.
Короткий адрес: https://sciup.org/14058142
IDR: 14058142
Текст научной статьи Элементы компьютерной оптики для коррекции аберраций изображающих систем
ЭЛЕМЕНТЫ КОМПЬЮТЕРНОЙ ОПТИКИДЛЯ КОРРЕКЦИИ АБЕРРАЦИЙ ИЗОБРАЖАЮЩИХ СИСТЕМ
Существенное расширение возможностей коррекции сферической и полевых аберраций объективов дают оптические системы с фазовыми слоями [1, 2]. Однако нане сение фазовых слоев по зонам с требуемым рельефом до последнего времени наталкивалось на значительные сложности, преодолеваемые с появлением современной технологии компьютерной оптики для синтеза корректоров волновых фронтов [з]. Возможности изготовления осесимметричных голографических оптических элементов рассмотрены в работах [4, 5]. В данной работе для, вообще говоря, неосесимметричных корректоров рассматривается влияние дискретизации и квантования фазы корректора на качество формирования изображения. В качестве примера приведены оценки числа Штреля и разрешения синтезированного корректора аберраций одиночной линзы. Для упрощения формул расчеты проводятся в случае бесконечно удаленного объекта.
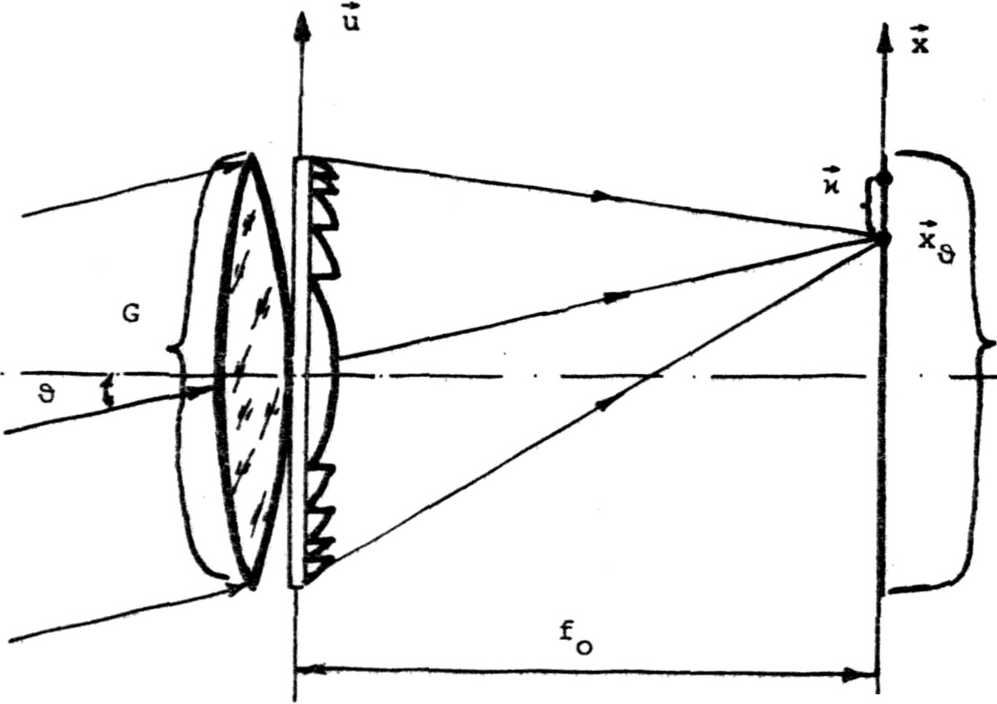
1. Пусть некоторый тонкий кости u=(u, v), а изображение
оптический элемент установлен в области G плос-формируется в области D плоскости х= (х, у), от
стоящей на расстояние fQ.
Введем угловые координаты
О =sinO , О =sinSo, X 1 у 2 где п/2 - 01, п/2 - $2 - углы
объекта 0= (О , О ) х у
луча с осями и и v соответственно. Обозначим
b(u, 0) функцию пропускания тонкого оптического элемента по эйконалу, т.е.
b(u, 6) дает изменение оптической длины пути луча при прохождении точки и под
углом 3.
Геометрический центр или гауссово изображение точки 3 бесконечно удаленного предмета находится в точке
^=R03'
где
R9=f0/VCF(3)
- радиус опорной сферы Гаусса.
Используя уравнение эйконала [б], нетрудно получить для вектора поперечной аберрации соотношение
, _ _ НЬ(“' ®)(4)
и(и, 3)=и - х + f0 . ■ ■ ^ —■ ,
-
9 vi-[$+vub(u, 5))]2
гяе V (fc ' k>*
Волновая аберрация, как известно [б, 7], восстанавливается по формуле
В(и, 3) = В + =- / x(u’, 5)du',(5)
где интеграл берется по любой кривой, проходящей через точки uq и и.
Легко видеть, что в параксиальном приближении, когда 5-0, /?иЬ/«1, имеем:
x(u, О)-u + f0Vub(u, 5),(6)
то есть^
В(и, 5) = во + ^- + b(u, 5).(7)
Таким образом, параксиальная волновая аберрация тонкого элемента совпадает с функцией пропускания b(u, О) этого оптического элемента по эйконалу, из которой вычтена функция пропускания (-u3/2f0) параксиальной линзы.
-
2. Пусть тонкий оптический элемент состоит из тонкого объектива с фокусным расстоянием f (например, одиночная линза или склейка), состыкованного вплотную с синтезированным корректором (см. рисунок). Если bn(u, 3) - волновая аберрация объектива, то для волновой аберрации корректора в^(и, 5) получим уравнение
Bk(u, 5) = ~Ьл(и, д), (8)
где аппроксимация понимается обычно как равенство при некотором 5 для всех и.
В приближении теории аберраций третьего порядка функция В^^/ $) №я осесимметричных оптических систем светового диаметра 2а может быть записана в виде [б]:
В. (и, 3) = Ь. + тВ(—)а + C(f-)2 + fo^^ - Е^ (^- - Е-^)и-,(9)
К КО 4 2 ао 2 д2_2 <хЗ_ а m V а о ао а mmm где В, С, D, Е, F - аберрационные коэффициенты, соответствующие сферической аберрации, астигматизму, кривизне поля, дисперсии, коме; 20^ - максимальный угол поля зрения.
При применении методов компьютерной оптики корректор характеризуется дискретной структурой с N1 х ка отсчетами, разрешением
6, - и®’ ^ " 57 1101
1 2
и числом ш0 двоичных разрядов, используемых для кодирования одного отсчета. При этом пропускание корректора по эйконалу имеет М=21И° градаций. Дискретизация по аргументам и квантование по уровням являются для синтезированных корректоров специфичными принципиально неустранимыми эффектами, определяющими их предельные характеристики. л _ _
-
3. В силу отличия реальной волновой аберрации корректора В^(и, о) от требуемой согласно уравнению (8) система из объектива и синтезированного корректора является не полностью скоррегированной и имеет остаточную аберрацию:
В(и, 3) = 6k(u, 3) - Bk(u, 3) . (11)
При этом функция рассеяния точки (ФРТ) меняет свой вид по сравнению с ФРТ идеальной безаберрационной системы. В частности, интенсивность I в центре х^ кружка рассеяния становится меньше в
ш
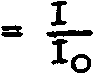
раз интенсивности
1О = /Ео/а -^- (13)
Aafo безаберрационной системы [б], а размер △ кружка рассеяния по уровню О<0<1 становится больше, чем соответствующее значение
^О Этт до - 2^ - k ‘Г (14)
безаберрационной система (например, ЕОг1 = 2,73; Ео = 0,94). При малых остаточных аберрациях, как известно, [б]:
sm = ехр(-каВа) = 1-каВа, (15)
где В- - среднеквадратичная аберрация.
При этом, приравнивая световой поток, проходящий через кружки рассеяния безаберрационной и рассматриваемой систем получаем д - д° -|- .
В случае параксиального приближения остаточная аберрация является невязкой кусочно-постоянной аппроксимацией и может быть оценена математическими методами 131
Ва - -^- + - //V b (u, 3)/2dau, (17) 12Ма 12 G u л где б * max(6if ба).
Проводя простые, но громоздкие выкладки для случая аберрации третьего порядка, из формул (9) , (17) получим ga = Ла + 6а [е£ + Qa [в(С+О) + 5Еа1 +
12Ма 6аа [8 8а 36-1
m(18)
+ е* ( Da+2DC-2Ca + ЕР) + 81 Е^, .
8* 48® 6
mm
Рассмотрим пример. Корректор аберраций к тонкой плоско-выпуклой линзе с радиусом кривизны Rn и показателем преломления п. Используя формулы для аберрационных коэффициентов тонкой линзы, получим
|_1--- »1 + 4i5±v_ al +
12Ма 6 l32(l-v)4 fa 12(l-v) f^ m
, (2+v)a+l aa где v = - ;
Формулы (12)-(18) и, в частности, формула (19) позволяют связать параметры дискретизации корректора (6 и М), параметры оптической системы (поле зрения S^, относительное отверстие 2a/fQ, фокусное расстояние fQ, X, п) с такими характеристиками качества оптической системы, как угловое разрешение A/fQ и число Штре-ля 5щ. Приведенные в табл. 1, 2 расчетные данные позволяют проследить зависимость характеристик оптической системы с корректором от всех параметров и дать рекомендации по выбору разрешения устройства формирования фотошаблона, а также правильно подобрать количество бинарных масок (М-1), используемых при фотолитографическом изготовлении плоского корректора аберраций. Например, из табл. 1 видно, что для получения углов поля зрения до 30° с угловым разрешением 1,5*
Таблица 2
|
6, мкм |
5 | |
10 |
15 |
25 |
35 |
50 |
|
A/fo |
0,92* |
0,95* |
0,99' |
1,17* |
1,48* |
2,48* |
|
SlD _ |
0,93 |
0,88 |
0,79 |
0,58 |
0,36 |
0,13 |
|
Д, мкм |
13,1 |
13,4 |
14,2 |
16,7 |
21,1 |
35,8 |
|
В |
Х/24 |
X/17 |
Х/13 |
X/ 8 |
X/ 6 |
X/4 |
(8т = 30°, 2a/fQ = 1:5, М=8, fQ=SO мм).
Таблица 2
|
м |
2 |
4 |
6 |
|
|
1,38* |
1,04* |
0,97* |
0,95* |
|
|
8 Ш |
0,41 |
0,75 |
0,84 |
0,88 |
|
Д, мкм |
19,9 |
14,9 |
13,8 |
13,5 |
|
В |
Х/1 |
X/ 12 |
Х/15 |
Х/17 —. , , ■ 1 |
(дт = 30°, 2a/fo = 1:5, б = 10 мкм, fQ = 50 мм).
при относительном отверстии 1:5 достаточно обеспечить 6=25 мкм и М=8, что соот ветствует возможностям современной технологии компьютерной оптики. С использованием пакета прикладных программ обработки изображений и цифровой голографии [8] синтезирован плоский корректор аберраций плосковыпуклой линзы с указанными выше параметрами (п=1,6).


