Элементы с высокими значениями первого потенциала ионизации в новом химическом составе фотосферы Солнца

Начало XXI в. в физике Солнца ознаменовалось коренной ревизией сложившихся «классических» представлений о внешних слоях Солнца. Побудительной причиной служит существенный прогресс в технике наблюдений и в методах численного моделирования солнечной плазмы. Появились как наземные, так и внеатмосферные телескопы с чрезвычайно высоким пространственным и временным разрешением; новая вычислительная техника позволяет моделировать внешние слои Солнца от конвективной зоны до короны и солнечного ветра как единый процесс. В частности, прежние одномерные (1D) статические модели отдельных слоев атмосферы – фотосферы, хромосферы – уступают место магнитогидродинамическим трехмерным (3D) моделям конвективной зоны, фотосферы, хромосферы, короны.

Как следствие, нуждается в ревизии одна из фундаментальных проблем физики Солнца – определение его химического состава, поскольку оно выполняется с помощью спектрального анализа фотосферы. Чтобы найти химическое содержание того или иного элемента, необходима очень подробная информация о термодинамических и динамических особенностях среды, ответственной за возникновение каждой конкретной спектральной линии, а также о вероятностях переходов между энергетическими уровнями атомов и ионов данного элемента. По мере уточнения данных атомной физики с одной стороны и усовершенствования методики построения моделей фотосферы – с другой пересматривается интерпретация измеренных эквивалентных ширин линий или их контуров (впрочем, и измерения становятся все более надежными и разнообразными). Появилось множество публикаций с новыми сведениями о содержаниях разных элементов, и вместе с тем общее повышение точности постепенно приводит к сближению результатов отдельных публикаций между собой. Тем не менее, сводные данные о химическом составе Солнца, опубликованные в виде справочных таблиц, нельзя еще считать достаточно надежными. Это обостряет интерес к данной проблеме как солнечных физиков, так астрофизиков (в связи с особой ролью Солнца как звезды-репера в астрофизике в целом).

Наиболее известное событие, связанное с ревизией свойств внешних слоев Солнца, – это опубликование Асплундом в 2005 г. новых данных о химическом составе фотосферы; в 2009 г. Асплунд и др. [Asplund et al., 2009] опубликовали новую справочную таблицу химического состава, в которой подытожили многолетние исследования своей группы. Химические содержания таких обильных элементов, как C, N, O и Ne, уменьшились по сравнению с данными общепринятой ранее справочной таблицы Гревессе и Саувала [Grevesse, Sauval, 1998] 1998 г. В целом изменилась такая важная глобальная характеристика Солнца, как его металличность (Z=0.0134 вместо рекомендуемого прежде значения 0.02). Это повлекло за собой существенное изменение непрозрачности в основании конвективной зоны, что противоречит данным гелиосейсмологии и, в свою очередь, требует пересмотра стандартной модели внутреннего строения Солнца. Реакция научного сообщества на сложившуюся ситуацию, названную даже «кислородным кризисом», неоднозначна; оживленные дебаты продолжаются до сих пор. В дебатах можно проследить две линии:

• 1)    некоторые исследователи, принимая новую рекомендуемую металличность Солнца, пытаются найти не учтенные еще эффекты в теории внутрен-

• него строения звезд, которые привели бы к согласию с данными гелиосейсмологии;

• 2)    другие исследователи, внимательно изучая источники погрешностей при определении химического содержания наиболее обильных металлов, считают преждевременной попытку ревизии стандартной модели.

В настоящем сообщении, не вдаваясь в подробности определения конкретных содержаний элементов, входящих в справочные таблицы [Asplund et al., 2009; Grevesse, Sauval, 1998] (эти детали исчерпывающе обсуждены в многочисленных оригинальных статьях, на базе которых составлены таблицы), мы ставим своей целью анализ статистической достоверности численного различия между данными обеих таблиц, обращая при этом большое внимание на индивидуальные особенности некоторых отдельных химических элементов.

Анализируемые данные

В третьей колонке табл. 1 мы приводим химическое содержание элементов, общих для справочных таблиц в работах [Grevesse, Sauval, 1998; Asplund et al., 2009]:

a el = log — +12, nH где nel – полная концентрация атомов данного элемента, nH – полная концентрация атомов водорода, причем принято nH=12. Эти данные получены Асп-лундом и др. [Asplund et al., 2009] по 3D-модели атмосферы. Они отличаются от принятых ранее справочных значений Гревессе и Саувала [Grevesse, Sauval, 1998], полученных по 1D-модели, на величину

A = aei(3D) - aei(1 D), которую мы подвергаем статистическому анализу. Так как величины Δ существенно неравноточны, то мы придаем им вес w, равный обратной величине от суммы стандартных отклонений ael(3D) и ael(1D). В табл. 1, кроме того, приведены атомные номера A и значения первого потенциала ионизации (FIP) каждого элемента [Аллен, 1977]. В данную таблицу не включены те элементы, для которых стандартное отклонение величины Δ превышает 0.30 (максимальное стандартное отклонение ael(3D) в [Asplund et al., 2009]), а также те элементы, для которых в [Аллен, 1977] не приведены значения FIP.

Статистический анализ различий между со держаниями химических элементов в справоч ных таблицах [Asplund et al., 2009] (3D) и [Grevesse, Sauval, 1998] (1D)

Мы полагаем, что прежде чем обсуждать столь серьезное утверждение о необходимости пересмотра металличности солнечной плазмы, надо проверить статистическую значимость выявленных в [Asplund et al., 2009] различий с прежними их значениями в [Grevesse, Sauval, 1998]. Средняя разность между величинами ael(3D) и ael(1D) в выборке объемом n=51 равна A = -0.039 со стандартным отклонением s=0.065. Рассматривается нуль-гипотеза, состоящая в том, что отличие выборочного среднего A от заданного генерального среднего µ0 (в данном слу- чае µ0(Δ)=0) статистически достоверно. Она должна быть принята на 95-м % уровне значимости, поскольку

I А-^о|

статистика t = J-----1 Vn = 4.256 больше критиче- s ского значения t50;0.05=2.009 [Закс, 1976]. Таким образом, разности Δ на высоком уровне значимости не являются случайными величинами. В своем большинстве они отрицательны, так что уменьшение металличности Солнца, рекомендуемой Асплундом и др. [Asplund et al., 2009], действительно статистически достоверно на уровне значимости выше 95 %.

Естественно, максимальные усилия исследователей направлены на уточнение содержаний самых обильных (после Н и Не) элементов, каковыми являются C, N, O и Ne. Это тем более естественно, что наибольшие различия между данными [Asplund et al., 2009] и [Grevesse, Sauval, 1998] оказались именно у этих элементов. Между тем, содержание ряда элементов, например железа, приведенное в [Asplund et al., 2009] и [Grevesse, Sauval, 1998], не изменилось; есть также элементы, у которых новое содержание больше прежнего. Наше внимание привлекло то, что перечисленные выше элементы обладают двумя особыми свойствами: они самые легкие из обильных элементов и у них высокий первый потенциал ионизации (FIP). По-видимому, те же обстоятельства имеют в виду Каффо и др. [Caffau et al., 2010], отметив, что изучение другой важной проблемы – эффектов диффузии вещества в корону и солнечный ветер – «требует использования точных фотосферных солнечных содержаний некоторых элементов в качестве реперов». C, N, O и Ne в фотосфере практически нейтральны, тогда как железо и большинство других элементов в окрестностях железного пика частично ионизованы. Этот факт служит причиной различной скорости диффузии плазмы из фотосферы в корону (FIP-эффект). При исследованиях FIP-эффекта на Солнце и звездах их фотосфер-ный химический состав служит репером.

Поэтому следующим пунктом нашего анализа является проверка статистической достоверности того, что различия между содержаниями элементов в справочных таблицах [Asplund et al., 2009] и [Grevesse, Sauval, 1998] зависят от FIP и/или от их атомного веса (атомного номера A).

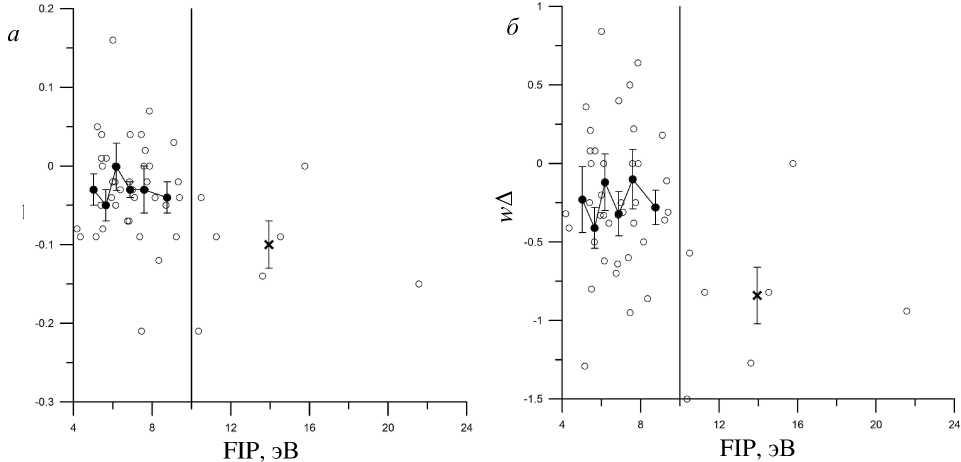
На рис. 1, а показаны величины Δ как функция FIP для всех элементов, вошедших в табл. 1, рис. 1, б показывает то же самое, но для взвешенных значений Δ, т. е. для w Δ. Вертикальная прямая линия при FIP=10 эВ обозначает общепринятую границу между «low FIP»- и «high FIP»-элементами, принятую исследователями FIP-эффекта в короне. Разобьем полную выборку значений w Δ на две выборки и проверим нуль-гипотезу: принадлежат ли выборка low FIP-элементов и выборка high FIP-элементов одной и той же генеральной совокупности? Большинство общепринятых тестов предполагает, что выборки распределены по известному теоретическому закону, чаще всего – по нормальному. К сожалению, выборка high FIP-элементов имеет очень малый объем, следовательно, судить о нормальном или любом другом известном распределении невозможно. Поэтому мы прибегаем к проверке нуль-гипотезы непараметрическим методом Колмогорова–Смирнова,

Таблица 1

A	Элемент	a el [Asplund et al., 2009]	Δ	w Δ	FIP, эВ		A	Элемент	a el [Asplund et al., 2009]	Δ	w Δ	FIP, эВ
3	Li	1.05	–0.05	–0.25	5.39		37	Rb	2.52	–0.08	–0.32	4.18
4	Be	1.38	–0.02	–0.11	9.32		38	Sr	2.87	–0.10	–0.71	5.69
6	C	8.43	–0.09	–0.82	11.26		39	Y	2.21	–0.03	–0.38	6.60
7	N	7.93	–0.09	–0.82	14.54		40	Zr	2.58	–0.02	–0.33	6.95
8	O	8.69	–0.14	–1.27	13.61		41	Nb	1.46	0.04	0.40	6.77
10	Ne	7.93	–0.15	–0.93	21.56		42	Mo	1.88	–0.04	–0.31	7.18
11	Na	6.24	–0.09	–1.29	5.14		44	Ru	1.75	–0.09	–0.60	7.50
12	Mg	7.60	0.02	0.22	7.64		45	Rh	0.91	–0.21	–0.95	7.70
13	Al	6.45	–0.02	–0.20	5.98		46	Pd	1.57	–0.12	–0.86	8.33
14	Si	7.51	–0.04	–0.50	8.15		47	Ag	0.94	0	0	7.57
15	P	5.41	–0.04	–0.57	10.55		56	Ba	2.18	0.05	0.36	5.21
16	S	7.12	–0.21	–1.49	10.36		57	La	1.10	–0.07	–0.64	5.61
18	Ar	6.40	0	0	15.76		58	Ce	1.58	0	0	6.30
19	K	5.03	–0.09	–0.40	4.34		Pr	0.72	0.72	0.01	0.08	6.76
20	Ca	6.34	–0.02	–0.33	6.11		60	Nd	1.42	–0.08	–0.80	6.30
21	Sc	3.15	–0.02	–0.14	6.56		62	Sm	0.96	–0.05	–0.50	5.70
22	Ti	4.95	–0.07	–0.64	6.83		63	Eu	0.52	0.01	0.08	5.67
23	V	3.93	–0.07	–0.70	6.74		64	Gd	1.07	–0.05	–0.62	6.16
24	Cr	5.64	–0.03	–0.43	6.76		66	Dy	1.10	–0.04	–0.33	6.80
25	Mn	5.43	0.04	0.50	7.43		71	Lu	0.10	0.04	0.21	5.00
26	Fe	7.50	0	0	7.90		72	Hf	0.85	–0.03	–0.25	5.50
27	Co	4.99	0.07	0.64	7.86		76	Os	1.40	–0.05	–0.28	8.70
28	Ni	6.22	–0.03	–0.38	7.63		77	Ir	1.38	0.03	0.18	9.20
29	Cu	4.19	–0.02	–0.25	7.72		79	Au	0.92	–0.09	–0.36	9.22
30	Zn	4.56	–0.04	–0.31	9.39		81	Tl	0.90	0	0	6.11
31	Ga	3.04	0.14	0.74	6.00

Рис . 1. Разности между химическими содержаниями элементов , вычисленными на основе табл . 1 в работах [Asplund et al., 2009] и [Grevesse, Sauval, 1998], в зависимости от первого потенциала ионизации . Светлые кружки – отдельные элемен ты ; темные кружки – средние значения по семи или восьми low FIP- элементам ; крест – среднее значение по high FIP- элементам . Бары ошибок – стандартные отклонения от среднего значения ( а ). То же для взвешенных значений разностей ( б ).

Различие химического состава фотосферы по данным 1D- и 3D-моделирования

V

при котором закон распределения не играет роли. В этом методе при сравнении двух выборок 1 и 2 объемами n и m соответственно статистикой является наблюдаемая максимальная абсолютная разность относительных накопленных частот:

D = max

F n

n

^^^^e

F

m

m

n >  m

[Закс, 1976]. Если величина D достигает или превосходит табличное критическое значение статистики D nm при заданной вероятности ошибки α, то нуль-гипотеза должна быть отвергнута, т. е . существует реальное различие между сравниваемыми выборками. Величины D_nm приведены в таблицах [Большев, Смирнов, 1983] для n ≥ m . В нашем случае выборка high FIP-элементов объемом m =7 и с накопленными частотами F_m подлежит сравнению с выборкой low FIP-элементов, объем которой n и накопленные частоты F_n . При этом возможны варианты в том смысле, считать ли выборкой low FIP все имеющиеся в ней элементы или разбить группу на несколько подгрупп с числом элементов, близким m ? Мы рассмотрели несколько вариантов, причем по техническим причинам выбрали n ≤20. В табл. 2 приведены результаты сравнения значений w Δ для ряда отдельных подгрупп low FIP-элементов. В последней колонке приведены вероятности ошибок α, при которых нуль-гипотеза должна быть отвергнута на уровне значимости (1–α) %.

Таблица 2

Результаты сравнения разных выборок low FIP-элементов с выборкой high FIP-элементов (FIP>10 эВ)

Диапазон FIP, эВ	n	m	α
4.18–5.63	11	7	5 %
5.67–6.74	11	7	2 %
6.77–7.64	11	7	5 %
7.65–9.39	11	7	1 %
4.18–5.99	15	7	5 %
6.00–7.44	15	7	1 %
7.46–9.39	14	7	2 %
4.18–6.74	20	7	1 %
6.77–9.39	20	7	1.5 %
4 подгруппы в диапазоне 4.18–7.10	7	7	Всюду 10 %
2 подгруппы: 7.37–7.86 и 7.87–9.39	8	7	10 % и 3.5 % соответственно

случае уровень значимости не превышает 90 %. Таким образом, критерий Колмогорова–Смирнова, действующий более строго, чем простое визуальное сравнение двух выборок, дает основания подозревать, что при учете неравноточности измеренных разностей между содержаниями элементов в двух сводных таблицах, несмотря на очень большую дисперсию этих разностей, на уровне значимости не ниже 90 % имеются систематические различия, связанные с определенными особенностями элемента.

Тем не менее, пока еще нельзя с полной уверенностью утверждать, что именно значения FIP служат причиной различия выборок 1 и 2 в рассматриваемом нами ансамбле элементов. Элементы C, N, O и Ne отличаются от других не только своими высокими потенциалами ионизации, но и тем, что у них малые атомные веса. Может быть, именно легкость этих атомов делает их содержания чувствительными, например, к процессам диффузии в динамически неоднородной среде, где образуются соответствующие спектральные линии? Чтобы ответить на этот вопрос, мы рассмотрели также распределение величин w Δ в зависимости от атомного номера A (рис. 2).

В отличие от рис. 1, а и б , на рис. 2 нет естественной границы, отделяющей одни элементы («легкие») от других («тяжелых»). Поэтому мы произвольно выделили группу из десяти легких элементов (атомные номера 3–14, m =10) и сравнили с этой выборкой четыре оставшиеся выборки примерно того же объема ( n =10). Кроме того, мы сравнили между собой выборки 20 более легких и 20 более тяжелых элементов. Во всех этих случаях критерий Колмогорова–Смирнова дает α>10 %, так что нуль-гипотезу нельзя отвергнуть и, следовательно, нет явной зависимости величин w Δ от атомного номера (и атомного веса) элемента.

Таблица показывает, что, действительно, учет неоднородностей фотосферы (3D-моделирование) по-разному отражается на содержаниях элементов с низкими и высокими первыми потенциалами ионизации. Различия проявляются на высоком уровне значимости независимо от способа разбиения полной выборки low FIP-элементов на подгруппы, кроме случая, когда полная выборка low FIP разбита на мелкие выборки равного объема ( n =7 и 8). В этом

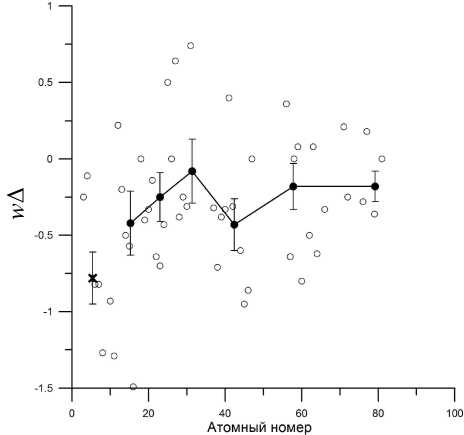
Рис . 2. Взвешенные значения разностей между хими ческими содержаниями элементов , вычисленными на ос нове табл . 1 в работах [Asplund et al., 2009] и [Grevesse, Sauval, 1998], в зависимости от атомного номера . Светлые кружки – отдельные элементы ; темные кружки – средние значения по семи или восьми « тяжелым » элементам ; крест – среднее значение по « легким » элементам . Бары ошибок – стандартные отклонения от среднего значения .

Обсуждение результатов статистического анализа

Как упоминалось во введении, в последние годы обострился интерес к химическому составу Солнца. Появилось множество работ как по уточнению содержаний отдельных элементов, так и с более или менее обширными сводными таблицами значений a el . Мы обсуждаем только справочные таблицы [Grevesse, Sauval, 1998; Asplund et al., 2009], потому что первая из них использована при построении стандартной модели Солнца, а вторая – подытоживает те данные, которые вызвали оживленную дискуссию о точности стандартной модели. По способу моделирования при цитировании таблиц [Grevesse, Sauval, 1998; Asplund et al., 2009] часто используются термины «3D» и «1D» соответственно.

Побудительная причина перехода от одномерного моделирования атмосферы Солнца к трехмерному моделированию состояла в необходимости учета температурных неоднородностей (грануляция). Достоинством 3D-моделей является также отказ от использования таких спорных параметров, как микро-и макротурбулентность; они заменены реалистической привязкой пространственных неоднородностей поля фотосферных скоростей к модели конвективной зоны, порождающей эти неоднородности. Однако, кроме этого свойства новых моделей, в понятие «3D-модель» обычно включают и учет многих других закономерностей, который стал сейчас доступен для уточнения химического состава. Это учет отклонений от локального термодинамического равновесия (NLTE) даже в фотосфере, привлечение новых данных атомной физики (силы осцилляторов, поперечные сечения столкновительных возбуждений уровней, параметры затухания и т. п.). Влияние перечисленных факторов на величину a _el весьма разнообразно, оно зависит от конкретной спектральной линии, по которой измеряется содержание, и нередко влияние, скажем, точности поперечного сечения столкновений с нейтральным атомом водорода (при расчетах NLTE) намного превышает влияние учета неоднородностей (см., например, [Caffau et al., 2010]).

Каждый конкретный химический элемент дает множество спектральных линий в солнечном спектре, но не все они пригодны для определения ael; тщательный отбор линий – обязательное условие химического анализа фотосферы. Некоторые атомы, приведенные в списках [Grevesse, Sauval, 1998; Asplund et al., 2009], не имеют своих линий в спектре фотосферы (в частности, нейтральные атомы Ne), однако в спектре короны имеется множество спектральных линий ионов Ne и некоторых других благородных газов. К счастью, все эти элементы относятся к типу high FIP-элементов, для которых FIP-смещение отсутствует, т. е. их содержание в короне и фотосфере одно и то же. Авторы работы [Asplund et al., 2009] использовали это обстоятельство. При правильном выборе спектральных линий конкретного элемента и достаточной точности атомных данных найденное содержание элемента не должно зависеть от силы линий, состояния их возбуждения, стадии ионизации, структуры термов и других свойств. Наи- более убедительный аргумент, свидетельствующий о физической разумности результатов [Asplund et al., 2009], состоит в том, что впервые удалось согласовать между собой содержания одного и того же элемента, полученные по линиям разного типа, образующимся на разных уровнях атмосферы: по линиям разрешенных переходов нейтральных атомов, по линиям запрещенных атомов, по линиям ионов, по линиям молекулярных полос (см., например, табл. 2 в [Asplund et al., 2009]). Кроме того, новый состав привел и к лучшему согласию с наблюдениями формы спектральных линий, их доплеровских смещений и изменения линий от центра к краю диска. Как указано в [Nordlund et al., 2009], в целом он лучше прежнего, канонического, состава соответствует современным измерениям содержаний элементов в галактической окрестности Солнца (по ближайшим звездам спектральных классов O и B и в межзвездной среде), хорошо согласуется с представлениями о химической эволюции звезд возраста Солнца. Основанные на новом анализе содержания изотопов ряда элементов совпадают с земными изотопными отношениями.

Остается серьезное противоречие с результатами гелиосейсмологической инверсии спектра p-мод глобальных колебаний Солнца, приводящее к расхождению с теоретическими предсказаниями глубины конвективной зоны и профилей скорости звука в основании конвективной зоны. Такое противоречие особенно тревожно ввиду того, что вычисленная по прежним данным металличность Солнца, использованная для построения стандартной модели Солнца, приводила к отличному взаимному согласию теории внутреннего строения звезд и данных гелиосейсмологии. Перечисление результатов многочисленных работ, в которых исследователи пытаются преодолеть это затруднение, выходит за рамки настоящего сообщения. Надо только отметить, что и сотрудники группы Асплунда, и их оппоненты анализируют все возможные пути разрешения проблемы, связанные как с теорией, так и с наблюдениями.

Возвращаясь к результату данного небольшого исследования, мы формулируем его следующим образом.

Статистический анализ разностей между химическими содержаниями элементов, вычисленных по 1D- и 3D-моделям атмосферы (справочные таблицы [Grevesse, Sauval, 1998; Asplund et al., 2009]), выявил систематическое различие между группами элементов с низкими и высокими первыми потенциалами ионизации. Различие установлено на уровне значимости не ниже 90 %.

Выявленное различие заставляет нас обратиться к FIP-эффекту. FIP-эффект, или фракционирование элементов по признаку нейтрал/ион, наблюдается в верхней атмосфере Солнца и в гелиосфере, но зарождается там, где плазма частично ионизована, т. е. сосуществуют нейтралы и ионы, и где подходящая конфигурация магнитного поля благоприятна для их фракционирования. Такие условия, несомненно, встречаются в хромосфере. Другое место, где плазма частично ионизована, – это глубокая или средняя фотосфера. Современные наблюдения с высоким пространственным разрешением (см., например, Ведемейер-Бём и др. [Wedemeyer-Bőhm et al., 2009], их рис. 16) доказали наличие локальных магнитных полей даже внутри ячеек спокойного Солнца. Однако на этом уровне влияние магнитного поля на процесс фракционирования нуждается в проверке из-за большого значения плазменного β. Тем не менее, Шеминова и Соланки [Sheminova, Solanki, 1999] действительно обнаружили слабые признаки FIP-эффекта в фотосфер-ных магнитных трубках потока.

Мы полагаем, что опубликованные в [Asplund et al., 2009] данные об изменении химического состава Солнца при переходе к 3D-моделированию фотосферы могут быть связаны с неполным учетом некоторых видов диффузионных процессов в самой фотосфере. Мы не обсуждаем возможный их механизм, поскольку еще нет общепринятого механизма FIP-эффекта даже для тех слоев, в которых он ярко проявляется.

Если приведенное выше предположение верно, то новые данные [Asplund et al., 2009] о химическом составе Солнца относятся только к той области нижней атмосферы, в которой образуются используемые при диагностике спектральные линии, и отражают локальные особенности диффузионных процессов именно в этой области. Тогда принятый раньше химический состав Солнца [Grevesse, Sauval, 1998], хорошо согласующийся с данными гелиосейсмологии, не нуждается в серьезной ревизии.

В заключение отметим, что заподозренное нами наличие признаков FIP-эффекта в фотосферных слоях, отчасти подтверждающее результаты Шеминовой и Соланки [Sheminova, Solanki, 1999], представляет самостоятельный интерес для изучения этого интересного явления во внешних атмосферах Солнца и звезд.

Работа поддержана грантом Программы государственной поддержки ведущих научных школ РФ НШ-2258.2008.2 и грантом РФФИ 10-02-00153.