Элементы самоорганизации при диффузии газа в систем нанонеоднородностей

Обычно под самоорганизацией подразумевается самопроизвольное образование устойчивых пространственно-временных структур в первоначально макроскопически однородной среде. Такого рода, явления — не редкость в системах, где одновременно протекают конвективные, диффузионные и химические процессы. Различного рода, колебательные процессы и предельные циклы в гамильтоновых системах и странные аттракторы в системах с диссипацией — типичные проявления самоорганизации. Причина этих явлений — нелинейность уравнений, описывающих динамику системы, и взаимодействие различных процессов, протекающих в пей. Считается, что ничего похожего па. самоорганизацию в системах только с диффузией в принципе быть не может. В этой статье мы приводим контрпример. Будет показано, что результатом процесса, диффузии газа, в системе малых неоднородностей может стать возникновение макроскопических осцилляций концентрации.

Соотношение Эйнштейна-Смолуховского, связывающее средний квадрат удаления диффундирующей от точки старта, молекулы со временем: ^/h x ² i ~ t ¹ / 2, получается в предположении о равновероятности всех траекторий молекулы [1]. Траектории с возвращением (замкнутые петли) и уходящие в бесконечность траектории рассматриваются на. равных основаниях.

Между тем бесконечно длинные траектории более вероятны, чем короткие. Это легко попять па. примере игрального кубика, с бесконечным числом граней. Вероятность выпадения произвольной грани с числом очков от 1 до некоторого конечного k нулевая. Вероятность выпадения грани с числом очков в интервале (k; го) равна единице. Бесконечно длинные траектории — аналог грани, принадлежащей второму интервалу. Аномально высокий статистический вес бесконечно длинных траекторий приводит к т. и. супердиффузии, связанной с полетами Леви [2, 3]. В этом случае показатель степени в соотношении Эйнштейна-Смолуховского становится выше 1 /2.

Бесконечно длинные траектории могут быть реализованы и без ухода, молекулы в бесконечность. Например, траектория содержит одну или несколько замкнутых петель, бескопечпокра.тпо обходимых молекулой. В этом случае возможность супердиффузии становится проблематичной.

Движение по петле обладает еще одной интересной особенностью. Петля на. траектории молекулы может быть пройдена, двумя альтернативными способами — по ходу вращения часовой стрелки и наоборот. Так как набег фазы волновой функции любой частицы, движущейся по замкнутой петле, пулевой, амплитуды обеих способов обхода. петли интерферируют конструктивно совершенно независимо от степени упорядоченности неоднородностей среды, в которой происходит диффузия. Цель статьи — выяснить влияние данных интерференционных поправок па. характер диффузии идеальных молекул в случайной системе малых неоднородностей.

Работа выполнена в рамках проекта 10-03-00511 РФФИ и АВЦП «Развитие потенциала высшей школы».

Интуитивно ясно — к чему все сказанное должно привести. В результате конструктивной интерференции возрастает вероятность петлеобразования на. траектории молекулы. Любая петля — неизбежное возвращение в точку старта. Молекулу неотвратимо «тянет вернуться». Результатом такого процесса, является эффективное замедление диффузии. Вполне вероятно, что дело закончится возникновением макроскопических осцилляций концентрации газа. Именно это мы и хотим показать.

В работе рассматривается диффузия идеальных молекул в системе большого числа, малых сферических частиц, случайным образом расположенных в пространстве, или в системе малых сферических включений в однородной среде. Предложенный формализм позволяет рассматривать обе эти задачи с единых позиций. Прилипанием молекул к границам неоднородностей пренебрегается. Эффективный коэффициент диффузии вычисляется методами теории многократного рассеяния из анализа, усредненной функции Грина, диффузионного уравнения. При этом мы выходим за. рамки классического приближения когерентного потенциала, или приближения эффективной среды [4, 5] и включаем в массовый оператор уравнения Дайсона, последовательность т. н. веерных диаграмм [6-8], описывающих интерференцию амплитуд двух возможных способов прохождения замкнутой петли па. траектории молекулы.

II.    Основные уравнения. Потенциал взаимодействия

Запишем уравнение диффузии для концентрации молекул с (r , t ) в рассматриваемой системе

∂ dt с (г, t) - D оДс (г, t) = 0; с (г, 0) = с о (r), где со (г) — начальная коппситрания и Dо — коэффициент диффузии. В представлении Лапласа, по времени это уравнение выглядит следующим образом:

sc ( г , s ) - D оД с ( г , s ) = с о ( г ) .

Нетрудно видеть, что если функция Грина, или пропагатор является решением уравнения sGо (r, г0) - DоДGо (r, r0) = 5 (r - r0),     (1)

то с (r , s ) может быть представлена следующим образом:

Решение уравнения (1) в однородном пространстве, характеризуемом D _о, хорошо известно:

G о( г , г' ) =

i ^exp^{( -} VD । ^{г - г} 0 1 ) 4 nD о         | г — г 0 |

Наша задача. — осуществление аналогичной программы в системе сферических неоднородностей (включений), плотность которых n ( г )  =

= n^ 6 (R — I ai — г | )■ Злось n — плотность мате-ai риала включений, 6 (x) = 1 внутри сферы радиуса R, 6 (x) = 0 вне ее, ai — радиус-вектор координаты центра, сферы. В дальнейшем мы будем работать с безразмерной плотностью п(г) = n(г)/п.

Пропагатор G 1 в однородной среде с коэффициентом диффузии D 1 отличается от G _о заменой D о л a D 1. но пропс дур>а получения G 1 поможет нам построить пропагатор в системе неоднородностей. Мы хотим представить процесс трансформации G _о в G 1 как результат некоторого эффективного «взаимодействия», которое испытывают молекулы диффундирующего газа, переходя из среды с D _о в среду с D 1. Эта трансформация описывается уравнением Дайсона:

G 1 ( г , г' ) = G о ( г , г' ) +

+ j G о ( г , Г 1) P ( Г 1 , Г 2) G 1 ( Г 2 , г' ) d Г 1 d Г 2 .

Оператор P ( г , г' ) назовем «потенциалом взаимодействия». Его вид легко установить [9]. В представлении Фурье по разности координат уравнение (3) выглядит так:

( s + D i к ²⁾ ’ 1 =

= ( s + D о к ² ) ^- 1 + ( s + D о к ² ) ^- 1 P ( к ) ( s + D i к ² ) ^- 1 .

Следовательно,

P ( k ) = ( D о - D i) к к

И

P ( г , г' ) = j P ( k ) e^{- i k(r} - ^r 0 ) d k =

= ( D о - D i) — 5 ( г - г' ) . (4) ∂r∂r⁰

Теперь для построения пропагатора G в системе неоднородностей нам осталось сделать только один шаг. Перепишем уравнение для G 1 в виде бесконечного ряда:

G i = G о + ( G о PG о) + ( G о PG о PG о) + ..., (М

c

( r , s ) =

G о( г , г 0 ) с о ( г 0 ) d r 0 .

Пусть с _о( г' ) = 5 ( г _о - г' ) — единичный точечный источник, локализованный в точке го- Тогда с ( r , s ) = G о( г , г д). Другими словами. G _о( г , г _о) показывает, какова концентрация молекул в точке г однородного пространства, (ее лаплас-образ), если в точке го в систему ввели одну единственную молекулу.

где скобки обозначают интегрирование по внутренним координатам. Соответствующее уравнение для G напоминает (-5):

G = G о +

G 0^X a

P ^a G 0

+

+ [ G о X P a G о X P b G о) ab

+ . . . (6)

Индексы а, Ь, . .. нумеруют неоднородности и в то же время это — координаты их центров. Мы предполагаем, что усредненный пропагатор G в системе частиц выглядит точно так же, как соответствующий пропагатор в некоторой однородной среде, характеризуемой эффективным коэффициентом диффузии D;

G ( r , r 0 ) =     ~

4 nD

Нахождение D будет основной нашей задачей. В соответствии с таким подходом потенциал взаимодействия P по аналогии с выражением (4) имеет

ВИД

P a ( r , r 0 ) = ( d - D 1) n a ( r )        , 5 ( r - r 0 ) ,    (8)

∂r∂r0

где n a ( r ) = 9 ( R — I a — r I ) D 1 — коэффициент диффузии внутри материала, неоднородности.

мой (т.п. t-ма.трицей), мы окажемся в рамках хорошо известного в теории неупорядоченных систем приближения когерентного потенциала, или приближения эффективной среды [4,5]. Последующие диаграммы для массового оператора, описывают движение молекулы вдоль замкнутой петли. Сумма этих диаграмм выражается через блок P, известный в теории многократного рассеяния, как сумма, т. и. веерных или максимально перекрещенных диаграмм [6-8]. Приведенные диаграммы описывают интерференцию амплитуд, соответствующих двум альтернативным способам обхода, молекулой петли (см. рис. 2). Координаты каждого из пропагаторов в диаграммах для У разделены расстоянием порядка R. В этом случае, если средняя длина, свободного пробега, молекулы А много больше R, мы можем пренебречь экспонентой в числителе фигурирующих в диаграммах для У пропагаторов.

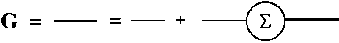
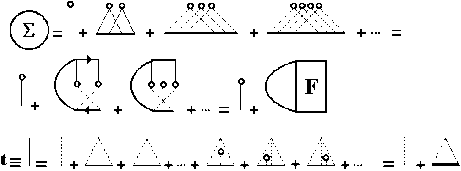
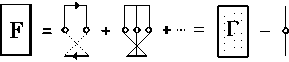
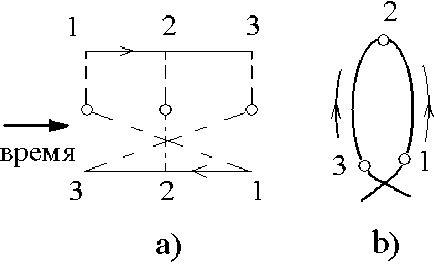
Рис. 2. Характерная диаграмма для блока Г, описывающая интерференцию амплитуд двух способов прохождения молекулой петли на ее траектории

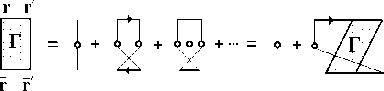
Рис. 1. Система уравнений для усредненного пропагатора

Система, уравнений (рис. 1) выглядит следующим образом:

G ( r , r 0 ) = G o( r , r 0 )+

Усредним уравнение (6) по координатам центров неоднородностей. Структура, ряда, теории возмущений для усредненного пропагатора G показана. на. рис. 1. Жирная горизонтальная линия соответствует G, тонкая — пропагатору G 0, пунктирная линия — «потенциалу взаимодействия» P a . Каждому кружку сопоставляется интегрирование по а и мио житель n 0 / (1 — f ), г де n 0 — концентрация неоднородностей, f — фактор упаковки, или доля всего объема, запятая ими. Появление f в знаменателе отражает ограничения в объеме интегрирования, связанные с собственным объемом неоднородностей.

Структура, приближений, использованных при суммировании ряда теории возмущений для G хорошо понятна, из рис. 1. Если в массовом операторе У ограничиться первой диаграм

+ j — f У G o( r , r i)y( r i , r 2) G ( r 2 , r 0 ) d r i d r 2 , y( r , r 0 ) = i nf У t a ( r , r 0 ) d a +

• + У F ( r , r i , r 2 , r 0 ) G ( r i , r 2) d r i d r 2 ,

F ( r , r 0 , r 0 , r ) = P( r , r 0 , r 0 , r ) —

• — 1 — 1 / t a ( r , r 0 ) t a ( r 0 , r ) d a , P( r , r 0 , r 0 , r ) = i n⁰ f У t a ( r , r 0 ) t a ( r 0 , r ) d a + + i nf / t a ( r , r i) G ( r i , r 2)P( r 2 , r 0 , r 0 , r 2) X x t a ( r 0 , r ₂) G ( r ₂ , r _i) d a d r _i d r ₂ d r ₂ d r _i ,

t a ( r , r 0 ) = P a ( r , r 0 )+

+

J P a ( r , Г 1) G ( r i , Г 2) t a ( r 2 , r' ) d r i d Г 2 . (13)

Сделав замену переменных г — а ^ г, г’ — а ^ ^ г ' , перепишем уравнение (13) в более удобной форме:

t ( г , Г') = P ( г , Г') +

+ 1P ( г , Г 1) G ( Г 1 , Г 2) t ( Г 2 , г' ) d Г 1 d Г 2 . (14)

Его решение ищем в виде, аналогичном (8):

∂ ²

t ^(Г , ^Г) = ^т п ^(r) _дгдГ 0 ^{5 (Г} - ^Г) .        (15)

Посколвку Г1 и г2 находятся внутри неоднородности, экспоненты в пропагаторах, входящих в уравнение (14), можно опуститв. Подставим (15) в уравнение (14) и проинтегрируем по частям. В ре-зулвтате с точноствю до членов, содержащих малый параметр R/Х., нетрудно получитв простое алгебраическое уравнение для т, из которого следует, что т = D( D — D 1)/D 1.

Далее найденную t-матрицу подставляем в уравнения (9) - (12) и ищем решение уравнения для блока веерных диаграмм Г в следующем виде:

∂ ⁴

Г( г , r , r , г ) =       ,_я-,_я- ^ф( г , Г , Г , г ) .

∂r∂r ∂r ∂r

Повторяя действия, исполвзованные при решении уравнения (14), для Г нетрудно получитв следующее выражение:

Г( г , Г , Г ' , Г ).        ^{Т 2}у , ^Г>        x

• ^{1    —} (d) n ^{0 v} T r - f

^x ^ ^{5 (r — Г} ' ) № ^{5 (Г} ' ^{— Г)} ,

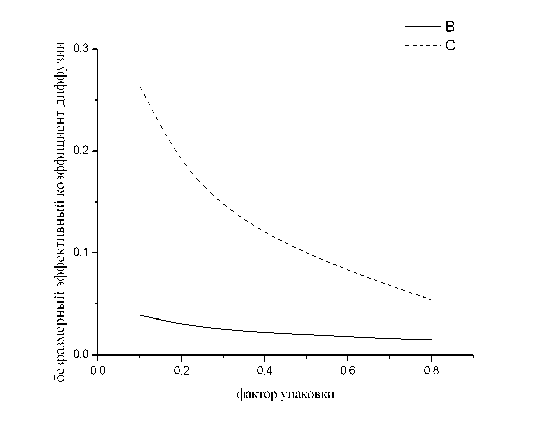
Рис. 3. Кривая В — безразмерный эффективный коэффициент диффузии D/Dо (Dо — коэффициент диффузии газа в окружающем частицы пространстве) в зависимости от фактора упаковки. Отношение D 1 /D0 = 0.01 (D — коэффициент диффузии внутри материала частиц). Кривая С — эффективный коэффициент диффузии, рассчитанный в рамках приближения когерентного потенциала где

• ^ (г — r ' ) = I 0 ( R — | а — г I ) 0 ( R — | а — г ' | ) d а =

= 12 (2 R — | г — г ' | )²(4 R + | г — г ' | )0(2 R — | г — г ' | ) .

Подставив F, связаиное с Г уравнением (11), в выражение для Е, нетрудно убедитвся в локалвности массового оператора. Из-за этого уравнение Дайсона (9) для усредненного пропагатора имеет тот же вид, что и в однородной среде. Из условия са-мосогласования системы уравнений (9) - (13) нетрудно получитв алгебраическое уравнение для D:

• ^{1    —} gU/m + g p /D)

D 0 — D = дт--------- ^{7     V}2 ---L ,   (16)

• ^{1    —} д {/D)

где д = f/ (1 — f ). В рамках приближения когерентного потенциала уравнение намного проще:

( D 0 — D ) /D = д ( D — D 1) /D 1 .

В рамках предлагаемого подхода проблема граничных условий к уравнению диффузии решается доволвно просто. Кроме D ₀ мы задаемся коэффициентом диффузии молекулы в материале неоднородности D 1. Условие D 1 ^ D ₀ соответствует жестким частицам и отражению молекул от их поверхности. Ситуация D 1 ^ D 0, наоборот, описывает «прозрачные» для молекул включения («полости»). Варвируя отношение D 1 /D ₀, можно рассмотретв многие диффузионные процессы в неоднородных средах.

На рис. 3 4 показана зависимости от фактора упаковки эффективного коэффициента диффузии, рассчитанного в рамках обеих приближений как для «жестких» частиц, так и для «полостей». Диффузия с учетом замкнутых траекторий

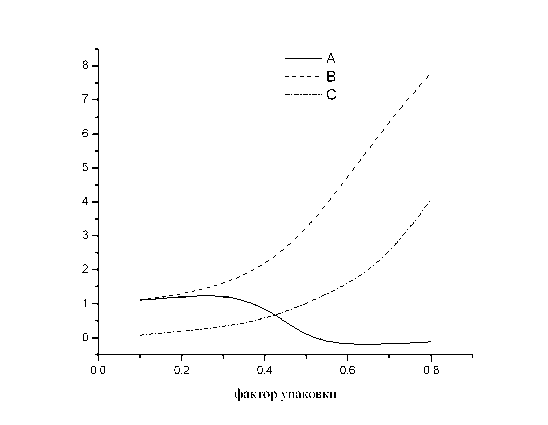
Рис. 4. Кривая А — безразмерный эффективный коэффициент диффузии D/Dо (Dо — коэффициент диффузии газа в окружающем включения пространстве) в зависимости от фактора упаковки. Отношение D 1 /D0 = = 10 (D 1 — коэффициент диффузии внутри материала включений). Кривая В — эффективный коэффициент диффузии, рассчитанный в рамках приближения когерентного потенциала. С — параметр р, сигнализирующий о появлении мнимой части D в случае «жестких» частиц заметно ниже, чем в рамках приближения когерентного потенциала.

где р = д ( D - D Д² /D 1². Эти корни можно представить в виде

III. Макроскопические осцилляции концентрации

В разделе 2, вычисляя У, мы пользовались упрощенным выражением для пропагатора. Отброшенные слагаемые содержали малый параметр R/А, и ими можно было пренебречь. Теперь мы выйдем за. рамки этих приближений. Дело в том, что отброшенные малые поправки имеют мнимую составляющую, что сразу же привносит в задачу новую физику.

Происходит это следующим образом. Если воспользоваться тождеством

⁽ - д + а 2) eXP( = ar 2 = - 4 nS ( r ) ,

у i = 2cos 3 , у 2 = - 2cos Q + П) , y ³ = ^2c„ (3 ^{- П} ) ,

то выражение для У принимает следующую форму:

У( г , Г 0 ) = тд

1 +

(D)

g

(D)

g

∂ ² ∂r∂r⁰

S ( r - r ⁰ ) -

) 2«

S                 ф ²( r , r 0 )

D 1 - ( т/D )²( n о / (1 - f )) ф ( r , r 0 )

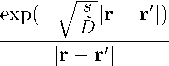
t. e. массовый оператор становится нелокальным. Теперь уравнение для G выглядит следующим образом:

G ( r , r ⁰ ) = G 0 ( r , r ⁰ )+

+ ( т/D)

τg ²

^{1 -} ( ^t/d) д

IG o( r , r i) G ( r i , r 0 ) d r i -

где cos 6 = р ¹ - 1. При р >  1 кореиь у ₂ может попасть внутрь интервала, интегрирования, который в новых переменных становится [0; 1].

Функция ф ( х ) в уравнении (18) обращается в нуль за. пределами неоднородности, в то время как характерные расстояния, на. которых существенно меняются диффузионные пропагаторы, гораздо больше (порядка А ). Поэтому зависимостью от х пропагатора в правой части (18) можно пренебречь.

Расчет показывает, что условие р >  1 в случае «жестких» частиц никогда, не выполняется. В случае мягких включений («полостей») ситуация меняется. На рис. 4 представлена, зависимость р от фактора упаковки для включений с D 1 /D 0 = 10. Как мы видим, при достаточно высоких значениях f в уравнении (18) появляется мнимая часть. Одновременно эффективный коэффициент диффузии обращается в нуль. Другими словами, начиная с этого момента, диффузия прекращается. При еще больших факторах упаковки эффективный коэффициент диффузии становится комплекснозначным. Причем действительная часть этого коэффициента, становится отрицательной (см. рис. 4).

Проще всего оценить мнимую часть D в том случае, когда D близок к нулю. Несложные вычисления позволяют свести уравнение (18) к следующему виду, ничем не отличающемуся от соответствующего уравнения в однородной среде:

G ( r , r 0 ) = G o( r , r 0 )+

_τ                         3 _s

^- _{4 П} ⁽ n о / ^{(1 -} f )) (//D) D ^x

+ тд

x j G о( r , r i)

ф ^{2 (} x )

1 - т/D ( n о / (1 - f )) ф ( x )

x

¹⁺®1 - ⁽ ^ь д

⁺ i 6^{4 п т} д D R ² у 2r ^x

x j G o( r , r i) G ( r i , r 0 ) d r i .

exp ф Д x) x

G ( r _i - x , r 0 ) d r d x .

Нас интересует мнимая часть (18), связанная с обходом расположенного па. действительной оси полюса. подынтегрального выражения во втором интеграле справа. После перехода к переменной у = = х/ 2 R нули его знаменателя содержатся среди корней следующего уравнения:

Для мнимой части эффективного коэффициента, диффузии в рассматриваемом случае нетрудно получить следующее выражение:

Im D = -3- ngsR cos

1 - 2 f      "I arccos —----f + 3 . 1211

у ³ - 3 у + 2 = 2 /р,            (19)

Зависимость этой величины от фактора, упаковки приведена, на. рис. 5.

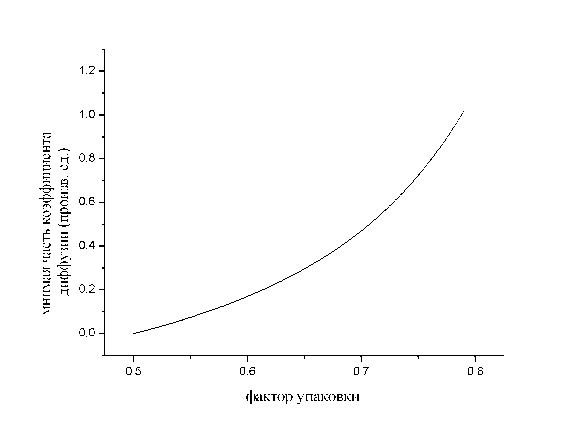
Рис. 5. Зависимость мнимой части эффективного коэффициента диффузии от фактора упаковки

Для интерпретации мнимой добавки к D воспользуемся следующими соображениями. Представим себе, что коэффициент диффузии — чисто мнимая величина: D = iD2. Тогда изменение со временем полного числа молекул внутри произвольного объема, ограниченного замкнутой поверхностью S, определяется уравнением неразрывности dN dt

-

iD 2

I V c • d S = 0 .

S

Удовлетворить ему можно, предположив, что полное число молекул внутри рассматриваемого объема осциллирует со временем с частотой ш;

N гс N0 exp(iшt), где N0 — некоторое среднее число. По такому же закону осциллирует и концентрация молекул:

c гс c о exp( iшt ) .

В результате частота колебаний связана с N 0 и c ₀ соотношением

D 2 R V c ₀ • d S

“ =  ■—     ^т

^^

или ш гс D 2, г де L — характерный размер рассматриваемого объема и l — характерная длина, на которой изменяется концентрация.

Существование отрицательной действительной части D приводит, на первый взгляд, к неограниченному экспоненциальному росту со временем числа осциллирующих молекул. Действительно, если D = D 1 + iD 2, число молекул в рассматриваемом объеме ведет себя со временем следующим образом:

N (t) гс N0 exp(iшt) exp(—5t), где 5 гс D1.

На самом деле это не так. После того как диффузия прекращается, молекулы начинают осциллировать. Число таких молекул не может пре высить число реальных, участвующих в диффузии молекул. Параметр 5 определяет характерное время, за которое происходит процесс локализации молекул. Если бы действительная часть эффективного коэффициента диффузии после того как он стал комплексным была бы положительная, мы бы имели дело с экспоненциальным затуханием осцилляций. Этого в рассматриваемом случае не происходит.

На наш взгляд, после того как D обратится в нуль, эффективный коэффициент диффузии теряет свой первоначальный смысл и начинает описывать совершенно другие процессы — осцилляции концентрации. На первый взгляд, речь идет о высокочастотных микроскопических колебаниях молекул, соответствующих их движению по разномасштабным замкнутым петлям. И действительно, в рассматриваемом случае ( 5 близко к нулю) частота колебаний может быть любой, т. к. в соответствии с выражениями (21) и (22) ш ~ ~ s , где s — лаплас-образ времени. В простейшем случае точечного 5 -образного источника лаплас-образ концентрации c (r , s ) в любой точке пространства тождественен лаплас-образу самой усредненной функции Грина G (r , s ). Последняя выглядит так же, как функция Грина в однородной среде с эффективным коэффициентом диффузии D. Обратный переход от c (r , s ) к c (r , t ) сопряжен с интегрированием вдоль мнимой оси комплексной плоскости s правее корневой точки s = 0. Интеграл сводится к интегралу Пуассона по переменной, пропорциональной ^s . Основной вклад в последний интеграл вносит область малых значений s. Следовательно, концентрация молекул с низкими частотами колебаний подавляюще велика.

Характерная частота ш колебаний определяется размером петли L и тепловой скоростью молекул v. ш ~ v/L поэтому характерные частоты, на первый взгляд, — микроскопические. При L ~ ~ 0 , 1м, v ~ 102 м/с, ш ~ 103 с ~ 1. Однако не следует забывать, что петли обходятся молекулами многократно и «эффективный» характерный размер петель может превосходить L на много порядков. В связи с этим в системе полостей в однородной матрице можно ожидать появления макроскопических осцилляций концентрации газа с вполне макроскопическими периодами.

IV. Заключение

Рассмотренные выше особенности диффузии связаны с замкнутыми петлями на траекториях диффундирующей молекулы. Набег фазы волновой функции любой частицы при обходе замкнутой петли нулевой. Амплитуды двух альтернативных способов прохождения такой петли (по ходу вращения часовой стрелки и наоборот) всегда интерферируют конструктивно независимо от степени упорядоченности среды. Любая петля на траектории — это обязательное возвращение назад. Упомянутая интерференция увеличивает вероятность возвращения. Соответственно увеличивается вероятность петлеобразования. Далее все начинается снова. Возникает своего рода, са-моподдерживающийся процесс, результатом которого является «увязание» молекулы в системе петель и ее эффективный останов или локализация.

Диаграммы уравнения Бете-Солпитера можно рассматривать как описывающие эффективное взаимодействие пары виртуальных молекул, обходящих петлю в двух взаимно противоположных направлениях. Причина такого взаимодействия — рассеяние на. одних и тех же частицах. Можно сказать, что именно это взаимодействие является физической причиной зацикливания молекулы. С подобного рода, взаимодействием сталкиваются в задаче о движении электрона, в случайной системе примесей в решетке. Реальное движение электрона. эквивалентно распространению электрошю-дырочиого возбуждения или виртуальной пары электрон-дырка. Электрон и дырка, перед тем как схлопнуться эффективно взаимодействуют друг с другом, рассеиваясь на. одних и тех же примесях. Рассматриваемое взаимодействие описывается двухэтажными диаграммами, аналогичными нашим. В частности, веерный ряд описывает взаимодействие электрона, и дырки, обходящих замкнутую петлю па. траектории соответственно по ходу вращения часовой стрелки и наоборот. Эти диаграммы, как известно, приводят к аидерсоиов-ской локализации электрона, или к обращению в пуль его коэффициента, диффузии [6-8]. Таким образом, обнаруженное нами замедление и прекращение диффузии — вполне ожидаемое явление. Это есть прямой аналог электронной локализации.

Как только эффективный коэффициент диффузии обращается в пуль, в системе полостей в однородной матрице возникают временные осцилляции концентрации, связанные с движением молекул по замкнутым петлям. Причем основная часть молекул колеблется с низкими частотами, вполне доступными для наблюдения невооруженным гла-

3OM.

Остановку диффузии можно рассматривать как новый механизм физической адсорбции, обладающей довольно странными свойствами — чем хуже «прилипают» молекулы к поверхности неоднородностей, тем выше эффективная адсорбция. Подобного рода, свойства, могут оказаться полезными в создании эффективных накопителей водорода. — главной задаче водородной энергетики.