Элементы статистической концепции обучения нейронной сети и прогнозирование точности ее функционирования

Расширению области приложений методов обработки информации на основе нейронных сетей (НС) как наиболее мощного средства аппроксимации многопараметрических зависимостей (многомерных функций) может способствовать более полное представление о статистических концепциях и принципах обучения НС. Корректно формализованная и логически адекватная основа процесса обучения строится на элементах статистической теории обучения [1-5] и позволяет учитывать вероятностный тип зависимости вход—выход НС, т. е. вероятностный тип зависимости передаточной функции сети, которая связана с ее структурой и величиной синаптических весов [6].

В практической реализации алгоритмов обучения НС особенно трудной остается задача оценки соотношения между доступным размером обучающей выборки, достигнутом при обучении показателем точности работы НС (выполнения желаемого вида многопараметрического отображения) и ожидаемым показателем точности преобразования на данных, не использовавшихся при обучении. Такую проверку нейросети называют тестированием, и показатель качества выполнения требуемого преобразования сетью определяется достигнутой (за счет обучения) способностью НС к обобщению.

Основные понятия, концепции и некоторые аспекты статистической теории обучения рассматриваются применительно к НС с прямым распространением сигнала [6-7], супервизорной ("с учителем") формой обучения и вероятностным представлением как входных данных (векторов x с распределением P(x)), так и выхода НС — вектора у с условным распределением P(y|x).

Супервизором (учителем) выдается сети набор одинаково и независимо распределенных векторов x из распределения P ( x ) с соответствующими значениями выхода у из распределения P ( y | x ). Этим создается обучающая выборка образцов — примеров:

{ x i , y i ; Х 2 , у 2 ; ...; x n , у n }. (1)

Считается, что распределения P ( x ) и P ( y | x ) вполне определенные, но неизвестные, а доступной информацией служит только обучающая вы-борка{ x ₁, y ₁; x ₂, y ₂; ...; x _n , у _n }. Обучаемая НС за счет выбора значений ее параметров (совокупности а синаптических весов из некоторой допустимой области определения Л ) способна выполнять набор функций отображения { f x , a ), а е Л }. Задача обучения состоит в выборе некоторой функции, которая принадлежит множеству { f x , a ), а е Л } и которая предсказывает (наилучшим образом) ответы супервизора. Отбор такой функции основывается на обучающем множестве (1), состоящем из n случайных и независимых, одинаково распределенных (НОР) наблюдений, извлекаемых в соответствии с вероятностью P ( x , у ) = P ( x ) P ( y|x ). Выбор лучшего из доступных приближений к желаемому отображению (т. е. к откликам супервизора) осуществляется минимизацией риска. Это значит, что нужно выполнить три этапа.

• 1.    Найти подходящую меру расхождения (так называемую функцию потерь) L ( у , f x , a )) между откликом супервизора у и откликом, который обеспечивается обучаемой НС.

• 2.    После этого на основе вероятности P ( x , y ) следует получить функционал риска (ФР) в виде ожидаемой функции потерь R ( а )¹ ) :

• 3.    Найти функцию f x , а ₀), которая минимизирует функционал риска R ( а ) по классу функций { / ( x , a ), а е Л } в условиях, где распределение совместной вероятности P ( x , y ) неизвестно и доступна только информация, содержащаяся в обучающем наборе (множестве) (1).

R ( а ) = J [ L ( y , f ( x , a ))]d P ( x , y ). (2)

Рассматриваемая модель обучения НС, принцип минимизации функционала риска, его компоненты и этапы реализации для получения лучшего отображения, аппроксимирующего желаемое отображение (задаваемое супервизором на обучающей выборке), охватывает все основные задачи, которые решаются средствами НС. Это — задачи распознавания образов, оценки нелинейной регрессии и выбора максимально правдоподобной плотности вероятности [8-10].

• •    При бинарном распознавании образов выход y , определяемый супервизором, принимает два значения у = {0, 1}, а { / ( x , a ), а е Л } — это набор функций-индикаторов (т. е. функций, которые принимают только два значения — нуль или единицу). В качестве функции потерь принимается выражение

  L ( у . f ( \ . ^{а ))} =

  
  

  0 , если

  1, если

  
  

  у = f ^{( x} , ^{а )} ; у * f < \ . ^{а )} .

  
  
  
  

Для этой функции потерь функционал (2) обеспечивает вероятность ошибки классификации (т.е. когда ответы у , даваемые супервизором, и ответы, даваемые функцией-индикатором f x , a ), отличаются). Поэтому задача состоит в том, чтобы найти функцию, которая минимизирует вероятность ошибки классификации. При этом мера вероятности P ( x , y ) неизвестна, но имеются обучающие данные (1).

• •    В задаче оценки регрессии ответы супервизора у и набор / x , a ), а еЛ }, который содержит функцию регрессии f x , а ₀), связаны соотношением f ( x , а ₀) = | у d _yP ( x , у ). Причем известно, что для

f x , а ) е L 2 регрессией является функция, которая минимизирует функционал (2) с функцией потерь в форме (4):

^L ( у - f ^{( x} , ^{а ))} = ⁽ у ^- f ^{( x} , ^{а )) 2}.             ⁽⁴⁾

Так что задача оценки регрессии — это задача минимизации функционала риска (2) с функцией потерь (4) в ситуации, где распределение вероятности P ( x , y ) неизвестно, но имеются обучающие данные (1).

• •    В задаче оценки плотности распределения вероятности из набора плотностей {р ( x , a ), а е Л } в качестве функции потерь может использоваться выражение

L ( р ( x , а )) = - log( р ( x , а )). (5)

Желаемая плотность минимизирует функционал (2) с функцией потерь (5). Так что снова, чтобы оценить плотность, исходя из данных (1), нужно минимизировать функционал риска при условии, что распределение вероятности P ( x , y ) неизвестно, а данные ( x 1 , x ₂ ,..., x n ) независимы и одинаково распределены.

Развитие введенных выше исходных представлений о статистической основе обучения позволяет:

• •    ввести понятие эмпирического риска R _эмпир ( а ) в виде среднего (по обучающей выборке) от функции потерь;

• •    ввести формализованное выражение для фактического риска (взвешенной по вероятности функции потерь), который характеризует уровень обобщения НС;

• •    установить правило индукции принципа минимизации эмпирического риска (принципа МЭР), согласно которому при увеличении размера обучающей выборки R _эмпир ( а ) н R ( а ) (эмпирический риск стремится к его фактическому значению [1, 3, 5, 6, 11].

Обоснование справедливости принципа МЭР использует понятие энтропии H(n), характеризующей многообразие набора функций {/(x,a), аеЛ}, и понятие размерности Вапника—Черво-ненкиса, определяющей (для того же набора функций) способность реализовать разделение набора обучающих точек (векторов) дихотомией различного вида 2). В упрощенной формулировке возможность применять правило принципа МЭР определяется условием выполнения соотношения

H ( n )

n

nн^ 0, которое верно при сильном возраста- нии размера обучающей выборки.

Следующим этапом является оценка скорости сходимости R _эмпир ( а ) ^ R ( а ) эмпирического риска к фактической его величине (ожидаемой на фазе тестирования). Такая оценка получается в форме верхней границы возможного различия фактической функции риска от R _эмпир ( а ). Эта граница | R( а ) - R _эмпир ( а ) | зависит от объема обучающей выборки и размерности Вапника—Червоненкиса и может быть определена как для конкретной задачи с фиксированной функцией распределения P ( x , y ), так и в толерантной форме, т. е. в форме границы, которая справедлива при любой функции распределения.

Наличие таких границ позволяет (еще на стадии обучения сети) с помощью размера обучающей выборки и меры сложности набора отображений (характеризуемой РВЧ) влиять (и корректировать) на показатели обобщения НС на стадии ее тестирования, а затем и функционирования [11-14].

Особенно продуктивным оказывается так называемый метод структурной минимизации эмпирического риска в задаче бинарного распознавания образов, в которой используются разделяющие плоскости (или их нелинейные отображения в пространство размерности выше, чем размерность входных векторов). Эти плоскости выбираются по критерию наибольшей величины минимального отстояния от нее разделяемых точек (векторов) обучаемой выборки и называются оптимальными разделяющими плоскостями. Векторы, помещающиеся на границах плоского слоя, окружающего разделяющую плоскость и свободного от разделяемых точек, называют "векторами поддержки". Этот метод порождает новый класс алгоритмов, основанных на векторах поддержки, а НС, обучаемые с помощью этого метода, называют сетями с векторами поддержки 3).

АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ОСНОВНЫХ КОНЦЕПЦИЙ СТАТИСТИЧЕСКОЙ

ТЕОРИИ ОБУЧЕНИЯ НС

Анализ элементов статистической теории обучения [15] удобно проводить, используя более компактную (чем выше) форму обозначений. Пара векторов (x,y) — вход и выход НС — обозначается одной буквой z, тогда роль распределения P(x,y) займет вероятностная мера P(z). Таким образом, общая форма задачи обучения основана на понятии вероятностной меры P(z), определенной на пространстве Z, и наборе функций потерь {Q(z,а), ае Л}. Цель обучения достигается минимизацией функционала риска

R ( а ) = J Q ( z , u )d P ( z )                (6)

при условии, что вероятностная мера P(z) неизвестна, но имеется обучающая выборка в форме набора независимых одинаково распределенных (НОР) данных z 1, z 2, • • -, z n.                                (7)

Функция потерь Q ( z , а ) строится на основе функции отображения, реализуемого нейронной сетью (при текущем наборе значений а ее синаптических весов), поэтому два набора: набор функций потерь { Q ( z , а ), а е Л } и набор функций отображения НС { f z , а ), а е Л } — имеют взаимно однозначное соответствие (изоморфны), а численность их совпадает ⁴⁾. В связи с этим описываемые ниже характеристики этих наборов (энтропия, функция роста, размерность Вапника—Червонен-киса) относятся в равной мере одновременно к обоим наборам (множествам).

Чтобы минимизировать функционал риска (6) при неизвестной вероятностной мере P ( z ), используются возможности принципа МЭР. Ожидаемый функционал риска ⁵⁾ R ( а ) заменяется функционалом эмпирического риска (8), образованным на основе обучающего множества (7):

n

R эмпир. ( а ) = - X Q ( z i , а ).             (8)

«“

Принцип МЭР имеет общий характер и связан с методами решения ряда задач обучения (оценка регрессии с помощью метода наименьших квадратов (МНК), метод максимального правдоподобия для оценки плотности вероятности). Так, в задаче регрессии вводится (п+1)-мерная переменная, используется функция потерь (4) и функционал эмпирического риска (8) в виде Rэмпир (а) = = (1/n)X”=i (yi - f (xi,а))2, который следует минимизировать. Эта процедура соответствует МНК. Для выбора функции плотности вероятности из данного набора {р(х,а), аеЛ} при подстановке функции потерь (5) в (8) получается метод максимального правдоподобия, и, чтобы найти аппроксимацию плотности распределения, нужно минимизировать R эмпир.(а) = -(I / n) X ”= ln[ P (x i,a)].

К прикладным аспектам статистической теории обучения относится формализованная трактовка следующих этапов [1, 2, 6, 13-14].

• •    Обоснование использования принципа МЭР для оценки фактического функционала риска (ФР) R ( а ) и его минимального значения, которое может быть получено на НС с доступным ей набором отображений {f( z , а ), а е Л } (и соответственно с набором функций потерь { Q ( z , а ), а е Л }). Это значит, что требуется определить условия, при которых принцип МЭР может служить начальным звеном процедуры оценки фактического ФР ⁶⁾, т. е. показателя точности обобщения НС. Таким образом, рассмотренные ниже условия обеспечивают правомерность следующей цепочки соотношений⁷⁾:

  α _n

  
  

  = arg - min R

  а е Л :

  
  

  эмпир .

  
  

  1 А

  ( а ) = -£ Q ( z i , а

  n i = 1

  
  
  

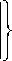
R (а n ) n . ---Вер. > R (а 0), где а 0 значение, которое а0 = arg {min R (а) } аеЛ

дает min R ( а ): а е Л

R эмпир. ( а n ) n -> R ( а 0 ).                (10)

Здесь и далее "Вер." — вероятность. Выражение (9) показывает, что решение, найденное с использованием МЭР, сходится к лучшему решению, которое может реализовать НС, а (10) показывает, что величина эмпирического риска сходится к наименьшему риску.

• •    Установление, насколько быстро наименьшее значение R _эмпир ( а ) сходится (при возрастании n ) к наименьшей величине фактического риска R .

• • Получение соотношений для границы раз-

• личия ЭФР Rэмпир и ФР R, которые зависят от размера обучающей выборки и меры многообразия отображений нейронной сети. Эта граница различия позволяет прогнозировать достижимый показатель обобщения НС.

Обоснование использования принципа МЭР

Обоснование использования принципа МЭР состоит в получении условия равномерной сходимости (т. е. сразу для всего набора { Q ( z , а ), а е Л }) эмпирического риска к действительному риску R ( а ) [12]:

lim Вер.^а^ ^{( а )} - ^R эмпир. ^{( а ) ]}> ^е г = ⁰

n /^         а е Л                            I           (11)

для любого малого е , где n относится к объему обучающей выборки, по которой формируется R _эмпир⁸⁾.

Значимость этого условия связана с содержащимся в нем утверждением, что любой анализ адекватности использования принципа МЭР должен предусматривать наименее благоприятный ("наихудший" относительно а е Л ) случай соотношения ^{R ( а )} и ^R эмпир. .

Логическая схема получения условия равномерной сходимости основана на концепциях, играющих важную роль в статистической теории обучения нейронных сетей. Это прежде всего относится к понятию энтропии для набора функций { Q ( z , а ), а е Л }) и одновременно для набора { f z , а ), а е Л } функций отображений, реализуемых нейронной сетью. Понятие энтропии вводится в два этапа: сначала для функций-индикаторов, а затем — для функций общего вида.

Энтропия набора (множества) функций-индикаторов . Энтропия набора функций-индикаторов { Q ( z , а ), а е Л }) (т. е. функций, принимающих только два значения 0 или 1) характеризует меру разнообразия этого набора (на выборке обучающих векторов z i , z ₂, ..., z _n ) величиной N \ z 1 , z ₂, ..., z _n ), представляющей число различных способов разделений (дихотомий) этой выборки, которые могут быть получены с использованием функций заданного набора. Величину Н ^Л ( z 1 , z 2 , ..., z n )= ln [ N ^Л ( z 1 , z 2 , ..., z n )], называют случайной энтропией, поскольку она образована с использованием (случайной) обучающей выборки, формируемой на основе распределения

P ( z 1 , z ₂,... , z n ). Математическое ожидание — вероятностное среднее (обозначаемое символом E) называют просто энтропией Н ^л (n ) набора функций-индикаторов { Q ( z , а ), а е Л } на обучающей выборке размера n :

H^Л ( n ) = E{ H^Л ( z i , z ₂,, z n )} =

= E{ln N^Л ( z i , z 2 , ^ , z n ). (12) Энтропия Н ^л ( n ) описывает ожидаемое разнообразие данного набора функций-индикаторов на обучающей выборке размера n .

Энтропия набора функций общего вида . Совокупность { Q ( z , а ), а е Л } функций общего вида, значения которых находятся в ограниченных пределах A <  Q (z, а ) <  B , ограничена n -мерным кубом со стороной B - A . Она может трактоваться как совокупность точек в этом кубе или как совокупность n- векторов q ( а ) = [ Q ( z 1 , а ), Q ( z ₂, а ),..., Q ( z n , а )]^т, каждый из которых определяется значением а е Л . Известно, что из такой совокупности можно выделить (минимальную по численности) Е -сеть векторов⁹⁾, число которых удобно обозначить N ^Л ( E ; z 1 , z ₂, ..., z _n ), т. к. это число зависит от Л , определяющего набор { Q ( z , а ), а е Л }, от величины е и от самой обучающей выборки z 1 , z ₂, ..., z n (поскольку последняя определяет совокупность векторов q ( a ): { q ( а ) = [ Q ( z 1 , а ), Q ( z 2 , а ),., Q ( z n , а )]^т, а е Л }.

Логарифм величины N ^Л ( Е ; z 1 , z ₂, ..., z _n ) (которая является случайной, как и обучающая выборка z 1 , z ₂, ..., z _n ) называют случайной Е -энтропией Вапни-ка—Червоненкиса:

Н ^л ( е ; z i , z 2 , ..., z n ) = ln( N ^Л ( Е ; z i , z 2 , ..., z n )).

Ее математическое ожидание Н ^л ( е , n ) = E{ Н ^л ( е ; z 1 , z ₂, ..., z _n ) чаще всего называется просто энтропией Вапника—Червоненкиса или VC-энтропией. Форма написания VC-энтропии Н ^л ( е , n ) соответствует тому, что она характеризует меру разнообразия набора { Q ( z , а ), а е Л } функций общего вида (а более точно — конечную Е -сеть этого набора) с точки зрения ожидаемого количества дихотомий выборки размера n из совокупности данных с распределением P ( z 1 , z 2 , ..., z n ).

• ⁹⁾    Набор векторов { q ( a ), а е Л } имеет минимальную Е -сеть q ( а ₁), q ( а ₂),., q ( а _n ), если существует N= = N ^ ( e ; z 1 , z 2 , ..., zn ) векторов q ( а 1 ),_t q C o, ),..., q ( а n ), таких что для любого вектора q ( a ), а е Л среди этих векторов может быть найден вектор q ( а r ), который Е -близок к q ( а * ). Это значит, что p ( q ( a * ), q ( a _r )) =

• • I x*x /       * X       X*X          /         XI —                    _

= min|Q(z,а )-Q(z,а,)|

Понятия энтропии имеют ту же направленность, но более конструктивную форму, что и условия равномерной сходимости типа (11), обеспечивающие правомерность использования принципа МЭР. Так, в задачах распознавания образов средствами НС применяются индикаторные функции потерь. В этом случае условие равномерной сходимости даже в более сильной (двусторонней) форме (13) обеспечивается при выполнении соотношения (14) [16]:

lim ВЫ max R(а) - R   .(а) > Е ^ = О n ^~         ае Л 1                      1

для любого малого е;

г H ^Л (n) п lim---— = 0.

n /^ n

Для задач более широкой постановки, в которых в качестве набора функций потерь требуется применение функций общего вида (не относящихся к функциям-индикаторам), условие двусторонней равномерной сходимости, обеспечивающее справедливость использования принципа МЭР для прогноза обобщения НС и оценки фактического риска, выполняется одновременно с соотношением (15) для энтропии Вапника—Червоненкиса:

H^Л (Е, n) _п lim-------- = 0

n/^ n

для любого малого Е.

Энтропия Вапника—Червоненкиса для набора функций общего вида строится, как показано выше, с использованием Е-сети ограниченной совокупности n-векторов {q(a)=[Q(z 1,а), Q(z₂,а),., Q(zn,а)]^т, аеЛ}.

Таким образом, обоснованность практического применения логической последовательности соотношений (9) и (10) определяется установленной в статистической теории обучения импликацией [11-13]:

lim H^(Е, n) = 0, Ve ^

n /^

[                            .

^ lim Вер J maX R (а) - R    (а)| > е ^ = 0, Ve.

n /^        ае Л 11

Границы различия рисков и прогноз обобщения нейронной сети

Условия для адекватности применения принципа МЭР, выраженные в форме предельных соотношений для энтропии, носят асимптотический характер и, строго говоря, могут использоваться только при очень больших размерах обучающих выборок. Поэтому представляет интерес оценка скорости сходимости минимума эмпирического риска к оптимально достижимому фактическому ФР, условие для получения этой оценки, установление такого условия в общей форме, которая пригодна для совокупности задач с различными видами вероятностной меры P(z1, z 2, …, z n), и получение границ различия эмпирического и фактического рисков, которые позволяют прогнозировать уровень обобщения нейронной сети после обучения.

Существующий подход к решению первой группы перечисленных вопросов (т. е. кроме границ различия рисков) удобно проследить на задаче распознавания образов, решаемой нейросетевыми средствами, где в качестве набора функций потерь {Q(z,a), aeЛ} используются индикаторные функции. Получение результатов здесь базируется на модификации и некотором развитии рассмотренной выше концепции энтропии, которая отражает меру многообразия набора функций потерь {Q(z,a), aeЛ} и ту же меру для набора {f(x,a), ae Л} функций отображения нейронной сети.

Помимо рассмотренной ранее энтропии набора индикаторных функций

H^л(n) = E{H^л(zi,z2,_,z_n)} =

= E{lnN^л (zi, z2,...,zn)

вводится модифицированная VC-энтропия (MVCE) H_M^Λ_VCE (n) и так называемая функция роста G^Λ(n):

^HM^ΛVCE(n) = ln{E[H^л (z 1, z2,_,zn)]},

G^л(n) = In | max N^л(z1,..., z_n)|.               (17)

I z 1,..., z„                                    I

Модифицированная VC-энтропия H_M^Λ_VCE (n) представляет логарифм ожидаемого (взвешенного по распределению вероятности) значения случайной энтропии N^л (z 1, z2, ..., z_n), а функция роста G ^Λ (n) является логарифмом случайной энтропии, максимизированной по возможным вариантам значений в обучающей выборке. Эти функции определены таким образом, что для любого значения n справедливо неравенство

H ^л (n) < HMvce(n) < G ^л (n).

На основе определения функций модифицированной VC-энтропии и функции роста могут быть даны основные положения элементов статистической теории обучения, относящиеся к группе поставленных выше вопросов.

Cкорость сходимости эмпирической оценки риска к его фактическому значению

В обязательном условии (необходимом и достаточном) для применимости принципа МЭР, которому должна удовлетворять любая НС, использующая этот принцип, нет информации о скорости сходимости минимального эмпирического риска к величине ФР НС при обобщении. Условием быстрой сходимости ФР при значении вектора a весов у НС, минимизирующего Rэмпир. , к оптимальному значению ФР в обобщении служит соотношение lim Hjmvce (n) = 0 . n ^^

При этом быстрая ¹⁰⁾ сходимость гарантирует экспоненциальное убывание вероятности превышения разностью рисков любого малого числа е:

Вер.{R(an) -R(а0) > е}

Надо заметить, что как соотношение, описывающее условие применимости принципа МЭР, так и условие быстрой сходимости справедливы только для данной вероятностной меры, т.е. для того распределения P(z1, z 2, …, z n), которое входит в формирование энтропий H^Λ (n) и H_M^Λ_VCE (n). Однако наиболее важно построить НС для решения многих различных задач — для различных вероятностных мер. Другими словами, желательно установить, при каких условиях принцип МЭР является адекватным и обеспечивается быстрой сходимостью независимо от вероятностной меры P(z), т.е. независимо от вида функции совместного распределения данных входа—выхода, используемых для обучения НС и для ее последующей работы на новых данных.

Таким условием для применимости принципа МЭР при любом виде распределения P(z) служит выполнение соотношения для функции роста

GΛ(n) lim n ^^   n

= 0.

Условие в этой форме обеспечивает также быструю сходимость.

Описанные основы понятий и концепций прикладной теории обучения НС позволяют рассмотреть метод получения границ для разницы ФР (при значении вектора а, минимизирующего Rэмпир ) и оптимального значения ФР в обобщении. Эти границы более строго определяют скорость сходимости и устанавливаются сначала для вполне определенной функции распределения, а затем это ограничение снимается и определяются "глобальные" оценки границы, ориентированные на любой вид распределения. Глобальные оценки границы как более общие несколько шире.

Ряд преобразований (описанных ниже) позволяет получить неасимптотические оценки, которые ориентированы на объемы обучающих выборок, реально имеющихся в прикладных задачах при решении их средствами нейронных сетей. Таким образом, оценки для скорости обучения и показателей достижимых уровней обобщения НС будут основываться на различного типа границах, которые оценивают пределы этих показателей для фиксированного количества элементов обучающей выборки, позволяют их прогнозировать и в известной степени держать под контролем.

Оценка скорости обучения НС

Получение неасимптотической (т.е. для заданного размера обучающей выборки) границы на скорость равномерной сходимости связано с введением нового понятия — размерности Вапни-ка—Червоненкиса (РВЧ) ^И). РВЧ служит для определения конструктивной границы на функцию роста G^Л (n). Показано [5], что функция роста может либо выражаться соотношением G ^Л (n) = n ln 2, либо быть ограничена величиной

G ^Л (n) < h | ln n +1 |, ( h J где h — это такое целое число, для которого G ^Л (n) = h ln2   и одновременно   G ^Л (h +1) ^

^ (h + 1) In 2 . Иначе говоря, функция роста может быть либо линейной функцией от n, либо быть ограниченной и иметь верхнюю границу в виде логарифмической функции.

Считается, что РВЧ набора функций-индикаторов {Q(z,а), аеЛ, Q(z,а) е (0, 1)} будет конечной, если функция роста для этого набора является линейной. Кроме того, считается, что РВЧ набора функций-индикаторов является конечной и равной h, если функция роста ограничена логарифмической функцией с коэффициентом h.

Конечность РВЧ набора функций-индикаторов (которые в качестве отображения могут быть реа- п) РВЧ не имеет ничего общего с обычным понятием размерности вектора, матрицы или пространства.

лизованы нейронной сетью) является необходимым и достаточным условием для адекватного использования принципа МЭР независимо от вероятностной меры. Конечность значения РВЧ обеспечивает также и быструю сходимость.

РВЧ имеет и несколько другую трактовку. РВЧ набора функций-индикаторов {Q (z ,а), аеЛ, Q(z,а) е (0, 1)} — это максимальное число h векторов z_ь ..., zh, которые могут быть разделены на две части всеми 2^h возможными способами путем использования функций этого набора. Если такое разделение возможно для любого числа n векторов, то РВЧ равно бесконечности.

Для набора функций общего вида, имеющих границы а и A: {a<Q(z,а) < A, аеЛ}, РВЧ определяется с помощью специальным способом образованного набора индикаторных функций. Вместо конечной функции общего вида создается функция-индикатор

I(z, а,в) = 9{Q(z, а) - в}, а е Л, (18) где в — некоторая постоянная; 6 — ступенчатая функция (функция Хэвисайда), принимающая значение 1, если ее аргумент (выражение в скобках) положителен, и принимающая значение 0, если аргумент менее нуля. Другими словами, функция 6 определяется выражением

9 (и) =

0 ,   если u< 0;

1,    если и > 0.

При этом в качестве РВЧ набора функций общего вида принимается РВЧ набора соответствующих функций-индикаторов (18).

Следствием этого правила определения РВЧ служат два положения, которые полезны в практическом приложении к нейронным сетям.

• •    Для набора линейных индикаторных функций (в n-мерном пространстве z 1 ,„z_n), которые имеют вид Q(z,а) = 9{5k=1 a_kz_k + а₀}, РВЧ равна h = n + 1, т. к., используя функции этого набора, можно разделить по крайней мере n + 1 векторов.

• •    Для набора линейных функций общего вида Q(z,а) = 5k=1 a_kz_k + а₀ (в n-мерном пространстве z 1 „.z_n) РВЧ также равна h = n + 1, поскольку этой величине (n + 1) равна РВЧ соответствующих индикаторных функций (если использовать а—в вместо «о, что не изменит набора индикаторных функций).

Можно, например, рассмотреть плоскость w*^Tx-b = 0, ||w*||=1, называемую A-разделяющей при условии, если она классифицирует векторы x следующим образом:

У =

1, если w *^Tx - b > A;

-1, если w *^Tx - b<-A.

Тогда для некоторой совокупности векторов x, принадлежащих шару радиуса R, набор А-разде-ляющих плоскостей имеет РВЧ h, величина которой ограничена в соответствии с неравенством h < min

|[А2

VL

n +1.

J

Это показывает, что, хотя в общем случае РВЧ набора плоскостей равна n+1 (где n — размерность входного пространства), величина РВЧ набора А-разделяющих плоскостей при большой величине А может быть меньше, чем n+1.

Как отмечено выше, величина РВЧ ограничивает функцию роста G^Λ (n) и, следовательно, дает форму условия адекватности использования принципа МЭР вне зависимости от распределения вероятностей. Тем не менее, справедливость этого условия пока гарантирована только для очень больших n, т. е. носит асимптотический характер. С точки зрения приложений НС желательно получение границ для различия минимального значения R_эмпир. от функции риска при обобщении R(а) для фактически реализуемых размеров обучающей выборки. Такие границы установлены в двух модификациях: свободные от типа распределения (толерантные) границы и границы, соответствующие определенному распределению, связанному со спецификой решаемой задачи. Имея в виду зависимость границ от n, их называют также границами для скорости сходимости процесса обучения НС.

Свободные от типа распределения (толерантные) границы для скорости сходимости процесса обучения получены Вапником [12], [13]. Для набора функций {Q(z,а), аеЛ}, имеющих конечное значение РВЧ и ограниченных как целое:

Для функций потерь НС в виде набора функций-индикаторов, используемых в задаче (бинарного) распознавания образов, постоянная B равна единице, так что в этом случае правая часть выражения (20) приобретает более простой вид.

Точные (зависящие от распределения) границы для сходимости процесса обучения определяют границы для степени отличия фактического риска от его эмпирической оценки .эмпир.(а) и учитывают информацию о вероятностной мере. При анализе задачи получения таких границ используется метод, основанный на так называемом теоретикомножественном подходе [2, 10].

• •    Допускается (по априорной информации), что вероятность P(z) относится к набору (множеству) P вероятностных мер, который является частью большего набора Pо, т. е. P(z)е P с P₀.

• •    Используется расширенное (обобщенное) определение функции роста

G^Л (8,n) = ln-! max Е_иnN^л(8;z₁,...,z„ ^. (22) [ P (z )е P⁽) J

Для функций-индикаторов {Q (z ,а), аеЛ, Q(z,а) е (0, 1)}и для экстремального случая, когда P = P0, расширенное определение G_P^Λ(ε, n) совпадает с простой функцией роста G^Λ(n) . Для другого крайнего случая, когда P содержит только P(z), обобщенная функция роста совпадает с модифицированной VC-энтропией H_M^Λ_VCE(n), выражение которой дано в (17).

В общем случае для ограниченного (константами A и B) набора функций потерь {Q(z,а), A< Q(z,а) < B, аеЛ} при больших n выполняется соотношение [10, 16]:

0 < Q(z, а) < B, а е Л , B — константа, (19)

выполняется условие в виде неравенства (20), которое связывает фактический риск R(а) и его эмпирическую оценку R_эмпир.(а). Неравенство (20) дает предел возможного превышения R(а) своей оценки R._эмпир (а). С вероятностью не менее 1-п одновременно для всех функций (19) выполняется ограничение (20):

Вер.- max f Q(z, а)dP(z) - - ]E Q(zi, а) > 8 - < а^еЛ J                 Hi=1

<12exp-

f gP (8/6(B - A);2n) n

- V

-

7       1 X A

+ ln(H)

B - A n ^J

n

.

Bε      4Rэмпир.(α)

R (а) < R эмпир.(а) +--11 +--,     (20)

2        Bε где h — значение РВЧ; е определяется выражением (21):

h(ln — +1) - ln п

8 = 4-----h---------- n

.

Показано, что из этого соотношения может быть получена другая форма различия фактического риска и его эмпирической оценки. Для достаточно большого n с вероятностью не менее 1-п одновременно для всех аеЛ (включая то а, которое минимизирует R_эмпир. ) справедлива граница различия фактического риска и его эмпирической оценки, определяемая выражением:

J Q( z, a)dP (z) <

• 1    n          IGp (s/6( B - A);2 n) - In n/12

• <-L ^Q(zi,^a)+ i----------------------------. (23)

П i=1         V             П               ⁽⁾

К сожалению, эта граница не конструктивна, поскольку нет метода для оценки обобщенной функции роста. Чтобы эти границы стали практически полезными и точными, нужна оценка обобщенной функции роста для данных набора функций потерь и набора P вероятностных мер, но метод получения оценки обобщенной функции роста пока окончательно не разработан.

Прогноз и контроль показателя обобщения НС, реализуемого сетью после обучения, может основываться на рассмотренных выше границах. Так, при больших значениях размера обучающей выборки n второе слагаемое в правой части выражения (20) становится близким к нулю. Тогда функционал эмпирического риска становится хорошей оценкой ФР при обобщении, который отражает показатель обобщения НС и либо косвенно, либо непосредственно (как в случае задачи распознавания образов) характеризует процент количества ошибок, среднеквадратичную ошибку аппроксимации и другие показатели обобщения НС.

Принцип структурной минимизации риска

Элементы прикладной теории, связанные с прогнозированием, контролем и "управлением" показателем обобщения обученной НС, включают условие адекватности применения принципа минимизации функционала эмпирического риска12), которое учитывает размер обучающей выборки и соответствует такому ее объему, каким практически располагает исследователь. Формализованное обоснование принципа МЭР, использующее ряд модификаций концепции энтропии набора функций {Q(z,а), аеЛ}, приводит к получению границ предельного различия ФЭР и ФР фазы обобщения нейронной сети с учетом размера обучающей выборки. Таким образом, эти результаты получены для малых объемов обучающих данных, обычно доступных при решении прикладных задач. Тем не менее, следует отметить некоторое несовершенство рассмотренного метода. Если при использовании соотношения (20) для границы скорости сходимости (предела различия минимума эмпирического риска и риска при обобщении) величина отношения n/h велика, то второе слагаемое в правой части (20) будет незначительно, и вследствие этого фактический риск R(а) очень близок к Rэмпир.(а), а малая величина Rэмпир.(а) обеспечивает малую величину фактического (ожидаемого) риска. Однако когда n/h мало, то даже малое значение Rэмпир.(а) не гарантирует малости реального риска. В этом случае минимизация R(а) требует нового принципа, который может быть получен минимизацией одновременно обоих слагаемых в (20). Одно из них зависит от величины Rэмпир., а второе зависит от РВЧ набора функций {Q(z,а), аеЛ}. При этом необходимо найти метод, который наряду с минимизацией Rэмпир. контролирует и "управляет" РВЧ обучаемой сети. Такой метод строится на основе принципа структурной минимизации риска (СМР) [5, 9].

Принцип СМР состоит в минимизации функционала риска относительно эмпирического риска и РВЧ набора фунций {Q(z,а), аеЛ} (являющегося отражением множества функций отображения, реализуемых НС). В наборе S функций {Q(z,а), аеЛ} вводится некоторая структура, состоящая из последовательности расширяющихся наборов (подмножеств) S_k функций {Q(z,а), ае Л_к}, таких что их объединение заполняет общий набор (множество) функций:

S 1 с S₂с... с S_n с... с S* = ^ Sk ,

(к)             (24)

S = S, где символ = означает, что объединение S* "плотно" в множестве S.

При этом к допустимым относятся структуры, обладающие тремя свойствами:

• •    S везде плотно в S, т.е. в S может быть найдена функция Q(z,а), достаточно близкая от функции, выбранной (любым образом) в S.

• •    РВЧ h любого подмножества Sk — конечная величина.

• •    Каждый элемент S_k структуры ограничен в целом (некоторой константой Bk):

0 < Q(z, a) < Bk при а е Л_к.

Принцип СМР предполагает, что для данной обучающей выборки {z 1, z₂,..., z_n}(численностью n) выбирается элемент структуры Sl, l = l(n) и выбирается такая функция из Sl , для которой гарантированный риск (20) является минимальным. Принцип предполагает существующее противоречие между качеством аппроксимации и сложностью аппроксимирующей функции (фактически сложностью структуры НС). При возрастании n минимум R_эмпир. снижается, однако слагаемое, ответственное за доверительный интервал (второе слагаемое в (20)), возрастает. Принцип СМР принимает во внимание оба фактора.

Метод СМР обеспечивает для любой функции распределения сходимость к лучшему решению с вероятностью единица [5, 9]. Этот метод является достаточно общим, независимым от распределения условием адекватности сходимости эмпирического риска к риску при обобщении. Функции Q(z,aП⁽n)), которые минимизируют риск R(anl⁽n)) на элементе Sl структуры, сходятся к функции, минимизирующей риск на всем множестве функций {Q(z,a), aeA}. При достаточно большой обучающей выборке (при n^ ”) асимптотическая скорость сходимости R(α^l_n⁽ⁿ⁾ ) к общему минимуму R(α) на всем множестве S определяется выражением ¹³⁾

выше представления об элементах СТО для задачи распознавания образов.

Метод разделяющих (гипер-) плоскостей¹⁴⁾ и его модификация [17–20]. Для минимизации эмпирического риска на наборе линейных индикаторных функций

f (x, w) = 9 -

n

X i=0

wix¹ r.

w e W

^{V (}n ) = rl ( n )

hl(n) ln(n)

+ Bl ( n yj---------- n

при условии, если изменение l = l(n) таково, что

Bl2(n)hl(n) ln(n) lim—--> n >^      n

В (25) Bl — это граница для функций из Sl, а rl(n) — скорость аппроксимации:

r_Un) = min [ Q(z, a) dP(z) - min [ Q(z, a) dP(z).

( ) ae Л₁ J                         ae Л J

Элементы теории построения алгоритмов обучения НС

Для выполнения процедур принципа СМР в обучающих алгоритмах нужно контролировать два фактора, присутствующие в соотношении (20) для границ:

• •    величину эмпирического риска;

• •    слагаемое, определяющее доверительный интервал в оценке (20), путем выбора из структуры элемента Sl с подходящей величиной РВЧ — и стремиться их оба минимизировать.

Метод удобно проанализировать на задаче распознавания образов, рассматривая обучение нейронных сетей двух типов:

• 1)    НС с прямым распространением сигнала (простого аналога взаимодействия нейронов) и

• 2)    НС "с векторами поддержки", появление которых связывают с определенным этапом развития статистической теории обучения (СТО).

Чтобы следовать этой схеме анализа, требуется введение ряда соотношений, уточняющих описанные

при обучающей выборке (x₁, y₁),...,(x_l, y_l) , где n-вектор xj = (x*,...,x”)T и yj e {0,1}, j = 1,...,l, требуется найти вектор параметров НС w = (w1, w2, …, w_n)^T, компоненты которого в качестве синаптических весов сети обеспечивают наименьшее значение для Rэмпир.(w):

₁l 2

Rэмпир.^(w)= у X [yj^-f^(xj,^w)]• ^{(28) l}j=1

К сожалению, в прикладных задачах набор линейных индикаторных функций часто оказывается неспособным обеспечить малое значение эмпирического риска [18]. В качестве возможности увеличения гибкости набора функций применяются два подхода.

• •    Использование более общего набора индикаторных функций, который является суперпозицией линейных индикаторных функций.

• •    Отображение входных векторов x в пространство более высокой размерности и создание в этом пространстве A-разделяющих плоскостей, у которых в слое толщиной A с каждой стороны плоскости не содержится разделяемых точек (векторов).

Первый подход связан с обучением НС обычной структуры, второй вариант связан с НС "с векторами поддержки". Как отмечено выше, сети такой структуры и алгоритмы для их обучения сформировались в одном из направлений СТО.

Сигмоидная аппроксимация индикаторных функций НС. Анализ требования минимизации функционала (20) в связи с обучением НС показывает, что непосредственное использование

¹³⁾ Об асимптотической скорости сходимости V(n) случайной величины En, n=1,2, ... к £₀ говорят, когда

V(n)^-1 | $_n - $₀ |     —Вер > c, где c — константа.

n >^

¹⁴⁾ Поскольку рассмотрение проводится в векторном пространстве распознаваемых "точек" x, то разделение их осуществляется гиперплоскостями. Этот несколько перегруженный термин сначала указан в форме "гиперплоскость", а далее для простоты будет говориться о плоскости, подразумевается, конечно, везде ее многомерность, т. е. по сути дела –— гиперплоскость.

В формуле (27) и следующих слагаемое с индексом 0 соответствует смещению нейрона. При этом считается, что условная дополнительная компонента x0=1, а w0 представляет величину смещения [7].

градиентного метода для набора строго индикаторных функций невозможно, поскольку для них градиент равен или 0 или 1. Поэтому индикаторные функции аппроксимируются сигмоидными функциями15)

n f (x, w) = 5 {J w.xi},           (29)

• i=0

где S — гладкая монотонная функция, для которой 5(-”) = 0 или —1, 5(+~) = +1.

Это — сигмоидные функции типа 5 1(и) =

• 1                    2arctg( и) + т

=-----------или 5 2 (и) =-----.

• 1    + exp(-и)2

При использовании одного из видов сигмоидной функции функционал

• 1^l

R эмпир/w) = jX (У* - f(x *, w))2

l i=1

становится гладким по w (непрерывно дифференцируемым), имеет градиент и поэтому может быть минимизирован с применением градиентных методов. Так, градиентный метод крутого спуска (по поверхности Rэмпир.(w)) использует правило обновления w в форме соотношения: w⁽n⁺¹⁾= w⁽n) - y⁽n) grad [rэмпир. (w⁽n))], где верхним индексом (n) указан номер итерации обновления; y⁽n) ^ 0 и обычно зависит от номера итерации. Для сходимости метода градиентного спуска достаточно, чтобы γ⁽ⁿ⁾ удовлетворяло условию: X Y⁽n) =~ и X [Y⁽n)]²<”, т.е. ряд из Vn) расходится, а ряд из [γ⁽ⁿ⁾]²— сходится.

Таким образом, идея состоит в сигмоидальной аппроксимации индикаторных функций на стадии оценки коэффициентов w (синаптических весов НС) и использовании индикаторных функций с этой аппроксимацией на стадии распознавания.

Обобщение этой идеи ведет к более общим структурам НС с распространением сигналов вперед (без обратных связей [21, 22]). Так, чтобы увеличить гибкость набора решающих правил при обучении, рассматривается суперпозиция нескольких линейных функций-индикаторов. Такая суперпозиция соответствует сети нейронов, вместо отдельного нейрона, для которого достаточно набора простых индикаторных функций. При этом все функции-индикаторы в этой суперпозиции заменяются сигмоидными функциями.

Метод вычисления градиента эмпирического риска для сигмоидной аппроксимации функции активации нейронов, связанный с алгоритмом обратного распространения [7], введен в работах [4, 5]. Показано, что РВЧ нейронных сетей зависит от вида сигмоидной фнкции и количества синаптических весов в НС. При некоторых общих условиях РВЧ сети ограничена (хотя значение РВЧ обычно очень велико). Если РВЧ не меняется в процессе обучения, то способность НС к обобщению (т.е. показатели точности выполнения требуемого от нее отображения на новой информации с прежними статистическими характеристиками) зависит от того, насколько хорошо НС минимизирует эмпирический риск на достаточно большом обучающем материале.

При минимизации эмпирического риска с использованием метода обратного распространения возникают три проблемы.

• 1.    Функционал эмпирического риска может иметь несколько локальных минимумов, и процедура минимизации гарантирует сходимость к некоторому из них. Поэтому в общем случае функция, найденная с использованием процедуры, основанной на градиенте, может быть далеко не лучшей. Качество полученной аппроксимации зависит от многих факторов и в особенности от начальной величины параметров алгоритма.

• 2.    Сходимость к локальному минимуму может быть довольно медленной из-за высокой размерности пространства синаптических весов НС.

• 3.    Сигмоидная функция имеет масштабирующий параметр, который влияет на качество. Чтобы выбрать этот параметр нужно сбалансировать противоречие между качеством аппроксимации и скоростью сходимости. Поэтому считается, что хорошая минимизация Rэмпир. во многих отношениях зависит от искусства исследователя.

Оптимальные разделяющие плоскости. Для получения структуры НС, альтернативной к НС прямого распространения, следует сначала рассмотреть "оптимальные" разделяющие плоскости (фактически гиперплоскости с плоскопараллельной зоной, свободной от точек обучающей выборки) [23].

В задаче бинарного распознавания обучающие данные {(x1,у 1), (x2,у2), _, (xl,yt); xeRn, yе {-1, +1}} могут быть разделены на два класса плоскостью wTx - b = 0, (31)

причем считается, что выход НС y = 1 соответствует x e класс 1, а выход у=-1 соответствует x е e класс2.

Набор векторов разделяется оптимальной плоскостью (или A-разделяющей гиперплоскостью), если безошибочное разделение этого набора на два класса достигается с помощью плоскости при пустом слое с максимальной толщиной А с каждой стороны этой плоскости [6].

Свойство разделяющей плоскости указывать, по какую сторону от нее лежит некоторый обучающий вектор xi, может быть представлено соотношением wT x i - b > 1,    если y, = 1;

w^Txi -b<-1, если yi = -1.

Более компактное описание этого свойства дает (эквивалентное по смыслу) выражение yi [wTx-b]> 1, i = 1,2,...,l.        (32)

Показано [6, 24], что при условии (32) плоскость будет оптимальной, если норма вектора w, определяющего нормаль (перпендикуляр) к этой плоскости будет минимальной. Поэтому для определения оптимальной плоскости требуется минимизация функционала (33) O(w) при дополнительном выполнении условия (32):

Ф(w) = 2||w II²=¹(w T w).        (33)

Решением этой задачи условной минимизации является "седловая" точка функционала Лагранжа (лагранжиана) L(w,b,а), а = (a1, .., al), который сводит задачу к безусловной минимизации за счет введения дополнительных параметров ai, называемых множителями Лагранжа:

L(w, b, а) = ~(w^Tw)- 2 ai {yi [w^Tx, - b] -1}, (34) 2              i=1

где ai — множители Лагранжа.

Поскольку здесь (для удобства) условия с множителями Лагранжа введены в функционал со знаком минус, то этот функционал должен минимизироваться относительно w, b и максимизируется относительно ai > 0. Решение w0, b0 и a^0 (i = 1,..., l) удовлетворяет условиям d L(w 0,b 0, ai(0)) n dL(w 0,b 0, ai(0)) n ----------------= 0,    ----------------= 0.

∂b                 ∂w

Явный вид этих условий (получаемый подстановкой развернутой формы лагранжиана (34)) позволяет выявить ряд свойств оптимальной гиперплоскости.

• •    Коэффициенты a'¹⁰ для оптимальной гиперплоскости удовлетворяют ограничению

2а(⁰⁾yi = 0, а > 0, i = 1,2,...,l.       (35)

i=1

• •    Параметр оптимальной гиперплоскости w₀ является линейной комбинацией векторов обу-

• чающего набора

wо = 2 ai⁽⁰⁾yixi, ai⁽⁰⁾> 0, i = 1,2,..., l.    (36)

i=1

• •    Решение удовлетворяет условию (называемому условием Куна—Таккера)

a(⁰⁾{[(x_zw 0) - b 0] y_-1} = 0.         (37)

Из этих условий следует, что только некоторые обучающие векторы в выражении (36) — "векторы поддержки" — могут иметь в разложении w₀ненулевые коэффициенты ai⁽⁰⁾. Векторы поддержки — это векторы xi, для которых в (32) достигается равенство, т. е. они поддерживают (принадлежат им) плоскости, лежащие с двух сторон от разделяющей плоскости и образующие слой (толщины 2А), свободный от обучающих точек. Поэтому получается соотношение:

w0 = 2 а""у,xi’   """ > ^{0      (38)}

Ξ где S — множество индексов совокупности векторов поддержки, определяющих w0.

Подстановка выражений для w0 обратно в лагранжиан (34) с учетом условия (37) дает функционал l1

W(а) = 2 ai-^2 aia j^i^jx T xj .

i=1

Остается максимизировать этот функционал в квадранте неотрицательных ai (ai>0, i = 1,2,.,l) при ограничении

l

2 aiyi= 0.                     (40)

i

Подстановка выражения (38) для w₀ в (31) приводит к плоскости в виде выражения, связывающего векторы поддержки:

l

2 а(⁰⁾x^Txi+ b = 0.            (41)

i=1

В случае, когда обучающие данные линейно неразделимы, может применяться метод получения квази-оптимальной разделяющей плоскости. Для этого используются новые переменные § (так называемые переменные бездействия, § > 0). Пе-ременые § служат допустимой величиной погружения некоторой части из обучающих точек в "свободный" слой 2А, принадлежащий оптимальной разделяющей плоскости для остальной (большей) части обучающих точек. Чтобы количество и величина нарушений оптимальности были наименьшими, в минимизируемый функционал вводится регуляризирующая компонента. Конструкция функционала имеет вид:

l

Ф( $) = w T w + C 2 $i, i=1

Использование описанного выше метода условной оптимизации на основе введения множителей Лагранжа (с переходом к безусловной минимизации по расширенному перечню параметров) приводит к тому, что оптимальная плоскость снова выражается соотношением (41) на векторах поддержки. Коэффициенты ai определяются путем максимизации того же квадратичного выражения (39), как и в случае линейной разделимости. Однако здесь требуется использовать несколько отличающиеся ограничения в виде условий (42):

l

0 < a_t< C; i = 1,2,...,l; 2ay = 0.       (42)

i

При отсутствии возможности разделимости анализируемого набора точек (векторов) плоскостью эта задача решается с помощью поверхности общего вида (в n-мерном пространстве). Для этого осуществляется преобразование в так называемое пространство признаков, которое имеет более высокую размерность (сравнительно с исходной размерностью векторов обучающей выборки) и в котором, как доказано Ковером (Cover T.) [27], может быть достигнута разделимость с помощью гиперплоскости. Такой метод при решении задачи распознавания образов используется нейронной сетью с векторами поддержки¹⁶⁾. Применяется концепция отображения входных обучающих векторов в пространство Z признаков, имеющее более высокую размерность, причем нелинейное преобразование выбирается априорно и "произвольно". В этом новом признаковом пространстве строится оптимальная разделяющая плоскость. Целью является создание ситуации (подобно рассмотренному ранее примеру), при которой для A-разделяющих гиперплоскостей РВЧ определяется отношением R2/A². Для получения хорошего обобщения у НС следует контролировать РВЧ и уменьшать ее величину путем построения A-разделяющей гиперплоскости с максимальным значением A-слоя. Собственно, ради повышения A и используется пространство высокой размерности.

Бозером и Гуйоном (Boser B., Guyon I.) [19] было отмечено, что для описания оптимальных разделяющих плоскостей в признаковом пространстве и для оценки компонент вектора нормали (39) (представляющей эту разделяющую плоскость) требуется использовать произведение двух векторов z(x1) и z(x2), которые являются изображениями в признаковом пространстве входных векторов x₁ и x₂. Поэтому, если есть возможность оценить произведение двух векторов в признаковом пространстве z(x1) и z(x2) в виде функции двух переменных во входном пространстве zi^Tz = K(x,xi), тогда будет возможно и создать решения, которые эквивалентны оптимальной плоскости в признаковом пространстве. Чтобы получить это решение, следует заменить произведение xi^Txj в (39) и (41) функцией K(xi, xj). Другими словами, создаются нелинейные решающие функции, которые во входном пространстве имеют вид:

2 ^aiK^(xi,^x)+b ( векторы поддержки x_i )

I (х) = sign

I

которые эквивалентны линейным решающим функциям (33) в признаковом пространстве. Коэффициенты ai в (43) определяются путем решения уравнения (44) при ограничениях (42):

l₁l

W^(а) = 2 ^ai—^2 ^ai ^аjy УК⁽xi , xj^{). (44)} i=1 ²i, j=1

i * j

В то же время, согласно функциональному анализу, общая форма произведения векторов определяется посредством симметричной, положительно определенной функции K(x,y), удовлетворяющей условию Мерсера [28]: для любого сигнала с конечной энергией (J z(t)² dt > 0) справедливо неравенство J K(x, y)z(x)z(y)dxdy > 0. Поэтому любая функция K(x,y), удовлетворяющая условию Мерсера, может быть использована для получения правила (43), что эквивалентно созданию оптимальной разделяющей плоскости в некотором признаковом пространстве.

Обучаемую НС, реализующую отображения в виде (43), называют нейронной сетью с векторами поддержки [29]. Использование различных выражений для внутреннего произведения в форме K(x,xi) позволяет создавать различные НС этого типа с произвольным типом решающих поверхностей (нелинейных во входных пространствах) [30–32].

Например, сеть с радиальными базисными функциями (РБФ-сеть) [6, 33] и решающими функциями типа

( i

f(x) = sign 2

i=1

V

II x - xi II2

2 σ

yi^ai exP-

(где ai, i = 1,..., l и a — параметры РБФ-сети) может быть выполнена с использованием функций вида

K (x, xi) = exp-

II x - xi II²

2 σ

В этом случае

НС при обучении будет находить как центры xi, так и соответствующие веса ai. Такая НС обладает некоторыми полезными свойствами:

• •    задача оптимизации этой НС имеет единст-

• венное решение;

• •    процесс обучения идет довольно быстро;

• •    использование введенного вида решающего правила позволяет в процессе обучения сети определить набор векторов поддержки;

• •    получение нового набора решающих функций достигается простым изменением только функций (ядра K(x,xi)), которые определяют скалярное произведение в признаковом пространстве Z.

Способность к обобщению у нейронной сети прямого распространения (НС_ПР) и сети с векторами поддержки. Способность к обобщению у НС_ПР и НС с векторами поддержки (SVM) основана на рассмотренных элементах статистической теории обучения и на полученных оценках для скорости сходимости эмпирического риска к его действительной величине. Кроме того, чтобы гарантировать высокие показатели обобщения обучаемой сети, нужно построить структуру S1 с S2 с... с Sn с... с S на наборе решающих функций S ={ Q(z,а), аеЛ} и затем выбрать как подходящий элемент Sl в структуре, так и функцию Q(z,an) е Sl в этом элементе, которая минимизирует границу (20). Граница (16) может быть переписана в простой форме:

R^(аn ) — R эмпир.

(a n) + П

( „

V hl(n)

где первый член — это оценка риска, а второй является доверительным интервалом для этой оценки.

При создании НС определяется набор допустимых функций с некоторым значением РВЧ h*. Для данного размера n обучающей выборки величина h* определяет доверительный интервал Q(n/h*). Поэтому формирование НС связано с выбором структуры, подходящей для данного обучающего набора. В период обучения НС минимизируется первый член в границе (45) (количество ошибок на обучающем наборе).

Если при построении НС она будет выбрана слишком сложной (относительно доступного набора обучающих данных), то доверительный ин- тервал Q(n/h*) будет большим. В случае если даже возможно минимизировать эмпирический риск до нуля, то количество ошибок на тестирующем наборе (т. е. при обобщении) может оказаться все же большим. Этот случай называют переподгонкой или избыточной подгонкой (под тонкую статистически случайную структуру обучающей выборки). Чтобы избежать избыточной подгонки (и получить малый доверительный интервал), следует стремиться создать НС с малой величиной РВЧ. Поэтому для получения хорошего обобщения у НС нужно, во-первых, предложить подходящую архитектуру НС и, во-вторых, настройкой параметров НС получить функцию отображения, которая минимизирует число ошибок на обучающих данных. Совместное решение этих задач для НС осуществляется на эвристической основе, или, по-просту говоря, с помощью интуиции и искусства исследователя.

В методах сетей с векторами поддержки можно управлять обоими параметрами: в случае задачи распознавания с разделимостью обучающих точек получается единственное решение, которое минимизирует эмпирический риск (возможно, вплоть до нуля) путем использования A-разделяющих гиперплоскостей с максимальным A-слоем (т.е. на основе получения набора отображений НС с наименьшей величиной РВЧ).

В общем случае для той же задачи получается единственное решение, когда выбирается сбалансированная величина параметра C в минимизируемом функционале Ф(^) с регуляризирующей компонентой, т. к. от C зависит предпочтительное соотношение между оценкой ошибки обобщения и ее доверительным интервалом.

ЗАКЛЮЧЕНИЕ

В рамках прикладной статистической теории обучения показан единообразный способ формализации группы задач, решаемых средствами нейронных сетей (НС) супервизорным методом ("с учителем"): распознавание образов, нелинейная регрессия и оценка плотности распределения вероятности. При этом применено вероятностное описание по входу и выходу НС с требованием ориентироваться не на сами вероятностные меры, а только на известные данные обучающей выборки. Три указанные задачи рассмотрены в терминах понятий: набор функций отображения НС, функция потерь и функционал риска. Все они параметризованы вектором а, компоненты которого представляют совокупность настраиваемых синаптических весов НС.

Следуя работам [1-5], используется нетрадиционное компактное представление обучающей выборки в форме z1, z2, …, zn (где zi объединяет вход сети xi и ее выход yi ), многообразия наборов (множеств) функций отображения НС {f(z,α), α∈Λ}, функций потерь {Q(z,α), α∈Λ}, фукциона-лов эмпирического риска {Rэмпир.(α)}(среднего от функции потерь) и соответствующих функционалов риска {R(α)}(функций потерь, взвешенных по вероятностной мере P(z)). В этом представлении даны отмеченные выше три основные задачи, решаемые с помощью НС.

Рассмотрены основные концепции элементов статистической теории обучения.

• •    Принцип минимизации эмпирического риска (принцип МЭР).

• •    Условия правомерности его применения в форме наличия сходимости к нулю вероятности максимального (по набору отображений) отличия величины R(α) и Rэмпир.(α). Фактический риск непосредственно или косвенно характеризует ожидаемую частоту ошибок НС при тестировании (ошибок на стадии обобщения).

• •    Базовые для статистической теории обучения понятия энтропии, VC-энтропии, модифицированной VC-энтропии и функции роста — для обучающей выборки или усредненно по вероятностному распределению обучающих данных, которые разным образом характеризуют меру многообразия набора функций потерь {Q(z,α), α∈Λ} (или изоморфного ему набора функций отображения НС).

• •    Условие правомерности расширенного применения принципа МЭР, который использует понятие энтропии и условие быстрой сходимости к нулю отличия R(α) и Rэмпир.(α), выраженные через модифицированную VC-энтропию и функцию роста.

• •    Для скорости сходимости процесса обучения приведены границы, основанные на размерности Вапника—Червоненкиса и функции роста. Границы на скорость сходимости приспособлены к реальному (небольшому) количеству обучающих данных и получены в двух формах: толерантные границы, справедливые независимо от вида распределения вероятностей, и точные (зависящие от распределения) границы. Эти границы позволяют прогнозировать и в определенной мере влиять на показатели обобщения НС в процессе ее функционирования после завершения обучения.

• •    Рассмотрен принцип структурной минимизации риска, который предусматривает получение возможно лучших показателей обобщения НС путем одновременной минимизации Rэмпир. и размерности Вапника—Червоненкиса набора функций потерь {Q(z,α), α∈Λ}(или изоморфного ему набора функций отображения НС).

• •    Изложены элементы теории построения алгоритмов обучения НС. Для задачи распознавания образов рассмотрен метод построения оптималь-

• ной разделяющей (гипер-) плоскости, использующий понятие "векторов поддержки". Метод приспособлен для линейно разделимой совокупности точек (образов) и имеет приближенную форму для случая не полностью разделимой совокупности образов.

• •    Показано, что для неразделимой совокупности образов целесообразно преобразование входного пространства в пространство признаков более высокой размерности, в котором уже может быть реализована линейная (с помощью гиперплоскости) разделимость образов. Для этого достаточно произведение векторов заменить некоторой симметричной функцией ("ядром") K(x,y), удовлетворяющей условию Мерсера.

• •    Подход на основе построения ∆-разде-ляющей ("оптимальной") гиперплоскости и перехода в признаковое пространство более высокой размерности применяется в НС с векторами поддержки (support vector neural networks), сетях с радиальными базисными функциями (RBF-сетях) и может быть использован в сетях прямого распространения сигнала общего вида (без обратных связей).

Таким образом, рассмотренные элементы статистической теории обучения показывают, что "абстрактный" анализ помогает раскрытию общей модели обобщения, реализуемого нейронной сетью. Согласно этой модели, способность к обобщению обучаемой НС зависит от меры многообразия отображений у НС. Это понятие более емко, чем просто размерность пространства или число свободных параметров у функции потерь). Оно является основой в оценке границы различия эмпирического риска и ошибки обобщения НС в фазе ее функционирования.

Развитие SVM-методов продолжается в направлении уточнения границ различия, использующих оценки функции роста и РВЧ, расширения области применения структур НС с векторами поддержки (SV-структур НС) и создания ядер K(x,y) с желательными свойствами инвариантности.