Элементы структурной механики деформируемого твердого тела

Непосредственный континуальный подход в механике сплошной среды ограничен наличием микроструктуры (субструктуры) каждого реального материала, которая проявляется в качественном изменении физических свойств на некотором уровне. Поэтому при феноменологическом описании материала часто вводятся многоуровневые континуумы.

С другой стороны, необходимость описания дефектов структуры (дислокации, вакансии, внедрения и т. п.) привела к так называемой континуальной теории дислокации, основы которой изложены в блестящей работе Кренера [I]. В этой теории внутренние напряжения, возникающие в телах при неоднородном и необратимом деформировании, могут быть описаны в рамках классической теории упругости путем расширения геометрического аппарата, традиционно используемого в механике деформируемого твердого тела (МДТТ).

Наконец, макроскопическая среда первого уровня является, вообще говоря, неоднородной и при ее использовании важную роль могут играть методы осреднения МДТТ [3]. Ниже мы коснемся элементов описания континуума с учетом микроструктуры, причем для простоты рассмотрим случай малых деформаций, евклидовой геометрии.

L Двухуровневое описание континуума

Пусть каждая точка (х^х^х^) е К макроконтинуума (первого уровня) сама представляет собой микроконтинуум (второй уровень) с объемом Р’^(х\ точки которого описываются координатами (б,^»^)⁶ И^1х>. Тогда каждой точке (£/,&’&) микроконтинуума, принадлежащего точке (x_/,x₂,x_J), припишем плотность р^^х,^ . Радиус-вектор этой точки обозначим через г^^х,^). Цен тр масс микрообъема можно описать радиусом-вектором г(х)

р(х)г(х) = J p^x,^r^4x\x,f)d^ ,                        ( I . I )

где р^х) - макроплотность вещества:

Введем радиус-вектор г'(х,^) по формуле г\х,£) = ^(x,^)- г(х).

Тогда для векторов скорости

, w \ dr

^ЧХ’^~5Г’ ^)^, VW=^(1.4)

имеем в соответствии с (1.1) - (1.3):

pW^=-^ $ pVV’^V’^YО-

F(x)

V^ = V + ?'(1-6)

Введем также в каждой точке микроконтинуума скорость диффузионного потока /^^х,^),

Y^Y^) = р(т)(х,5)[р(г)(х,5)- v(x)] = p^v'(1.7)

и массовую концентрацию вещества с^^х.^)

сиЧхх,^ = р(хЧх,£)/р(л).(1.8)

Из (1.5) - (1.8) видно, что

7^7 \j(X,

’ у<Х)                        У у(х)

Сформулируем теперь три основных постулата механики сплошной среды: о сохранении масс

dV = 0;

(1 10)

об изменении количества движения

pW^dV^

dP = j J p^(x)F^dK; kLH¹¹

dV +

(1.11)

и oo изменении момента количества движения

I r^vx p^v 'al^ V

х p^(x}F^{x}dV. dV +

(1.12)

+ J Jr+A'^iZr, di.

Здесь введены плотность массовых сил F^x\x,^ и плотность поверхностных сил 5и'(х,^), распределенных по поверхности 2^х\ ограничивающей микрообъем К'х\ в каждой точке х поверхности 1, ограничивающей макрообъем К.

Следствием постулата (1.10) является уравнение неразрывности, которое при эйлеровом описании движения имеет вид:

др ( '

~-¥div\pv Y-0.                                             (1.13)

Если же в каждом микрообъеме протекает Л' химических реакций со скоростью Jд^Р = 1,2,—,N^, то имеем

"~"^ +             XvAx>^JAx’^ ■          (! ,4)

(Л           L                 р=1

где v_p - некоторые стехиометрические коэффициенты [3]. При осреднении левой и правой частей (1.14) по микрообъему получим уравнение неразрывности (1.13), ибо

ТТЛ I S’'nV^fK^aV'e, ^{= 0}-                         С•¹⁵>

Для получения следствий из постулата (1.11) воспользуемся определением (1.5), а также

^pVWaV^pFlxY                        (1.16)

V

W^"^^'             (1Г)

Тогда получим уравнения движения сплошной среды dv -

at dx- где учтено, что

^ = 8^, S^a^e^                            (1.19)

причем и = л,ё, - единичный вектор нормали в точке (х_;,х₂,х/) поверхности Е . а ё, - ортонормированный репер [4], а = сг^ё^ - тензор напряжений.

Выразим теперь в (1.12) радиус-вектор г1^ через сумму г и г' согласно (1.3) и введем обозначения:

V'-p^F^aV^J^M^Y                   (1.20)

f^F'pV^n^AxlM^Y                  (1.21)

~L [r'S^a^iXx),                           (1.22)

I/(x) J                ъ          7                                                                 • где величина /(х) характеризует момент инерции микрообъема и вообще говоря является тензором, т.е. вместо Дх)ю(х) следовало бы писать

J <6 = J_ijto_je_i.                                                                 (1-23)

Однако, следуя общепринятым обозначениям (5). мы примем форму записи (1.20). Здесь ю - так называемый спин-вектор [5] dm

^ = ~7<                                                     (1.24)

dt

М(х) - массовый распределенный момент, а 2<л>- поверхностный распределенный момент, который может быть записан по аналогии с (1.19) в виде

^^йпн Q=W-                       (1.25)

где ц = р^ё®^ - тензор моментных напряжений. Из постулата (1.12) с учетом уравнений движения (1.18) получим: dco -       -

(1.26)

J—= JM+i. xS, +—-. dt                  dx_;

• 2.    Кинетика двухуровневого континуума

Можно ввест и сразу кинематическое описание, соответствующее принятому допущению о малости деформаций. Однако иногда при таком описании вектор перемещения теряет свой физический смысл [6].

Поэтому рассмотрим два состояния: отсчетную конфигурацию с радиусом вектором ^*’(х,^) и актуальную - с радиусом-вектором г^^х,^ . Будем считать (х'.х2^2) - лагранжевыми координатами макрообъема, а (У,У,У^ - лагранжевыми координатами микрообьема.

Тогда вектор перемещения можсг быть определен следующим образом: й^х,^ = F^{(x^) - ^(^Ч) ■                                  (2.1)}

Расстояние между двумя бесконечно близкими точками отсчетной конфигурации определяется с помощью величины ,т1*)

dS2 = dr^5 ■ сК?5 =     - -^— dx'dxi +

°      °      ° ax* ax1

(2.2)

—- • — -.-d^dy + 2 -—- ■    dx‘dy,

ay ау         ах- ау а расстояние между этими же частицами в актуальной конфигурации - с помощью величины dS2 = dr^1’ -dr^'^ -------. dxsdxj + ах Эх1

9^

аУу еу

d^dy+2-™

а?^^ . , -----~dx‘dy. ay 5

(2.3)

Меры деформации естественно определить полуразностью выражений (2.3) и (2.2)

dS2 -dS2 • ■     ,     - .            . .

---—— = e^dx'dx¹ + e^dydy + &_ijdx‘dy.                   (2.4)

Из сравнения (2.2) - (2.4) имеем, учитывая (2.1):

1(	ей	ай ай	_ Si
е=; = ~	——--.	. — +—-.		(2.5)
4 2\	,ах‘	Эх1 дх	2 ах1 ’)
■ Ч	ай	ай ай	ай
£н = Т	---— .		• ё, +—т-5, ,	(2.6)
о 2(	.9У	sy ау	1 ay ’)
71	(ай	ай ай	ей )         .
0Н = Ч	—	•     г + г	■ё, +--г-ё, .	(2.7)
	1 ах1	ау ах1	1 ау ')

Тогда в случае малых деформаций имеем:

1( Ai₍ At; , IГ 9ц. Ai Л

C‘j = 2+ ^J’ £ij = 2    + ^j’

(2.8)

Ait Aij d^j +Sti '

Поэтому за кинематические характеристики можно принять величины ^, е_Х) и спин-вектор <5 с компонентами

^k ”^ijk

Ai_x Ai, д^ ⁺ дх,

(2.9)

В качестве другого возможного набора кинематических характеристик можно принять тензоры дисторсии р и Р':

Однако в силу того, что элементарная работа внутренних сил из соображений размерности может быть записана в виде

8Л = а_и8р₎+^38В_и.                                    (2-11)

где as,y - так называемый тензор изгиба-кручения [7]

®и=^юи’                                            (2.12)

наибольшее распространение получил так называемый континуум Коссера [5], для которого принимается, что микроконтинуум не может деформироваться: б;_} = 0.

Для такого континуума система шести уравнений (1.18) и (1.26) замыкается определяющими соотношениями типа

"-j=^Fij^^,  Aj^G^P,^,                      (2.13)

где Р_Х) и G₍j- некоторые операторы представленных аргументов. В частности для упругой среды (2.13) имеет вид:

°ij -G,]klPki + Aijki®ki,

(2.14)

Mij = ^ijklPkt + flijkl^kl’

• 3.    Основные соотношения континуальной теории дислокаций

Если тело, в котором отсутствуют какие-либо напряжения (состояние А), подвергнуть внешнему воздействию (напряжению, нагреву, радиоактивному облучению и т. п.), а затем убрать эти воздействия, тело может не вернуться в исходное состояние. В нем могут остаться собственные напряжения (состояние Б), освободиться от которых, оставаясь в трехмерном пространстве, нельзя.

Однако мы можем мысленно разрезать тело на бесконечно малые объемные элементы (микрообьемы) и каждый такой элемент разгрузить. В результате тело нарушит свою связность (состояние В) [1].

Все три состояния (А, Б, В) отнесем к одной системе координат (х;,х2,х5). Разность координат одной и той же материальной частицы состояний Б и А назовем полным вектором перемещений и . Разность координат состояний В и Б - вектором упругих перемещений м и, наконец, состояний В и А - вектором пластических перемещений йр .

Разность двух векторов перемещений в двух бесконечно близких точках каждого состояния обозначим соответственно через Зй°,8i,8i^p.

Введем тензоры дисторсии Р° ,Р, Р^Р по формулам

8и” = P^dxp 6и^ = PijdXp 8u^p = Padx,.                       (3.1)

Очевидно, что &i° представляет собой полный дифференциал

Каждый тензор дисторсии может быть разбит на симметричную и антисимметричную части Например.

Рц ^s.j+^jkWk-                                          (³-3)

где

=i(^+A0-                             (ЗЛ)

Очевидно, что пластические деформации £р не удовлетворяют условиям совместности. Тензор несовместности определяется соотношением [1]

• т] = -Ink е = -V х ерх V - V х ex V(3.5)

или в компонентах:

tlij = ~^ikl^ jmnekn,im =^'i к ! ^ ; m пек nJ m ■(3-6)

Тензор плотности дислокаций а легко определить, зная пластическую деформацию:

a- PPxV = -pxV.(3.7)

откуда вытекает a-V = O.(3.8)

В компонентной записи соотношения (3.7) и (3.8) имеют соответственно вид:

«1т=-етмРи,к ^mkjPij.k-< а1т,т=0.                                                   (3.10)

Тензор изгиба-кручения (2.12) в безиндексной форме вводится следующим образом:

аг = d>QV .                                                        (3.11)

В случае односвязного тела с дефектами при обходе по замкнутому контуру Z

Q=^«df\                                      (3.12)

7 '

b = f (е- г ’ х аг )df',                                                (3.13)

мы получаем гак называемый общий вектор поворота дислокаций £2 и общий вектор Бюргерса b [7].

Считая тензор изгиба-кручения <е независимым от спин-вектора у . т.е. невыполнимыми соотношения (2Л2) и (З.Н), можно ввести тензор плотности дислокаций 9:

6=-а:хМ.                                             (3.14)

Очевидно

0-Х/-О.                                                    (3.15)

Вводя плотность внедрения дисклинаций / по формуле trce = y (се„=у),                                         (3.16)

получим связь между заданными распределениями дефектов а, 6, у \ а = - exV - у I + №Т.                                      (3.17)

где I - единичный тензор. В компонентах выражение (3.17) имеет вид

«im ^mkj ^еУ,к ~ Y^im + <®mi                                        (3-18)

Таким образом, при наличии дефектов и при заданных плотностях их распределения а, 0, у , задача определения статических внутренних напряжений заключается в решении девяти уравнений

7 eV х fxV = -V х a-N х (у I)+ 0                        (3.19)

и девяти уравнений

V х ах V -- -V х 0                                              (3.20)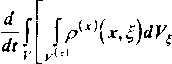

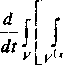
относительно девяти компонент тензора напряжений о и девяти компонент тензора моментных напряжений ц . При этом заданы определяющие соотношения Еч - QyUaU + ^ijkl^klf ®у ~ ^ijkl^kl *^чуЦк1, (3.21) и. кроме того, на границе тела £ заданы граничные условия ^«7Z =S*i ^"v ^ = ef (3.22) и условия равновесия среды ( 9 ° У        1 \Sxi    j) = 0. 2 (3.23) (a0ij + JM: kl        J = 0. (3.24) Если среда рассматривается неоднородной, то применяя метод осреднения. описанным. например, в [3] можно исходную задачу свести к рекуррентной последовательности решения двух специальных задач: для однородной среды с эффективными характеристиками и неоднородной на "ячейке периодичности" для определения этих эффективных характеристик.

Библно|рафический список

• 1.    Kroner Е. Kontinuums theorie der Versetrungen und Eigenspannungen. Erg. and Math. 1958. 5 1 - 179.

• 2.    Де Гроот С.. Мазур II. Неравновесная термодинамика,- М.: Мир. 1964,- 456с.

• 3.    Победря Б.Е. Механика композиционных материалов.- М.: Изд-во Моск, ун-та, 1984,- 336с.

• 4.    Победря Б.Е. Лекции по тензорному анализу,- М.: Изд-во Моск, ун-та, 1986,-264с.

• 5.    Nowacki W. Teoria niesymetrycznej.- Warszawa, PWN, 1981.- 380s.

• 6.    Победря Б.Е. О взаимосвязи геометрической и физической нелинейности в теории упругости и о смысле перемещений// Изв. АН Арм.ССР. Механика.-1987,-T.XL. №4.-С. 15-26.

• 7.    Де Вит Р. континуальная теория дислокаций.-- М.: Мир, 1977,- 208с.