Элементы теории отрицательно-нулевой обратной связи в адаптивных фрикционных муфтах

Введение. В адаптивных фрикционных муфтах (АФМ) второго поколения [1] применяется управляющее устройство (УУ) отрицательно-нулевой обратной связи. Достоинством таких муфт является повышенная нагрузочная способность за счёт введения в конструкцию фрикционной группы, не охваченной отрицательной обратной связью [1, 2]. Однако при практическом применении точность срабатывания АФМ не всегда отвечает требованиям по защите приводов технологического оборудования от поломок в результате случайных перегрузок [3].

Отличительные особенности адаптивных фрикционных муфт второго поколения с отрицательно-нулевой обратной связью [1]:

• —    наличие в составе дополнительной фрикционной группы, которая не охвачена отрицательной обратной связью (так называемой «нулевой» обратной связью), как основная фрикционная группа; — более высокие (при равных конструктивных параметрах) нагрузочная способность и точность срабатывания (скорость и качество срабатывания муфты) [2, 3].

Постановка задачи исследования. Установление закономерности изменения величины коэффициента усиления (КУ) обратной связи в зависимости от величины коэффициента трения в АФМ второго поколения.

Решение задачи. Объект исследования — АФМ второго поколения (базовый вариант) — представлен схемой (рис. 1).

Соосные одна другой полумуфты 1 и 2 кинематически связаны между собой двумя фрикционными группами (ФГ):

• —    основной (ОФГ), состоящей из дисков трения 3 и 4;

• —    дополнительной (ДФГ), включающей диски трения 5 и 6.

Диски 3 и 5 связаны в окружном направлении со ступицей нажимного диска 7, диски 4 и 6 — с барабаном полумуфты 2.

Нажимной диск 7 смонтирован на ступице полумуфты 1 и лишён кинематической связи с ней в окружном направлении, за исключением незначительного трения, не учитываемого в дальнейшем исследовании.

Работа выполнена в рамках инициативной НИР.

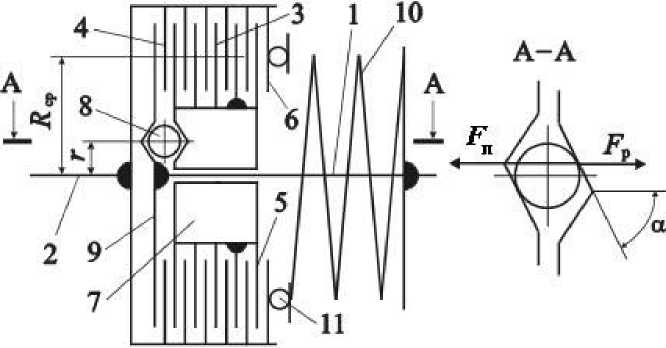
Рис. 1. Принципиальная схема АФМ второго поколения (базовый вариант)

УУ АФМ выполнено в виде тел качения 8, которые размещены в скошенных гнёздах нажимного диска 7 и упорного диска 9, жёстко закреплённого на ступице полумуфты 1 (см. рис. 1, сечение А—А).

Силовое замыкание пар трения ОФГ и ДФГ осуществляется пружиной 10, передающей усилие через упорный подшипник 11.

Вращающий момент АФМ складывается из суммы двух моментов сил трения: ОФГ и ДФГ.

В соответствии с этим можно записать:

Тп = Т + Т2,(1)

где Т ₁ — момент сил трения пар ОФГ; Т ₂ — момент сил трения пар ДФГ.

Моменты сил трения Т ₁ и Т ₂ соответственно равны:

Т1 = zRcpf (Fn - Fp),(2)

Т2 = ZiRcpfFn ,(3)

где z — число пар трения ОФГ; Rср — средний радиус поверхностей трения фрикционных дис- ков ОФГ и ДФГ; f — коэффициент трения; Fп — сила натяжения пружины 10; Fр — распор- ная (отжимная) сила УУ (см. рис. 1, сечение А—А); z1 — число пар трения ДФГ.

Величину распорной силы УУ можно определить по формуле:

F p = Т у Т tga,                               (4)

где α — угол скоса боковой стенки гнезда под тело качения 8 (см. рис. 1, сечение А—А); r — радиус окружности, на которой расположены тела качения (см. рис. 1); Т ₃ — момент силы трения фрикционных дисков 3 и 4, связанных со ступицей нажимного диска 7.

Момент силы трения Т ₃ вычисляется по формуле:

Т 3 = ( z - 1 ) R cp f ( F n - F p ) .                                       (5)

В соотношении (5) учтено то обстоятельство, что компоновка ОФГ построена по типу «ведущая пара трения — ведомые пары трения».

После подстановки правых частей соотношений (3) и (5) в выражение (4) получим:

z + ( z -1) F =F Cf ——⁽--- )

^p п 1 + ( z - 1 ) Cf

Здесь C — КУ АФМ, вычисляемый по формуле:

R

C = — tga. r

В соответствии с соотношением (6) и на основе выражения (2) найдём:

Т 1 = zF n R cp f

1 - z 1 Cf

1 + ( z - 1 ) Cf

Используя соотношения (2) и (8) в равенстве (1), найдём выражение для вычисления величины полного вращающего момента АФМ:

T = F R f z ⁺ z i zi^Cf *^{n FR cp}' 1 + ( z - 1 ) Cf ■

При настройке АФМ с учётом минимального значения коэффициента трения f _min [4] номинальный вращающий момент муфты равен:

T _ ₇p D f z ⁺ z ^{1 ( 1} C min f min )

Т = zFnRcpfmin _{X +} (_Z__XV _f .                            ⁽¹⁰⁾

min min

Считая переменной величину КУ C , приравняем друг другу правые части соотношений (9) и (10), заменив в первом из них параметр f на параметр fi — текущее значение коэффициента трения (функция времени). В результате решения составленного уравнения получим:

C = ^Z ( ^f i ~ ^f m in ) ^- ( ^{Z -} 1 ) C min f mi n ^f i ( ^{Z + Z} 1 ) ^{+ Z} 1 ^f i ^{- Z} 1 ^f m in ( 1 ^- C min f min )                    (11)

( ^{Z -} 1 ) f min f ( ^{Z + Z} 1 ) ^{- Z} 1 ( ^{Z -} 1 ) C min f min f (^f i ⁺ 1 ) ^{+ Z} 1 ^f i'      "

Соотношение (11) устанавливает зависимость величины КУ C от текущего значения коэффициента трения, при котором распорная сила УУ изменяется так, что обеспечивается постоянство суммы моментов сил трения ОФГ и ДФГ.

Величину C _min можно вычислить на основе соотношения (10) по следующему выражению:

c.

min

F n^Z R cp^fmin ( ^{Z + Z} 1 )^- T H

T H ( ^{Z -} 1 ) f mm ^{+ ZZ} 1 F n^Rcp f m²m "

Для определения характера функции (11) применим графический способ. При построении графика функции воспользуемся следующими исходными данными: R_cp = 0,1 м; z = 8; Z 1 = 2;

F n = 800 Н; f mn = 0,1; T h = 350 Нм.

При этих исходных данных величина C _min составила 0,82.

График указанной зависимости показан на рис. 2 (кривая 1).

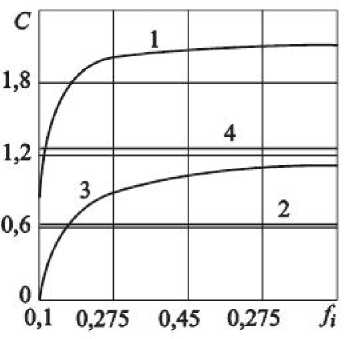
Рис. 2. Графики зависимости коэффициента усиления от текущего коэффициента трения

Из графика следует:

• -    КУ C увеличивается с ростом коэффициента трения;

• -    наибольший рост КУ C имеет место в интервале значений коэффициента трения 0,1 ... 0,275 при равных размерах частей общего интервала;

• -    при минимальном значении коэффициента трения величина КУ C равна C min .

Для принятой конструктивно-компоновочной схемы ОФГ (см. рис. 1) ограничение сверху величины КУ C имеет следующий вид [5]:

C ^ -^,                             (13)

z1fmax где fmax — максимальное значение коэффициента трения.

На рис. 2 прямой 2 показана величина КУ, построенная на основе соотношения (13) при f max _ 0,8. Расположение кривой 1 и прямой 2 показывает, что требуемые для автоматического регулирования значения КУ C (при реализации нагрузочной характеристики «идеальной» АФМ [6]) выше, чем его предельное значение. Вследствие этого реализация «идеальной» АФМ в данном случае невозможна даже при значении z 1 _ 1, когда предельная величина КУ C может быть увеличена в 2 раза.

Рассмотрим вариант АФМ второго поколения, в котором при минимальном значении коэффициента трения отрицательная обратная связь на пары трения ОФГ не действует.

Вначале рассмотрим теоретическую сторону решаемой задачи. При указанном условии номинальный вращающий момент АФМ равен:

Т н = ( z + Z 1 ) Ш .                          (14)

Уравнение, с помощью которого можно установить закономерность величины КУ C при варьировании коэффициента трения, в данном случае имеет вид:

W r +l z f rC = ( ^{z +} z 1 ) F R ■ f '

Решение этого уравнения запишем как

C _ ( z ^{+ Z} 1 ) ^{f -}( z ^{+ Z} 1 ) f mln ( Z - 1 )( Z + Z 1 ) ^f min ^{f + zf 2} .

График функции (15) приведён на рис. 2 (кривая 3). Он построен по тем же исходным данным, что и кривая 1, кроме z 1 _ 1. График предельной величины КУ C (при значении z 1 _ 1) показан на рис. 2 прямой 4.

Анализ построенных графиков показывает:

• -    КУ C возрастает по мере увеличения коэффициента трения (кривая 3);

• -    наибольший прирост величины КУ C наблюдается в интервале значений коэффициента трения 0,1 … 0,275;

• -    при всех значениях коэффициента трения (в пределах оси абсцисс) текущая величина КУ C не превышает предельное значение (кривая 3, прямая 4).

Выше теоретически обоснована возможность реализации варианта АФМ с переменной величиной КУ C , не превышающей предельного значения ни при каких величинах коэффициента трения. Рассмотрим соответствующий вариант муфты. Напомним, что в этом варианте должно быть предусмотрено C _min _ 0 .

Последнее условие выполнимо только при α = 0. Из этого следует, что распорная сила УУ при f _mln должна быть также равна нулю. Однако при увеличении коэффициента трения C * 0,

• т. е. угол должен также увеличиваться. Но увеличение угла α возможно только при действии распорной силы, что противоречит поставленному выше условию.

Таким образом, равенство C _min = 0 необходимо считать условным, т. е. при C _min ≠ 0 распорная сила УУ, действующая на пары трения ОФГ, должна отсутствовать.

Из этого следует, что при значении f _min распорная сила УУ должна действовать не на нажимной диск, а замыкаться на ведущей полумуфте.

Принципиальная схема АФМ, удовлетворяющая указанному условию, показана на рис. 3. Две соосные полумуфты 1 и 2 связаны между собой фрикционными группами, состоящими: - из дисков 3 и 4, образующих ОФГ;

• -    из дисков 5 и 6, образующих ДФГ.

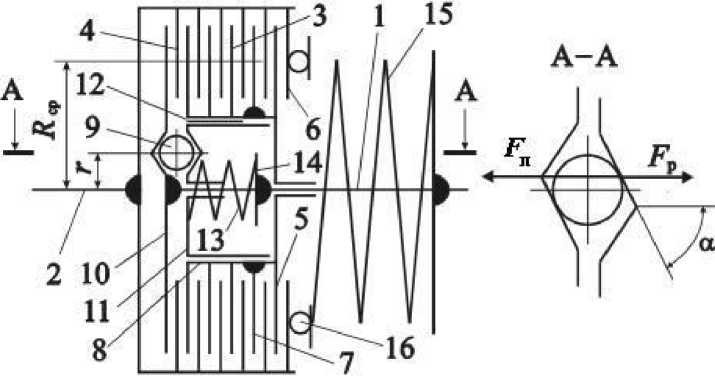
Рис. 3. Модернизированная принципиальная схема АФМ второго поколения

Фрикционные группы разделены фланцем 7 нажимного диска 8, свободно установленного на ступице полумуфты 1. Диски 3 и 5 связаны в окружном направлении со ступицей нажимного диска, диски 4 и 6 — с барабаном полумуфты 2.

Структурное построение УУ обратной связи рассматриваемой АФМ отличается от УУ базового варианта. УУ состоит из тел качения 9, которые размещены в скошенных гнёздах, выполненных в упорном диске 10, жёстко закреплённом на ступице полумуфты 1, и в опорной втулке 11, которая размещена в центральном отверстии нажимного диска 8. Опорная втулка связана с нажимным диском направляющей шпонкой 12 и подшипником к телам качения 9 пружиной 13, которая правым концом опирается на жёсткий упор 14, закреплённый на ступице полумуфты 1 (рис. 3). Пружина 13 поставлена в муфту с предварительным натяжением и вместе с упором 14 размещена в центральном отверстии опорной втулки 11.

В статическом положении АФМ, т. е. при отсутствии нагрузки, передаваемой муфтой, между правым торцом опорной втулки и нажимным диском осевой зазор может отсутствовать либо быть минимальным (~0,1 … 0,15 мм).

Общее силовое замыкание пар трения ОФГ и ДФГ в муфте осуществляется пружиной 15, которая передает усилие через упорный подшипник 16.

Идея реализации в АФМ так называемого «квазинулевого» значения КУ C _min заключается, таким образом, в силовом замыкании распорной силы на полумуфте 1 при минимальной величине коэффициента трения.

Для определения параметров УУ модернизированной АФМ запишем уравнение осевого равновесия опорной втулки 11 при минимальном значении коэффициента трения и при номи- нальном вращающем моменте, передаваемом муфтой. Перед составлением упомянутого уравнения установим действующие на опорную втулку силы:

• -    распорная сила F p.min , действующая со стороны УУ;

• -    осевая сила натяжения пружины 13;

• -    сила трения между нажимным диском 8 и направляющей шпонкой 12.

Сила трения между ступицей полумуфты 1 и опорной втулкой 11 не учитывается ввиду её незначительной величины.

На основании изложенного выше запишем уравнение равновесия опорной втулки 11 в осевом направлении:

где F_{п 13} — первоначальная сила натяжения пружины 13; F _тр — сила трения между нажимным диском 8 и направляющей шпонкой 12 (рис. 4).

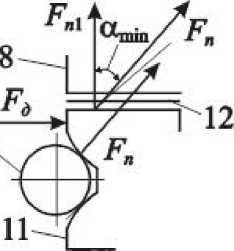
Рис. 4. Расчётная схема № 1 УУ муфты

Распорная сила F _{p . min} вычисляется по следующей формуле:

Тном p. min      r g min , где Тном — номинальный (настроечный) вращающий момент АФМ; αmin — минимальный угол давления между телом качения 9 и боковой стенкой гнезда УУ (см. рис. 4).

Номинальный вращающий момент АФМ вычисляется по соотношению (14).

Величина силы трения F _тр вычисляется по соотношению:

27"    „

F p = -^,                         (18)

где f ₁ — коэффициент трения между нажимным диском 8 и направляющей шпонкой 12; d — диаметр центрального отверстия нажимного диска.

Очевидно, что величина КУ C _min зависит от величины угла α min . Чтобы установить величину последнего, обратимся к рис. 4, на котором приведена схема, поясняющая распределение сил, действующих на опорную втулку 11 в шпоночном соединении.

Сила нормального давления между телами 9 и 11, перенесенная по правилу параллельного переноса силы, представляет движущую силу. При этом дополняющий момент силы, действующий на опорную втулку 11, не создает нагрузку, искажающую картину силового взаимодействия в шпоночном соединении и в расчёт не принимается. В противоположном направлении действует сила сопротивления, т. е. сила трения.

Для осуществления движения опорной втулки вместе с направляющей шпонкой относительно нажимного диска проекция силы нормального давления F_н на плоскость движения направляющей шпонки должна быть по меньшей мере равна силе трения.

Рассматривая расчётную схему, изображённую на рис. 4, запишем:

F -F cos | П-а I = F sin а ,(19)

д п I 2 Mmin I п

Ft = Fnifi.(20)

В выражении (19) параметр F_д — движущая сила, с помощью которой осуществляется перемещение направляющей шпонки и опорной втулки относительно нажимного диска; F_п и α min — см. выше. В равенстве (20) параметр F_{п 1} — сила нормального давления в плоскости шпоночного соединения.

Из силового треугольника найдём:

F „ 1 = F cosa_m№.                                       ⁽²¹⁾

Исходя из поставленного выше условия и воспользовавшись соотношениями (19) и (21), получим:

tga m. = f l .                                              (22)

На основе равенства (22) запишем:

Rср        Rср min r g min r 1 .

Формула (23) пригодна для вычисления величины КУ C _min .

При выполнении равенства (22) и величине КУ C _min , вычисляемой по соотношению (23), начальная сила натяжения пружины 13 может быть равна нулю: относительная неподвижность системы тел «опорная втулка 11 и направляющая шпонка 12 — нажимной диск 8» обеспечивается равенством силы сопротивления и движущей силы.

Схема, показанная на рис. 4, иллюстрирует лишь возможность реализации нулевой распорной силы при ненулевой величине C _min . Для автоматического регулирования величины распорной силы величина КУ C должна изменяться в соответствии с закономерностью, установленной соотношением (15). В связи с этим боковая стенка гнезда под тело качения УУ должна быть очерчена кривой линией, а опорная втулка 11 должна быть кинематически связана с нажимным диском 8 в осевом направлении.

Согласно схеме УУ обратной связи, показанной на рис. 4, последнее условие не выполняется, в связи с чем необходимо её изменение.

Вариант схемы УУ, удовлетворяющей поставленным выше условиям, показан на рис. 5, а . Этот вариант отличается от изображённого на рис. 4 тем, что УУ дополнено пружиной 17 (нумерация позиций элементов — согласно рис. 4), поставленной в муфту между нажимным диском 8 и опорной втулкой 11 концентрично пружине 13. Таким образом, во время трения (работы муфты) распорная сила УУ будет передаваться на нажимной диск посредством осевой деформации пружины 17. Часть распорной силы УУ будет замыкаться на ступицу полумуфты 1 посредством осевой деформации пружины 13.

Поскольку, согласно соотношению (15), значение КУ C должно увеличиваться нелинейно при увеличении коэффициента трения, боковые стенки гнёзд под тела качения УУ должны быть очерчены образующими в виде кривых линий, выпуклых по отношению к телам качения.

Следовательно, величина угла давления α i тел качения УУ должна возрастать от дна гнезда к его периферии.

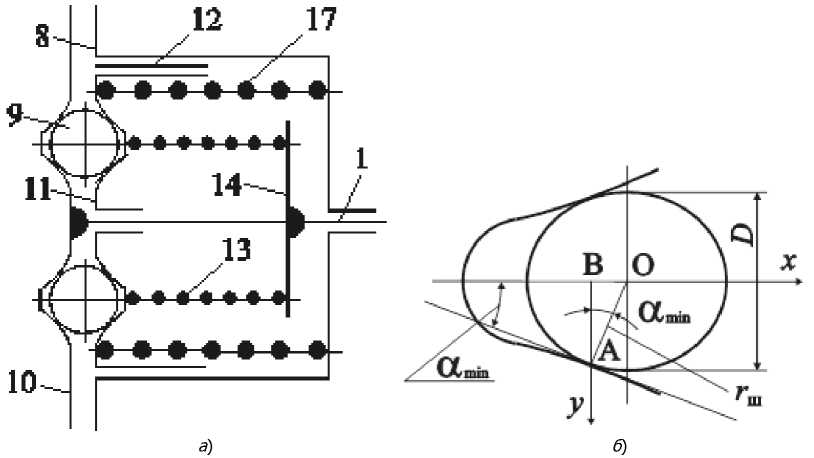
Рис. 5. Схемы УУ обратной связи: а — модернизированная; б — расчётная, № 2

Для установления формы кривой, образующей боковой стенки гнезда, запишем уравнение осевого равновесия опорной втулки 11 в системе координат x — y (где x — абсцисса координатной системы, совпадающая с осью гнезда, y — ордината системы, принадлежащая плоскости, параллельной оси вращения АФМ):

F p.i - C X i — C 2 X i — F tp = 0, (24)

где Fp. i — текущая распорная сила; C1 — осевая жёсткость пружины 13; C2 — осевая жёст- кость пружины 17; xi — текущая абсцисса, равная текущему осевому перемещению опорной втулки 11.

Текущая распорная сила УУ АФМ может быть представлена следующим соотношением:

F p.i = Т п tga i ,                                            (25)

где α i — текущий угол давления тела качения.

По условию задачи величина номинального вращающего момента АФМ должна оставаться постоянной независимо от коэффициента трения. В соответствии с этим, используя в уравнении (24) соотношения (14), (18) и (25), получим:

^{( z} + ^z 1 VAf i» ^i- C 1 + C ) x i — ^{2 (} z + ^zd^F _n R^c p f m_{m f} 1 = o.              (26)

Учитывая геометрическую интерпретацию первой производной функции, проинтегрируем уравнение (26):

( C + C ) rx 2     2 rf

y, = -r^—i— + —1 x, + C , y i 2 (z + Z1) FnRcpfm, d ' 1, где C1 — постоянная интегрирования, которую можно найти из начальных условий: yi = у0 при xi = 0 .

Из этого следует:

Ci = у о, где y0 — начальная ордината кривой.

Начальную ординату y0 можно найти, используя расчётную схему, изображённую на рис. 5, б. Согласно данной схеме начальная ордината y0 , равна длине отрезка АВ. При величине радиуса тела качения, равной rш , начальная ордината составляет:

у_ = АВ = г • cos о y 0             ш min .

Сделав замену cos а .

min

V¹ + tg 2 ^a mm ,

а также имея в виду, что (см. выше)

tW in = f i , запишем выражение (28) в следующем виде:

У 0 =

Ti+ f

С учётом полученного выражения (29) запишем соотношение (27) в следующем виде, учитывая удвоенное перемещение опорной втулки (по отношению к осевому перемещению тел качения):

( C + C ) r     ₂ 4 rf r

• У, =  --—---- X 2 + -- 1 X, + —Е=ш

i   ( z + Z i ) F n R cp f min       d i   1+

В соотношении (30) f 1 = const, как принимается на практике [7].

Профилирование боковых стенок гнёзд под тела качения УУ в соответствии с выражением (30) позволяет реализовать зависимость (15) для оптимального изменения величины КУ C в функции коэффициента трения и осуществить таким образом оптимальное регулирование с целью достижения высокой точности срабатывания исследуемой АФМ.

Результаты исследования могут иметь практическое применение при расчёте и проектировании модернизированного варианта АФМ второго поколения для определения оптимальных величин параметров и синтеза элементов УУ.

Выводы.

• 1.    Настоящее исследование вызвано необходимостью повышения точности срабатывания базового варианта АФМ второго поколения.

• 2.    Основной идеей создания модернизированного варианта АФМ второго поколения является установление зависимости КУ обратной связи от текущего значения коэффициента трения и синтеза на этой основе принципиальной схемы УУ с определением его параметров.

• 3.    При минимальной величине КУ, не равной нулю, реализация на практике «идеальной» нагрузочной характеристики АФМ невозможна, поскольку расчётное значение КУ превышает его предельно допустимую величину.

• 4.    Если распорная сила отсутствует, значение коэффициента трения минимально и КУ изменяется в соответствии с установленной закономерностью, величина КУ не превышает предельного значения. Это обеспечивает автоматическое управление с теоретически достижимой «идеальной» нагрузочной характеристикой.

• 5.    Синтезирована принципиальная схема АФМ, в которой реализован принцип, указанный в п. 4, величина КУ не равна нулю. Принцип реализован при минимальном значении коэффициента трения.

• 6.    Найдена геометрическая форма кривой, очерчивающей боковую стенку гнезда под тело качения УУ и обеспечивающей автоматическое регулирование в АФМ с целью получения теоретически «идеальной» нагрузочной характеристики муфты.