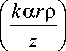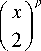Эллиптический световой пучок Гаусса-Лагерра

В последнее время вырос интерес к эллиптическим гауссовым лазерным пучкам. Так в [1] рассмотрен де-центрированный эллиптический гауссовый пучок, распространяющийся в осе-несимметричной оптической системе. Для описания такого пучка используется тензорная техника. В [2] введены в рассмотрение де-центрированные эллиптические пучки Эрмита-Гаусса. Эллиптический гауссовый пучок частичнокогерентного света исследован в [3]. Дифракция Френеля эллиптического (астигматического) гауссового пучка на дифракционной решетке рассмотрена в [4]. В [5] исследуется распространение такого пучка в одноосном кристалле, а в [6] рассмотрена генерация второй гармоники в нелинейном кристалле с помощью эллиптического пучка.

Гауссовые пучки с различной степенью эллиптичности можно использовать для выравнивания формы пучка [7], то есть для получения лазерных эллиптических пучков с однородной интенсивностью по сечению пучка. С помощью линейной комбинации эллиптических пучков Эрмита-Гаусса можно сформировать «трубчатые» (полые) эллиптические лазерные пучки на оси которых будет нулевая интенсивность [8].

В [9-13] введены в рассмотрение и исследованы теоретически [9-12] и экспериментально [13] пучки Айнса-Гаусса. Такие световые поля являются частными решениями параксиального волнового уравнения (типа уравнения Шредингера) в эллиптических координатах. В этих координатах уравнение решается методом разделения переменных, и решение получается в виде произведения гауссовой функции на многочлены Айнса. Многочлены Айнса являются решениями дифференциального уравнения Уиттекера-Хилла. Пучки Айнса-Гаусса являются ортогональным базисом, обобщающим известные модовые базисы Эрмита-Гаусса и Лагерра-Гаусса. Когда эллипс переходит в окружность (эксцентриситет s =1), то моды Айнса-Гаусса переходят в моды Лагерра-Гаусса, а при стремлении s к бесконечности (эллипс переходит в отрезок прямой) моды Айнса-Гаусса переходят в моды Эрмита-Гаусса.

Заметим, что в [14] рассмотрены похожие лазерные пучки, названные модами Эрмита-Лагерра-Гаусса, которые также при определенном значении параметра (угла поворота цилиндрической линзы вокруг оптической оси) переходят в обычные моды Эрмита-Гаусса и Лагерра-Гаусса.

Эллиптические пучки могут также быть сформированы с помощью наклонного падения осесимметричного пучка на оптический элемент.

В работах [15,16] рассмотрено наклонное падение лазерного пучка с плоским волновым фронтом на конический аксикон и бинарный дифракционный аксикон. В [15] экспериментально и численно исследовалась картина дифракции, которая образуется при наклонном падении (угол наклона 8-16 ° ) коллимированного пучка из гелий-неонового лазера на конический аксикон с углом при вершине 0,01 радиан и диаметром основания 40 мм. Было показано, что если при осевом освещении основания аксикона формируется световой бездифракционный пучок Бесселя нулевого порядка, то при наклонном падении картина дифракции теряет радиальную симметрию, пучок начинает расходиться и изменять структуру поперечного распределения интенсивности.

Аналогичные исследования были проведены в [16], но вместо обычного аксикона использовался бинарный дифракционный аксикон. Угол наклона падающего света с длиной волны 2 =632,8 нм был до 10 ° , диаметр дифракционного оптического элемента (ДОЭ) – 16,4 мм, а параметр аксикона a =0,036. Функция пропускания аксикона имеет вид exp(- ikar ), где к - волновое число, r – радиальная координата.

В [17] экспериментально и теоретически исследовалась дифракционная картина, которая получается при наклонном падении плоской волны на многоканальный бинарный ДОЭ, пропускание которого пропорционально функции, описывающей пять бесселевых пучков, распространяющихся под разными углами к оптической оси с амплитудами J m (ar )exp( imq) m =0, ±1, ±2. Было показано, что при этом формируются расходящиеся астигматические бесселевые пучки, картины дифракции которых повернуты на 45 ° вправо при m >0, и на 45 ° влево при m <0 и не повернута при m =0. Причем, чем больше номер моды Бесселя | m | , тем больше локальных минимумов и максимумов наблюдается в картине дифракции на фиксированном расстоянии от ДОЭ.

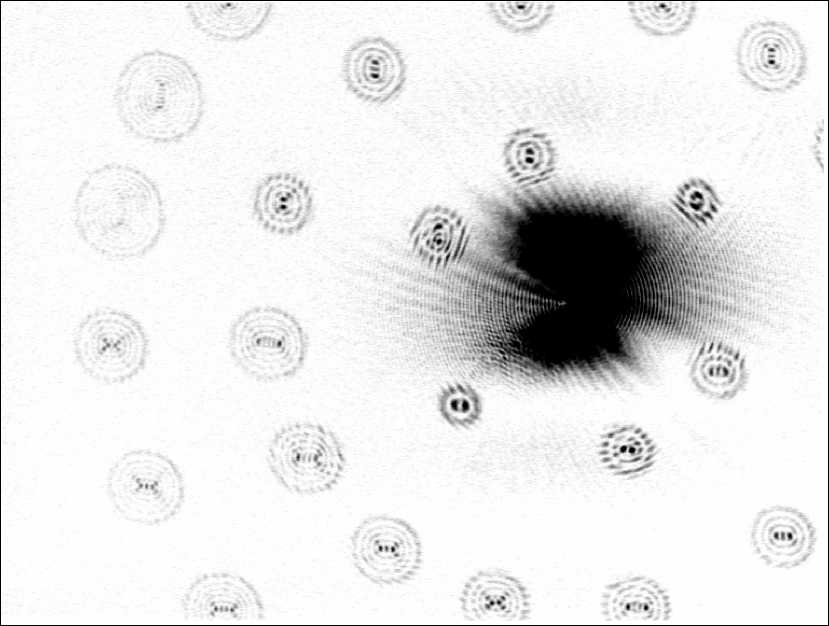
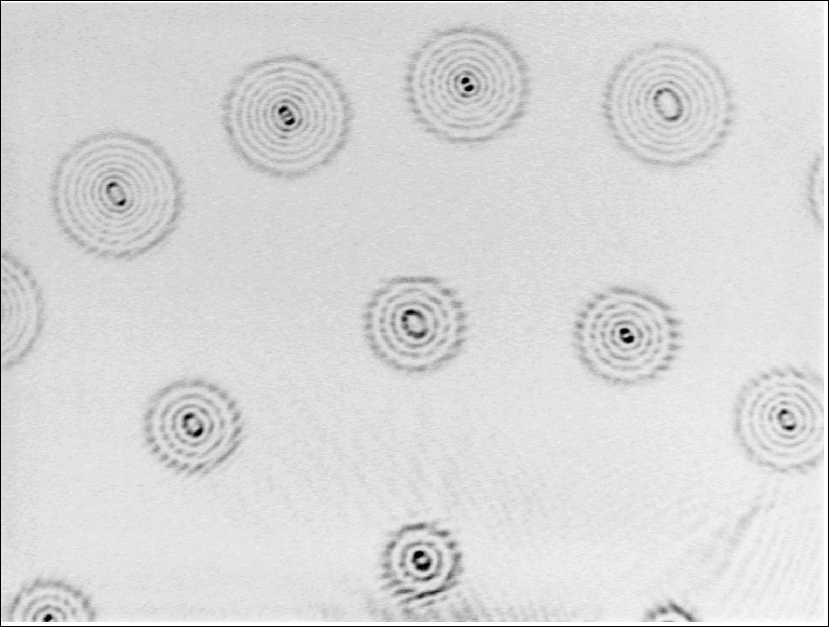
В данной работе рассматривается распространение эллиптического пучка Гаусса-Лагерра (ГЛ), который уже нельзя считать модой. Показано, что при наклонном падении плоской волны на ДОЭ, функция пропускания которого пропорциональна функции, описывающей моду ГЛ порядка ( m,n ), возникает дифракционная картина, которая тождественна дифракционной картине, формируемой эллиптическим пучком ГЛ. При распространении в однородном пространстве эллиптический пучок ГЛ формирует дифракционную картину, которая повернута на +45 ° при m >0, и на -45 ° при m <0. Причем число локальных максимумов с ростом расстояния z сначала растет, а потом убывает, и L m ( x ) при z ^да (в дальней зоне) формируется картина дифракции, состоящая из набора концентрических эллипсов, повернутых на 90 ° по отношению к исходной картине дифракции при z =0.

1. Преобразование Френеля от моды Гаусса-Лагерра

С помощью справочного интеграла [18]:

I mn ( P , z ) =^ mn ( P , 6 , z )| 2 .

С помощью светового поля вида (при z =0):

z x 2 n + m       /     2

I r I                 I r

^ m n ( r , Ф ) = I — I     exp l--- + im ф

I wn J         I wn можно сформировать обобщенные моды ГЛ, которые также будут радиально-симметричными и смо- гут сохранять свою структуру при распространении с точностью до масштаба. Используем справочный интеграл [18]:

да

J r2n+m exp (-pr2) Jm (cr) r d r = n! cm        ( c2 I rm

---_;------- exp-- L„ 2 m + 1 p m + n + 1       I 4 p J n

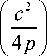
Тогда преобразование Френеля от исходного светового поля (4) с учетом (5) будет иметь вид:

^ m n ( P , 6 , z ) =

( - i ) ^{m +1} k

z

„ „⁽ ik P² , ■ a¹ exp ---- + im 6 x

I 2 z          J да m

J x ² exp( - px ) J_m ( b^x ) L m ( cx )d x = 0

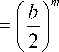
(p-c)n ( b2 ).„ — — exp--\L pm+n+1 p| 4pJ n

( b 2 c 'J ( 4 pc - 4 p ² J ,

где J_m ( x ) – функция Бесселя m -го порядка первого рода, – присоединенный многочлен Лагерра, n , m – целые числа, можно найти выражение для преобразования Френеля от моды ГЛ:

m

^ mn ⁽ r , Ф ) = — \ ^X I w) J

x exp

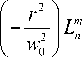
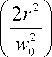
где ( r, ф) - полярные координаты, w ₀ - радиус пере-

тяжки гауссового пучка.

Используя (1) и (2) получим выражение для амплитуды моды ГЛ на расстоянии z от перетяжки:

^ mn ⁽ P , 6 , ^z )

( - i ) ^{m +1} k 2 n z

„ „⁽ ik P² , ■ a exp I + im 6

I 2 z

x

exp

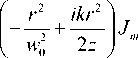
m

/ m +1 I               Л ⁿ о ¹

^{( -} i ) ^z 0 ^{n !} I 1 - ^iz 0 I ²

z I z J

x exp

где x =

x

ik P ² ----+ im 6

2 z

—2--+ w2(z)

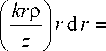
m x2 exp(-x)Lm (x),

ik

2 R ( z )

P ² , R ( z ) = z

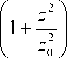
2. Наклонный параксиальный световой пучок Гаусса-Лагерра

Осветим наклонной плоской волной exp( ikr - cos ф ■sin y ), у - угол наклона к оси x = r cos( ф ), плоский оптический элемент, пропускание которого пропорционально функции, описывающей моду ГЛ T_mn ( г, ф ), радиальную часть которой обозначим:

m да / M \/

I rV2 II x ---- exp I -

01 w0 JI

r ²    ikr ^{2 1} mm

2     -    ¹ L

w ₀

2 z

n

2 r ²1 л

—2- I r d r = w o J

m

I                                    1 I                                     1 I 1

^ mn ( r ) =          exp l- — I L m l-^ I .         (7)

I ^w 0 J I ^w 0 J I ^w 0 J

w (pV21i 0          exp w (z) I w (z) J

-p ²      ik P ²    .

—— +--+ im 6 - w2(z) 2R(z)

Тогда преобразование Френеля от моды ГЛ (2) при наклонном освещении будет иметь вид:

F., ( P , 6 , z ) =

( - i ) ^{m +1} k

-— ---x

z

- i (2 n + m + 1)arctg — I z 0.

Г m ( . '1

L n I 2/ \ I, ( ^{w ( z} ) J

z                     I       z. I где w(z) = w0 1 + —, R(z) = z I1 + -°- I, z0

z ₀

z

kw 0²

₂ , k

x exp

ik P² , ■

----+ im arctg 2 z

P sin 6 z sin у-P cos 6

да

П A I ikr 1 T ^x|^ mn ⁽ r ^)exp | — I J m 0 I ² z J

x

– волновое число света.

Из (3) видно, что структура моды ГЛ сохраняется и интенсивность является радиальносимметричной функцией:

I kr /2-2 ”4 x| — zz sin y + p

I z

- 2 p z cos 6 sin y | r d r .

В полярных координатах с наклоном:

^ = р cos 9- z sin y ,

П = р sin 9 ,

аргумент функции Бесселя в интеграле уравнения (8) будет зависеть только от радиальной составляющей:

c ² + n 2 = z 2 sin ² Y + р ² - 2 р z cos 9 sin y .         (10)

То есть из ур.(8) с учетом (9) и (10) следует, что интенсивность наклонной параксиальной моды ГЛ будет радально-симметричной:

I y G² + n 2 , z ) = F y ( P , 9 , z )| 2 . (11)

Чтобы наклонное падение освещающего пучка привело к искажению моды ГЛ требуется рассмотреть напараксиальное распространение света, то есть от преобразования Френеля перейти к преобразованию Кирхгофа.

Преобразование Кирхгофа от наклонного пучка ГЛ имеет вид:

F ( e , П , z ) =

—ik И хи X л exP(ikR) я я , P ^ mn ( x’ У )----n---d x d У 2П               R где R2 = (e - x)2 + (n- У)2 + z2.

В полярных координатах (12) примет вид: • i да 2л

^{F (} P , ⁹ , z ) /.IP mn ⁽ r , Ф ) ^X

^{2 n z} b 0

x exp

’r ² + p ² + z ² - 2 r р cos( 9 - ф ) ] r d r d ф ,

где R ® z в знаменателе (12).

Тогда непараксиальное распространение наклонного пучка ГЛ будет описываться выражением:

F, (P, 9, z) = ik да 2 л

=---ffv _mn ( r , ф )exp [ ikr cos ф sin y +   .     (14)

^{2 n z} о 0

+ ik^r ² + p ² + z ² - 2 r p cos( 9 - ф ) 1 r d r d ф

Предположим, что z >> r и z>>p и разложим квадратный корень в показателе экспоненты в (14) в ряд Тейлора:

z ² + r ² + р ² - 2 r р cos( 9 - ф )

r ² + р ² - 2 r р cos( 9 - ф )

2 z

r ⁴ + р ⁴ + 2 r ² р ² - ( 4 r 3 р + 4 r р ³ ) cos( 9 - ф ) + 4 r ² р ² cos ² ( 9 - ф )

8 z ³

r ⁴

Пусть в уравнении (15) —3 <<  z , 8 z

4 r ³р

—7" <<  z и 8 z ³

4 r р³        „               ,,

—— <<  z . Тогда вместо (15) получим:

8 z

4z ² + r ² + р ² - 2 r р cos( 9 - ф ) ®

2      4 Л Л 2

р р I J r I ⁺ I

2 z 8 z ³ J [ 2 z

-

r 2р2

2 z ³

-

—- cos(9-ф) - —3-со$2(9-ф).

С учетом (16) вместо (14) получим:

-i

F Y ⁽ р , ⁹ , ^z ) = /"exp ^ik | ^z + — „ 2 n z       I     2 z 8 z

ik

р ⁴

да Л

X

2 п z

ikr

: J ^ mn ( r )exp ---- 1 1

n                 2 z I

' 2л

-

р ²

2 z

X

X

X

2л

С                          •       ikr р     z_A ,

I exp im ф + ikr cos ф sin y --cos( 9-ф )

n                                  z

-

ikr ²р²                       I ,

^- F cos2( 9-ф ) d ф| r d r .

Перепишем интеграл по ф в фигурных скобках в ур. (17) отдельно в виде:

1 ₀ = exp( im 9 ) x

2л

X

г             ikr р„ exp imф--°cos(^-v)

J                  7

z

-

ikr ²р²        1

---т— cos2 y d ф , 4 z ³

где

Ф = ф-9 ,

‘ р 0 = ( р- z sin Y cos 9 ) 2 + ( z sin y sin 9 ) 2 ,

I    z sin y sin 9

v = arctg |----------------

(р- z sin y cos 9

Обозначим в (18):

P = ir e . , q = kr ;,,; z         4 z

.

.

Тогда интеграл (18) примет вид:

2л

1 ₀ = exp( im 9 ) J exp [ im ф-

- iP cos(ф-v) - iQ cos2ф] d ф = да

= exp(im9) E iPJp(Q)x p=-да

2л xJ exp [ i 2 p ф + im ф-iP cos(ф-v)] d ф =

= 2n(-i)m exp[im(9 + v)] x да

^X E ⁽ - i ) p ^J p ^{( Q} ) ^J m +2 p ^{( P )e}xp⁽ i ² P ^{V )}.

p =-да

Отметим, что такое же выражение, как (21), было получено в [3] для описания астигматического бес-селевого пучка.

С учетом (21) амплитуда светового поля (17), описывающего астигматический пучок ГЛ (по аналогии с астигматическим пучком Бесселя [3]) примет вид:

l ( P , 6 , Z ) =

- ik     ikp /    2 a 2-2

=---exp ---- ( cos 6 + a sin

2 n z      2 z '

6) x

( - i ) m ⁺1 k

F ( P , 6 , z ) =-------- exp ^x

z

да 2п л xj J Tmn(ar)expl imФ + o o                       _

ikr ²

--- a cos ф + 2 z

I      P im(6 + v) + ik\ z +

I      2 z

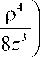
. 2 \ ik a r p    _ J . .

+ sin ф)со$(0-ф) r d r dф,

x £ ( - i ) p exp( i 2 p v^T mn ( r )exp p =-”                   0

ikr ²

x

2 z

где T mn ( r , ф ; a ) = T mn ( a r ) exp( im ф ).

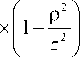
' I k V )    I kr^p)

p I 4 z ³ J J^{m +2} p [ z J r d r .

Из ур. (22) видно, что астигматический пучок ГЛ не является радиально-симметричным и не сохраняет свою структуру при распространении, т.к. азимутальный угол 9 входит в подынтегральное выражение в ур. (22) в р и v (см. (19)).

3. Эллиптический параксиальный пучок Гаусса-Лагерра

Покажем, что если заменить наклонный пучок ГЛ на эллиптический, то выражение, аналогичное ур. (22), можно получить с помощью преобразования Френеля, а не Кирхгофа. То есть, параксиальный эллиптический пучок ГЛ также не будет сохранять свою структуру и потеряет эллиптичность в зоне дифракции Френеля.

Эллиптический пучок ГЛ при z =0 описывается выражением:

m

1 2 x ² ₊ 2 _а 2 v ² )

^T mn ^{( x} , У ; ^{a )} = l-------- 2------ I ^x

I        w„       J

( x ² + a ² у ² W 2 x ² + 2 a ² у ² )

^x exp l--I L m I|^x

I      W o     JI     W o      J

x exp

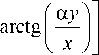
В эллиптических координатах:

x = ar cos ф, у = rsinф, 0

вместо (23) получим:

m

^Tmn^(r, ф;^a)= ------ ^x

I   Wo   J

I a²r² 'l 12a²r²^

x exp lI im lI exp(imф).

I    Wo J I w_nJ

При а=1 выражение (25) совпадает с выражением (2).

Преобразование Френеля в эллиптических координатах (24) для пучка (25) примет вид:

В ур. (26) использованы эллиптические координаты в плоскости z>o, повернутые на 9o° по отношению к координатам в плоскости z=0:

^ = p cos 6, П = ap sin 6.

Выделим в ур. (26) интеграл по углу ф;

^Fa⁽P, ⁶, z) = -^ik exp 2nz

ik^- (cos²6 + a²sin²6)

2z

x

да л

x

ikr²

JTmn(ar)exp ---(1 + a²)

^o                     4 z ^v

x

x

‘2n

²n               ikr 2 7.             .

J exp imф—4— (1-a²)cos2ф

ik^r^cos(6-ф) dф[rdr. z                         I

Выпишем отдельно интеграл по ф в фигурных

скобках в ур. (28):

л      2л

Т С „ ■       ikr²

Io = j exp imф- —— (1 -a )cos2ф

ik arp             ,

-----C^os(6-ф⁾ dф.

z

Интеграл (29) с точностью до обозначений и сомножителя перед интегралом совпадает с выражением (18). Введем обозначения:

, karp „ kr²(1 -a²) A =----, B =---------- .

z            4z

Тогда вместо (29) получим: л         ^да

Io = £ (-i) ^p Jp (B) x p=-да

2л xj exp[i2pф + imф-iAcos(ф-6)]dф = да

= 2n£ (-i)p + mJp (B) Jm+2p ( A) x p =-да x exp[ i (m + 2 p )6].

Видно, что ряды в выражениях (21) и (31) совпадают с точностью до обозначений. Окончательно из (28) и (31) получим выражение для дифракции Френеля эллиптического пучка ГЛ:

F (p, 9,z) =       k x

z

ik^pI 2 _A 2-2 x exp —— (cos 9 +a sin

9) x

да x ^ (-i)p exp[i(2p + m)9]x p=-да

да л

x

ikr²

: Jt mn (ar )exp —— (1 + a²)

^{x J}p

kr²(1 -a²)

4 z

x

^Jm+2 p

r d r.

Заметим, что при а=1 уравнение (32) совпадает с ур. (3) для преобразования Френеля моды ГЛ. Действительно, при о=1 все слагаемые ряда по p, кроме p=0, будут равны нулю, т.к. J_p(0)=0 при p*0, а J0(0)=1.

r² ,, rР

Заметим также, что при z^да так, что — << —, zz вместо (32) получим преобразование Фурье от эллиптического пучка ГЛ:

F_a (p, 9, z ^ да) « ' i'—k exp(im9) x

z да

W I krap I J x T mn (ar) Jm | ----- I r d r =

*                       \ 7 )

0              V z V

m

= (-i) m (-1) n

x

^Jp⁽x⁾=

Г( p +1)’

x ^ 0,

где r(p +1) - гамма функция, p>0. Если p<0 то надо воспользоваться равенством J_-p(x)=(-1)pJp(x), если p - целое.

Тогда интеграл в выражении (34) можно представить в виде:

Fa (p = 0, z)~ Г-¹

m

/             \   да

I aV²I Г 2rn x ---- r exp

V W ) n

x Lm

12a²r²

I 2

V W0

r d r.

m k(a² -1)1² —------ x

8 z

a²r²   ikr²(1 + a²)

w2       4 z

Используя справочный интеграл [1]:

J xm exp(-px)Lm (cx)d x =

Г( m + n +1) (p - c) n

=        n! pm+n+1        , для интеграла в выражении (36) получим:

да 2

J^{r ex}p ^-0

a r

7" wn

ikr2 (1 + a2)" ------------ x

4 z

I p²I   I 2p²1

^xexp|--2 II,

V о V , о )

( 2a 2r2A ar x Ln II r d r =

V wn )

2z      2          | П I где о = -—, p = ^ +1 — 1 .

kw0           Va )

Из (33) видно, что эллиптический пучок ГЛ при z=0 в дальней зоне дифракции при z^да опять принимает эллиптическую симметрию, но оказывается повернутым на 90° по отношению к пучку при z=0.

При конечном z эллиптическая симметрия пучка ГЛ пропадает. При конечном z в центре картины дифракции (р=0) для эллиптического пучка ГЛ с четным m=21*0 интенсивность будет отлична от нуля, хотя при z=0 и z^да интенсивность в центре пучка при р=0 равна нулю. Действительно, при р=0 все слагаемые ряда в (32) равны нулю, кроме слагаемого с номером p=-m/2, т.к. J_m+2p(0)=J₀(0)=1. Тогда из (32) для четных m=21 получим:

да л

Г(m + n +1)(-1)ⁿ exp [i(2n + m + 1)n]

2 n!

a⁴

+

W1

k²(1 + a²)² 16z²

m+1          ,

где n = arctg

k (1 + a²) w2 4 za²

Fa (p = 0,9, z) ~ J Tmn (ar) x

. 2

ikr2\ T x exP "зН1 + a ) Jm

4 z        J J

kr-(1 -a²) rdr, 4 z^V       '

. 2

где символ ~ означает пропорциональность.

При малой эллиптичности пучка а-^1, функцию Бесселя в (34) можно заменить приближенным выражением:

Из (38) видно, что модуль интеграла (38) всегда отличен от нуля. Только при а=1 из (36) следует, что поле F_a (p = 0, z) =0. Таким образом мы показали, что даже малая эллиптичность моды ГЛ нарушает условия, при которых в центре пучка при р=0 при любом z имеется ноль интенсивности. Но вихревой характер светового поля при наличии эллиптичности не изменяется, а фазовая сингулярность в центре порядка m=21 «распадается» на p сингулярностей с m/p номерами (порядками), и p точек нулевой интенсивности возникают вблизи центра пучка. Число p зависит от степени эллиптичности. Как будет показано ниже при слабой эллиптичности p=2 и под углом 45° появляются два нуля интенсивности m/2-го порядка. Для нечетного m=21+1 в центре картины дифракции (р=0) всегда остается ноль интенсивности.

Рассмотрим особенности распространения эллиптического пучка ГЛ при слабой эллиптичности (о2®1). Под интегралом в уравнении (32) заменим функцию Бесселя порядка p на приближенное выражение (35). Это возможно, во-первых, потому что аргумент функции Бесселя стремится к нулю при малой эллиптичности, а во-вторых, хоть интеграл в (32) и имеет бесконечный верхний предел интегрирования, но гауссовая экспонента, входящая в моду ГЛ, ограничивает область интегрирования конечным эффективным радиусом моды. Тогда вместо (32) запишем:

ражении (39) только слагаемые c p>0 (предполагаем, что m>0), и учтя слабую эллиптичность пучка ГЛ, сохраним только первые два слагаемых (s<<1):

^да1 V2ccf)     2.г²и?А

F_1(p,0,z)«S(p,0)jl^ar I Lm         ■ о V w> I V w0 J

xexp

2_2 r a ^w0²

ikr² (1+a²)" ----------- x

4z

F„^i(p, 0, z) * S(р, 0) x

xZ (-i) p If p—-да V2

m да

p

I Г '(p| + 1)exp(i2p0) 5(p) х

г ary 2     2ipi x ------- r 1 1 exp

^Jо V w0 J

2 2

a r

2"" w_n

ikr²(1 + a²)"

------------ x

4 z

| 2a2r2 I r     f karpl , x M---H Jm+2 p I----I r d r,

V Wo J V z J

где

. I¹, p ^ 0,

51 p) =l(-1)p, p < 0, s (p, 0)=x z x exp im0 + k- (cos2 0 + a2sin2 0)

,

k (1 -a²)    .

s =-------<< 1 - малый параметр.

4z

Заметим, что в ур.(39) слагаемые с положительными и отрицательными номерами p дают различный вклад в общую сумму. Если m>0, то в ур. (39) слагаемое с p >0 будет иметь сомножитель exp[i0(m + 2p)]rm'2pJm+2p (x), а слагаемое с p<0 -другой                           сомножитель exp[i0(m-2|p|)]rm+2pJm-2|p (x). Видно, что в первом случае (p>0) в сомножителе показатель степени радиальной переменной совпадает с порядком функции Бесселя. И наоборот, при m<0 вклад в сумму в (39) будут давать слагаемые с p<0.

Справочный интеграл из [1]:

да m+p

J x²expicx)Lm⁽cx)Jm+p (b4x) d x =

/ xn / 7 \ m f 7 2 Л f 7 2 Л

-(p - c) f b_)        b I mm I bc I exp pm+n+1 V 2 J PV 4 p J n V 4 pc - p2 J

косвенным образом подтверждает эллиптичность: только при равенстве показателя радиальной переменной x=r²и порядка функции Бесселя происходит самовоспроизведение видоизмененного пучка ГЛ.

Хотя в прямую применять интеграл (42) к расчёту (39) нельзя, так как показатель экспоненты в интеграле (39) отличается от аргумента присоединённого многочлена Лагерра. Таким образом, оставляя в вы-

[ _T f karp) isr²_i2e. f karp)     ₂ 1

x) Jm II-e Jm+21---- I+°(s2)rrdr, l z I 2             \ z / где О(^) - это слагаемые порядка малости ^ ше.

Известен ряд [15]:

и вы-

да

Z p—0

2p t   ^m+2 p

(2 p)!

m

^(x) 1

— — — x

!         2

m

■²J_m (V x²- 2 tx) x

x) (x - 2t) ²+ (x + 21)

m

-

.

Предположим, что t<<1, тогда вместо (44) можно приближённо записать:

t2pJ     (x)

Z     m+2 A ) ^ Jm (x) + Jm+2(x) + O(14).(45)

p"0   (2 p)!2

Сравнивая выражение в фигурных скобках в (43) с правой частью (45) и с учётом (44), получим вместо (43):

^f "x/Iclf)      ²r^o3

F_M 0, z) « S'(p, 0)j p^r Lm IpL ^J0 V ^w0 I V ^w0

x exp

xj

m

где

r²a² w0

ikr² (1 + a²)" ----------- x

f Vi²

I kap 1 r_x I----------I

V v z J

4 z

—1

— i0fkap) ■ i^fe I I

V z J

m

S‘(p, 0) — S(p, 0)1 fM²x

2 V z J

If kap x 1 I --------

IV z

- m

-sе^{ю) 2}

z

r d r,

- m i 0)2 - i s e0 I

.

Из уравнения (46) видно, что при р^-r выражение (46) переходит в уравнение (3) для преобразования Френеля от моды ГЛ:

F«^1(P^*, 0 z) ~ m rfV2"ar1    f2r2a21

® S (p, 0) ------ Ln I ---— Ix ww

x exp

r ²a² w²

ikr²(1 + a²)"

------------ x

_T fkapr) , ^{x J}m I ------- | r^dr,

V z J

4 z

которое вычисляется с помощью справочного интеграла (1).

Уравнение (47) показывает, что для слабой эллиптичности пучок ГЛ на периферии ведёт себя как обычная мода ГЛ, но с эллиптической симметрией, то есть картина дифракции представляет собой набор не концентрических колец, а эллипсов. В центральной части картинны дифракции эллиптического пучка ГЛ при малых р, как следует из уравнения (46), изолированные нули интенсивности будут располагаться в тех точках, в которых обращается в нуль аргумент функции Бесселя в уравнении (46):

iп p =    Z-(1 -a2)e1 4J.                         (48)

a V k

Из (48) следует, что два действительных нуля m/2-го порядка интенсивности лежат на прямой

0=л/4 на расстоянии от центра р=0 равном:

Ро

£ -(1 -a²) a\ k

Из (49) видно, что чем больше эллиптичность пучка (1-α²) и расстояние от перетяжки z, тем больше р0 и тем дальше нули интенсивности располагаются от центра р=0.

Заметим, что из (46) следует, что при ρ=0 также будет ноль интенсивности, но это не так. Дело в том, что уравнение (46) не учитывает слагаемые в уравнении (39) с отрицательными ρ<0 , которые при α ≈1 малы, но не равны нулю. Ранее было доказано, что главный вклад в значение интенсивности эллиптического пучка ГЛ определяется слагаемым вида (34), которое всегда отлично от нуля при конечных z.

Чтобы понять физический смысл того, почему при ->0 появляются два нуля интенсивности вблизи р=0 и на линии 45°, представим интенсивность эллиптического пучка ГЛ в виде интерференции двух полей.

Из уравнения (43) следует:

|F ЛР8 -)|2 ”

ности не обладает ни радиальной, ни эллиптической симметрией. Интеграл (51) может быть вычислен с помощью уравнения (1). Из (50) также видно, что с ростом z вклад второго слагаемого уменьшается и при z→∞ вместо (50) получается (33), то есть эллиптический пучок ГЛ, повернутый на 90⁰по отношению к входному пучку ГЛ при -=0. Из (50) следует, что два световых поля F₀(р) и F₁(р) сложатся в «фазе» на линии 0=-л/4. Если бы мы рассмотрели разложение (39) при m<0, то получили бы уравнение аналогичное (50), но два световых поля F₀(р) и F₁(р) складывались бы в «фазе» при 0=л/4. То есть эллиптический пучок ГЛ при своём распространении имеет такую дифракционную картину в своём сечении, которая позволяет определить левую (m<0) или правую (m>0) «закрутку фазы» имеет исходный пучок ГЛ при z=0. Причем поворот картины дифракции на угол ±п/4 в зоне Френеля не зависит от величины номера |m|. В дальней зоне дифракции эллиптический пучок ГЛ поворачивается на ±90° по отношению к исходному, и уже нельзя отличить направление вращения и знак номера ±|m|.

Заметим, что при стремлении параметра эллипса а к нулю эллиптический пучок ГЛ (23) при -=0 переходит в пучок, который изменяется только по оси x, а по оси y амплитуда остается неизменной:

m

22   22

xxx

^ mn⁽x) = \ — I ^exP\--2 I Ln\ — I.        ⁽⁵³⁾

V wo ) V w0 ) V w0 )

В дальней зоне дифракции пучок ГЛ (53) перейдет в одномерный вдоль оси ^ пучок Гаусса-Эрмита. Действительно, используя справочный интеграл [18]:

L^mm (ct) exp (p4t) d t =

« F0(p)

-

ik (1 -a²)

8z

e"F1(P) ,

n!

где

m m Ln

m+1

m n+

2 2c x Hn+m

xexp

xexp

r²a^{2   ikr 2}(^{1 + a}2)

_w02        _4z

_T fkaprI , Jm\------I r d r,

V - )

Am

F(p) = k JI ¹ I r²Lm ^- 0 V ^w0 )

r ²a² ikr²(1+a²)

_w02       _4z

^Jm +2

Из (50)-(52) видно, что структура картины ди-

фракции пучка ГЛ со слабой степенью эллиптич-

получим для амплитуды светового поля в фокусе сферической линзы следующее выражение:

Lmm (ct) exp (p4t) d t =

n!

i nm

m n+ 2²

m+1

c²

^xHn+m

получим для амплитуды светового поля в фокусе сферической линзы следующее выражение:

да

^kA [^ mn⁽x )exP -k ( x^{i +}У П) ^dx^dУ = 2ⁿf              L f J

2f где д(п) — о-функция Дирака, о =--радиус га-kw0

= (-i) m+1 5(пР^-тх

2 m + n-1

x exp

if

O J

r |3 U Ш

n + m I        I n I I,

I OJ    I O J

уссового пучка в фокальной плоскости линзы с фокусным расстоянием f.

Примеры изменения картины дифракции эллиптического пучка ГЛ показаны в последующих разделах.

• 4.    Результаты численного моделирования распространения эллиптических пучков Гаусса-Лагерра

  

  z=0 мм

  
  
  

  z=500 мм

  
  
  
  
  
  

  z=2000 мм

  
  
  

  z=4000 мм

  
  
  
  
  
  

  z=«

  
  

Рис. 1. Распространение моды ГЛ (5,2) с эллиптическим искажением в свободном пространстве (негатив). Размер изображения 5x5мм, 256x256 отсчетов. Характерный гауссовский радиус пучка σ=0,391мм, длина волны

X=0,63 мкм, коэффициент эллиптичности а=0,66

По картинам интенсивности на рис. 1 можно проследить справедливость теоретических выкладок: по мере формирования светового пучка за ДОЭ он приобретает наклон в 45⁰, а в дальней зоне наблюдается поворот всей картины на 90⁰. По мере увеличения расстояния z, количество локальных максимумов сначала растёт, а потом начинает убывать, как и было предсказано. Кроме того, видно, что при конечном z в центре картины дифракции нет нуля интенсивности, а два нуля интенсивности возникают вдоль линии под углом в 45⁰.

z=0 мм

z=500 мм

z=1000 мм

z=4000 мм

z=8000 мм

z=2000 мм

z=∞

Рис. 2. Распространение моды ГЛ (2,2) с эллиптическим искажением в свободном пространстве. Коэффициент эллиптичности α=0,66

Картина распространения моды ГЛ (2,2) также подтверждает теоретические выводы. Мы имеем 2 предсказанных локальных минимума вблизи центра изображения также, как и в случае моды ГЛ (5,2) на рис. 1. И также в центре картины при z≠0 нет нуля интенсивности.

z=0 мм

z=1000 мм

z=2000 мм

z=8000 мм

z=∞

Рис. 3. Распространение моды ГЛ (3,–1) с эллиптическим искажением в свободном пространстве. Коэффициент эллиптичности α=0,66

Поведение светового пучка изображенного на рис. 3 (моды ГЛ (3,–1)) в целом аналогично рисункам 1 и 2, с той лишь разницей, что мы имеем лишь один центральный локальный минимум, т.к. индекс моды m=–1. Кроме того, в данном случае наблюдается поворот на –45⁰в серединной области распространения.

z=0 мм

z=500 мм

z=1000 мм

z=4000 мм z=8000 мм

z=2000 мм

z=∞

Рис. 4. Распространение моды ГЛ (2,0) с эллиптическим искажением в свободном пространстве. Коэффициент эллиптичности α=0,66

Интересным примером является распространение моды ГЛ (2,0). При этом не наблюдается появления локальных минимумов в центральной части, однако видны любопытные эффекты в первом кольце моды. При m=0 центральная часть картины подвергается наибольшей трансформации (приобретает вид квадрата) на расстоянии Френеля близком к z0 ≈ 1000 мм. Внешние кольца при этом вместо эллипсов остаются окружностями. Похожий эффект наблюдается при уменьшении величины эллиптического искажения (см. рис. 5). Тем не менее, эффект поворота изображения на 90⁰в Фурье-плоскости по-прежнему проявляется в неизменном виде.

z=1000 мм

z=0 мм

z=8000 мм

z=2000 мм

Рис. 5. Распространение моды ГЛ (5,2) с эллиптическим искажением в свободном пространстве. Коэффициент эллиптичности α=0,91

z=∞

На рис. 5 показано распространение моды ГЛ (5,2) с малым коэффициентом эллиптичности α=0,91. При этом количество локальных минимумов-максимумов значительно уменьшается. Остаются лишь 2 центральных локальных минимума, которые позволяют определить индекс моды m=2. Как видно из представленных картин моделирования распространения мод ГЛ, количество околоцентральных локальных максимумов-минимумов зависит от порядков (n,m) мод ГЛ и от величины коэффициента эллиптичности. Таким образом, их число варьируется при изменении степени эллиптического искажения, т.е. угла наклона ДОЭ для одних и тех же мод ГЛ.

• 5.    Результаты эксперимента по формированию астигматических пучков Гаусса-Лагерра

Для проведения экспериментов с астигматическими пучками ГЛ использовался многопорядковый дифракционный оптический элемент (ДОЭ), согласованный с 42 модами ГЛ. ДОЭ был изготовлен по технологии электронной литографии на технологической базе Университета Йоенсуу (Финляндия). Вид фазы ДОЭ, схема соответствия номеров мод дифракционным порядкам и расчетное распределение интенсивности в фокальной плоскости линзы приведены на рис. 6. Параметры ДОЭ: бинарный микрорельеф имеет высоту 692 нм, оптимальную для излучения с длинной волны 633 нм, диаметр – 10 мм, шаг дискретизации – 5 мкм.

ДОЭ, представленный на рис. 6 формирует в симметричных дифракционных порядках моды ГЛ с одинаковыми индексами и противоположными знаками «сингулярности». Определить знак и порядок «сингулярности» моды можно повернув ДОЭ на некоторый угол относительно оптической оси. Так, на рис. 7 можно видеть экспериментально зафиксированную картину распределения интенсивности на расстоянии около z=400 мм от ДОЭ, повернутого относительно оптической оси, при освещении его коллимированным излучением гелий-неонового лазера (длина волны 633 нм), ограниченным круглой диафрагмой. На рис. 7 можно видеть, что моды, имеющие разные знаки сингулярности, «вытянулись» во взаимно-перпендикулярных направлениях. На рис. 8 показана аналогичная картина только несколько подробнее (менее сходящийся освещающий пучок и меньший наклон ДОЭ). Видно, что при небольшой степени астигматизма «развал» на отдельные нули происходит для пучков с невысоким порядком сингулярности (|m |=1,2). Для |m |>3 центральное кольцо хоть и деформируется, но еще не «дробиться» на отдельные нули.

На рис. 9 можно было проследить как при увеличении наклона ДОЭ мода ГЛ (n,m)=(5,4) постепенно трансформируется к виду очень близкому к модам Гаусса-Эрмита.

(6,6) i

(5,-1 )•

(6.4)

(6.5)

(5.-2)

(в)

(6.1)

(6,2.^

(6,3)

(3,2)

(4.-4) •

(4.-3)

(5.-3)

(3.3)

(2,2)

(4.-2)

(2.1)

(4,-1)

(5.5)

‘            (5.4)

(4,1)             -»(5.3)

"       (4.2)       \

(1.1)

.•'(2.-2)

(3,-3)

(4.3)

(5.2)

i (4.4)

(3.-1)

(5,1)

• (6,-6)

(6.-5)

(6.-4)

/ ' (6.-3)

(5.-4)

(б)

.__________,„-"""(6.-2)

(5.-5)      (6,-1)

Рис. 6. 42-порядковый бинарный ДОЭ, формирующий моды ГЛ: фаза (а), схема соответствия номеров мод дифракционным порядкам (б), расчетное распределение интенсивности в фокальной плоскости линзы (в).

Рис.7. Экспериментальное распределение интенсивности (получены в сходящемся освещающем пучке) при наклоне ДОЭ относительно оптической оси.

Рис.8. Экспериментальное распределение интенсивности (получены в сходящемся освещающем пучке) при небольшом наклоне ДОЭ относительно оптической оси.

Рис.9. Экспериментальное распределение интенсивности для моды ГЛ (n,m)=(5,4) при различных углах наклона ДОЭ относительно оптической оси.

Рис 10. Экспериментальные распределения интенсивности при угле наклона ДОЭ относительно оптической оси, близком к 75°.

Из рис. 10 можно видеть, что при сильном наклоне ДОЭ моды ГЛ принимают вид мод Гаусса-Эрмита. При этом соответствие номеров мод следующее:

nGH nGL, mGH = nGL + |mGL |

Заключение

В работе аналитически и численно исследовано распространение параксиального эллиптического пучка Гаусса-Лагерра. Показано, что если в начальной плоскости сечения пучок имеет структуру в виде софокусных эллипсов с нулевой интенсивностью на оптической оси, если номер m спиральности (или сингулярности) фазы пучка отличен от нуля, то при распространении в зоне дифракции Френеля в центре пучка на оптической оси интенсивность будет отличаться от нуля.

При этом фазовая осевая сингулярность m-го порядка «распадается» на p сингулярностей m/p-го порядка и вблизи осевой точки в сечении пучка возни- кают p нулей интенсивности. Число нулей p зависит от степени эллиптичности пучка а. Так, при малой степени эллиптичности (1-α2) << 0 комплексную амплитуду пучка можно эффективно представить в виде суперпозиции двух слагаемых, которая приводит к появлению двух (p =2) нулей интенсивности m/2-го порядка сингулярности при четном числе m. Эти нули «лежат» в сечении пучка на прямой линии, составляющей с осью x угол в +45° при m>0 и -45° при m<0. С увеличением степени эллиптичности пучка растет число слагаемых в суперпозиции и число p изолированных нулей интенсивности. При дальнейшем распространении пучка вдоль оптической оси слагаемые в суперпозиции, зависящие от расстояния как z"q, q=0, ±1, ±2, ... , будут давать все меньший вклад в общую сумму, и при z^» (дальняя зона) сформируется пучок ГЛ с эллиптической симметрией m-го порядка сингулярности с нулевой интенсивностью на оптической оси, сечение которого тождественно сечению исходного пучка (при z=0) , но повернуто по отношению к нему на 900.

Численные и натурные эксперименты подтвердили теоретические выводы. На основе численного моделирования показано как видоизменяется картина дифракции эллиптического пучка ГЛ на различных расстояниях при одинаковой степени эллиптичности. При проведении экспериментов распределение интенсивности пучка ГЛ фиксировалось на одном и том же расстоянии, по при различном наклоне ДОЭ к оптической оси. При этом можно было проследить как при увеличении наклона ДОЭ моды ГЛ постепенно трансформировались к виду, очень близкому к модам Гаусса-Эрмита.

Работа выполнена при поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (BRHE), грантов Президента Российской Федерации МД-209.2003.01 и НШ-1007.2003, а также гранта РФФИ 05-01-96505.