Эмпирическая идентификация типологических траекторий динамики временного ряда

Автор: Крюков П.А., Крюкова В.В.

Журнал: Форум молодых ученых @forum-nauka

Статья в выпуске: 6-2 (22), 2018 года.

Бесплатный доступ

В статье рассмотрены основные статистические критерии проверки временного ряда на наличие тренда. Для временного ряда валютного курса инструмента EUR/USD выполнена эмпирическая проверка динамики поведения валютного курса на часовых данных. Предложен авторский метод эмпирической идентификации типологических траекторий динамики валютного курса. Приведены результаты, которые могут быть использованы для построения прогнозной модели валютного курса.

Критерии, валютный курс, динамика, тренд, метод

Короткий адрес: https://sciup.org/140283467

IDR: 140283467

Текст научной статьи Эмпирическая идентификация типологических траекторий динамики временного ряда

Важной задачей статистического анализа является анализ тенденции динамики развития ВК инструмента. Прежде чем выявлять тенденцию, необходимо выполнить анализ случайности движения валютных курсов.

В неслучайных рядах (есть закономерность появления ряда данных), а ряд случаен, если он образован последовательностью независимых наблюдений [1, с. 499], существует некоторый тип зависимости между членами. Характеристикой этой зависимости является корреляция между последовательными наблюдениями. Проверка временного ряда на наличие тренда (идентификация текущего динамического поведения) может осуществляться разными методами [2]: метод средних, фазочастотный критерий знаков первой разности (Валлиса и Мура), критерий Кокса и Стюарта, критерий Аббе-Линника, критерии серий. Большинство критериев основаны на числе и структуре серий, обладают невысокой мощностью, например, критерий Вальда-Волфовитца и др.

Результаты и дискуссия

Рассмотрим критерий Аббе-Линника [3]: есть временной ряд (ВР) х ,,...., x_n взаимно независимых и нормально распределенных случайных величин с математическими ожиданиями ^ ,...., ^ , одинаковыми (но неизвестными) дисперсиями. Проверяем гипотезу принадлежности выборочных значений одной генеральной совокупности со средним µ –

H 0 : H i = _M , i = 1,2,...,

и альтернативу - тренд - H : | ^ .₊,— ^ .| > 0, i = 1,2,..., n - 1 .

n - 1

j E ( x + 1 ^- x ) ² Статистика критерия q = - - i =¹-------- , где

_ 1 n

X = -E x i . Если q > q a=0,95 , то n

² E ( X - x ) ² i = 1

нулевая гипотеза случайности ряда отклоняется с доверительной вероятностью a.

Критерий Кохрана [3, с. 517; 4] позволяет выявить скачок изменения среднего ВР после первых n i наблюдений ( n_i+n_i+1=n, i=2, „., n-1 ).

n ⁽ n ^— n ⁾⁽ x il ^— ^x _ip ) _ 1 ^_ 1

Статистика критерия: x 2 = ~---~----- ^p— , где xu =— E x ; x- =---- E x ;

n _x n i i = 1 ⁿ ^- ⁿii = n i + 1

X =1E Xi. Если x2 > X2(1), то изменение является значимым с n i=1

достоверностью a , x 2 (1) - a -квантиль распределения хи -квадрат с /=1 степенью свободы.

Хорошим критерием считается тот, который свободен от распределения, имеет минимум вычислений, должен иметь наибольшую мощность относительно альтернативы [1]. Таким является критерий поворотных точек. Поворотная точка (пик или яма) определяется как значение уровня, которое больше или меньше двух соседних.

Критерий поворотных точек: число поворотных точек равно kf = E x,, где X = 1 - поворотная точка, если ut < ui+, > uM или ut > ui+, < uM и x = 0 в противном случае, i=1,2,^,n-2, n - число наблюдений. Математическое

2( n — 2) ожидание числа поворотных точек для случайного ряда равно Mk = ——-

Дисперсия случайного ряда - Dk = 16n29. Сравнивая число поворотных точек исследуемого ряда k и случайного k , делается вывод о случайности ряда. Для этого проверяют нулевую гипотезу Ho: kf = ks - ряд случаен против альтернативной H : kf * ks - тренд. Сравнивая теоретическое значение tKp -критерия с распределением Стьюдента (с уровнем значимости α=0,05 и n-1 степенями свободы) и tф – фактическое значение критерия, делается вывод о случайности ряда: ks = Mk, стандартное отклонение случайного ряда

5 = D5k

k tф=-

—

—. Если г_ф > t_K , то нулевая гипотеза о случайности ряда

отклоняется [5] с доверительной вероятностью α .

Критерий инверсий. Пусть имеется выборка: х1, ….., хn. Инверсия имеет место быть, если хi > хj и (i+1) ≤ j ≤ n. Сумма всех инверсий в выборке I является статистикой критерия случайности выборки. При n ≥ 20 статистика I распределена приблизительно нормально со средним n (n — 1) 2 n3 + 3 n2 — 5 n I — M (I)

M(I) = -^-^ и дисперсией D(I) =----—----. При |I | = 1 ^^ 1 > ui+a гипотеза случайности отклоняется с вероятностью α. Точные критические значения I1(α), I2(α) можно посмотреть в специальной таблице. Если I1(α) < I < I2(α), то гипотеза случайности принимается. Считается, что критерий инверсий «хорош», «по эффективности он превосходит большинство непараметрических критериев тренда» [3, с. 535].

Непосредственное выделение тренда можно осуществить одним из трех методов: укрупнения интервалов [2, с. 128], скользящей средней и аналитического выравнивания. Недостатком скользящей средней является приближенность вычисления сглаженных начального и конечного уровней ВР. Метод аналитического выравнивания позволяет увидеть тенденцию развития ряда во времени как результат действия всех причинных факторов. Нас интересует направление и сила тренда (восходящий, нисходящий, боковой). Представление об этом дает коэффициент линейной регрессии по t цены закрытия.

Для предварительной идентификации исторического ряда, его участков восходящего, нисходящего и бокового тренда используем критерий поворотных точек, инверсий, критерий Кохрана и Аббе-Линника, а также графический анализ с помощью индикаторов и осцилляторов.

Структура исходной выборки имеет вид: это таблица, строки которой принадлежат определенной типологии динамики ВК (восходящий / нисходящий тренд), а столбцы - набор переменных (вектор X и их классификаций у ). Цель 1-го этапа методики - эмпирическое определение классификаций y . Для достижения этой цели автором предлагается метод эмпирической идентификации типологических траекторий динамики развития ВК. Процедура реализации метода состоит из трех этапов.

1. Проверка выполнения критериев:

- набор высоких максимумов и минимумов max t + 1 > max t ,

min t + 1 > min t (для V t ), на графике - восходящий тренд;

- набор низких максимумов и минимумов max t ₊ i < max t , min t ₊ i < min t (для V t ), на графике - нисходящий тренд;
- неравенства и < U i ₊ i > u i ₊ 2 или u i > и ₊ i < и ₊ 2 - выполнение
2. Подтверждение полученных промежуточных результатов классификации с помощью графического анализа значений некоторых индикаторов и осцилляторов в программе МетаТрейдер [6, 7] (рис. 1):

неравенств определяет точку разворота тренда.

- экспоненциальные средние (ЭС) ЕМА(5) , ЕМА(13) , ЕМА(21) помогают выявить направление тенденции, а их пересечение - разворот. Если быстрая ЭС выше медленной, то восходящий тренд увеличивает скорость, и наоборот, - нисходящий тренд увеличивает скорость;

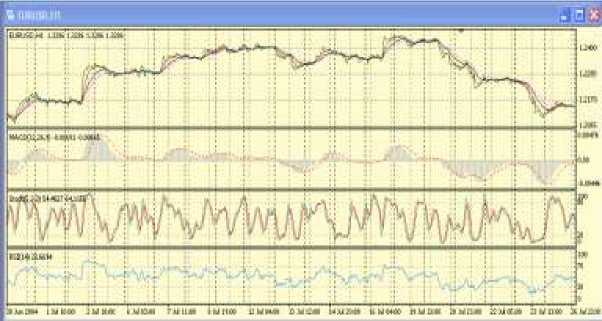
Рисунок 1 - Идентификация тренда по осцилляторам

- индикатор тенденции MACD повторяет тренд, пересечение оперативной и сигнальной линий показывает разворот, а расхождение направления движения цены и индикатора подтверждает этот сигнал;
- осциллятор RSI - пересечение уровней перекупленности или перепроданности показывает разворот, расхождение движения цены и осциллятора подтверждают разворот. По мнению некоторых авторов, нахождение осциллятора в зонах перекупленности или перепроданности сигнализирует о консолидации или развороте рынка [8];
- сигналы осциллятора Stochastic аналогичны сигналам осцилляторов, рассмотренным выше;
3. Анализ определения типологических траекторий ценовой кривой на основе применения критерия поворотных точек [1, с.486], инверсий (непараметрические) [1, с. 491] и параметрического критерия Аббе-Линника [47, с. 517] в предположении нормальности распределения валютного курса. Критерий Кохрана показал на всех интервалах тип поведения цены - флэт, то есть скачков не обнаружено, среднее интервалов исследования примерно одинаково.

Правила принятия решений таковы: при совпадении сигналов осцилляторов и выполнении (подтверждении) аналитических критериев, идентифицируется определенный тип тенденции: восходящий, нисходящий или боковой тренд, принимая во внимание, что «каждая тенденция завершается в торговом диапазоне, а флэт пробивается начавшимся трендом».

Теоретические значения статистик критериев для исследования данных взяты из соответствующих таблиц: непараметрический критерий инверсий - [3, с. 536, табл. 180]; критерий поворотных точек - [1, с. 486; 4, с. 130]; критерии Аббе-Линника [1, с.518, табл. 170] и Кохрана - квантили распределения хи -квадрат [3, табл.55, с.219].

Результаты эмпирической классификации динамических траекторий ВК с применением авторского метода представлены на рис. 2 и рис. 3. (часовые данные; 1 - нисходящий тренд, 2 - восходящий тренд, 3 - флэт). Исходные котировки валютного курса взяты для анализа с сайтов [9, 10].

АА

Дете U йремя 15 П5 2004 10 ПП 15 05 2004 11 00 16 Об 2004 12:00 16.06.2004 13.00 16.06.2004 14 00 16.06.2004 15:00 16.06.2004 16 00 16.06.2004 17:00 16.06.2004 10:00 И. mi. .1IM.I ....... 16.06.2004 20:00 1Б ОЬ 2004 21 ОО 1Б ОБ 2DD4 22 □□ 1Б ОБ 2DD4 23 ОО

17 05 2ОП4 П ПП 17.06.2004 1:00 17.06.2004 2:00

ГУЛ-Ц5

Тип-мах-

тип-цяна

нисхтренд

л о д^дф^лу нисхтренд нисхтренд

Д№- Пинмик-5

кр поло точек-

Крит поеор точек-30

ОНййрС ий

непере м =10

двее- Лин_0ин

«Р инеер_Зи H6U-10

xp_noeop _точ_3и Н6М-15

кр ПОЙ точек

Линем-10

точка разенисх тренднисх !рнндниик 1ренд точка разе нисх тренд нисх тренд нисх тренд

точка разе

нисх тренд нисх тренд нисх тренд нисх тренд нисх тренд нисх тренд нисх тренд нисх тренд нисх тренд нисх тренд нисм тренд нисх тренд нисм тренд

docx тренд

точка разе нисх тренд docx тренд

нисмтренд нисмтренд нисмтренд

точка разе веем тренд воск тренд нисм тренд

нисм тренд

точке разенисх тренднисх тренднисх тренд нисх тренд нисх тренд

ВОСХ тренд

17.06.2004 3:00 точка раза нисх тренд

нисх тренд

тренд

тренд тренд тренд тренд тренд тренд тренд тренд тренд тренд тренд тренд тренд

тренд тренд тренд флет флет

флет флет

тренд флет флет

17.06.2004 4.00

17.06.2004 5.00

17.06.2004 6:00

17.06.2004 7:00

17.06.2004 6:00

17.06.2004 9:00

1/ hi. .1IH.I I...... 17.06.2004 11 00 1/ ОЬ 2UU4 12 UU 17 ОБ 2004 13 □□ 17 ОБ 2ПП4 14 ПО

нисх |ренднисх тренд воск тренд

точка разе точка разе

воск тренд воск тренд воск тренд

воск тренд

тренд

нисх тренд

воск трвн^ воск тренд воск тренд воск тренд

воск тренд воск тренд воск тренд воск тренд воск тренд

dock тренд

docx тренд dock тренд точка разе воск тренд воск тренд

/ЛИСТ! 7

ЙОСИ ТрйНД

-ренд тренд тренд тренд тренд тренд тренд тренд тренд тренд

флы тренд тренд тренд тренд тренд тренд

тренд тренд тренд тренд тренд тренд

тренд

Рисунок 2 - Промежуточные результаты идентификации тренда (фрагмент)

	А	6	с	D	Е .		G	н	1	J	К	L М	N

1	Дата и время	Rt	V!	Ct		Rma<	юоэфф Ь за поел	прирост за 10 час %	MACDonep	RS^ МА%	чкчо	n«t#ew*oe тип omwcwew повод е за 10 час ения
2	17 06 04 1 00	0.СОО2	■ОД124	0,0002	0.0000	08002	88002	88424	08037	-20.2747	1.8240	0.000591 мио	1
3 »	17 06 04 2 00		ОД729	0,0000	0.0002	0,0006		-0,0025	0,0035	-2,9241	1.1926	0.000025 мисх	Г 1
Ь	17 06 04 4 00	0,0007	0.0818	0,0036	-0.0001	-0,0005	-0.СО01	-0,0033	0.0031	-20,5074	16.8644	0.000700 еос х	2
6	17 06 04 5 00	0.0006	4)2414	0,0005	0.0006	0,0008	0,0001	08025	0 8030	16.1922	29.3507	0,000568 «о»	2
7	17 06 04 6 00	0,0004	■02426	0.0005	0.0005	0,0003	0,0003	0.0092	00029	-13.3739	19.8506	0.000325 восх	2
	А	в	С 0		Е	F 1 6		н	I	3	к	L М	N
28	18 06 04 3 00	-0.0001	-0,5151	-0.0002	0,0001	0.0038	0,0005	-0,0150	0,0003	32,9219	6.9453	0.000066 мисх	1
29	18 06 04 4 00	-00016	0,3235	ДД017	4)0015	0,0034	8,0007	8,0474	0 0001	26.7415	7.4838	ОД01108 мисх	8
30	18 ОБ 04 5 ОО	■OJ0OO2	0,2728	-0.0003	-0,0010	-0,0012	-0,0009	-0,0499	-0Д001	23.6036	5 7788	0Д00249 мисх	8
31 32	18 C6J04 7 00	0ДО01	-0,0663	0.0002	4) 0007	•0,0014	-0,0010	ДД591	8,0003	-4 £896	о.оооо	0.000674 еосх	8 2
33	18 06 04 6 ОО	0 0012	0.4968	0.0012	0.0003	0,0018	8,0003	8,0457	8,0302	-11,1027	16.3710	0.001625 еосх	2
34	18 06 04 9 00	-0,0003	0,2213	4)0003	0,0002	0,0006	0,0000	-0,0424	0,0002	-25,5293	5.0623	0.000091 еосх	2
35	18 06 04 10 00	010016	41.1823	0JO016	0Д013	0,0016	0,0007	-0Д150	0,0000	-25,40-35	15.8444	0.001733 еосх	2
36	18 06 04 11 00	-0Д001	■0.3549	43.0002	00013	0,0000	0,0007	-08175	0,0001	30,3566	79775	0.000391 еосх	2
37	18 06 04 12 00	0JO015	0,2672	OJ0O14	0,0004	0,0017	0,0008	0,0058	0,0003	-41,9786	0.7518	ОД01439 еосх	2
зе	18 06 04 13 00	0.0018	0,1072	0JO0I9	0,0015	0,0019	0,0013	0,0249	0ДЮ6	■39.7822	52833	ОД01578 еосх	2
39	18 06 04 14 00	0.0025	0.4302	0.0024	0,0010	0,0024	0,0018	0,0656	0.0009	-41,9776	6.0618	0.001830 еосх	2
40	18 06 04 15 00	00021	-0,2470	ода?1	0,0831	0,0021	0,0024	0,0688	08012	-32 9150	3.8467	ОДО И 79 еосх	2
41	1806 04 16 ОО	0,0014	0,1513	0.0015	0,0024	0.D014	0,0024	0,1171	0,0015	-20,5364	2.9205	0.000233 еосх	2
42	18 06 04 17 00	-0.0004	■0,5603	■0 0036	0,0009	0.0001	0.0018	0,1121	0,0016	-16.3867	08155	ОДО 1533 еосх	2
43	18 06 04 18 00	0,0008	-0,4893	0Д009	0,0000	0,0002	0,0011	0,1087	одою	-9,2783	103319	0.000261 восх	2
44	18 06 04 19 00	00001	■1,2139	о дои	ОДООЗ	0,0006	0,0006	0,1128	00015	-4.9596	16.7731	0ДО1045 еосх	2
4-5	18 06 04 20 00	0,0006	-0,1147	0.0004	0,0009	0,0010	0,0004	0,1028	0,0014	-1,8302	11.0552	0.000450 восх	2
46	18 06 04 21 00	00002	■0,3962	0.0002	0,0003	0,0000	0,0005	0,1052	0.СО1Э	1,5078	92527	0Д0С687 еосх	2
47	18 06 04 22 00	-0.0001	0,9661	-0.0001	0.0002	0,0002	0,0003	0,0694	0,0011	6.0045	0.5397	0.000976 восх	2
48	21 06 04 000	4)0003	-0,5974	4)0008	41,0004	•0,0001	0,0001	0,0678	0,0009	158609	0.0004	ОД01О08 еосх	2
4 и	21 06 04 1 00	■0.0002	-0.1446	-0.0002	0.0000	-0,0006	-0,0002	0.0413	0,0007	29,8576	14.2683	0.000578 восх	2
50 51	21 06 04 2 00	goto	1,5616			0,0034	8,0003		0.СО05	21,9603	14.8148		2 2
52	21 06 04 4 00	-00013	■0,3462	Д.0012	4)0012	8,0010	8,0005	88074	0,0001	23,1340	18.6513	ОД01246 флет	3
53	21 06 04 5 ОО	0.0012	0.0669	0Д012	0.0000	0,0004	0,0003	-0.0041	0,0000	15,7673	17.9823	0.001197 флет	3
54	21 06 04 6 00	0,0007	•0,5839	ооооб	0,0012	0,0003	0,0000	0,0016	8,0001	9,6930	24.7916	0.00064 3 флет	3
55	21 06 04 7 00	00002	0,4394	одооз	-одазз	8,0002	0,0004	88025	•00001	10.3412	8,3361	0.0001 50 флет	э
56	21 06 04 8 00	-о.ооов	1,0485	43.0037	-ОДОЮ	0,1X02	0,0004	-08’24	♦0,0002	15,7484	21,9436	ОДОО701 флет	3
57	21 06 04 9 00	-0JO025	-0,0610	-0.0025	-ОДОМ	8,0008	8,0007	■0,0363	8.0304	816561	39.3409	0.062115 флет	3
58	21 06 04 10 ОО	0,0003	-0,3660	0.0002	-0,0004	■0,0017	-0,0011	-0,0297	-0,0006	4.0305	0.5335	0.000628 флет	3
59	21 06 04 11 ОО	0,0000	0,0545	0.0000	4)fl00>	8,0001	8,0010	80281	80006	6.3788	5.5251	0,000281 флет	3
60	21 06 04 12 00	-0,0007	0,1574	-0,0006	-0,0005	0,0002	0,0006	-0Д322	-0,0007	-14,2152	10.6627	0.000339 флет	3
	"Ч« /V П» 11,рп Opr>Yi А «ПГТ А А ПА-1« Г>₁АЛАА А АА« е ► *i X Гкст1 Z Г¥ст7 /ГМст2 / Листб / ПмсТ5 /Г¥<т4 V ЛчлЗ /						\|”"W>		--»	* /VWS	””4		7

Рисунок 3 – Результаты эмпирической идентификации тренда (фрагмент)

Выводы

Предложенный метод эмпирической идентификации типологических траекторий динамики валютного курса позволил с достаточной степенью близости определить тип динамического поведения ВК на контрольных данных, сопоставимого с результатами проверки с помощью известных трендовых осцилляторов.

Полученные результаты в дальнейшем могут быть использованы для построения модели прогнозирования динамики валютного курса финансового инструмента и построения эффективных инвестиционных стратегий на основе алгоритмической торговли.

Список литературы Эмпирическая идентификация типологических траекторий динамики временного ряда

Кендалл, М. Дж. Многомерный статистический анализ и временные ряды/ М. Дж. Кендалл, А. Стьюарт. - М.: Наука, Главная редакция физ.-мат. литературы, 1976. - 736 с.
Статистика: Учебное пособие/ Харченко Л.П., Долженкова В.Г., Ионин В.Г. и др.; Под ред. В.Г. Ионина. - Изд. 2-е, перароб. и доп. - М.: ИНФРА-М, 2005. - 384 с.
Кобзарь, А.И. Прикладная математическая статистика. Для инженеров и научных работников/ А.И. Кобзарь. - М.: ФИЗМАТЛИТ, 2006. - 816 с.
Закс, Л. Статистическое оценивание/ Л. Закс: Пер. с нем. В.Н. Варыгина. Под ред. Ю.П. Адлера и др. - М.: Статистика, 1976. - 598 с.
Статистика финансов: Учебник / Под ред. В.Н. Салина. - М.: Финансы и статистика, 2000. - 816 с.
Торговля на Forex с брокером №1 в Москве и России [Электронный ресурс]. - Режим доступа: www.alpari.com (дата обращения: 05.06.2018).
Крюков, П.А. Методические основы типологической классификации динамики валютного курса/П.А. Крюков// Банковское дело. 2011. №6. С. 81-85.
Якимкин, В.Н. Как начать зарабатывать на валютном рынке Forex/ В.Н. Якимкин. - М.: СмартБук, 2008. - 352 с.
Архив котировок [Электронный ресурс]. - Режим доступа: https://www.teletrade-dj.com/ (дата обращения: 05.06.2018).
Котировки EUR/USD [Электронный ресурс]. - Режим доступа: https://www.finam.ru/profile/forex/eur-usd/export (дата обращения: 05.06.2018).

Еще

Статья научная