Эмпирическая модель теплового состояния роторных подшипников и масляной системы ГТД

Однако температурные параметры масло-системы и подшипников, прежде всего, зависят от режима и условий работы ГТД. Таким образом, сам факт изменения температур масла, подшипников еще не говорит об изменении технического состояния. В качестве примера на рис. 5 приведен график изменения входной температуры масла за время полета (для одного из двигателей «НК»). Видно существенное изменение температуры масла, обращает на себя внимание также длительный участок «прогрева» масляной системы до относительно установившихся значений. Существенно изменяется температура масла на входе и для индустриальных двигателей. Аналогично изменяются и температуры подшипников.

Традиционные методы допускового и трендового анализа параметров не позволяют в полной мере учитывать влияние режимных параметров и внешних условий. Для надежного выявления неисправностей и возможного исключения ложных срабатываний необходимо применение модели, позволяющей учитывать влияние режима и условий работы двигателя. Существующие расчетные методики определения теплового состояния маслосистемы и подшипников (например, представленные в [3]), как правило, являются достаточно сложными и одновременно весьма приближенными, так как не позволяют учесть многие индивидуальные особенности конкретного типа и экземпляра двигателя. Подобные методики используются при проектировании, однако для решения задач диагностирования, когда двигатель уже разработан и эксплуатируется (или испытывается) рационально применить другой подход, основывающийся на использовании полученных экспериментальных данных.

о а ® m ю: ж ia ю ж» ж га га х» яс я» га га ах га

№2«1Ш2                                    ^„«у                                    №i®2te?21

Рис. 2. Разрушение радиально-упорного подшипника. Изменение параметров (температуры масла на выходе из двигателя и температуры подшипника) при аварии

Рис. 3. Пример состояния суфлера масляной системы после аварии

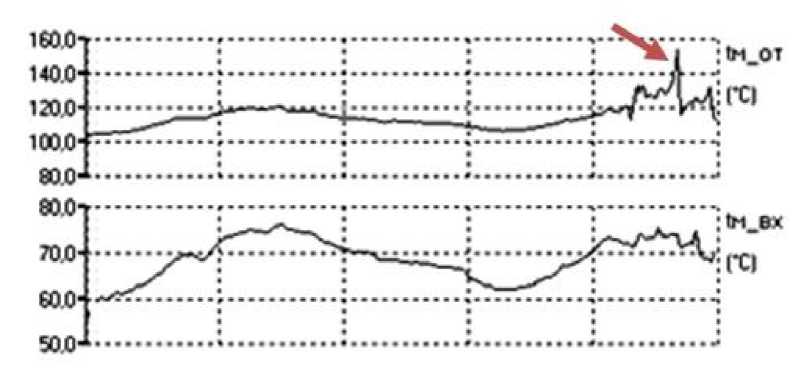
Рис. 4. Разрушение суфлера масляной системы. Изменение параметров (температур масла на входе в двигатель и выходе из опоры турбины) при аварии

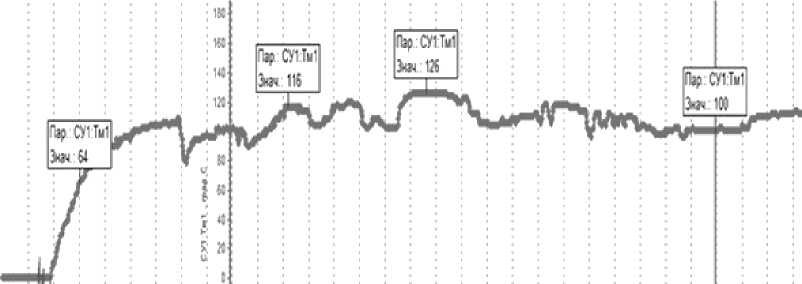
Рис. 5. Пример изменения температуры масла за время полета

Для определения взаимосвязи какого-либо параметра и влияющих на него факторов предлагается использовать метод регрессионного анализа, реализуемый, в частности, в программе Statistica. В данной программе задавался вид формулы (модели), связывающей исследуемый параметр с режимными факторами и внешними условиями, а неизвестные коэффициенты подбирались программой, решающей итерационным численным методом задачу наименьших квадратов (методом Гаусса-Ньютона или Левен-берга-Маквардта). Для выполнения расчета задавалась выборка измеренных значений параметров работы двигателя при проведении стендовых испытаний, или выборка данных, полученная в эксплуатирующей организации (отражающая работу двигателя на разных режимах и в различных условиях).

Принятый подход в определенной степени перекликается с нейросетевым методом [4]. Так же, как и при нейросетевом подходе к диагностированию, задается «обучающая выборка», позволяющая идентифицировать модель. Однако, в отличие от нейросетевого подхода, сам вид связи исследуемого параметра и влияющих факторов задается предварительно в виде формулы, полученной на основе как исследования физической взаимосвязи параметров [2], так и с учетом имеющегося опыта диагностирования и тепловых расчетов, в то время как в нейросети эта связь представляет собой «черный ящик» и определяется структурой сети и автоматически подбираемыми значениями весовых коэффициентов. Таким образом, применяемый подход позволяет более наглядно понимать взаимосвязь исследуемого параметра и влияющих на него факторов.

Вид формулы (модели), описывающей взаимосвязь исследуемого параметра и влияющих на него факторов:

- для температуры подшипника (более подробно рассмотрено в [2]):

где:t п – расчетная температура подшипника; n отн_р – физическая частота вращения ротора двигателя, отнесенная к некоторому выбранному характерному режиму работы (например, максимальному продолжительному); t мвх_отн_р – температура масла на входе, отнесенная к температуре на некотором выбранном характерном режиме работы; G м_отн – относительная прокачка масла через двигатель, которая определяется следующим образом:

G M _ отн = ^0,412 • 4(РмвХ ^— Рс^уфл)

где Р мвх – давление масла на входе в двигатель; Р суфл – давление в системе суфлирования; A, b, c, d – эмпирически получаемые коэффициенты.

- для анализа теплового состояния масляной системы предлагается использовать величину «подогрева» масла, т.е. разницу выходной и входной температуры масла. Величина подогрева масла в двигателе может быть описана зависимостью:

Δ t м = d · t м.вх отн р ^a · t вх пр · Р к отн ^c ,

tп

a

= n       • t отн _ р   мвх отн _ р

b • G м отн

d

• с

где: Δt м =t м_вых_дв – t м_вх ; Р к отн – давление за компрессором двигателя, отнесенное к некоторому выбранному характерному режиму работы (например, максимальному продолжительному); t мвх_отн_р – температура масла на входе, отнесенная к температуре на некотором выбранном характерном режиме работы; t вх пр =( t вх +273)/288; A, b, c, d – эмпирически получаемые коэффициенты.

Кроме величины подогрева масла в двигателе в целом, отдельно можно рассмотреть подогрев масла в опоре турбины (Δt м от =t м_вых_от – t м_вх ), в связи с измерением на двигателях «НК» температуры масла на выходе из нее. Формула для расчетного определения указанной величины аналогична формуле (2), отличаются только значения коэффициентов a, b, c, d. Для одного из трехвальных двигателей «НК» получены следующие значения коэффициентов уравнения (1) для расчета температуры радиально-упорных подшипников (температура которых измеряется в эксплуатации), представленные в табл. 1.

,   (1)

Таблица 1. Значения коэффициентов модели температурного состояния радиально-упорных подшипников

Коэффициент	Подшипник ротора НД	Подшипник ротора СД	Подшипник ротора ВД
а	0,157	0,555	1,295
с	70	93	122,6
в	1,232	0,862	0,591
d	-0,07	-0,01	-0,45

На рис. 6 представлен пример результатов сравнения расчетного и фактически измеренного значения температуры подшипника

ротора НД за время проведения стендового испытания. Видно хорошее совпадение результатов расчета и эксперимента, начиная от запуска и до

момента останова двигателя. Полученные результаты вполне позволяют подобную модель применять для диагностирования двигателя, для расчета «эталонной» температуры подшипников (в предположении исправного состояния двигателя) с учетом фактического режима и условий работы.

Для формулы (2) расчета величины подогрева масла в двигателе получены следующие значения показателей степеней: с=1,16; a=4,107; b=0,295; d=1,426. На рис. 7 представлено сравнение величины расчетного и измеренного подогрева масла за время испытания двигателя. Также, как и для температур подшипников, получено хорошее совпадение результатов расчета и эксперимента, позволяющее решать задачи диагностирования.

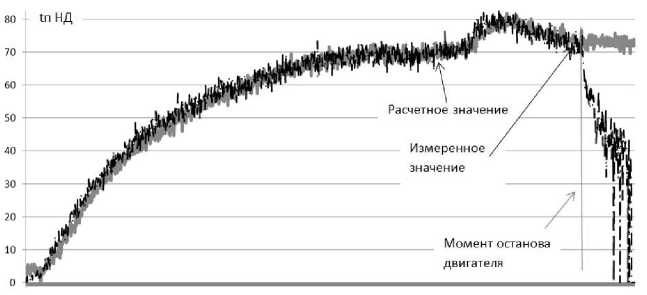
Рис. 6. Сравнение измеренной и расчетной температуры подшипника НД

Дем дв

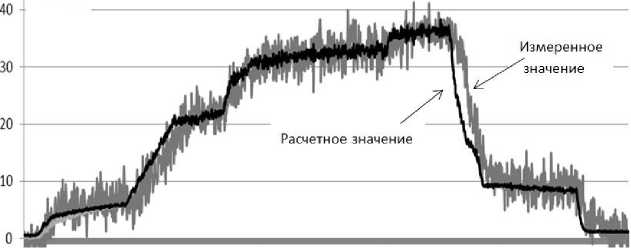
Рис. 7. Сравнение измеренного и расчетного подогрева масла в двигателе

Предлагается следующее использование представленных моделей для диагностирования двигателя:

• 1)    допусковый контроль отклонения измеренного и расчетного значения (позволяет выявлять «развитые» неисправности);

• 2)    трендовый (с использованием критерия Аббе) анализ тенденции поведения разницы расчетно-

• го и измеренного значения температуры за определенный период наработки (позволяет выявлять неисправности в начальной стадии развития).

Значение критерия Аббе рассчитывается по формуле:

n

г = 1 £( П -П,-1)2 е (п - п )2

i = 1        *        ср

где: П – значение параметра, по которому проводится трендовый анализ; П ср – среднее арифметическое значение параметра за определенный период времени. Если полученное значение r<0,5482, делается вывод о наличие тренда.

На рис. 8 приведен пример использования температурной модели для случая реального изменения параметров при разрушении подшипника (имеющиеся отличия в значении расчетной и измеренной температуры в данном случае объясняются тем, что, в отличие от формулы (1), не был произведен учет прокачки масла в связи с отсутствием необходимых данных по изменению давления масла и давления в системе суфлирования). График построен по данным работы двигателя за последние пять суток перед аварией.

Применение модели позволяет обнаружить анормальное поведение параметра (в данном случае температуры подшипника) значительно раньше, чем будет достигнуто его предельно-допустимое значение (для температуры подшипника - 200°С, на рис. 7 температура еще не достигла предельно-допустимого значения), и принять решение по дальнейшей эксплуатации. Сказанное так же относится и для использования модели расчета подогревов масла. Таким образом, достигается более раннее выявление развивающихся неисправностей.

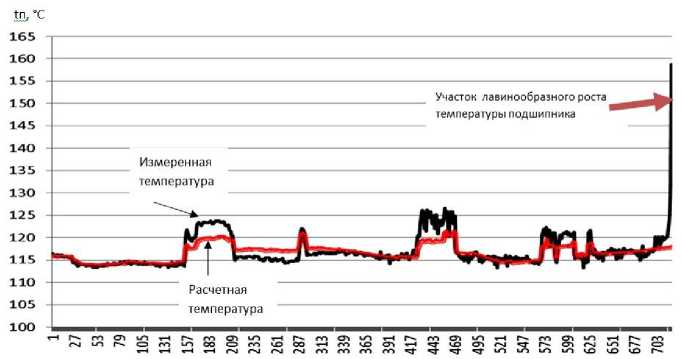
Рис. 8. Сравнение величин расчетной (по модели) и измеренной температуры подшипника в ходе аварии (разрушение радиально-упорного подшипника ротора ВД)