Эмпирическая оценка длительностей циклов по их амплитудным характеристикам

В задачах прогнозирования солнечных циклов или их реконструкции в прошлом, кроме вычисления максимального значения цикла Wm, важна и оценка его длительности Тс. В работе предложено несколько подходов, связывающих Тс с характеристиками цикла. Рассматриваются циклы достоверного ряда чисел Вольфа (циклы 10–22). При расчетах использована идея Вальдмайера рассматривать Wm как независимую переменную. Экспериментальные кривые аппрокси-N мируются разложениями типа ∑ akWmk . Соответствующие коэффициенты разложения приведены в таблице. При по-k=0

стулировании или использовании эмпирической связи площади цикла с его длительностью получены простые зависи мости Т _с от W _m и дана оценка длительности 23 цикла . Показано , что , кроме относительных погрешностей , для оценок Т _с разумно сравнивать и суммарную длительность циклов . Полученные критерии для циклов 10–22 применены при оценке восстановленных циклов 1–9, при этом отмечены существенные отличия .

Estimation of a cycle duration Тс, along with calculation of the cycle maximum value Wm, is of importance to prediction problems of solar cycles or their reconstruction in the past. Several approaches connecting Тс with cycle characteristics are presented in the paper. Cycles of reliable Wolf-number sequence (cycles 10–22) are examined. The Waldmeier idea of regarding Wm N as an independent variable is used in calculations. Experimental curves are approximated by expansions of ∑ akWmk type. Cor-k=0

responding expansion coefficients are shown in the table. Simple Т _с dependences on W _m are derived, and estimation of the duration of the 23^rd cycle is given due to postulation and application of empirical relations between the cycle area and duration. The paper proves that the total duration of cycles, along with relative errors, should be compared to estimate Т _с . The criteria obtained for cycles 10–22 are used for the estimation of reconstructed cycles 1–9; the estimation allowed establishing of significant differences.

Наиболее простую оценку длительности цикла Т _с можно получить, исходя из площади цикла S _c и площади треугольника Т с = 2 S c / W m . Для сглаженных за 13 месяцев чисел Вольфа W * эмпирическая зависимость S c от W m и ее аппроксимация представлены на рис. 1 (слева). Используя эту зависимость, S c ( W m ), можно оценить длительности цикла по заданному W m . На рис. 1 (справа) для циклов 10–22 приведены относительные погрешности ( T – T _c)/ T оценки Т _с в сравнении с табличной длительностью T . Сравнение дано для трех представлений чисел Вольфа: W *, Р 14 и Р 13, отображенных соответственно крестиками, кружками и квадратами. Ряды Р 14, Р 13 рассмотрены в [1]. Представление Р 13 получено из ежемесячных чисел Вольфа с удалением временных периодов, меньших 4.26 года. В представление Р 14 включены квазидвухлетки, т. е. удалены периоды меньше 1.5 лет. Суммарная табличная длительность рассматриваемых 13 циклов составляет 1686 мес., а для рядов W *, Р 14, Р 13 соответственно 1601, 1587, 1634 мес. В целом можно отметить заниженную оценку длительностей циклов и накопление ошибки при их объединении.

Следует ожидать улучшения оценок при исполь- зовании двух экспериментальных параметров. Поскольку ветви роста и спада отражают различные процессы, разумно дополнительно использовать такие характеристики ветви роста, как ее длительность Tm и площадь 5m. Используя углы P и Pm (рис. 2, справа) как переменные, имеем Тс=2WmsinP/(cosP+cos(P - 2Pm)). На рис. 3 (слева) представлены P, Pm и их аппроксимация от Wm для ряда W*. Сравнительный анализ относительных погрешностей для рядов в представлениях W*, Р14 и Р13 приведен на рис. 3 (справа). Суммарные длительности циклов в месяцах для рассматриваемых рядов равны соответственно 1681, 1679, 1682 и близки 1686. Видим, что при использовании предложенных

Рис . 2.

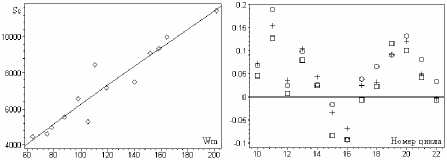
Рис . 1.

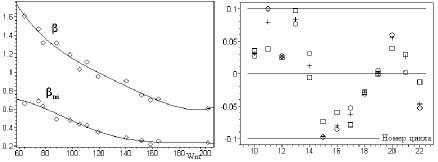
Рис . 3.

Эмпирическая оценка длительностей циклов по их амплитудным характеристикам аппроксимаций разброс относительных отклонений ≤ 10 %. У цикла 23 (W*)m = 120.8, и оценка его длительности дает 133 мес. Для представлений Р14 и Р13 соответственно получаем 131 и 135 мес.

В рамках изложенного подхода и полученных выше критериев рассмотрим циклы 1–9 с суммарной табличной длительностью в 1209 мес. На рис. 3 (слева) приведены относительные погрешности этой оценки. Строго в 10%-й интервал попало три цикла и два близки к нему. Циклы 2, 4–6 существенно отклонились. Оценка суммарной длительности дает 1282 мес. и весьма отличается от табличной. Столь значительные отклонения можносвя-зать с существенными искажениями значений чисел Вольфа при их реконструкции. В [2] использовано правило Вальдмайера, связывающее убывание длительности ветви роста цикла с возрастанием его максимума Wm. На основе интерполяции этой эмпирической зависимости анализируется гипотеза о «потерянном» цикле в конце XVIII века, но достоверность самого минимума Дальтона не оценивается.

Коэффициенты аппроксимации функций Sc, β, βm для чисел Вольфа W*