Энергетическая модель литий-ионной аккумуляторной батареи

Operating with enormous energy flows, modern technique requires autonomy systems of energy storage. This often makes the storage batteries indispensable in an autonomous and stationary power industry.

The specialty of storage batteries is that, on the one hand, the processes occurring in the storage batteries are subjected and described by the laws of chemistry and electrochemistry, and on the other hand, external behavior of the storage battery as the element of an electric circuit are subjected and described by the laws of physics and electrotechnic. The processes within the storage battery are nonlinear, and the processes occurring outside of it, can be linearized and subjected by known Ohm’s laws.

This is the main reason for the absence of general mathematic description of the storage battery as an electrical device. Overwhelming majority of papers studies devoted to storage batteries is dedicated to research of the processes on the surface and inside the electrode, the electrolyte and other parts of the storage battery and the interpretation of its external behavior, i.e. measurement and calculation of voltage and electric current [1].

Problem statement

The first attempts to represent discharging curves were made in 1897 by M. Peykert and consisted of the establishment of a functional connection between the amperage and the discharge time as a hyperbolic dependence Iⁿ ∙ t = C ; where I – discharge current, t – discharge time, C – independent on the capacity and characterizing the giving type of the storage battery; n – constant related to the weight of active material.

The expansion of the applications of the storage batteries (e.g. in autonomous systems of power supply for vehicles and power electronic equipment) has resulted in necessity of describing a family of discharge characteristics as follows: charge/discharge voltage – is a function of charge/discharge current, temperature and current capacity [2].

When designing the autonomous systems of power supply it is necessary to have energetic models of separate elements of such systems in order to determine parameters of these elements. The best way is to use computing simulation. We have attempted to create a model of system of power supply in MatLAB 7.9 (Simulink). The existing model of storage battery in MatLAB has significant disadvantages because ignores:

• -    The effect of temperature on the output voltage

• -    Self-discharge of the storage battery

• -    Degrading changes of the storage battery, associated to time

• -    Heat release of the storage battery.

Accordingly, the task is to modify the specified model and test it to determine the efficiency.

Problem solution

To solve this problem we use visual modeling medium Simulink, which is part of the package MATLAB 7.9. One of its main advantages is the ability to model, combining the methods of structural modeling and simulation. This approach, in contrast to circuit simulation package, allows to significantly simplify the model, and increase the speed of computation.

The model of the storage battery

Fig. 1 shows a model of a lithium-ion battery, created in Simulink. User can change parameters such as the maximum capacity of the storage battery, rated operating voltage and ambient temperature [3, 4].

Fig. 2 shows the hierarchical structure of the block «Lithium-ion battery». Changes made to the model are marked red. Blocks «From9» and f(u)1 are responsible for the dependence of the output voltage of the external temperature; blocks From10, From11 and f(u)2 are responsible for the dependence of the capacity of the external temperature and the time; blocks I_SR and I_R take into account the self-discharge of the storage battery; block T calculates the temperature of the storage battery.

Figure 3 shows the expressions that are defined according to U=f(T) и C=f(T, time). Dependencies were obtained by approximation of experimental discharge curves shown in Fig. 4

The model testing

Fig. 5 shows the discharge characteristics of the storage battery, taken off at a nominal temperature of 20 ° C and a discharge current of 1 A.

Fig. 6 shows the model consisting of 9 storage batteries, Fig. 7 shows its discharge characteristics.

Fig. 8 shows the discharge characteristics, taken from 9 storage battery at different temperatures (Fig. 8a) and currents (Fig. 8b).

As can be seen from the graphs, the temperature decreases, decreasing the maximum voltage and battery capacity, while increasing the discharge current AB depletes the battery quickly, and the maximum voltage does not change.

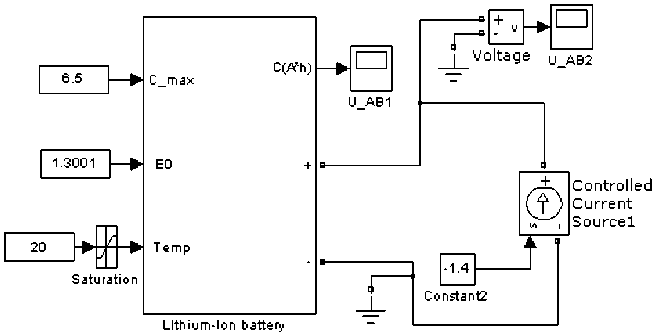
Fig. 1. The model of the lithium-ion storage battery

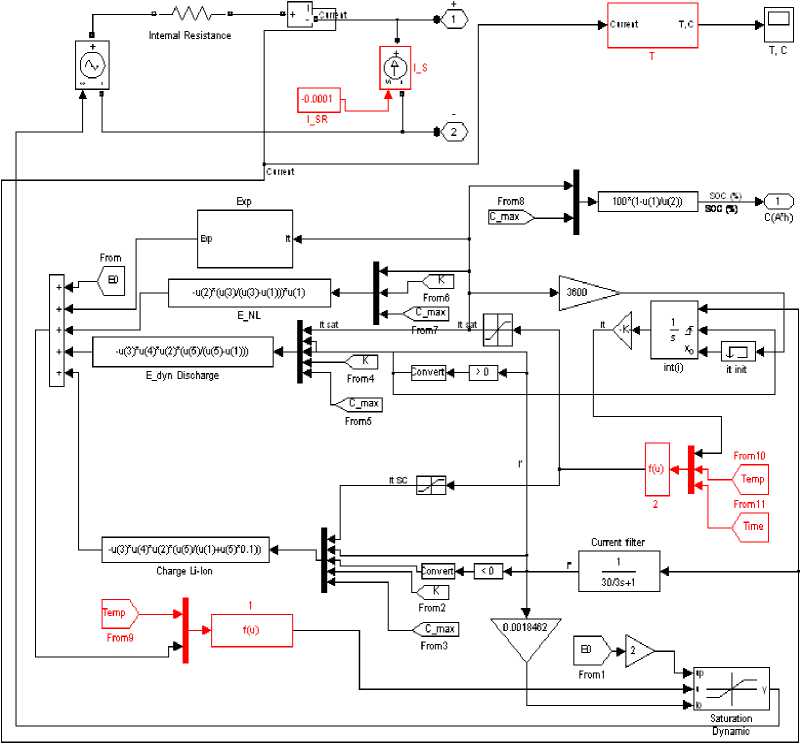
Fig. 2. The structure of the hierarchical block Lithium-Ion battery

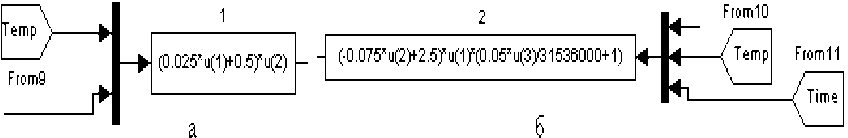
Fig. 3. Expressions that specify dependences of output voltage and capacity as a dependence on the temperature and time: a - dependence U=f(T); b - dependence C=f(T, time)

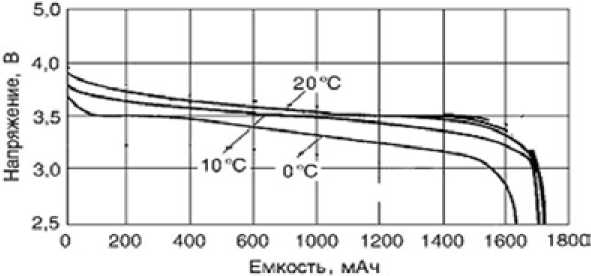
Fig. 4. Discharge characteristics of the lithium-ion storage battery, taken at different temperatures

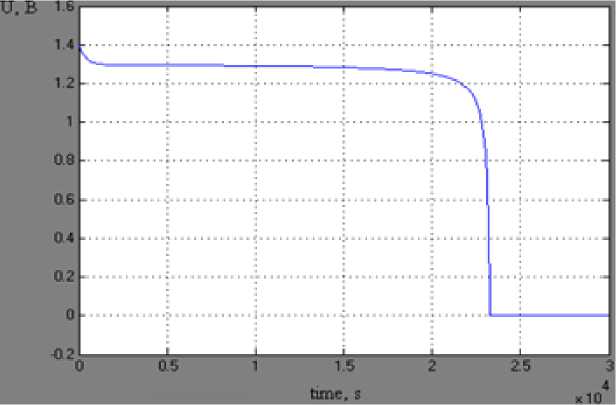
Fig. 5. Discharge characteristic of the lithium-ion storage battery

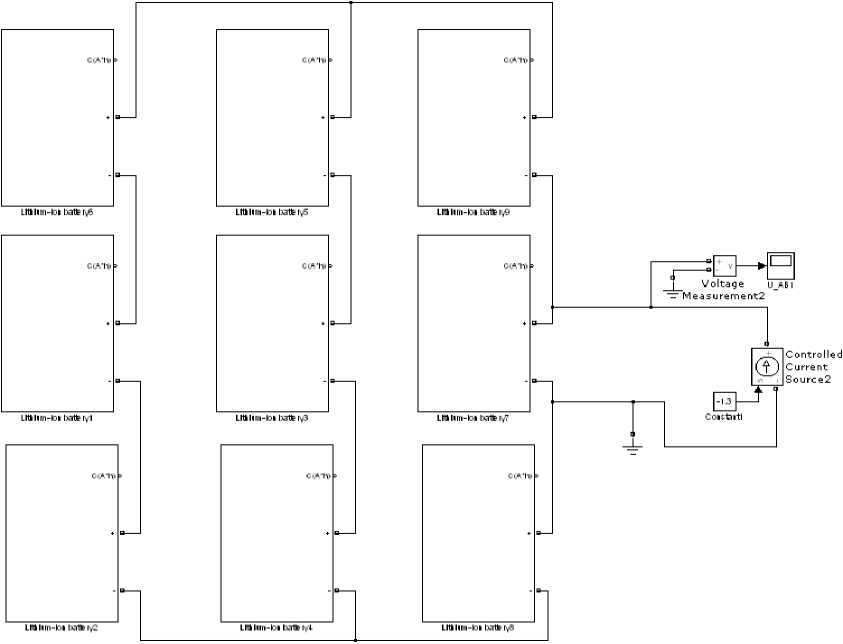
Fig. 6. The model consisting of 9 storage batteries

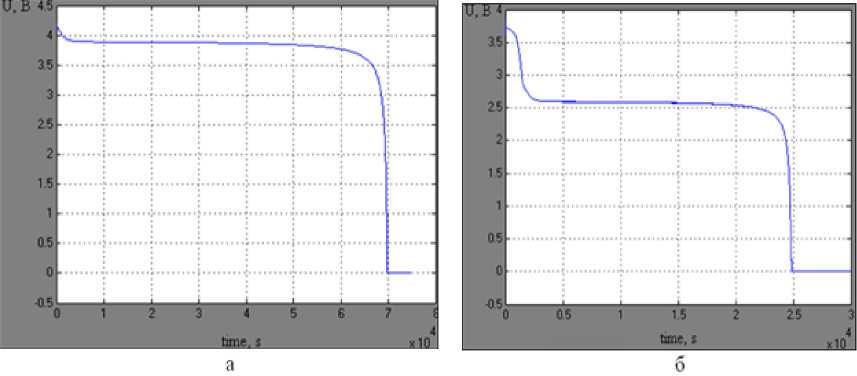
Fig. 7. Discharge characteristics of the model consisting of 9 storage batteries: a – discharge characteristic taken off 9 storage batteries; b – discharge characteristic taken off 9 storage batteries one of which is out of order

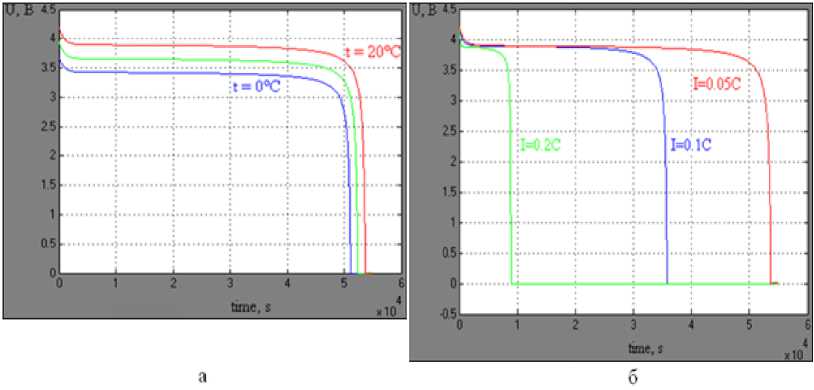
Fig. 8. Discharge characteristics of the nine AB, taken under different external actions: a – characteristics, taken at different temperatures; б – characteristics, taken at different discharge currents

Conclusion

There is a model of the storage battery, which takes into account changes in temperature, heat dissipation, self-discharge and degrading changes. Characteristics obtained during the test battery confirm its performance, the model can be used in the design of various power systems.