Энергетическая модель механики в горном деле

z                                          i

Скалярные коэффициенты ki должны характеризовать либо физические свойства материала, например плотность материала при вычислении кинетической энергии частицы, либо свойства среды, в которой происходит движение, например ускорение свободного падения при движении в гравитационном поле Земли. Гипотеза (9) может быть расширена, например, за счет учета взаимных влияний инвариантов, т. е.

добавлением слагаемых, определяемых значениями двух и более инвариантов.

Дальнейший анализ ограничим формулировкой обобщенного закона движения механической системы в виде закона сохранения энергии на бесконечно малом интервале времени d Ж = O', (d^ ki^i) - ddEe = 0.                       (10)

i где Ес - энергия внешних воздействий. Оператор «d» - соответствует бесконечно малым приращениям функции во времени в отличие от оператора « 5 », используемого для бесконечно малых приращений функций в пространстве переменных Лагранжа.

Уравнение (10) предполагает определение бесконечно малых приращений энергии, которые могут быть вычислены на приращениях, выбранных для описания движения кинематических координат qj, используемых в правых частях уравнений перечисленных выше инвариантов dSEt(k^i(qj)) = Vokt ^d dqj = Qjddqj.(11)

q j

Множитель Qij по существу является энергетическим определением обобщенной локальной силы

Q  55E = k <^50 ,(11а)

11                               i0

qj         qj характеризующей скорость изменения соответствующего вида энергии Ei бесконечно малой частицы при изменении кинематического параметра qj. В общем случае сила Qj может быть скаляром, если в качестве кинематического параметра выбран скаляр, например путь s или квадрат скорости v2, вектором, если параметры qj являются проекциями вектора, или тензором 2 ранга. Размерность силы Qij также зависит от выбора кинематической координаты qj, например [Н] или [Нм] для линейных или угловых перемещений, [Па] для тензора напряжений Лагранжа и пр.

Закон сохранения энергии (10) предполагает учет всех как внутренних, так и внешних энергетических факторов. Для учета энергетических потоков со стороны окружающих частиц воспользуемся общепринятой методикой, использующей скалярное произведение векторов силы РР и скорости v : dЕе = ^(<5P -v)dt. Суммирование в правой части должно быть проведено по всем ограничивающим рассматриваемую бесконечно малую частицу поверхностям. С учетом возможных изменений сил и скоростей на противоположных гранях, предполагая все функции дифференцируемыми и заданными в переменных Лагранжа, получим с точностью до бесконечно малых 1-го порядка (по пространственным переменным и времени), dЕ

о ⁼ zz— ⁼ x„i^xi _tn⁺ X _t5^nt / da„

Vdtt     pi i’tp     i’t pi      p где Tpi = (8Pp/дар)Vo - напряжения Лагранжа, образуют несимметричный тензор второго ранга. Индекс p е (ос, р,у^ указывает направление нормали к рассматриваемой площадке в исходном состоянии, а индекс i - направление проекции силы, может принимать значения i е(х, y, z) . Напряжения т. подобны напряжениям Пиола - Кирхгофа [6], но отличаются от них ограничением области изменения аргументов и неоднозначным выбором начала отсчета шкалы средних напряжений, которое может быть смещено относительно общепринятой [3-5].

С учетом внешних взаимодействий закон сохранения (10) можно записать в форме энергетического баланса dЕ=Vkk£,t +k2^,t +k^3,t +-+^At -^)dt -0.        (10а)

Пренебрегая процессами диссипации (т. е. без учета инвариантов, связанных с интегрированием по времени), а также используя общепринятые соотношения для потенциальной и кинетической энергии (ось z направлена вертикально вверх)

dЕ\ = РоgztdVodt,         dЕ2 = Po (xtxtt + У .У « + ztztt)dVodt, получим d Ex + d SE2 + d Es + d 8E6 + d Еп = об Vodt, или, с учетом дифференциальных уравнений движения, Г pixi, tp = k5( xta^ytp^ztr ) +

⁺ 2 k^ ⁽ x_ax_ta + xpxp + x₇x_t7 + y_ay_ta + y_py _tp + y₇y _ty + Z_aZ _ta + ZpZ _tp + Z_yZ _ty ) ⁺

^{+ k}7⁽~a^Xta ^XXp^Xt_P^Xx₇^Xty ^yy_ay_ta ^УУрУхР yy₇y_t7 z^a^ta ^У-р-_1Р z^Z₇²t _Z) •        ⁽¹⁴⁾

Приравнивая коэффициенты при одинаковых множителях - компонентах тензора скорости деформации (7), получаем соотношения между компонентами напряжений, элементами тензора (3) и константами ki, характеризующими физические свойства материала, тpi =к5 dpt +2 k6 xi, р +kД, р •                              (16)

В соотношениях (16) и далее Х_Рр - алгебраические дополнения элементов x_ip матрицы (3), единичный тензор 5_pi принимает значения 5_ni = 1 при соответствии индексов « р » и « i », т. е. 6. = 1 для г,^,^ и pi                                                                                                 pi                  х     у z

8pi = 0 для всех остальных напряжений, не расположенных на главной диагонали. В исходном состоянии, когда переменные Эйлера и Лагранжа совпадают (матрица якобиана преобразуется в единичную), компоненты тензора определяют только физические свойства т =то. =т =k,-v'lk,-vkn , Тп.=т =т =т =т =тп =0.

X ООС У ру     z yz      5        6      7 ,             X рх     X XC     у оу     У уу я О(Я я ря

Энергетический баланс должен выполняться в любой, в том числе начальный, момент времени, для которого можно использовать напряжения Коши ам dЕе / V^dt^axti ti. е                    j J,ti

Переходя в уравнении (17) от производных по переменным Эйлера Xx^J Хх^х1>ц к производным по переменным Лагранжа x^ /дap=xUp с помощью общих соотношений, вытекающих из уравнений движения (2) f / Хх. =(df /да^ХуpR R , и приравнивая коэффициенты при одинаковых множителях x в правых частях уравнений (12a) и (17), получим систему линейных уравнений тр t=аj -~j, р , (18а) которые формально совпадают с известными статическими условиями на контуре и по существу определяют связи между напряжениями Лагранжа и Коши, справедливые для любого момента времени

°"л=^трХ , р ^{1 R} . ^(18b)

Равенства (18b) можно трактовать как следствие условия инвариантности энергии по отношению к выбору начала отсчета времени в системе наблюдателя. С учетом (16) для напряжений окончательно получаем о . = — I           „ + т х- = — ^«х. + 2кАх х +     „ + х- х ) + кАх х + х • „х- „ + х. ~ ) , ji j^   ca-^j ,а 1 ipf^j ,Р i}t^J — j^   i5  j,«    ^,V6V ^-,a "^j ,a  1       ^j    1 ^i,/^j ,y7 1 ,v7 V ^j ,a ^i ,a  1 ^j ,g   ,g 1 ^j ,y *^i,//   ’

(18с)

Сопоставление выражений (16) и (18с) показывает, что для анализа процессов деформации грунтов напряжения Лагранжа предпочтительнее: они энергетически обоснованы и связаны простыми математическими уравнениями с имеющими четкий геометрический смысл характеристиками деформированного состояния. Основной инвариантной характеристикой напряженного состояния можно считать среднее напряжение Коши

3 aR = k₅^_s+2k 6^6 +3 k 7^7 ,                            (19)

которое можно использовать для определения среднего напряжения в исходном состоянии olt=0= k5+2k6 +k7 .                                (20)

Если коэффициенты k5 - k7 , характеризующие физические свойства деформируемого материала, известны, тогда по уравнениям движения в форме (2) можно определить любые кинематические, а затем и энергетические или силовые функции, в том числе напряжения Лагранжа (14) и Коши (18). Они могут быть использованы для корректировки (выбора) начала отсчета шкалы средних напряжений. Есть достаточно оснований считать, что в исходном состоянии средние напряжения не следует принимать равными 0. В частности, закон упругого изменения объема в механике деформируемого твердого тела о = 3 Ке можно считать совпадающим с законом изотермического расширения газа pV const , если модуль объемной упругости К рассматривать как действующее в текущем состоянии давление.

Из закона сохранения энергии в форме (10) следует, что деформация возможна при изменении не менее двух видов энергии (или работы внешних сил). Это позволяет установить связь между коэффициентами ki и привести систему отсчета различных видов энергии к одной шкале.

В качестве примера рассмотрим зависимость между коэффициентами k1 и k2 на примере свободного падения абсолютно твердого тела (частицы) в гравитационном поле Земли, в котором участвуют два вида энергии: потенциальная dE и кинетическая dE . Сопротивлением воздуха пренебрегаем, иначе надо добавить изменение энергии dE , предполагая какую-либо связь между диссипативными силами и инвариантом s или скоростью |v| . Уравнения движения и закон сохранения энергии примут вид (ось z направлена вертикально вверх)

x= а ,        y= Р ,       z =у-u ( У , t ) , d E +dE 0 .

Повороты отсутствуют, движение поступательное, энергию можно проинтегрировать по всему объему тела. Для приращений энергии E1 и E2 следует записать dE k dz 0 ,      dE   k2d(vz2)  k d(z2)  2k z z dt  2k z dz 0 , и, если использовать общепринятое обозначение для ускорения свободного падения z g , соотношение между коэффициентами должно быть k  2k g . В классической механике принято k mg , тогда k m/2 и для кинетической энергии получаем общепринятое выражение

E mv ² / 2 .

Свойства, определяемые коэффициентами k5 , k6, k7 , должны полностью определять энергетические изменения частиц в области обратимой деформации. Свойства k8 , k9, k10 и инварианты , £ , 5 10 не вошли в уравнение энергетического баланса (14), учитывающего внешние воздействия, так как их производные по времени содержат множители типа x , которые не входят в выражение (12) для энергии внешних воздействий. Этого достаточно для утверждения, что они связаны с механизмами обратимой и необратимой деформации, учитывать их различие в глинах и сыпучих средах.

В процессе необратимой деформации условие энергетического баланса вместо (14) принимает вид со — тpixi,tp k5 ^5+ k6 ^6,t + k7 7,t +k11^11,t + k12^12,t + k13^13,t ,                 (27)

следовательно, диссипативные процессы связаны с параметрами , 5 , 13 и свойствами k11 , k12, k13 . Именно они определяют упрочнение, изменение механических свойств грунтов, специфику горных пород, энергетические особенности нарушения структурных связей между минеральными частицами и пр.

Так как излагаемая энергетическая модель должна учитывать возможные варианты движения от любых внешних воздействий, рассмотрим изменение энергетического состояния частицы из изотропного материала при равномерном нагреве. В соответствии с общепринятыми представлениями и понятиями, при нагреве на температуру АТ линейные размеры частицы изменяются на величину Т , где - коэффициент линейного расширения материала, при этом затрачивается энергия

Е Т с mdT

Т 0

или, приближенно, ЕЖ = ссрЖЕТ , ЕЖ/ Жо сссррТГ , где сср - средняя теплоемкость материала в рассматриваемом диапазоне температур от Т0 до Т. С учетом уравнений движения х = «г(1 + «ГАТ), деформаций Лагранжа ха = (1 + атЕТ) и приращений инвариантов Мх = 3атТТ , U2 = 6атТТ + 3(атТТ)2, М3 = ЪатТТ+3(«гТ))2+(атТТ)3 , условие перехода подведенного тепла в энергию частицы принимает вид ср0 / ат - 3к5 + 6к6 + 3к7 + 3(к6 + к7 )атТТ к((атТТ)2 « 3(к5 + 2к6 + к7).  (33)

Сравнивая правые части уравнений (20) и (33), можно утверждать, что средние напряжения в исходном состоянии следует считать равными

°"о| t= 0 = c А^/(3 «Т ⁾⁼ k 5+^{2 к} 6 + ^к 7 ,                                   ⁽³⁴⁾

где все физические характеристики в правой части должны соответствовать исходному состоянию материала, т. е. при нормальном давлении и температуре  200С.  По существу использование соотношения (34)

соответствует переходу к новой энергетической шкале средних напряжений, по аналогии с термодинамической шкалой температуры Кельвина.

В отличие от твердых однородных тел, например металлов, нагрев грунтов сопровождается изменением, пористости, влажности и водопроницаемости. Поэтому в зависимости от диапазона температур уравнение (34) должно быть дополнено слагаемыми, учитывающими энергетические характеристики этих изменений.

Для определения каждого из коэффициентов правой части уравнения (20) достаточно дополнительно двух уравнений, например по результатам испытания на чистый сдвиг и гидростатическое сжатие. В качестве основного принимаем общее уравнение (19) для среднего напряжения

3 aR = k 5£5+2 к 6^6+3 к 7^7, которое можно привести к обычной шкале средних напряжений за счет сдвига шкалы на величину исходных напряжений (20), т. е. в обычной шкале зависимость среднего напряжения Коши от инвариантов тензора деформации принимает вид

<~ = (г - (Г_о = ( к₅^₅ + 2 к^₆ + 3 к^ ₇) /3 R - ( к ₅ +2 к₆ + к ₇) = к₅

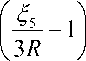
+ 2 к 6

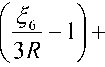
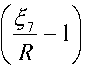
В условиях однородного гидростатического сжатия с уравнениями движения х = аД + 8) = e_te , 3₅=3е, 6=3е ², <^₇= е³ и R = ^=e³ получаем <~ = (1— е )[ к ₅ (1 + е ) + 2 к₆е ]/ е ² . С другой стороны, из закона упругого изменения объема

<~ = 3K(R 1/3-1) = 3K(е -1)/е2. (36) Приравнивая правые части последних двух уравнений, получим k (1 + e) + 2k e 3К(37)

или, принимая во внимание е 1 , k+ k 1,5К .(37а)

При чистом плоском сдвиге уравнения движения имеют вид х = a + 9(3 ,          у = a9-v (3 , где 6 - угол сдвига. Два инварианта сохраняют исходные значения, меняется только квадратичный инвариант     I 3,  ^I3+292,

I 1  . Работа внешних сил E = JdY =GJ^dY = 0,5GY2  должна соответствовать изменению энергии материала E k A^ 2k Y 2 . Из энергетического баланса для обратимого процесса получаем k6   1 G .                                          (38)

Важно, чтобы величина G была определена с помощью описанного эксперимента, а не вычислена через модуль Юнга и коэффициент Пуассона. Отрицательный знак коэффициента k объясняет увеличение энергии частицы при уменьшении ее объема за счет гидростатического сжатия.

Энергетическая модель механики позволяет обосновать существование новых физических свойств грунтов, возможность перехода к новой шкале средних напряжений, по аналогии с термодинамической шкалой температур, а также целесообразность исследования их влияния на изменение структурных связей между минеральными частицами, формирование дисперсных образований и пр.