Энергетическая модель никель-водородных аккумуляторов

Аккумуляторные батареи (АБ), предназначенные для работы в составе системы электроснабжения (СЭС) космических аппаратов (КА), должны удовлетворять ряду требований, из которых основными являются высокая надежность, длительный срок службы (не менее 15 лет), высокое значение удельной энергии, малый ресурсный спад удельных характеристик при числе циклов заряд-разряд (до 4 • 10 ³ ), достаточно широкий интервал рабочих температур (0.. .40 °С), механическая прочность (стойкость к перегрузкам в сочетании с виброперегрузками, имеющими место на этапе выведения КА на орбиту), возможность работы как при отсутствии силы тяжести, так и при любой пространственной ориентации, минимальный саморазряд, малое внутреннее сопротивление и т. д.

В настоящее время благодаря высокой удельной энергии и большому циклическому ресурсу основное место среди химических источников тока (ХИТ) для космических программ прочно завоевали никель-водородные аккумуляторы (НВА). По сравнению с другими электрохимическими системами эти аккумуляторы имеют ряд особенностей, которые необходимо учитывать при их исследовании, эксплуатации и математическом моделировании:

• -    наличие двух неразделенных активных газов (кислорода и водорода) в общем объеме, что создает при перезаряде и смене полюсов потенциальную возможность инициирования внутри НВА взрывоопасной кислородно-водородной смеси;

• - высокая удельная энергия (55.. .60 Вт • ч / кг), которая получается за счет применения разнополярных электродов несоизмеримых толщин. Водородный электрод является лишь местом токообразующей реакции, а не хранителем активной массы - водорода;

• -    высокая концентрация энергии в малом объеме сопровождается повышенным тепловыделением в единице объема. Повышенная температура существенно снижает ресурс работы НВА, емкость и энергию, отдаваемую на разряде в нагрузку;

• -    заряженный НВА термодинамически нестабилен, т. е. при хранении в заряженном состоянии емкость теряется за счет саморазряда. Эти потери реализуются в виде дополнительного внутреннего тепловыделения. Величина саморазряда в значительной степени зависит от температуры НВА, нелинейно увеличиваясь при ее повышении. Это свойство НВА мало сказывается при постоянном циклировании аккумулятора, однако оно должно учитываться при перерывах в работе и оценке теплового режима НВА в батарее;

• -    при заряде НВА в изохронно-изотермических условиях (примерно до 80 % номинальной емкости) наблюдается линейная зависимость между давлением в аккумуляторе и степенью заряженности. Эта уникальная осо

бенность НВА позволяет непосредственно по тензометрическим показаниям определять текущую степень заряженности аккумулятора;

• -    тепловыделение НВА и связанные с ним токовые потери на побочные реакции при заряде, потери энергии на заряде и разряде, КПД по емкости и по энергии, степень заряженности и другие характеристики существенно нелинейно зависят от условий циклирования (токов заряда-разряда, температуры, степени заряженности);

• -    при сообщении НВА полной зарядной емкости давление газа внутри корпуса достигает максимального значения и в процессе дальнейшего заряда (перезаряда) давление стабилизируется. Это свойство НВА, допускающего длительный перезаряд, используется для упрощения схемы контроля степени заряженности, но при этом вся избыточная энергия перезаряда превращается в тепло, т. е. заряд идет с нулевым КПД и температура аккумулятора повышается. Такой режим работы НВА в принципе не является аварийным, но он крайне не желателен.

Математическое моделирование СЭС КА предъявляет повышенные требования к математической модели применяемого в ней химического источника тока в силу особой специфики функционирования КА в космосе. В первую очередь, это автономный режим работы КА на орбите, широкие границы изменений условий функционирования (температуры, разнообразия сеансных расписаний нагрузок, условий охлаждения, режимов полета, параметров орбиты, мощности нагрузки, большого числа циклов и др.), высокие требования к надежности и долговечности КА.

Несмотря на довольно большое количество разработанных математических моделей ХИТ, многие из них имеют ограниченное применение и малопригодны для математического описания ХИТ как элементов СЭС КА в связи со следующими условиями:

• -    они в основном ограничиваются описанием только разрядных характеристик ХИТ, хотя условия заряда оказывают существенное влияние на зарядные характеристики и циклы заряда-разряда необходимо рассматривать как единое целое;

• -    используется ограниченный экспериментальный материал, когда описываются внешние характеристики ХИТ в функции емкости при нескольких фиксированных значениях температуры (обычно 20 ... 25 °С) и токов заряда-разряда, что не позволяет рассчитывать характеристики ХИТ при плавном изменении температуры в процессе циклирования, так как в них исследуются только частные режимы циклирования ХИТ;

• -    формулы, описывающие зарядно-разрядные характеристики ХИТ различных электрохимических систем, носят полуэмпирический характер, что затрудняет рас-

• пространение полученного математического описания на широкую область изменения нескольких рабочих параметров, так как методики определения эмпирических коэффициентов сложны и недостаточно подробно описаны в литературе;

  - в этих моделях обычно рассматриваются зависимости электрических и других характеристик от сообщенной или отданной в нагрузку емкости, хотя разработчиков СЭС КА больше интересуют зависимости по энергии, так как при решении задач энергобаланса СЭС КА приходится рассматривать распределение потоков энергии между первичным (солнечной батареей) и вторичным (аккумуляторной батареей) источниками электроэнергии и нагрузкой в соответствии с сеансным расписанием.

Для решения задач, стоящих перед разработчиками СЭС КА, необходима энергетическая модель ХИТ, позволяющая рассчитывать текущее энергетическое состояние источника при циклировании по произвольным частным и предельным циклам при известных условиях конвективного или радиационного теплообмена. Поскольку ХИТ любой электрохимической системы является сложным, существенно нелинейным, многопараметрическим объектом и многие его внешние характеристики взаимосвязаны и взаимозависимы, то необходимо применять комплексный подход к моделированию всех внешних характеристик ХИТ как функции определенного набора параметров. Это может значительно сократить время и затраты на проведение экспериментов и математическое моделирование в целом.

При разработке энергетической модели НВА авторы исходили из того, что для аккумулятора как преобразователя энергии, подводимой к нему на заряде, в энергию активных масс электродного блока и обратно в электроэнергию в процессе разряда (рис. 1), будет выполняться закон сохранения энергии:

W₃-W _1T - W _3T- W_p-W . O, (1) где W - энергия, получаемая от зарядного устройства; W _it - энергия тепловых потерь на заряде; W _рт - энергия тепловых потерь на разряде; W _р - энергия, отдаваемая в нагрузку; W _зст - остаточная энергия.

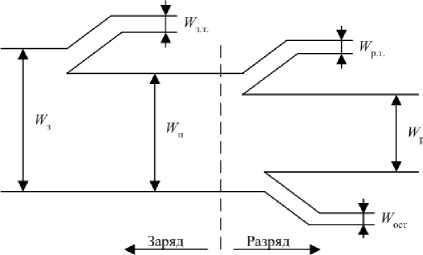
Рис. 1. Распределение потоков энергии в цикле заряд-разряд

Формализованную с точки зрения электрохимии энергетическую модель НВА можно записать в виде системы:

Q 3               ^т з                Q Р               ^Т р

J U ₃ dQ - J N„ d т = J U _р dQ + J N _р , _т d т + W , (2)

00 00

^Т 3

Q з — J I з d т ,                     (3)

^т Р

Q_n = Id т р р

^W з=т =/( ^Т,1 Д (5) где U _з - напряжение на аккумуляторе в процессе заряда; U _р - напряжение на аккумуляторе в процессе разряда; I _з - ток заряда; 1 _р - ток разряда; N _зт - мощность тепловых потерь на заряде; N _рт - мощность тепловых потерь на разряде; Q _з - зарядная емкость; Q _р - разрядная емкость; Т _з - температура аккумулятора; т _з - время заряда; т _р -время разряда.

Однако при использовании формализованной эмпирической модели как в процессе эксперимента, так и в дальнейшем, при штатных условиях эксплуатации, измеряется и контролируется одна и та же величина - темпе ратура корпуса аккумулятора, поэтому принятое допу щение, при котором температура корпуса приравнивается к температуре аккумулятора вообще, остается справедливым лишь для ограниченных условий теплообмена. Под этим следует подразумевать, что теплообмен может осуществляться либо за счет принудительной цир куляции газа-теплоносителя внутри гермоконтейнера КА:

dT

Nт - mC —— + Fа(T -To), либо при теплообмене d т только излучением, например при установке аккумуляторной батареи вне гермоконтейнера: Nт — mC~т^ + о(T - Тр), где Nт - мощность тепловыделения на заряде и разряде; С-удельная теплоемкость ак кумулятора; m - масса аккумулятора; Т^ - температура окружающей среды (газа-теплоносителя); а-удельный коэффициент теплоотдачи; F - площадь теплоотдачи; о - коэффициент лучеиспускания; Тр - равновесная температура аккумулятора (при расположении вне гермоконтейнера).

Энергетическая модель НВА, как всякая эмпиричес кая модель, справедлива только в тех границах, для которых она составлена, поэтому при проведении экспериментальных исследований указанные границы задавались таким образом, чтобы осуществлялось перекрытие факторного пространства, а сами исследования проводились методом планирования эксперимента.

Во время экспериментов факторам (первичным параметрам, в данном случае току заряда-разряда и температуре) последовательно задавались различные сочетания значений, а получающиеся при этом в установившихся режимах значения выходного параметра (напряжения заряда-разряда и мощности тепловыделения) фиксировались. Поскольку определение функции отклика в общем случае велось при неполном знании механизма явления, а аналитического описания при этом, естественно, не имелось, то пришлось ограничиться представлением функции отклика полиномом третьей степени. Хотя полиномиальная форма не является наилучшей, но по сравнению с моделью, основанной на схеме замещения [1], формализованная энергетическая модель имеет принципиальные преимущества:

• -    она позволяет осуществлять определение текущего состояния НВА при его работе как по полным, так и по частным циклам;

• -    выражения, описывающие потери текущей мощно

сти и тепловыделения на заряде и разряде, позволяют ко- личественно оценить ту часть тепловой нагрузки на систему терморегулирования (СТР) КА, которая приходится на аккумуляторную батарею, что, с учетом ее значительного вклада в общее тепловыделение, дает возможность обоснованно выбрать технические характеристики СТР.

Следует отметить, что моделирование энергетических, а значит, и тепловых процессов, сопровождающих работу АБ при ее циклировании с произвольной глубиной, является важнейшей задачей при разработке СЭС КА [2].

Моделирование текущего состояния НВА сводится к нахождению остаточной энергии W при известной потребной энергии разряда W _з , обусловленной нагрузкой, и вычисленной в зависимости от режима работы энергией тепловых потерь на разряде W (см. рис. 1). Это можно сделать в том случае, если известна полезная запасенная в аккумуляторе энергия W , которая, в свою очередь, является разностью между энергией, подводимой от зарядного устройства, W ₁ и энергией тепловых потерь на заряде W . Текущая величина W может изменяться в пределах W < W _л <  W . Максимальная полезная энергия W обусловлена количеством активных масс электродного блока НВА. Следовательно, величина W в пределе может стремиться к W , т. е. после того как исчерпается возможность преобразования энергии в результате физико-химической реакции в активных массах (режим перезаряда), вся подводимая от зарядного устройства энергия будет выделяться в аккумуляторе в виде тепла W .

Отмеченные выше предельные режимы работы не имеют места в реальных условиях эксплуатации НВА и приведены здесь исключительно для иллюстрации физических закономерностей при их работе. Так, например, величина W _з ограничена допустимым минимальным на

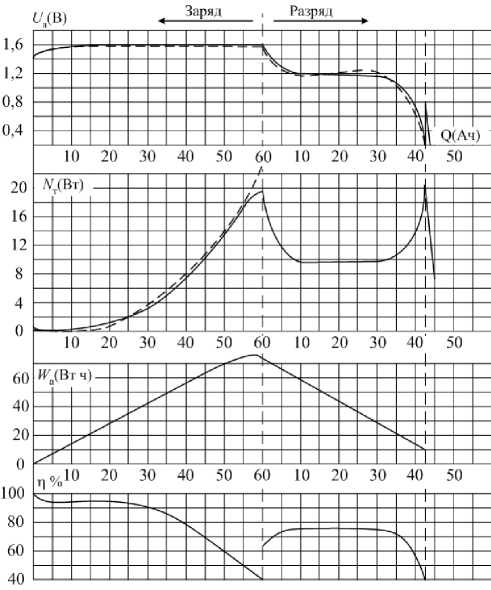
Рис. 2. Зарядно-разрядный цикл: Nг - мощность тепловыделения; W1 - энергия; п - КПД пряжением на одном аккумуляторе при заряде (0,5_0,6В). Режим бесконечно большого перезаряда (когда W1т ^ WJ, являясь энергетически неэффективным, может привести к взрыву НВА, так как даже при заряде до номинальной емкости его корпус испытывает избыточное давление порядка 110.. .120 атм.

Проведенные исследования НВА типа НВ-40 в следующем диапазоне варьирования основных параметров: температура - 0.. .45 °С, ток заряда - 2_20А, ток разряда - 4^28А, зарядная емкость - 0_60А • ч позволяют определить необходимые зависимости, которые для одного из режимов приведены на рис. 2.

Проведя анализ кривых (см. рис. 2) можно сделать вывод, что значительная величина и существенная нелинейность мощности тепловыделения, оказывающая большое влияние на эффективность эксплуатации НВА в составе СЭС КА, определяют целесообразность применения энергобалансной модели НВА [3].

Поскольку определение эффективности режима заряда при представлении W _1т в абсолютных величинах имеет малую наглядность, на рис. 3 зависимости мощности тепловыделения приведены в относительных единицах N / Р , где Р - мощность на выходе зарядного устройства.

Таким образом, по полученным экспериментальным кривым зарядно-разрядных характеристик можно с помощью численного интегрирования определить значения всех зависимых переменных (рис. 4,5).

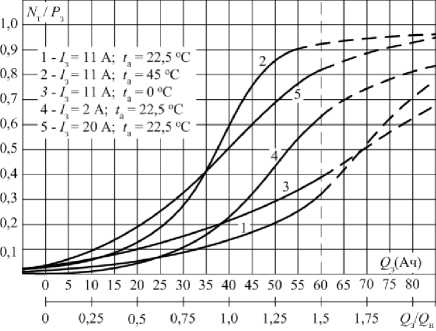
Рис. 3. Влияние режима заряда на эффективность использования энергии

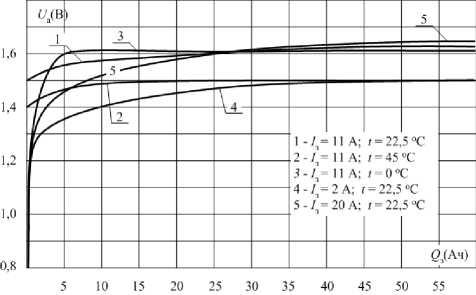
Рис. 4. Семейство зарядных характеристик НВА для некоторых режимов

Полиномиальная математическая модель НВА представляется следующей системой уравнений:

N _зт = a о + a ₁ x з + a ₂ x з + a ₃ x 3

a 0 = 1,317 0 + 0,710 6 x . + 0,644 0 x ₃ + 0,093 3 x . x ₃ + + 0,326 9 x 1 ² + 0,118 3 x ₂ ² - 0,0321 x . - 0,032 4 x 3 , a₁ = 1,359 8 + 0,446 x ₁ + 0,595 7 x ₃ + 0,0531 x ₁ x ₃ +

• ■    + 0,232 6 x 2 + 0,107 7 x ₂ ² + 0,020 2 x ³ - 0,010 9 x 3 , a ₃ = 0,516 9 - 0,073 7 x ₁ + 0,157 0 x ₃ + 0,024 7 x ₁ x ₃ -- 0,012 4 x 2 + 0,006 0 x ₂ ² + 0,013 9 x 3 + 0,001 6 x 3 , a, = 0,066 0 - 0,048 5 x. + 0,002 2 x, - 0,003 1 x.x, - 31212

  - 0,0221 x 2 - 0,006 4 x ₂ ² + 0,000 1 x 3 - 0,000 9 x 3 ,

Uз = b о + b1 x3 + b 2 x2 + b3 x3, b0 = 1, 567 3 - 0,023 2x- + 0,022 0x3 + 0,0015x x3 --0,002 5x2 - 0,003 8x22 + 0,0011x3 + 0,000 3 x23, b1 = 0,017 6 - 0,007 3x1 - 0,007 0x2 + 0,0019x1x2 -

• ■    - 0,002 5 x 2 - 0,000 1 x 2 + 0,000 8 x 3 + 0,000 3 x ₂³, b ₂ = - 0,005 4 + 0,000 4 x ₁ - 0,000 6 x ₂ + 0,0001 x ₁ x ₂ + + 0,0001 x 2 - 0,000 5 x 2 - 0,0001 x 3 ,

  b = 0,000 3 + 0,000 4 x . + 0,000 3 x, - 0,000 2 x. x, + 31212

+ 0,0001 x 2 + 0,000 2 x 2 + 0,0001 x ₂³,

1дех1 = 0,125 4(t - 22,5);х2 =0,313 6(I- 11);х3=0,09407(g3- 30); Nр.т = cо + c x 3 + c 2 x2 + c3 x3, c0 = 5,813 7-0,414 0x1 +1,9613x2 -0,090 6x1 x2 + +0,200 2x2 + 0,005 4x22 + 0,040 9x3 - 0,042 9x3, c1 = -0,5110 - 0,277 1x1 + 0,293 9x2 - 0,059 8x1 x2 +

• ■    + 0,124 9 x 2 - 0,000 7 x ₂ ² + 0,028 2 x 3 - 0,042 5 x 2 , c ₂ = 0,212 3 - 0,012 x ₁ + 0,055 6 x ₂ + 0,003 0 x ₁ x ₂ + + 0,015 9 x 2 + 0,0031 x 2 + 0,006 7 x ³ + 0,0015 5 x ₂ ³, c ₃ = 0,137 2 + 0,330 x ₁ - 0,009 2 x ₂ + 0,004 5 x ₁ x ₂ -- 0,006 3 x 2 + 0,002 7 x 2 - 0,002 3 x ³ + 0,0061 x 3 ,

  U p = ( d , - d ₂ a ) { ¹ - exp [ d ₃ ( Q - Q _рк ) ] } + d ₄ exp ( - d ₅ Q ) , d ₁ = 1,243 7 + 0,034 9 x - 0,273 x ₃ + 0,001 5 xx ₃ -- 0,002 9 x 2 + 0,005 9 x 2 - 0,000 9 x 3 - 0,000 7 x 3 , d ₃ = 0,002 1 - 0,000 12 x ₁ + 0,000 037 x ₃ - 0,000 33 x ₁ x ₃ + + 0,000 59 x 2 + 0,000 03 x 3 , d = 0,744 3 + 0,094 6 x, - 0,105 2 x ₂ - 0,017 0 x,x ₂ - 31212 - -0,014 7 x 2 + 0,002 5 x ₃ ³ - 0,025 9 x 3 - 0,003 9 x 3 , d ₄ = 0,228 2 - 0,0401 x ₁ - 0,003 0 x ₃ - 0,003 2 x ₁ x ₃ -- 0,003 8 x 2 - 0,003 6 x ₃ ³ - 0,005 4 x 3 + 0,005 7 x ₃³, d. = 0,604 3 + 0,159 6 x, - 0,204 5 x ₂ - 0,044 1 x, x ₂ + 51212 + 0,008 2 x 2 - 0,004 6 x ₃ ³ - 0,020 4 x 3 + 0,017 4 x ₃³, Q _pK = 40,790 6 - 0,698 5 x , + 0,167 4 x ₂ + 0,613 7 x , x ₂ -- 1,360 2 x 2 - 0,027 7 x ₃ ³ - 0,240 4 x 3 + 0,128 4 x ₃³,

где х ₁ = 0,125 4(t- 22,5); х ₂ =0,235( / _р - 16); x ₃

5, 644

Q p. ( Q з - 30 ) '

В систему уравнений входит конечная разрядная емкость Q _{р к} , которая в описываемой серии экспериментов зависит от токовых и температурных режимов циклирования и изменяется от 42,5 до 24,8 А • ч. Поскольку жесткой границы варьирования зарядной емкости установить нельзя, было составлено уравнение регрессии, по которому вычислялось значение конечной разрядной емкости 6 р^ ^-,^ ( Т ^(рис.⁶).

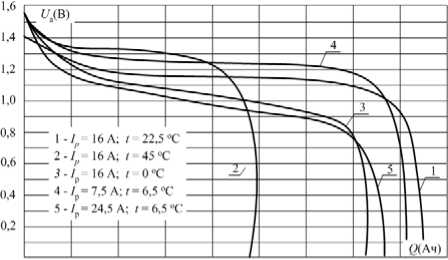
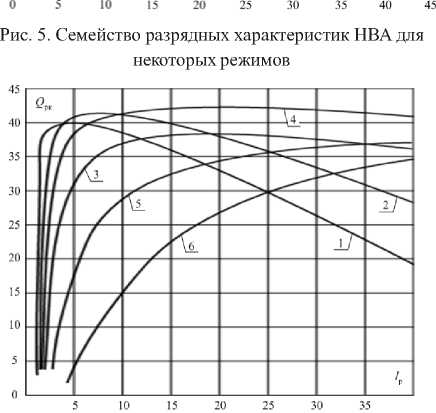
Рис. 6. Зависимость конечной разрядной емкости от температурного и токового режимов: при t = 0°С (1); t = 6,5 °С (2); t = 14,5 °С (3); t = 25 °С (4); t = 38,5 °С (5); t = 45 °С (6)

Энергетическая циклограмма, поясняющая работу формализованной модели НВА, приведена на рис. 7.

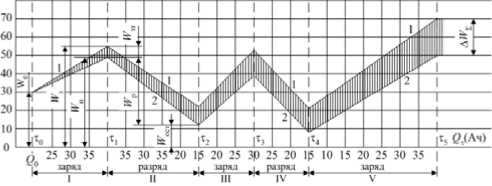
Рис. 7. Зарядно-разрядная энергетическая диаграмма

Таким образом, разработанная энергетическая модель НВА, описывающая параметры его текущего состояния при циклировании по произвольным предельным и частным циклам в условиях конвективного и радиационного теплообмена, позволяет производить расчет энергетического состояния НВА в СЭС КА и определять оптимальные режимы заряда. По результатам моделирова- ния НВА определены алгоритмы управления зарядным током, максимизирующие КПД заряда, что позволяет дополнительно запасти на 10^15 % больше полезной энергии по сравнению с зарядом постоянным током, также выявлен диапазон температур (от 10 до 30 °C), в котором НВА обладает наилучшими характеристиками.