Энергетическая релаксация в гетеродинных детекторах на основе двумерных электронных систем

Одной из актуальных проблем современной радиофизики является получение изображений в терагерцовом диапазоне частот. Этот диапазон имеет преимущества, по отношению к радиоволнам и инфракрасному излучению. Первые не обеспечивают достаточного пространственного разрешения из-за. большой длины волны, второе сильно поглощается атмосферой, кожей, одеждой и т.д. В этом диапазоне наилучшими характеристиками, в том числе шумовой температурой, обладают охлаждаемые до гелиевых температур смесители на основе перехода сверхпроводник-изолятор-сверхпроводник (СИС-смесители) и смесители (болометры) на горячих электронах [1].

Принцип действия гетеродинного смесителя основан на. выделении сигнала, на. частоте, соответствующей разности частот излучения от исследуемого объекта, и гетеродинного источника. Если частота, излучения объекта, находится в терагерцовом диапазоне, частоту гетеродина, подбирают таким образом, чтобы разностная частота, составляла, не более нескольких ГГЦ. Метод гетеродинного детектирования реализуется в различных сверхпроводниковых и полупроводниковых структурах вследствие нелинейности их вольт-амперной характеристики (ВАХ) из-за. разогрева, носителей током и электромагнитным излучением. При фононном охлаждении горячие электроны изменяют свою подвижность вследствие передачи энергии фононной подсистеме. В случае энергетической релаксации носителей в контактах нелинейный характер ВАХ-детектора, обусловлен сопротивлением контактов, а. время энергетической релаксации носителей определяется скоростью их диффузии в контакты. Таким образом, при постоянной концентрации носителей возникает фотопроводимость на. промежуточной частоте. Сигнал промежуточной частоты детектируется в полосе преобразования /з^в, которая определяется временем неупругого рассеяния электронов в структурах: /зав = 1/ (2ттт_е).

Гетеродинные смесители успешно работают в таких проектах, как HERSHEL, SOFIA, TELIS. Они используются в качестве активного элемента, детектирующего реликтовое излучение Вселенной. В задачах астрономических наблюдений особый интерес представляет исследование вращательных переходов HD на. частоте 2.7 ТГц и тонкой структуры переходов в спектре атомного кислорода, около 4.7 ТГц. На частотах менее 1.4 ТГц наилучшей чувствительностью обладают СИС-смесители, в области более высоких частот используются смесители на эффекте электронного разогрева в тонкой пленке сверхпроводника [2]. СИС-смесителям требуется более высокая мощность гетеродинного источника (~ 10 Вт) по отношению к тонкопленочным сверхпроводниковым смесителям (~ 1 Вт). Широко распространено применение смесителей на сверхпроводниковых наноструктурах NbN, при этом в качестве гетеродинного источника работают квантовые каскадные лазеры [3, 4]. Такие комплексы для гетеродинного детектирования характеризуются низкой шумовой температурой ~ 800 К, малой мощностью гетеродина (до ~ 6 мВт) и широкой полосой преобразования б ТГц.

В качестве альтернативы смесителям на горячих электронах в сверхпроводниках предложены гетеродинные смесители с фононным каналом охлаждения носителей на основе наноструктур с двумерным электронным газом AlGaAs/GaAs [5]. Полоса преобразования таких смесителей определяется при гелиевых (азотных) температурах релаксацией носителей на акустических (оптических) фононах соответственно. Как показано в [б], полупроводниковые смесители характеризуются достаточно низкими мощностью гетеродина и коэффициентом потерь преобразования при широкой полосе преобразования. Для структуры с концентрацией n_s = 3 • 10¹¹ см^-2 и подвижностью электронов ц = 2.3 • 105 см²/Вс при Т = 77 К эти параметры составляют 0,2 мкВт, 13 дБ и 4 ГГЦ соответственно.

Целью настоящей работы является теоретическое исследование механизмов энергетической релаксации и параметрических зависимостей времен энергетической релаксации электронов в двумерных полупроводниковых структурах в квантово-упорядоченном состоянии и квантовой критической области, а также поиск оптимального решения для полосы преобразования смесителей с фононным и диффузионным каналами охлаждения электронов на основе полупроводниковых наноструктур.

Наряду с фундаментальным значением предлагаемых исследований, которые значительно дополнят и расширят понимание процессов разогрева электронного газа в гетероструктурах излучением миллиметрового и субмиллиметрового диапазонов, решат принципиально новые задачи изучения релаксационных процессов в полупроводниковых системах пониженной размерности, результаты работы имеют и прикладную направленность. Они будут использованы для оптимизации полупроводниковых супергетеродинных приемников излучения на базе болометров на горячих электронах: для расширения рабочего диапазона частот смесителя терагерцового диапазона, уменьшения требуемой мощности гетеродина. Кроме того, решение задач по оптимизации смесителя на основе полупроводниковых наноструктур позволит прогнозировать создание многоэлементных (матричных) приемных элементов, необходимых, например, в системах субмиллиметрового тепловидения, интенсивно разрабатывающихся в настоящее время, а также в радиотелескопах и системах мониторинга.

Модель

Модель смесителя с двумерным электронным газом рассматривает двумерный газ как термодинамическую подсистему, которая локально характеризуется распределением Ферми с температурой Т_е и передает избыточную энергию фононной подсистеме - термостату, находящемуся при температуре Т. Электронная подсистема нагревается сигнальным и гетеродинным источниками, а также током смещения. Для вычислений динамического одномерного профиля распределения электронной температуры Т_е (ж, t) при известной температурной зависимости сопротивления мостика R (Т_е (ж, t)) используется уравнение теплового баланса:

Се (Те (ж, t)) ^дТе^ = -Q (Те (ж, t) , Т ) - Се (Те (ж, t)) Х^^ ^ ⁺ ^ “ t) ^R (Те (ж, t)) +

+ PLO + Ps + 2^PloPs cos(2Tr/t), где Се - электронная теплоемкость, Q - скорость потерь энергии неравновесными электронами, обусловленная электрон-фононным рассеянием, х ~ коэффициент диффузии го рячих электронов, Imix - постоянный ток, протекающий через смеситель, Plo и Ps -мощности гетеродина и сигнала соответственно, f - промежуточная частота. Слагаемое Се (Те (ж, t)) х^—д^т^) описывает диффузию горячих электронов в контакты.

В приближении Plo,Ps << imгх^ рассмотрим два предельных случая. Первым из них является охлаждение горячих электронов за счет передачи энергии фононному тер мостату, которое реализуется в достаточно длинных мостиках. При этом средняя скорость потерь энергии горячими электронами в области низких температур зависит от характера рассеяния. Если волновые векторы фононов, эмитируемых в направлениях параллельно и перпендикулярно проводящему каналу, ограничены температурой, мы находимся в области малоуглового рассеяния кТ << ^ Bms^E р, г де Ер - энергия Ферми, m - масса носителя, s\ - скорость продольной (s) или поперечной (sp) моды звука. В этой области средняя скорость энергетических потерь нагретого до температуры Те газа Ферми получена в [7, 8] для рассеяния на пьезоакустическом потенциале (РА):

(Qf^A = biQi

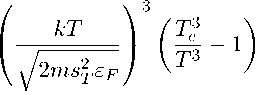
и для рассеяния на деформационном потенциале (DA):

<^Q>^DA = ^ ⁽ ) ² (72^ У ^{(T5 -} 1 ) ,

где

bi = ^y^13 1 + 9 (—) 1 Для орпептапіш

2 16      13 \ s

(001) ,

bi = ?(3) -5 1 + 11 (—) для орпептапіш

12 [     10 \ s / J

(111) ,

Qi = 2m£,

то 1

то

_ (еН)² m 2р р~² sp ¹

Н = ^14 - компонента пьезоэлектрического тензора,

. .      _      2ms2

b2 = 12y(5),   Q2 = ——, lo = ^~4p/2m3E2, lo/s

Ei - константа потенциала взаимодействия, p - плотность трехмерной матрицы.

В области частичной неупругости характерная энергия фононов, испускаемых или поглощаемых двумерным электроном при его движении вдоль канала, составляет ~ кТ (неупругие переходы). Этот процесс, удовлетворяющий законам сохранения энергии и импульса, и определяет релаксацию энергии. В этой области средняя скорость энергетических потерь газа Ферми [7, 8]

(Q)pa

9 кТ 12ms² ГТ_е

2 х V . Тт

-

для ориентации (001) ,

р'"

= < (2)4 ⁸т (Pt

3 s ТоЕр

⁽ Т2 т ²

-

для ориентации (111) ,

;„- ..ЩДT4 .у

РТ- Т = £ (2^)2.

В области высоких температур энергия фононов, испускаемых или поглощаемых дву

мерным электроном при его движении вдоль канала, составляет ~

^8ms²_xW. где W -

энергия размерного квантования. Средняя скорость потерь энергии получена в [7, 8] для

пьезоакустического рассеяния в ориентации (001)

та™=9 - J^ ( t ? - 1), ² То у Ер \1

для ориентации (111)

PA 3 kT 'J^2mT^W (T?   '

(0)  = 41оЕр —ТО— Ут -*, для рассеяния на деформационном потенциале

(Q)DA

т 2ms2 W T? -T

12--7--Т—

ТзЕр    T

где Тз =

10 (2ms²)³/²

^2s kT VW "

Используя значения волновой функции Фэнга-Ховарда для основного состояния, получаем

12 = 332-5т-2,

1о = 3/8,

( 11 )2/3   (ЕР

^W =   уза)   ^Ер Ы ,

где Ер ^ боровская энергия.

Режим сильного экранирования характеризуется средними скоростями потерь энергии [7, 8]:

(Q)^PA = у (5)4!а^ ЕҒ

где

а =

а =

(QfA

= (kT)⁷ • б!у (7) bDA 8^2фт^7/2Ер Ер^/286

(T7 О

1 59      45 zsj 41

32 64   + 59 ( s ) ]

_±И Г _А / s t А⁴] 32 12      11 s

для ориентации (001),

для ориентации (111),

bDA ^- численные множители, рассмотренные в [9].

Во втором случае, который характерен для коротких (длиной L <  1 мкм) мостиков, остывание горячих электронов происходит в контактах. Это т.н. диффузионный канал охлаждения двумерных электронов. Время ухода носителей в контакты тр = у)г, а соответствующая полоса преобразования /з^р = 1/ (2'ктр ) = х/ (2^L²).

Результаты и обсуждение

Результаты расчетов показывают, что для коротких ( L <  1 MKM)AlGaAs/GaAs мостиков в охлаждении преобладает диффузионный канал [10, 11]. При этом в образцах с высокой подвижностью д ~ 3• 105 см²/Вс при Т = 77 К и низкой концентрацией двумерных носителей ~ 2^1011 см^-2 для смесителя с площадью активной области 1x2 мкм² ожидается полоса потерь преобразования ~ 4 ТГц, что соответствует времени остывания 0.04 пс. Это значение сопоставимо с рекордными характеристиками сверхпроводниковых смесителей [12, 13] и, с учетом достаточно высокой рабочей температуры Т = 77 К, позволяет рассматривать AlGaAs/GaAs смесители с двумерным электронным газом как перспективную основу одиночных и матричных фотоприемников терагерцового диапазона массового производства. Однако и кремниевые МОП-структуры также могут служить основой широкополосных терагерцовых смесителей.

В работе [14] теоретически исследованы механизмы релаксации энергии электронов в кремниевой структуре с затвором в области температур Т = 1.5 ^ 3.5 К. Сопоставлением экспериментальной и расчетной параметрических зависимостей времени энергетической релаксации идентифицирован основной механизм релаксации энергии в этом температурном диапазоне - малоугловое рассеяние на деформационном потенциале. Соответствующее время релаксации, вычисленное на основе (1) с учетом среднего изменения энергии Ферми при перегреве электронного газа на АТ

AS =

тт²к²Т АТ Зер

составляет [14]

Т?А

8(тг87/2т3/2)2~^2ттр

1562^2 (кТ )³

Тогда величина полосы преобразования гетеродинного Si/SiO2 смесителя, ограниченная фононным каналом рассеяния, г ph J3dB

^^(кТ)3

16л3(з7/2т3/2)2~Д2^5

Полоса преобразования Si/SiO2 смесителя, определяемая диффузионным каналом, может быть существенно шире полосы /3р^_в- Причина этого заключается не только в возможности изготовления коротких мостиков - предел разрешения современной электронной литографии составляет около 50 нм [15]. Полосу преобразования смесителя можно существенно расширить, работая в квантовой критической области перехода металл-диэлектрик.

Вопрос о существовании квантового фазового перехода металл-диэлектрик в двумерной системе в пределе нулевого магнитного поля долгое время оставался дискуссионным. Тридцать пять лет назад ответ не вызывал сомнений: переход возможен и это переход Мотта-Андерсона. В 1979 г. ответ на этот вопрос был радикально изменен теоретической работой [16]. Авторы [16] использовали скейлинговый подход к анализу проводимости систем в приближении невзаимодействующих носителей. В соответствии со скейлинговой гипотезой логарифмическая производная безразмерного кондактанса д = 2~G/e² по размеру системы L при нулевой температуре является функцией только самого кондактанса. Для двумерных систем в отсутствие спин-орбитального взаимодействия данная производная отрицательна во всем диапазоне значений безразмерного кондактанса. Это означает, что при неограниченном увеличении размера системы ее кондактанс непрерывно уменьшается, т.е. двумерная система бесконечных размеров при нулевой температуре находится в диэлектрическом состоянии с нулевым кондактансом вне зависимости от того, как велик был стартовый кондактанс системы ограниченного размера. Электрон-электронное взаимодействие в грязном пределе дополнительно усиливает локализацию носителей [17].

Однако учет спин-орбитального взаимодействия изменяет локализационную поправку на антилокализационную [18]. Теперв, если стартовый кондактанс системы превышает критическое значение, линии потока переводят образец при неограниченном увеличении его размера в металлическое состояние. Посколвку двумерные системы из-за своего пограничного положения чувствительны ко всякого рода воздействиям, учет межэлектронного взаимодействия также должен привести к квантовому фазовому переходу металлдиэлектрик [19].

Впервые реминисценция квантового фазового перехода металл-диэлектрик в двумерной системе наблюдалась в работах [20, 21]. При измерении температурной зависимости сопротивления кремниевых МОП-транзисторов с двумерным электронным газом структуры с концентрацией электронов 6 10¹¹ см^-2 демонстрировали обычную для локализованных состояний отрицательную производную сопротивления по температуре: dR/dT <  0. Однако при некотором критическом значении электронной концентрации тс ~ 10¹¹ см^-2 сопротивление МОП-транзисторов обнаружило приблизительно температурно-независимое значение R ~ 2И/е2. Еще более неожиданным фактом оказалось резкое уменьшение сопротивления структур с электронной концентрацией n_s >  п_сс уменьшением температуры, наблюдавшееся вплоть до минимально достижимых в эксперименте температур 200 мК в отсутствие каких-либо признаков электронной локализации. Дополнительным подтверждением существования квантового фазового перехода металл-диэлектрик являлся наблюдавшийся скейлинг сопротивления в квантовой критической области по температуре:

R №h (^)

и электрическому полю:

R (^Е, тЭ = л (]т^)

с показателями степени г = 0.8 ± 0.1. ^ = 1.5 ± 0.1 [22].

Образцы на металлической стороне перехода обнаруживают довольно высокую (~ я^/е²) проводимость а, которая резко увеличивается с уменьшением температуры [23]. Учитывая соотношение Эйнштейна: а = е^дғХі ^гД^е дғ ~ плотность состояний на Ферми-уровне, получаем, что коэффициент диффузии в исследованных в [23] металлических МОП-структурах составляет ~ 105 м²/с. Такое высокое значение коэффициента диффузии может привести к терагерцовой ширине полосы преобразования даже в мостике длиной порядка сотен мкм.

Заключение

В работе выполнен обзор теоретических результатов исследования энергетической релаксации двумерных носителей в полупроводниковых структурах A3B5, A2B6 и составленных из элементов IV группы с кубической решеткой. Рассматривается средняя скорость потерь энергии электронов в результате рассеяния на фононах в областях сильного экранирования, малоуглового рассеяния, частичной неупругости и высоких температур, а также диффузионный канал охлаждения электронного газа.

С использованием модели теплового баланса установлено, что в коротких ( L <  1 мкм) AlGaAs/GaAs мостиках основным механизмом охлаждения является диффузия горячих электронов в контакты. Показано, что диффузионный канал может быть основным способом охлаждения и в металлических МОП-структурах. Выполнены оценки полосы преобразования в кремниевых мостиках с двумерным электронным газом на металлической стороне перехода металл-диэлектрик. Предполагаемая терагерцовая ширина полосы преобразования кремниевых гетеродинных смесителей в квантовой критической области фазового перехода в мостиках субмиллиметровой длины обуславливает перспективность их использования в соответствующих наземных и космических приложениях.

*Работа доложена на 5-й Всероссийской конференции молодых ученых «Микро-, нанотехнологии и их применение» им. Ю.В. Дубровского, ИПТМ РАН, Черноголовка, 19—22 ноября 2012 года.