Энергетические характеристики прохождения звуковой волны сквозь области скачкообразного изменения сечения волновода

ВЕСТНИК ПНИПУ. МЕХАНИКА № 3, 2024PNRPU MECHANICS BULLETIN

Многие задачи теории упругости, электродинамики и акустики в волноводах имеют между собой общность, благодаря которой методы построения аналитических решений данных задач во многом схожи [1]. Например [2], впервые решенное двумерное интегральное уравнения Винера – Хопфа может быть использовано в задачах распространения радиоволн, при конструировании элементной базы радиоэлектроники, в проблеме прочности в механике, в многочисленных других важных областях. Однако при детализации модели волновода, в частности при попытке учесть неоднородность по горизонтальной и вертикальной составляющей поля, задача уже не имеет аналитического решения даже в простейшем приближении, в этом случае используются численные методы для компьютерного моделирования акустических полей в волноводах. Численные методы, такие как метод конечных элементов, например [3], метод конечных разностей [4; 5] и др., и их разнообразные модификации [6–12], позволяют решать волновые задачи акустики для областей с геометрией любого уровня сложности. Несмотря на универсальность вышеперечисленных методов, принципиальным моментом численного моделирования волноводных процессов является вопрос корректности их приложения в каждом конкретном случае. В связи с этим, наряду с построением численных решений, в настоящее время активно развиваются численно-аналитические методы расчета полей, например [13–16], параболические приближения для плавно меняющегося рельефа дна [17–20].

Задача о распространении сигнала в волноводе является классической задачей теории нерегулярных волноводов. Для исследования данных волноводов исполь- зуется большое количество как специфических методов акустики, так и модификации хорошо известных подходов механики и математической физики. В простейших задачах рассматривается волновод с плоскопараллельными границами, для которого обычно можно найти строгое замкнутое решение [21–23]. В более сложных моделях широкое применение получил метод декомпозиции волновода на элементарные области [1; 24], где аналитические и численно-аналитические решения получаются из условий сопряжения решений в некоторых элементарных областях. При этом в задачах электродинамики оказывается возможным провести сшивку решений на основе метода факторизации [1], в то время как в задачах теории упругости и акустики [25] условия сопряжения приводят к бесконечным системам линейных уравнений.

Численно-аналитическая форма решения, обеспеченная использованием метода декомпозиции, позволяет значительно упростить исследование важнейшей характеристики звукового поля – потока энергии через сечение [25], так как в этом случае упрощаются операции, связанные с интегрированием функций по сечению волновода. Действительно, аналитическая форма полученного решения, дающая явные выражения для звукового поля на границе, позволяет найти энергетические характеристики прохождения звуковой волны через области скачкообразного изменения сечения волновода.

В работе проведены исследования энергетических характеристик акустического поля для типичного морского геофизического волновода с подводным выступом (впадиной). Подобный подход позволяет упростить численное моделирование и стать основой для дальнейшего исследования более сложной структуры дна.

Основные уравнения и структура общего решения задачи

Начало цилиндрической системы координат расположим на поверхности волновода над точечным источником звука с координатами (0, z 0 ), ось Oz направлена ко дну. Разобьем волновод на две области цилиндрической формы, каждая из которых характеризуется скоростью звука c j ( z ) и постоянной глубиной h j ( j = 0, 1). Выступ моделируется, если выполняется условие h 0 <  h 1 , радиус основания цилиндрического выступа при этом r 0 , а высота ( h 1 – h 0 ) (рис. 1). Звуковое поле в волноводе определяют [1; 21] амплитуды потенциалов скоростей Φ j в каждой из частичных областей, которые удовлетворяют уравнению Гельмгольца (1)

Рассмотрим решение краевой задачи для уравнений (1) в виде суммы нормальных мод. Каждая нормальная мода представляет собой решение вида ф(z; ^)v(5r), где § - константа разделения, которую принято называть «горизонтальным волновым числом». Подставляя это выражение в однородное уравнение Гельмгольца, и, разделяя переменные, получим для ψ следующее дифференциальное уравнение д2 v 1 ду   2 л

—7 + —— + §² у = 0 .

д r ² r д r

Как известно, решение данного уравнения имеет вид у = Ci H01) (§ r) + С2 J0(§ r),              (2)

^ЛФ 0 + -г- ^ф о = c ²( z )

§( z - z оЖ r ) 2π r

и Л Ф 1 + — Ф 1 = 0,(1) c ²( z )

где Л =

где H ₀ ⁽¹⁾ (ξ r ) , J ₀ (ξ r ) – функции Ханкеля и Бесселя нулевого порядка. При этом в неограниченной области волновода решение, описывающее уходящую от излучателя волну, можно записать как у = H 01 (§ r ).

Для функции φ(z; ξ) с учетом условий на горизонтальных стенках волновода получаем в ограниченной области (0) и неограниченной области (1) (рис. 1) следующие краевые задачи соответственно

д2 , 1 д , v

—- +----1--т— оператор Лапласа, о - дельта- дz2 r д r д r2

д

функция Дирака, й - круговая частота источника звука.

r 0

h 0

h 1

Рис. 1 Волновод с выступом

Fig. 1. Waveguide with protrusion

z

d Ф I Г г?!

-ГТ + 1“ - § IФ = 0, Ф(0, §) = 0, у( h 0, §) = 0. (3) dz   уc      J d^ + f- §21Ф = 0, Ф(0,§) = 0, d^(hi,§) = 0. (4) dz   у c      J

В качестве граничных условий используем условия того, что поверхность волновода является абсолютно мягкой, а дно и выступ являются абсолютно жесткими:

Ф ( r ,0) = 0

дФ д z

= 0

z = h 0

^{( r} <  ^r 0 ) ,

дФ

д z

= 0

z = h i

^{( r} >  ^r 0 )

дФ д r

= 0 ( h 0 <  z <  h 1 ) .

В первом приближении эти условия соответствуют условиям на поверхности и на дне для природных акустических морских волноводов. При этом в неограниченной области при r ^® для потенциала скоростей должно выполняться [1] условие излучения (условие Зоммерфильда)

г~ ( д Ф i ® Ф lim r r - I--- ^r ^» 13 r c

Данные краевые задачи являются задачами Штурма – Лиувиля и, как следствие, имеют дискретный спектр. Обозначим собственные функции задач (3) и (4) как φ _{0 n} ( z ) и φ _{1 n} ( z ) соответственно. Заметим, что данные функции принято называть [1] вертикальными собственными функциями волновода. Данные системы функций являются полными и ортогональными в функциональных пространствах L 2 [0; h j ] ( j =0, 1).

Тогда, пользуясь полнотой системы функций { ф₀ n ( z ; § ₀ n ) } ”= 0 , можно представить потенциал скорости Ф( r , z ) во внутренней области (0) в виде суммы нормальных мод:

от

Ф 0 ( r , z ) = £ Ф 0 n ( z ;§ 0 n ) ( A n J 0 (§ 0 пГ ) + B_nH 01) (§ 0 , r ) ) , (5) n = 0

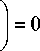
где A n , B n - произвольные постоянные.

После подстановки выражения (5) в неоднородное уравнение Гельмгольца (1) с учетом соотношения

т.е. поле любого излучателя в этом случае может быть записано в виде расходящейся волны с амплитудой, меняющей по закону 1/ r .

jL ₊ 1^ £2 !_Я(1- _{r) =} W) ^{+      +} § 0 n I H 0 ⁽§ 0 n r )

д r    r д r      J                2 n r

получим функциональное равенство:

i

E B n Ф о n ( ^z ; ^£ n ) =v^{8 ( z} - ^z o ).             (6)

n = 0                    ⁴

Используя далее ортогональность собственных функций {фоn (z; ^on)}^=о на отрезке [0; hо], можно найти, что iφ0n(z0; ξ0n)

B n = h .

⁴ j ф 0 n ⁽ s ; ^£ о n ) ds 0

Таким образом, условие в источнике звука выполнено, и потенциалы скорости звука можно записать следующим образом

. i ^ф0 n ^{( z} 0 )^ф0 n ^{( z} )_w(l)/e        V Л \ Г A

^Ф0 > ---------------- H 0 ) ( ^£0 n r ) ⁺ E A n Ф 0 n ( ^z ) J 0 ( ^£0 n r )

4 n=0        Y 0 nn при r < Г0,(7)

Ф1 = E CnФ1 n (z) H01) (£1nr) при r ^ r0 , n=0

где Y 0 n = C ⁰ Ф 2 n ⁽ s ) ds , ^£ 0 n , £ 1 n ^- горизонтальные соб^- 0

ственные числа, которые находятся из краевых задач (3) и (4). Подставляя выражения звуковых потенциалов в граничные условия и условия непрерывности

Ф 1 ( ^r 0 , ^z ) = Ф 0 ( ^r 0 , ^z ) , ^{z e} [ ⁰; ^h 0 ]

8 Ф 1 ( r 0 , z ) Hd r k z ) , z « [ 0; h 0 ]

----д------ I     d r                   ,          ⁽⁹⁾ r        [ 0,            z e ( h 0 ;^]

в силу ортогональности собственных функций φ j,n ( z ) соответствующих краевых задач в L 2 [0; h j ], строим бесконечную систему линейных алгебраических уравнений относительно неопределенных коэффициентов A n , C n :

“

A m = e см™ + B m ⁱ⁾, n = 0

от

C m = E AM^ + B^, n = 0

,        .    f nh (m +1/2) | ih (m +1/ 2) cos ------------

L h

4 m H 1 ⁽¹⁾ ( £ 1 mr> )

„ ( - 1 ) m H « ( £ 0 n r ,) sin f ^nZ0!^ j ■^E     h , ² ( n + 1/2 ) 2 - h ₀ ² ( m + 1/2 ) 2

Заметим, что для неоднородного профиля скорости звука c j ( z ) представленные выше формулы будут давать приближенные значения коэффициентов и свободных членов бесконечной системы при больших значениях индексов m , n в силу того, что вертикальные собственные функции асимптотически приближаются с ростом номера к соответствующим вертикальным собственным функциям sin nz ( n + 1/2 ) / h j для постоянного профиля скорости звука. Можно показать, что представленная выше бесконечная система удовлетворяет условиям квазирегулярности для постоянного профиля скорости звука, данные оценки с точностью до бесконечно малых будут соответствовать и неоднородному случаю.

Рассмотрим волновод с впадиной, данный рельеф дна можно встретить в любом районе Мирового океана. На рис. 2 изображен гидроакустический волновод, имеющий впадину с радиальной симметрией, внутри которого расположен точечный гармонический источник звука. Разобьем волновод на три области, определяемые скоростью звука c j ( z ) и постоянной глубиной h j ( j' = 0, 1, 2), плотность жидкости р полагаем постоянной во всех областях. Распространение звуковых волн описывается неоднородным уравнением Гельмгольца (1).

r 0        r 1

z 0

h 2

h 0 h 1

Рис. 2. Волновод с впадиной

Fig.2. Waveguide with cavity

z где

(1)     2 h 0 h 1

1 mn

m(          f ⁿ h ( ^{n + 1/2}Л

-1 [П + 1/2 cos h01) (£1 nr)) L h J

J 0 ( £ 0 m r )      h ² ( m + 1/2 ) ² - h ₀ ² ( n + 1/2 ) 2

Полагаем, что поверхность волновода является акустически мягкой, а дно – акустически жестким:

Ф( r ,0) = 0;

дФ д n L

= 0,

M

mn

2 h 0 ² ξ 0 n πξ _{1 m}

^J 1 ( ^£ 0 n r 0 ) •

H ( £ 1 m r )

( mt            ^{f П} h 0 ( m ^{+ 1/2} ) ^

(-1) (m +1/2) cos I -h-^   I h (n +1/2)2 -h02 (m +1/2)2

B ⁽¹⁾ = m

i ^H 0 ¹ ’ ( ^£ 0 m ^r 0 ) - ^{f nZ} 0 ( m ^{+ 1/2} ) • Sin I

^{2 J} 0 ^{( £} 0 m ^r 0 )       L       ^h 0

где L – кривая, определяющая форму дна.

Решение для волновода с впадиной, удовлетворяющее как граничным условиям на горизонтальных стенках волновода, так и условию излучения, снова строится в виде суммы нормальных мод.

Общее решение для данной краевой задачи имеет следующий вид:

Ф = . j V .n fz.^z) H <„ ₍ £ 0 _ r ^j А .ф _ n (z) J 0 _fe n r ) . ⁴ n = 0        ^Y0 n                         n = 0

от                                            от

Ф 1 = E 4Ф 1 n ^{( z} ) J о ( ^ i n r ) + E ^П ф х n ^{( z} ) ^H 0 ¹ ’ ( ^£ 1 n r ) ;

n = 0                              n = 0

от

Ф 2 = E B n 4 n ( z ) H 01 ( £ 2 n r ) , n = 0

hj где Yjn = J (фjn (s))2 ds , £jn, Ф^ (z) - собственные числа 0

и собственные функции соответствующих краевых задач.

Из условий непрерывности звукового поля на границах раздела частичных областей r = r k ( k = 0, 1):

Г Ф 0 ( R 0 , z ),   z е [0; h 0].

Ы R 0 , z ),   z е ( h 0 ; h i ];

д Ф 1     _Z1-)t⁽ R 0 ’ z )’

—⁽ R 0 ’ ^z ) = ) 5 r

5 r             I 0, z е [0;h0)

z е [ h 0 . h 1 ]

Г Ф, ( R, , z ), z е [0; h , ]

Ф,( R , z ) =                         ^2J

¹        >1 ( R 1 , z ), z е ( h 2 ; h 1 ]^;

д Ф^я 1 lv⁽ R 1 , z ), z е [0; h 2 )

-z—^{( R} 1 , ^z ) = S 5 r

⁵ r             | 0,          z е [ h 2 ; h 1 ]

Энергетические характеристики волновода

Согласно [26; 27] средней поток мощности волны в областях декомпозиции волновода вычисляется следующим образом:

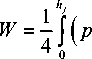
vr + pv*) dz, где p = -iюрФ - звуковое давление, v - колебательная скорость vr = Ф‘, vz = Oz * - знак комплексного сопря жения.

Подставляя выражения (2) и проводя соответствующие преобразования, получим формулы для среднего потока мощности сквозь зону стыка областей (0) и (1) волновода. Тогда средний поток мощности от источника в области над выступом (0) через сечение r = r0 выражается как сумма средних потоков мощности каждой из нормальных мод w _ Ю у Ф0n (z0)£0n

" = ^E

² n =0       ⁴

x(( J1 ( £0 nr0 ) *0 ( £0 nr0 )-J 0 ( £0 nr0 ) Y ( £0 nr0 ))f ^n’z0) + Im An Y ^ 4Y0 n          J ю -ОТ

⁺ У E Ф 0 n ^{( z} 0 )! ^£ 0 n l^{Im A} n ( ^K 0 ( I ^£ 0 n I ^r 0 ) 1 1 ( I ^£ 0 n I ^r 0 ) ⁺

⁴ⁿ n = N 0 +1

+ K1 (I £0nlr) 10 (I £0nlr))’ получаем бесконечную систему линейных алгебраических уравнений относительно неопределенных коэффициентов {An} и {Bj} в представлении амплитуды потенциала скоростей:

1 m

от

^{1 1} -У 1 ¹ m / t m ,?

от

от

, n^xn

-У 1 ² y ¹ -У I- / <  m , n-yn / , m

^Y1 m ^£1 m

n = 0

от

,2 J 0 (^ 1 n r ,) x 1 = Q 1.

m , n t \ ^xn Q m ^; J 0^(£1 n^r 1 )

^Y1 m ^ 1 m

¹ m ^{+ Y}1 m S 1 m

от

E l 4 1 .

I m , n x n ⁺ Y 1 m

’At

H iA^ m r ⁰ ) y ¹ -y 1 ¹_£, и (1) ft ^\^{- E m} ’ ⁿ ’ H 0 ⁽ S 1 m^r 0 ) n = 0

H ^ 1

и i¹)..A m  ^E ■

H 0 ^{( £}1 m^r0 ) n = 0

от

. ^J 1 ⁽ ^ 0 n r 0 ) 0=^2. ⁽¹¹⁾ ’ 0 n r (r xnn Qm ^;

(1)                          _от

H 0 (^£ 1 n^r1 ) 1 _ у .3 2 _ Q. tt (1)/t \ yn ^E I m , n y n = ^0;

H 0 ^{( £}1 n^r 0 )       n = 0

(1)                           от                      (1)

. ¹¹ 1 ^(£1 m^r1 ) 1 _y A ¹¹ 1 ^(£2 n^r1 ) 2 _ «

’ 1 m rj(1) / t \ y m   ^E I m , n ^£2 n r_r(1) / - \ y n = ’

H 0 ^{( £}1 m^r 0 )        n = 0           H 0 ^{( £}2 n r 1 )

где N j +1 - число распространяющихся нормальных волн области над выступом, I _v ( z ) , K _v ( z ) - модифицированные функции Бесселя первого и второго рода [28].

Средний поток мощности области без выступа (1), подводимый через сечение r = r ₀, представляет собой сумму средних потоков мощности распространяющихся нормальных волн:

n ¹

W 1) = 7 Ei c n I² Y 1 n £ 1 n ( j 1 ( £ 1 n r ) y ( £ 1 n r ) -

² n = 0

- J 0 ( £ 1 n r ) Y 1 ( £ 1 Л ) ) ,

m = 0,1, 2...

где xn, = A0 J0^0 Л); xn = An J0(^1 nr);

У n = B n H 0¹U Л); y n = B n H 0^1 n r 1 );

C = J Ф 0 n Ф 1 m dz ; Q m = i E '^? ’ z ' I mn H 0 ¹ ( £0_Л ) ;

0                      ⁴ n = 0    ^Y 0 n

I mn = J Ф 1 n Ф 1 m dz ; Q m = i E ^{ф 1} z ¹ I m ’ n £ 0 n H 1’ ¹ ( £0 _Л ) ;

h0                        4 n=0 Y0n h 2                          h

I mn = J Ф 2 n Ф 1 m ^dz ; I m , n = J Ф 1 n Ф 1 m ^dz

0                              h ₂

где N 1 + 1 - число распространяющихся нормальных волн области без выступа.

Согласно закону сохранения энергии следует равенство:

w

W (1) = ₁

w ’

W (0)

которое может служить критерием точности решения бесконечной системы линейных алгебраических уравнений.

Также можно вычислить [29] еще одну важную характеристику - среднюю «перекрестную» энергию, приходящуюся на единицу длины волновода нормальной волны и ее сопряженной

1 j **

E =J( vrvr * + vzvZ ) dz, 40

используя аналитическую форму представленного решения, получаем

N 0

( vr )o = £ Ф0n ( z ) §0n n=0

+ i

Ю

+ £ Фоn (z)|§0n| n=N о +1

Re A n J 1 ( § o n r ) -

Ф о n ( ^z o ) 4γ_{0 n}

+

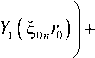
W 0 = 7 £ ^Ф0 n ⁽ z ⁰⁾ § ⁰ n ( J 1 (§ 0 n r 0 ) Y 0 (§ 0 n r , ) - J 0 (§ 0 n r , ) Y (§ 0 n r ) ) x ^- n = 0      ⁴

x' Фс п Ы + Im A_n ’ 1 +

I 4Y 0 n          n J

⁺г £ Ф 0 n ( z 0 ) i§ 0 n i Im A n ^x

⁴ⁿ n = N 0 + 1

x ( K 0 ( § 0 >0 ) 1 1(1 § 0 >0 ) + K 1(| § 0 >0 ) 1 0(| § 0 >0 ) ) ,

Ф о n ( ^z 0 )

2πγ_{0 n}

K i (| § 0 n\ r ) — Re A n I i (| § 0 n l r )

- i Im A n I i (I § 0 n| r 0 ) ] ;

где N 0 + 1 – число распространяющихся нормальных волн области над впадиной.

Средний поток мощности области с впадиной, подводимый через сечения r = r i , ( i = 0,1) есть сумма средних потоков мощности распространяющихся нормальных волн:

N 1

( vr )1 = £ Ф1 n ( z )§1 n [( Re CnJ1 ( §1 nr0 ) — Im CnY0 ( §1 nr0 )) + n=0

+ i ( Re C n Y 1 ( § 1 n r 0 ) + Im C J 1 ( § 1 „ Г 0 ) ) ] +

+ - £ Ф 1 n ( z )|§ 1 n |[ Im CK 1 (| § 1 >0 ) — i Re CK 1 (| § 1 n| r ) ]

^П n = N 1 + 1

N 1

W 1i = - £ Y 1 n § 1 n ( Y 0 (§ 1 n r ) J 1 (§ 1 n r ) - Y (§ 1 n r) J 0 (§ 1 n r) ) x ^— n = 0

x ( B ‘I² + Re B 1 Re A ' + Im B ' Im A *) + nnnnn

+ - £ Y 1 n |§ 1 n | ( K 0 (§ 1 n| r ) 1 1 (§ 1 n| r ) + K 1 (§ 1 n| r ) 1 0 (§ 1 n| r ) ) x

^П n = N 1 + 1

x( Re B ‘ Re A ‘ + Im B ‘ Im A ') , nn nn ^,

N 0

⁽ v z ) 0 = £ ф 0 n ⁽ z )

n = 0

Ф 0 n ( ^z 0 ) 4γ _{0 n}

Y 0 ( § 0 n r ) - Re A n J 0 ( § 0 n r )

— i ' ^ф 0 п ^{( z 0} ) J 0 ( § 0 n ^r 0 ) + Im A n J 0 ( § 0 n ^r 0 ^ 4^Y 0 n                                J

»

- £ Ф 0 n ( z )

n = N 0 + 1

[ Ф 0 n ( ^z 0 )

I ^-nY 0 n

^K 0 (| § 0 n|^r 0 ) ^{+ Re} A n ¹ 0 (| § 0 n|^r 0 ) l ⁺

⁺ i ^Im A n ¹ 0 (I § 0 n l ^r 0 ) ] ;

N 1

( v z ) 1 = £ Ф 1 ' n ( ^z ) ^[( ^{Im C} n ^Y 0 ( § 1 n ^r 0 ) — ^{Re C} n ^J 0 ( § 1 n ^r 0 ) )^- n = 0

— i ( Re C n Y 0 ( § 1 n r ) + Im C n J 0 ( § 1 n r ) ) ]-

- £ ф 0 n ⁽ z n = N 1 + 1

) -Im CK 0 (| § 1 n| r ) - i -Re C n K 0 (| § 1 n| r 0 ) •

где N 1 + 1 – число распространяющихся нормальных волн области с впадиной.

Аналогично находится средний поток мощности области, подводимый через сечение r = r 1 :

N 2       2

W - = 7 £ B -| Y - n § 2 n ( J 1 (§ 2 п Г ‘ ) Y >(§ 2 п Г ‘ ) - J 0 (§ 2 n r ‘ ) Y (§ 2 n r) ) ,

² n = 0

где N 2 + 1 – число распространяющихся нормальных волн данной области.

Зная средние потоки мощности в различных областях волновода, можно найти энергетические уровни

L 1 = 101g

W 0

' W 1

, ^L 2 = ¹⁰lg [ W J .

Согласно закону сохранения энергии на стыке областей декомпозиции следует равенство:

L 1 = L ₂ .

Далее, зная средние «перекрестные» энергии, можно, согласно [30], вычислить энергетический уровень

L = 101g

' E -1)

₄ E (0)

.

Полученное аналитическое решение позволяет также исследовать энергетические характеристики распространения звука проникновения звуковой волны сквозь области скачкообразного изменения сечения волновода с впадиной. Средний поток мощности от источника в области через сечение r = r 0 есть сумма средних потоков мощности каждой из нормальных мод

Численные результаты

Представленная выше теория позволяет найти решение для ступенчатого морского акустического волновода в виде суммы нормальных мод. При этом коэффициенты при модах определяются из решения бесконечных систем (10) и (11). Для численного решения бесконечных систем использовался метод простой редукции, когда неизвестные и уравнения с номерами, большими некоторого N, отбрасывались. Численный анализ показывает, что неизвестные с номерами, меньшими [N/2], сходятся к искомому решению бесконечной системы с ростом N. Неизвестные с номерами, заключенными на интервале [N/2; N], несут в себе погрешность, связанную с методом простой редукции. Подобное явление наблюдается и при использовании метода редукции для регулярных бесконечных систем линейных алгебраических уравнений, а именно значения первых неизвестных из редуцированной системы всегда дают более точное приближение к искомому решению бесконечной системы, чем последние [24].

Полученные формулы позволяют провести расчеты потоков энергии в сечении волновода r = r 0 для каждой из областей декомпозиции волновода, что дает возможность исследовать трансформацию звуковой волны сквозь неоднородность волновода. В табл. 1 приведены значения среднего потока мощности W (0) через зону стыка областей (0) и (1) при разных значениях отношения характерных размеров в областях декомпозиции волновода h 0 / h 1 (скачкообразное расширение волновода) и положения источника z 0 .

Из данных табл. 1 видно, что значения среднего потока мощности W (0) существенно зависят от относительной высоты подводного выступа h 0 / h 1 и положения источника z 0 . Можно увидеть, что с погружением источника в целом возрастает средний поток мощности через скачок сечения волновода, при этом погружение источника звука с z 0 = 0,1 h 1 до z 0 = 0,2 h 1 приводит к увеличению среднего потока мощности W (0) в среднем в 3,5 раза для выступа любой высоты. Интересен также тот факт, что резкий спад W (0) наблюдается, когда h 0 = 0,7 h 1 для всех значений z 0 , в то же время при h 0 = 0,8 h 1 и h 0 = 0,9 h 1 имеется возрастание величины W (0) . При высоте выступа h 0 = = 0,4 h 1 , наоборот, имеется ярко выраженный максимум для любого представленного расположения источника.

В табл. 2 приведены значения энергетического уровня L через зону стыка областей (0) и (1) при разных значениях отношения характерных размеров в областях декомпозиции волновода h 0 / h 1 (скачкообразное расширение волновода) и частоты ω .

Таблица 1

Зависимость среднего потока мощности W (0) через сечение r = r 0 от высоты выступа h 0 / h 1 и положения источника z 0 для следующих параметров волновода h 1 = 100 м, r 0 = 2 h 1 , c = 1460 м/с, ω = 100 рад/с

Table 1

Dependence of the average power flux W (0) through the section r = r 0 on the protrusion height h 0 / h 1 and the source position z 0 for the following waveguide parameters h 1 = 100 m, r 0 = 2 h 1 , c = 1460 m/s, ω = 100 rad/s

z 0 = 0.1 h 1

h 0 / h 1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9
W (0)	0,000466	0,000063	0,000138	0,000033	0,000020	0,000008	0,000057	0,000061

z 0 = 0.2 h 1

h 0 / h 1	-	0,3	0,4	0,5	0,6	0,7	0,8	0,9
W (0)	-	0,000191	0,000473	0,000121	0,000074	0,000024	0,000174	0,000184

z 0 = 0.3 h 1

h 0 / h 1	-	-	0,4	0,5	0,6	0,7	0,8	0,9
W (0)	-	-	0,000813	0,000230	0,000149	0,000044	0,000248	0,000254

Таблица 2

Зависимость энергетического уровня L в сечении r = r 0 от высоты выступа h 0 / h 1 и частоты ω для следующих параметров волновода h 1 = 100 м, r 0 = 2 h 1 , c = 1460 м/с, z 0 = 0,1 h 1

Table 2

Dependence of the energy level L for the section r = r 0 on the protrusion height h 0 / h 1 and frequency ω for the following waveguide parameters h 1 = 100 m, r 0 = 2 h 1 , c = 1460 m/s, z 0 = 0.1 h 1

ω = 50 рад/с

h 0 / h 1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9
L	0,667954	1,015026	1,351402	1,556649	1,544030	1,304603	0,899177	0,377024

ω = 100 рад/с

h 0 / h 1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9
L	1,522634	2,093684	1,983074	1,569850	1,127358	1,488416	0,594496	0,514390

ω =200 рад/с

h 0 / h 1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9
L	3,175774	1,518363	2,598074	1,030743	1,746812	1,847459	0,742270	1,547922

Данные табл. 2 показывают, что зависимость энергетического уровня L от относительной высоты выступа имеет сложный характер, существенно зависящий от частоты. Очевидно, что с ростом частоты в целом растут значения и энергетического уровня, тем не менее эта зависимость представляет собой осциллирующую функцию, которая имеет один максимум для ω = 50 рад/с, два для ω = 100 рад/с и три максимума для ω = 200 рад/с. Из данных табл. 2 можно заметить резкий спад энергетического уровня L в сечении r = r 0 при h 0 =80 м для всех приведенных частот ω и при h 0 = 90 м для ω = 50 рад/с и ω = 200 рад/с, что связано с относительно небольшим размером выступа по высоте.

Как известно [8; 24; 30], изменение амплитуды поля в волноводе характеризуется величиной потерь при распространении (интенсивность):

TL = - 20lg

Φ ^w* Φ

где

Qe ikr Φ=

4 π r

– амплитуда потенциала скоростей, созда- ваемая точечным источником звука на расстоянии r = 1 м в безграничной среде; Q – объемная колебательная скорость. В табл. 3 приведены значения энергетического уровня L и величины потерь TL(z0) через зону стыка областей (0) и (1) при разных значениях отношения h0/h1.

Таблица 3

Сравнение энергетического уровня L и величины потерь TL ( z 0 ) для r = r 0 в зависимости от высоты выступа h 0 / h 1 при h 1 = 100 м, r 0 = 2 h 1 , c = 1460 м/с, z 0 = 0,1 h 1 , ω = 100 рад/с

Table 3

Comparison of energy level L and loss value TL ( z 0 ) for the section r = r 0 on the protrusion height h 0 / h 1 for the following waveguide parameters h 1 = 100 m, r 0 = 2 h 1 , c = 1460 m/s, z 0 = 0,1 h 1 , ω = 100 rad/s

h 0 / h 1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9
L	1,522634	2,093684	1,983074	1,569850	1,127358	1,488416	0,594496	0,514390
TL	–91,5919	–39,9224	–41,7737	–50,9208	–53,8741	–44,9289	–45,3429	–46,9909

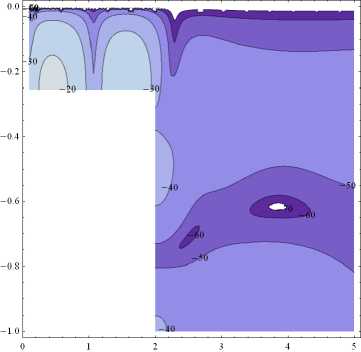
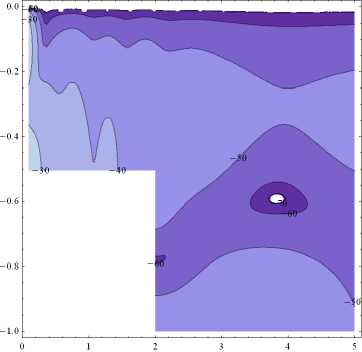
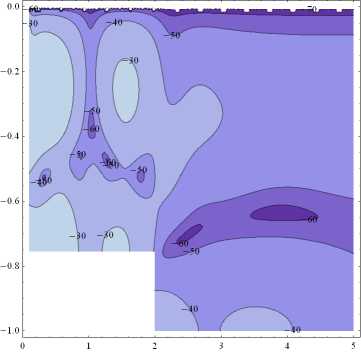
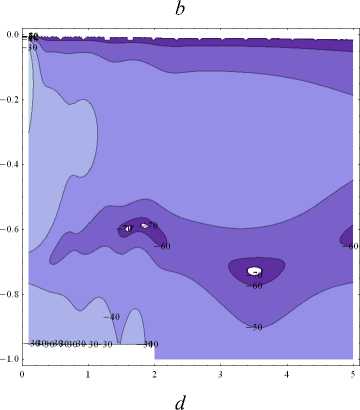
Рис. 3. Величина потерь в зависимости от высоты выступа ( а–d ) – h 0 = 0,25 h 1 , h 0 = 0,5 h 1 , h 0 = 0,75 h 1 , h 0 = 0,95 h 1 при h 1 = 100 м, r 0 = 2 h 1 , c = 1460 м/с, z 0 = 0,1 h 1 , ω = 100 рад/с

Fig. 3. Loss value on the protrusion height for the following waveguide parameters ( а–d ) – h 0 = 0.25 h 1 , h 0 = 0.5 h 1 , h 0 = 0.75 h 1 , h 0 = 0.95 h 1 when h 1 = 100 m, r 0 = 2 h 1 , c = 1460 m/s, z 0 = 0.1 h 1 , ω =100 rad/s

Из данных табл. 3 видно, при возрастании энергетического уровня L наблюдается уменьшение величины TL ( z 0 ) до тех пор, пока величина выступа не оказывается малой в сравнении с глубиной волновода ( h 0 < 0,7 h 1 ), где величина потерь оказывается практически неизменной.

Для наглядной оценки влияния выступа на величину потерь TL ( z 0 ) представлен рис. 3.

На рис. 3 заметны качественные изменения величины потерь TL ( z 0 ) в зависимости от высоты выступа в областях (0) и (1).

Заметим, что на всех рисунках имеется область повышенных потерь TL при r « 2 r ₀ , z « 0,6 h 1 .

Заключение

Таким образом, в статье получено численно-аналитическое решение задачи о звуковом поле в волноводе с подводным выступом и впадиной цилиндрической формы, которое позволяет исследовать различные эффекты, связанные с формой дна, в частности, энергетические характеристики. Приведенные результаты представляют сведения о влиянии неровностей дна с радиальной симметрией на процесс распространения волн в волноводе. Они позволяют для каждого конкретного случая рассчитать, является ли влияние формы неровностей дна существенным или в какой мере этим влиянием можно пренебречь.