Энергетические характеристики взаимодействия точечных дефектов с симметрично-наклонной границей 5(210)[001] в сплаве FeCr

Межзеренные границы (ГЗ) традиционно рассматриваются как стоки для точечных дефектов и примесных атомов. Однако, детальные исследования механизмов взаимодействия ГЗ с указанными дефектами на атомарном уровне начали проводиться сравнительно недавно. Знание структуры и энергетических характеристик межзеренных границ (ГЗ – граница зерна) важно для понимания таких явлений, происходящих в материалах, как рост зерен, зернограничная диффузия, сегрегация примесей, деформация и разрушение (см. работу [1] и дальнейшие ссылки в ней).

В работе [1] Zhang et al., используя многочастичный потенциал межатомного взаимодействия на основе модифицированного аналитического метода погруженного атома [2], рассчитали удельные энергии для 27 различных симметрично наклонных ГЗ в a -Fe. Однако их оценки оказались несколько завышенными по сравнению с более поздними исследованиями (см., например, Тихончев Михаил Юрьевич, кандидат физико-математических наук, начальник лаборатории моделирования поведения неорганических материалов.

работы [6,8,9]). В 1999-2001 годах Perez and Smith [3, 7] на основе потенциала Финниса-Синклера одними из первых провели молекулярно-динамическое (МД) моделирование каскадов атомных смещений возле СНГЗ в чистом железе. Была установлена склонность произведенных в каскаде точечных дефектов (вакансий и СМА – собственных междоузедльных атомов) аккумулироваться в тонком слое, прилегающем к ГЗ. Аналогичный вывод был сделан и в недавней работе [21]. Martino et al. [4] провели МД-моделирование каскадов атомных смещений возле симметрично наклонных ГЗ в железе, содержащем примесный фосфор. Моделирование проведено на основе многочастичного межатомного взаимодействия для энергий первично-выбитого атома (ПВА) 0.5 – 6 кэВ в интервале температур 400 – 700 °С. Было установлено, что ГЗ является барьером на пути движения и рекомбинации точечных дефектов, которые скапливаются и сохраняют стабильность вблизи ГЗ. Отмечено тенденция к миграции междоузельного фосфора в направлении к ГЗ. В работе [5] методом МД исследовалась диффузия одиночной вакансии в приграничной зоне ГЗ в a -Fe. В работе [11] Terentyev et al. применили метод Монте-Карло для исследования сегрегации Cr в сплавах Fe-xCr, x=5, 10, 14 ат. % в температурном интервале 300 – 900 К. В работе [12] проведено расчетное исследование особенностей прохождения каскадов через границу раздела фаз ГПУ Zr и ОЦК Nb и пороговых энергий смещения в межфазной области.

Настоящая работа посвящена исследованию ряда энергетических свойств симметрично наклонной ГЗ 2 5(210)[001] в a -Fe и сплаве Fe-9ат.%Cr. Исследование проводится путем моделирования методом молекулярной динамики. Выбор сплава обусловлен тем, что высо-кохромистые феррито-мартенситные сплавы рассматриваются в качестве кандидатных материалов первой стенки и элементов бланкета будущих реакторов синтеза [13-15].

• 2.    МЕТОД МОДЕЛИРОВАНИЯ

Симметрично наклонная или двойниковая ГЗ представляет собой плоскость зеркальной симметрии между двумя монокристаллами и считается наиболее простым типом ГЗ. Такие ГЗ нарушают трансляционную инвариантность в направлении, перпендикулярном ее плоскости. В направлениях параллельных границе трансляционная симметрия сохраняется (рис. 1). В настоящем исследовании мы ограничились рассмотрением одного типа симметрично наклонных ГЗ для ОЦК структуры: 2 5(210) с осью вращения [001]. Модельный бикристаллит строили так, чтобы ось Z была коллинеарна оси вращения монокристаллов, ось X – нормаль к СНГЗ, ось Y – третья ось декартовой системы координат. На граничных плоскостях перпендикулярных ГЗ использовали периодические граничные условия. Координаты атомов, попадающих в слои шириной ~ 0.6 нм, прилегающие к границам параллельным ГЗ, фиксировали после построения бикристаллита и не меняли в ходе дальнейших расчетов. Т.о. на граничных плоскостях параллельных ГЗ использовались жесткие граничные условия (см. рис. 2).

Рассматривали два типа кристаллита: чистое железо и случайный бинарный сплав Fe-9ат.%Cr. Для железа использовали многочастичный потенциал из работы [16]. Для описания межатомного взаимодействия в системе FeCr ис- пользовали модифицированную версию многочастичного потенциала, предложенного А. Каро и др. [17]. Описание модифицированной версии этого потенциала можно найти в нашей работе [18]. Параметры модельных бикристаллитов представлены ниже в табл. 1.

После построения составного бикристалла методом молекулярной статики проводили релаксацию системы при нулевой температуре. При необходимости изменения температуры или состава размер релаксированного бикристаллита изменялся в соответствие с параметром решетки (a0), который обеспечивает используемый потенциал в идеальном монокристалле такого же состава и температуры. Измененный бикристаллит релаксировали методом молекулярной динамики с использованием термостата Берендсена в течении 10 пс.

Удельную энергию границы рассчитывали по формуле

Y gb = ( E gb - E c • n )/ S' , (1) где E_GB – энергия модельного бикристаллита, E_c – энергия связи идеального кристалла на один атом, n – число атомов в системе, S – площадь ГЗ в модельном бикристаллите.

В ходе релаксации бикристаллита атомы в нескольких атомных слоях, прилегающих с обеих сторон к ГЗ, заметно смещаются из узлов кристаллических решеток. Эти атомные слои образуют зернограничную область. Размер зернограничной области определялся методом, основанном на анализе потенциальной энергии кристаллита в прилегающих к ГЗ областях (см., например, работу [10]). В этом методе исследуемый бикристаллит разбивается, начиная от ГЗ, на тонкие слои параллельные плоскости распространения ГЗ. В каждом таком слое вычисляется значение потенциальной энергии E_p , приходящееся на один атом. Слои не содержащие атомов игнорируются. Граница зернограничной области определяется как плоскости посередине между двумя слоями, в ко-

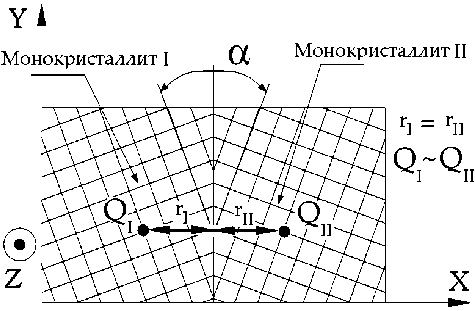
Рис. 1. Схематичное изображение симметрично наклонной границы зерна

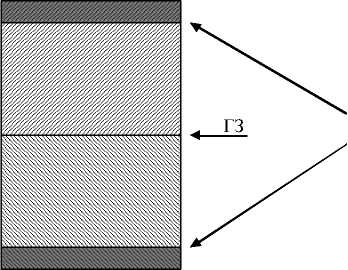
Фиксированные атомы

Рис. 2. Схема задания расчетной области с симметрично наклонной границы зерна

Таблица 1. Характеристики ГЗ.

T - температура, У GB - удельная энергия границы, w GB - ширина зернограничной области.

В скобках представлена оценка других исследователей.

Разм ер б икристалла , а о Х а о Х а о	Число ат омов	Чист ое Fe, T = 0K		Fe – 9ат.%Cr
				T = 0K		T = 300K
		Y GB , Дж/м2	w GB , Å	Y GB , Дж/м2	w GB , Å	Y GB , Дж/м2	w GB , Å
80.5 x 58.1 x 59.0	550706	1.12 (1.39[19])	13.8	1.18 ± 0.02*	11.9 ± 1.3	1.11 ± 0.04	11.7 ± 1.2

* Здесь и далее погрешности носят статистический характер и определяются как одно стандартное отклонение (1 Г ) для выборочного среднего

торых отклонение E_p от E_c соответственно превышает и не превышает заданной величины A E . В данной работе мы рассматривали слои шириной 0.2 Л и A E = 0.01 эВ.

• 3.    РЕЗУЛЬТАТЫ

Оценки удельных энергий рассматриваемой ГЗ и размера зернограничной области представлены в табл. 1. В табл.1 также приводятся оценки удельной энергии ГЗ в чистом железе, полученные ранее другими исследователями. Несмотря на имеющиеся отличия, в целом наблюдается удовлетворительное согласие наших расчетов с результатами других исследователей. Согласно полученным результатам происходит небольшое (на 0.06 Дж/м2) повышение энергии ГЗ при переходе от чистого железа к сплаву Fe-9ат.%Cr. С повышением температуры до 300 К удельная энергия ГЗ снижается на 0.07 Дж/м2. Ширина зернограничной области составляет ~ 1 нм, слабо меняется с изменением состава и практически не меняется с ростом температуры системы от 0 до 300 К.

Для практически важных приложений связанных с изучением радиационной повреждаемости представляют интерес энергии формирования точечных дефектов (вакансии и СМА) и энергии замещения атомов матрицы примесными атомами, а также энергии связи дефектов с зернограничной областью.

В настоящем исследовании рассчитаны энергии связи с зернограничной областью вакансии, СМА, и Cr как атома замещения. Все оценки проведены в матрице чистого Fe при нулевой температуре. Наиболее энергетическая выгодная собственная междоузельная конфигурация в железе и хроме имеет вид гантели с ориентацией <110> (см., например, работы [16, 20] и дальнейшие ссылки в них). Поэтому здесь рассматриваются только гантельные конфигурации с ориентацией <110> двух типов: Fe-Fe и Fe-Cr. Энергия связи рассчитывалась как разность

^EGb = ^Ef k - E G»      <²>

f bulk

энергий формирования вдали от ГЗ ( E

) и

вблизи ГЗ ( E_G^f_B ). Энергии формирования вакансии и СМА рассчитывали по формуле

E GB = E GB ^- E GB ^{+ к} "  E c ’ ⁽³⁾ где E_G^d_B – энергия реласксированного бикристаллита с точечным дефектом (вакансия или СМА), E_GB – энергия реласксированного бикристаллита без точечных дефектов,

( +1, для вакансии к =[ -1, для СМА ’

E_c – энергия связи на один атом идеального кристалла Fe ( E_c^Fe ) для случая вакансии или СМА

Cr типа Fe-Fe либо Cr (Ec ) для СМА смешанного типа Fe-Cr. Вблизи ГЗ энергия формирования СМА зависит от его ориентации относительно границы. Мы рассматривали все неэквивалентные ориентации и в качестве искомой энергии выбирали наименьшее из полученных значений.

Энергию замещения вычисляли по формуле subst Fe Cr

E Cr = E Fe + 1Cr ^- E Fe ⁺ E c ^- E c , ⁽⁴⁾ где E_Fe+1Cr – энергия кристаллита железа с одним атомом замещения хрома, E_Fe – энергия кристаллита железа содержащего такое же количество атомов.

Для используемого потенциала значения E_c составляют -4.013 эВ/атом для Fe [16] и -3,837 эВ/атом для Cr [20]. В монокристалле Fe релаксированная энергия формирования вакансии равна 1,72 эВ [16], энергии формирования СМА с ориентацией <110> составляют 3.51 и 3.31 эВ для гантелей Fe-Fe и Fe-Cr соответственно [18], энергия замещения одного атома железа атомом хрома равна -0.108 эВ [18].

Полученные энергии связи с зернограничной областью вакансии, СМА двух типов и атома замещения Cr представлены на рис. 3-6 соответственно.

Для полученных оценок наблюдаются скачкообразные изменения по мере удаления от ГЗ. Причем в случае вакансии и атома замещения эти скачки происходят со сменой знака. Из получен-

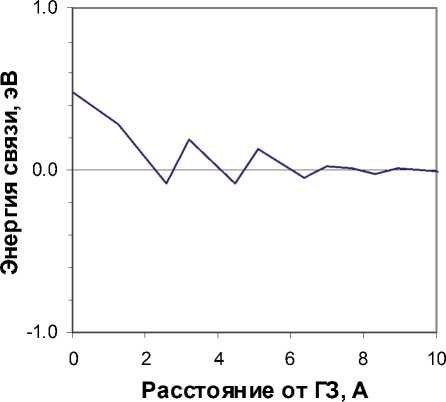
Рис. 3. Энергия связи вакансии с зернограничной областью в бикристаллите железа

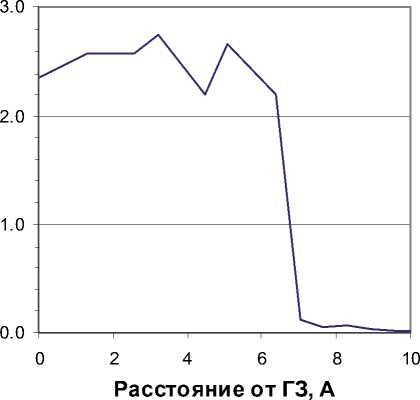
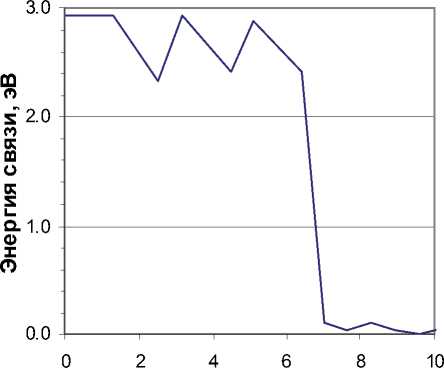
Рис. 5. Энергия связи СМА Fe-Cr<110> с зернограничной областью в бикристаллите железа ных результатов следует, что вакансия имеет положительную энергию связи с ГЗ. Максимальное значение энергии связи с межзеренной областью составляет 0.5 эВ. Наименьшие значения не опускаются ниже -0.08 эВ. СМА обоих типов имеют положительную энергию связи с межзеренной областью достигающую 2.9 эВ. При этом максимальное значение EGBB для гантелей Fe-Fe превосходит соответствующее значение для смешанных Fe-Cr СМА на 0.1 эВ.

• 4.    ЗАКЛЮЧЕНИЕ

В работе рассмотрена модель симметрично наклонной границы 2 5(210) с осью вращения [001] в железе и случайном сплаве Fe-9ат.%Cr. Моделирование проведено методом молекуляр-

Расстояние от ГЗ, A

Рис. 4. Энергия связи СМА Fe-Fe<110> с зернограничной областью в бикристаллите железа

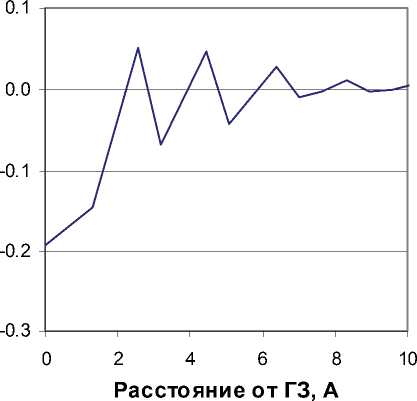
Рис. 6. Энергия связи атома замещения Cr с зернограничной областью в бикристаллите железа ной статики с использованием многочастичного межатомного взаимодействия. Получены оценки удельной энергии ГЗ и размера соответствующей зернограничной области. Для чистого железа при нулевой температуре отмечено удовлетворительное согласие результатов расчетов с результатами других исследователей. Установлено, что при переходе от чистого железа к сплаву Fe-9ат.%Cr происходит незначительное повышение удельной энергии ГЗ (на ~0.1 Дж/м²). С повышением температуры сплава до 300 К удельная энергия ГЗ незначительно снижается на ~0.1 Дж/м². Ширина зернограничной области составляет ~ 1 нм, слабо меняется с изменением состава и практически не меняется с ростом температуры системы.

Для бикристалла железа рассчитаны энергии связи с зернограничной областью вакансии, двух типов междоузельных конфигураций (гантель с ориентацией <110> из двух атомов железа и гантель смешанного Fe-Cr типа той же ориентации) и замещающего атома Cr. Отмечены скачкообразные изменения полученных оценок по мере удаления от ГЗ, вплоть до периодической смены знака в случае вакансии и атома замещения. Обнаружена высокая положительная связь (~3 эВ) СМА обеих конфигураций с зернограничными областями всех рассматриваемых типов. Присоединение к зернограничной области вакансии так же следует рассматривать как энергетически выгодное (энергия связи 0.5 эВ). Эти результаты обосновывают свойство зернограничной области аккумулировать точечные дефекты в процессе радиационного повреждения материала, отмеченное, в частности, в работах [3, 4, 7, 21]. При этом накопление междоузельных атомов происходит более интенсивно как по причине более высокой энергии связи, так и вследствие их высокой подвижности.

Согласно полученным результатам присоединение с зернограничной области замещающего атома хрома нельзя однозначно трактовать как энергетически выгодное или невыгодное. Это объясняется сменой знака энергии связи при рассмотрении различных позиций в зернограничной области. Чаще эта энергия все же отрицательна. Этот результат следует сопоставить с работой [11], где получены соответствующие оценки энергии связи для границ 2 19(331), 2 9(221), 2 3(111), 2 3(112), 2 11(113) и 2 9(114) с осью вращения [110], а расчет проведен с двух-полосным (two band) многочастичным эмпирическим потенциалом. Авторами этой работы установлена положительная энергия связи замещающего атома Cr со всеми рассмотренными границами. Однако и в этом случае наблюдаются отрицательные значения энергии связи для отдельных позиций вблизи ГЗ. Поэтому, учитывая различие в типах рассмотренных границ, можно признать качественное согласие наших результатов с результатами из ранее опубликованных работ.

Работа выполнена при поддержке Минобрнауки в рамках государственного задания на 20122014 гг.