Энергетические спектры с полупроводниковых сплавов

Когда концентрация примесей становится достаточно большой, меняется энергетический спектр и ширина запрещенной зоны кристалла. В сильнолегированных полупроводниках особую роль играет взаимодействие носителей заряда с примесными атомами. Поглощение света с частотой меньшей пороговой ет = Eg / h естественно связано с наличием хвоста плотности состояний в запрещенной зоне. Полная концентрация уровней на хвостах меняется от вещества к веществу и от образца к образцу и часто оказывается довольно большой до 1019-1020 см-3.

Одним из главных факторов, определяющих ширину энергетических щелей, является критическое значение концентрации энергетических состояний. Когда критическая концентрация N k равна плотности энергетических состояний N s =N k , область энергией с меньшей концентрацией, чем N k , Ns ( E ) < Nk определяет область запрещенных состояний. И на оборот, когда область энергией с большей концентрацией, чем N k , Ns ( e ) > Nk энергия разрешенных состояний. Условия Ns ( E ) = Nk определяет край запрещенной зоны, дно зоны проводимости E_c , и потолок валентной зоны E v . При таком подходе температурная зависимость запрещенной зоны определяется температурной зависимостью плотности состояний. С помощью математической модели спектра плотности состояний была анализирована температурная зависимость дискретных энергетических уровней в запрещенной зоне кремния.

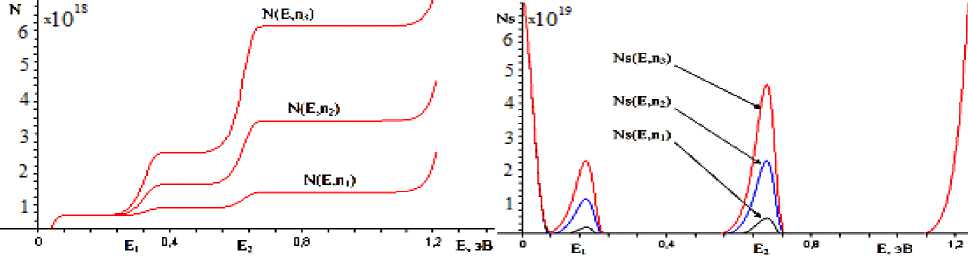
Рассмотрим эту модель для данной задачи. Если предположить, что коэффициенты поглощения пропорциональны плотности состояний комбинированная плотность состояний) то плотность состояний в бывшей запрещенной зоне на 10⁴ порядков ниже плотности состояний зоны проводимости и валентной зоны (10²²-10²⁰). В новой зоне в области значений Eg <0.9 Ns =10¹⁸-10¹⁹ (0.4< Eg <0.9 эВ ). Это значения плотности состояний дает коэффициенты поглощения а ~1-10 см^-2. Таким образом, с помощью легирования можно управлять шириной запрещенной зоны и коэффициентом поглощения.Используя вышеуказанную модель построим спектр плотности состояний для легированного кремния, учитывая экспериментальные условия, Т=300 К, Eg=1.21 э.В. Из рисунка видно, что большая концентрация примесей дает достаточно большое количество уровней определяемых кластерами, образованных примесными уровнями.

Уровни в запрещенной зоне создаются случайным распределением примесей. Коэффициент поглощения α пропорционален полному числу состояний. Возможно образование кластеров более подходит для объяснения коэффициента поглощения сильнолегированных полупроводников с глубокими уровнями. На рис.1. показан интегральная плотность состояний (полное число состояний) вычисленное по модели.Стоит отметить, что полученный график полного числа состояний с помощью модели рис.1. и экспериментальный график полного числа состояний сопоставимы. При достаточно большом количестве концентрации примесей дискретные уровни образуют примесьную зону. Учитывая это обстоятельство можно сделать вывод что, поглощения в интервале 0.5-0.9 эВ для кремния обусловлены примесными состояниями в запрещенной зоне(рис.2). Примесные состояния могут сильно уменьшать ширину запрещенной зоны полупроводника. Для исследования полупроводниковых сплавов построена модель температурной зависимости спектров плотности энергетических состояний учитывающий концентрационную долю содержимого сплава. Эту модель получили об используемой модели с прибавлением дополнительных условий. Формула (16) с учетом изменений получили следующий вид:

Ns ( E ) = Ns ^ ( E ) + Ns Ge ( E ) + Ns SS ( E ) + Ns ^e ( E ) + Ns S ( E ) + Ns ^e ( E ) (1)

Степень легирования n 1 23

Рисунок 1. Плотность состояний полученный по модели.

Степень легирования n 1 23

Рисунок 2. Полное число состояний, вычисленное по модели.

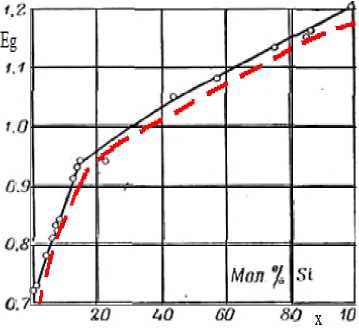
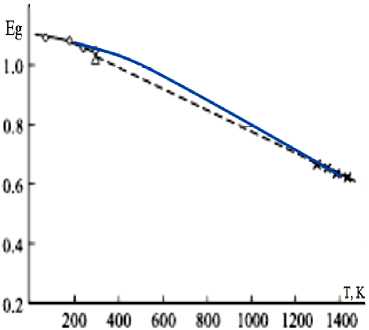
где: учитывая, что для E ^Si -энергия потолка валентной зоны для Si и E ^Ge -энергия потолка валентной зоны для Ge , в относительном энергетическом оси присваивается 0, E ^Si –ширина запрещенной зоны Si, E ^Ge –ширина запрещенной зоны Ge. E_i -может пробегать по всей валентной, запрещенной зоны и зоны проводимости. Ns -концентрация энергетических состояний соответству-ющая для энергии E_i , E- энергия состояний, Т- температура. k - постоянная Больцмана. С помощью модели исследуется спектр плотности состояний и концентрационная зависимость ширины запрещенной зоны для Si x Ge 1-x (Рис.3) и температурная зависимость ширины запрещенной зоны для

модель

Рисунок 3 Ширина запрещенной зоны от концентрации сплава для Si x Ge 1-x

--

-- эксперимент,

o ∆ x –эксперимент, ─ модель

Рисунок 4 Температурная зависимость ширины запрещенной зоны для Si 0.15 Ge 0.85

Si0.15Ge0.85  (Рис.4) со сравнением теоретических результатов с экспериментальными результатами. Сравнения теоретических и экспериментальных результатов приведены в рис. 3 и 4.

ЗАКЛЮЧЕНИЕ

На основе температурной зависимости термодинамической плотности энергетических состояний полупроводниковых материалов:

• 1.    Получена математическая модель, описывающая спектр температур-ной и концентрационной зависимости ширины запрещённой зоны энергетических состояний для полупроводникового сплава Si x Ge 1-x ,

• 2.    Получены по предложенной методике с помощью построенной математической модели спектры температурной зависимости ширины, запрещённой зоны полупроводникового сплава Si_xGe_1-x по всем 0≤x≤1.

позволяет определить спектр в широком температурном и энергетическом диапазоне;