Энергетический параметр высококачественной эффективной компрессии цифровых аудиоданных

Работа посвящена повышению качества компрессии цифровых аудиоданных. Рассматривается вопрос распределения бит при кодировании коэффициентов гармонических дискретных ортогональных преобразований, необходимых и достаточных для обеспечения высокого качества субъективного восприятия восстановленного звука. Приводятся рекомендации относительно этого распределения для различных рабочих полос звуковых сигналов.

Постановка задачи

В современных стандартизованных цифровых технологиях обработки и передачи звуковых сигналов (ЗС) используются дискретные косинусное преобразование (ДКП) и преобразование Фурье (ДПФ). При этом основное внимание уделяется энергетическому параметру сжатия – округлению (уменьшению разрядности кодирования) их коэффициентов. Известен [1] подход, позволяющий аналитически оценить допустимую степень округления модуля коэффициентов указанных преобразований. Однако соответствующий ме- тод дает равномерное ее распределение, что, как оказалось [2], в случае ДКП не обеспечивает высокого качества субъективного восприятия восстановленного звука, а в случае ДПФ является избыточным.

Авторы статьи предлагают метод оценки энергетического параметра сжатия, учитывающий фазовую компоненту коэффициентов ДКП и ДПФ, а также их частотные характеристики. В основу метода положены основные психоакустические свойства слуха.

Дискретное преобразование Фурье

В этом случае каждый k -й коэффициент С_k характеризуется модулем Y_k и фазой ϕ _k .

Хорошей интерпретацией процесса уменьшению разрядности кодирования Yk является [1] прямоугольная амплитудная модуляция полосного шума шириной Aрш k с центральной частотой f k = k - Af, где Af - разрешающая способность преобразования по частоте. Поскольку здесь Yk представляется величиной без знака, возможно только его усечение. Следовательно, согласно [1], допустимое число передаваемых старших разрядов модуля qY,k определяется выражением:

q y , k = Г log 2(1/m k) 1, (1)

где ⎡⎢ x ⎤⎥ – наименьшее целое, не меньшее x , m _k = m (1 / T _п ) + m (A F _m , _k ) — коэффициент минимально ощущаемой прямоугольной амплитудной модуляции полосного шума, а T_п – длительность интервала преобразования.

Зависимости m (1 / Т п ) и m (A F _{m k} ) определены эмпирически [3]. Известны [4] и оптимальные значения T_п для различного звукового материала. Остается выработать подход к оценке A Р ш _k .

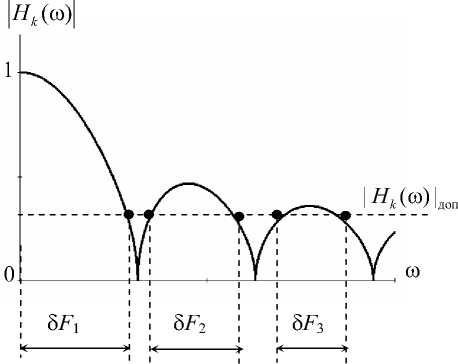
Рис. 1. Характер АЧХ C _k гармонических дискретных ортогональных преобразований

Прежде всего следует заметить, что согласно нормированной (| H _k ( го)| = |H(j ro)|/| H (j ro k )| , где ω – безразмерная частота) амплитудно-частотной характеристики (АЧХ) С_k (рис. 1) величина Y_k определяется суперпозицией множества спектральных компонент ЗС. Если пренебречь влиянием части из них на величину Y_k , новое значение модуля коэффициента преобразования будет отличаться от действительного его значения на величину Δ Y _k . Заметим также, что вследствие равновероятности знаков указанной части спектральных компонент влияние одной из них на величину Y_k частично или даже полностью компенсируется другими. Однако в наихудшем случае, который и представляет интерес, приращение Δ Y _k обусловливается только некоторой i -й спектральной компонентой S_i и по абсолютной величине составляет

A Y k = |H k ( и , )| • 10 D i ^/20 ,            (2)

где Di – верхняя граница динамического диапазона значений Si в пределах плоскости слышимости в децибелах. Но тогда в оценке ΔF можно пре-ш ,k небречь всеми спектральными компонентами ЗС, удовлетворяющими условию:

IH k ( « i)| <| H „ ( ^ ) доп ,             (3)

где |H _k ( to_: )| - максимально допустимое значение АЧХ, при котором влияние S_i на величину Y_k несущественно. На этом основании A F _{m k} будет определяться (см. рис. 1) как

АF _ш , k = £ 3 F i ,             (4)

i где i – номер лепестка АЧХ, для которого существует условие (3).

С другой стороны Δ Y _k определяет взаимодействие С_k с другими коэффициентами преобразования в смысле маскировки. Проявляется это в колебаниях среднего периода T _ОМ следования события отсутствия маскировки С_k , которое в свою очередь определяется соответствующей вероятностью P_k . С этой точки зрения Δ Y _k следует считать несущественным, если обусловленные им колебания T _ОМ не ощущаются на слух. Отсюда напрашивается вывод о существовании связи между |H _k ( to i )| и максимально допустимом изменении вероятности P_k .

С целью формализации этой связи рассмотрим некоторый большой интервал времени Т _Б>> Т _п. За это время будет передано n = Т _Б / T _п интервалов преобразования. С вероятностью P _k в n⋅ P _k из них С_k окажется немаскируемым. Средний интервал времени между такими событиями Т Ом = T Б /( n • P k ) = T n / P k .

Пусть теперь Y_k получил отрицательное приращение Δ Y _k , что соответствует наихудшему случаю. Действительно, при этом вероятность P_k уменьшится на величину

A P k = A Y k / Y k = |H k (ш i )| • 10 ⁽ D i ^- D ^{k )/20} ,   (5)

а T _ОМ увеличится на величину

A T om = T n /( P k —A P k ) - T n / P k .    (6)

Согласно условиям обработки цифровых аудиоданных в пределах T_п характер спектра не меняется. Следовательно, T_п яв л яется минимальным из в о зможных значений ΔT_ОМ . Потребуем, чтобы ΔT_ОМ не превышало этого значения. Отсюда с учетом (6) и (5) нетрудно получить условие оценки ΔF _k :

I H k ( ®i )|

P2

P _k

(1 + P k ) - 10 ⁽ D - D k ^)/20

= l^H k ⁽ ® i )l доп . (7)

Что касается ϕ k , она представляется знаковой величиной. Следовательно [5], возможно ее округление.

Округление ϕ _k означает уменьшение или увеличение f_k относительно своего номинального значения, причем это изменение может происходить только на стыках интервалов преобразования. Такой характер изменения можно интерпретировать как частотную модуляцию С_k с частотой модуляции f_m = 1/ Т_п .

Здесь следует заметить, что интерпретация С_k как тона не противоречит его предыдущей интерпретации. Действительно, согласно электроакустическим измерениям [6] для полосного шума совершенно безразличен характер распределения его интенсивности. Она может распределяться по всей его полосе или концентрироваться в одной лишь спектральной компоненте.

Пусть теперь модуль ϕ _k текущего интервала преобразования представлен q 1 _ϕ,k значащими разрядами. В результате округления q 2 _{ϕ ,k} младших разрядов обнуляются, вследствие чего достаточно передать только q^ = q^ _к - q 2 _ф , _t старших разрядов. При этом по правилам округления ϕ _k увеличится или уменьшится на величину, не превышающую Аф _k = 2 q ¹ ’ ^{- k - q} ’ ^{- k} /2 . Согласно принятой интерпретации округления ϕ _k относительному ее изменению Δϕ _k / ϕ _k можно сопоставить индекс модуляции δf _k / f _m , где δf _k – минимально ощущаемая на слух девиация частоты f_k . Тогда искажения, вызванные округлением ϕ k , не будут ощущаться на слух, если это отношение не превышает δf _k / f _m . Отсюда нетрудно получить выражение для оценки допустимого числа передаваемых старших разрядов модуля ϕ _k :

q _Ф , k = Г log 2 [i/( 5 f k • t „ )] - 1 1 . (8)

Относительно δf _k известны [3] экспериментальные зависимости 5 f ( f _k) , полученные при различных значениях f _m .. На их основе можно предложить следующую аппроксимацию функциональной зависимости § f ( f _k, f m ) :

3 f ( f k , f m ) = K 1( f m ) • 10 " ⁴ • f k ^/2 + ⁺ K 2( f m )/lg( f k ), ⁽⁾

где K 1( f_m ) и K 2( f_m ) определяются эмпирически.

Дискретное косинусное преобразование

Коэффициенты ДКП представляются знаковой величиной. Следовательно, рассуждая как в предыдущем случае, получаем:

q Y,k = [ ^log 2 (1/ m k ) ^- 1] ■ (10)

В данном преобразовании фаза в явном виде не определена. Однако это не означает отсутствие искажений, характерных для округления фазы.

В работе [3] представлены результаты экспериментальных исследований по восприятию слухом амплитудной и частотной модуляции. Оказалось, что слух различает эти виды модуляции лишь до некоторой граничной частоты несущего колебания. При более высоких частотах несущего колебания они ощущаются одинаково. На этом основании относительно коэффициентов ДКП представляется более правильным говорить о приоритетности интерпретаций округления как амплитудной и частотной модуляции. В связи с этим q_Y,k целесообразно определять следующим образом:

[q^,k, если q^,k > qy,k, q Y, k = 1

I q _Y k в противном случае,

где q ϕ,k и q_Y,k определяются выражениями (8) и (10), соответственно.

Оценка вероятности P _k

К одному из основных условий маскировки C_k со стороны C_i или отсутствия таковой относится непрерывность КМ _i вплоть до C_k . Учет этого требования существенно усложняет вычисление вероятности G_k,i . Однако оно не является необходимым.

Действительно, в интервале [ n 1; n 2] КМ i либо существует (событие Z ) и прерывается толь к о C_k (событие W ), либо не существует (событие Z ). В совокупности эти события определяют в известном смысле безусловную вероятность P_k,i отсутствия маскировки C_k со стороны C_i :

P ki = P ( Z ) • P ( W ) + P ( Z ) ■

Поскольку события Z и Z несовместны и образуют полную группу событий, последнее выражение можно переписать в следующем виде:

p _k , i = [i - p ( Z )] . p ( w ) + p ( Z ) = p ( w ) + p ( Z ) . p ( W ) .

По определению события Z и W также несовместны. Следовательно, произведение соответствующих вероятностей равно нулю и P_k,i = P ( W ).

Таким образом, C_k не маскируется C_i , если прерывает КМ _i , причем независимо от того, прерывается ли КМ i некоторым C j ( j e [n1; n2] j ≠ i ≠ k ) или нет.

Полученное условие отсутствия маскировки, а также интерпретация коэффициентов рассматриваемых преобразований как тональных компонент ЗС, что позволяет считать их независимыми, дают возможность определить вероятность P_k произведением:

n 2

Pk = P { Y_t >  A ( f _t )} • П (1 - Gм ), i * k , (12) i = n1

где A ( f_k ) – значение абсолютного порога слышимости на частоте f_k ; n 1 и n 2 – соответственно, наименьший и наибольший номер коэффициента преобразования, уровень кривой маскировки которого (КМ _i ) еще превышает A ( f_k ); G_k,i – вероятность маскировки C_k со стороны C_i . При этом для оценки G_k,i можно воспользоваться выражением [7]:

G k 4 = g k 4 • P {Y e [Y1 , , D i ]} ^

• x P{Y_t e [ A ( f k ), E „ ( f о , D , )]} ^{( )}

где g_k,i – безусловная вероятность маскировки C_k со стороны C_i ; Y 1 _i – значение Y_i , при котором уровень КМ _i равен A ( f_k ); Е_км ( f _o, D_i ) – уровень КМ _i на относительной частоте f o = f - f. |/ AF i , a AF i -ширина частотной группы, образованной возможно маскирующим тоном C_i .

Аналитические выражения, аппроксимирующие эмпирические зависимости Af ) и A F ( f ) , приведены в работе [8]. Там же описан метод оценки G_k i , пригодный для случаев маскировки любым участком КМ _i . Однако оценка g_k,i проведена только при маскировке левой ветвью и двумя первыми участками правой ветви КМ _i . Сложность оценки g_k,i для случая маскировки третьим участком правой ветви КМ _i обусловлена зависимостью ее крутизны от Y_i .

Относительно этого участка авторы предлагают следующую аппроксимирующую функцию:

Значение g 2 _k,i известно [7-8] и составляет 1/2. С целью оценки g 1 _k,i отобразим поведение Е_км ( f _o, Y_i ) на частоте f _o в плоскости координат Е _км, Y_{i i} на частоте f o существует лишь при определенных значениях YY e [ Y 1 i , Y 2 i ]. Тогда искомую вероятность можно определить отношением площадей S ₁/ S , где S = ( E 2 км - E 1 км ) • ( Y 2 i - Y 1 , ).

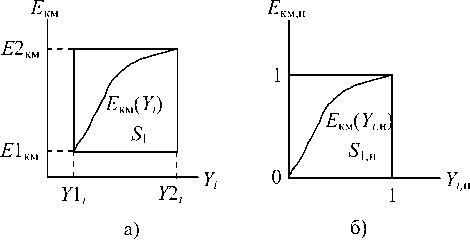
Рис. 2. Геометрическая интерпретация поведения КМ _i на частоте f _o

Для упрощения расчетов приведем область изменения КМ _i к квадрату единичной площади Y_i заменится переменной Y_i,н = ( Y_i–Y 1_i)/( Y 2 _i – Y 1 _i ), а функция примет вид:

E (Y ) = км i ,н

Е км [ Y ,h ( Y 2 i - Y1 i ) + Y1 i ] - Е км (Y1 i ) Е км ( Y 2_t ) - Е км (Y1 i )

. (16)

В результате, как следует из рис. 2б,

• g 1 k i = J E км ( Y i ,н ) dY. H ,             ⁽¹⁷⁾

где опущен коэффициент пропорциональности, обусловленный заменой переменной Y_i .

После подстановки (14) выражение (17) приводится к виду:

E км ( fo , Y )

-z , ■ lg[1 + z 2 ■ fo ■ exp(-

⁺ Y + a m ( f i ),

z 3 Y i )] +

g 1 k

где коэффициенты z₁, z₂ и z₃ определяются эмпирически, а a_m ( f_i ) – коэффициент маскировки [3]. Отсюда видно, что при фиксированной f _o вероятность g_k,i зависит только от Y_i . Следовательно, при оценке этой вероятности достаточно ограничиться частью (14), содержащей Y_i . В соответствии с этим g_k,i удобно представить суммой:

где

g k,i = g l ki + g 2 k,i ,                ⁽¹⁵⁾

где g 1 _k,i и g 2 _k,i – вероятность маскировки, обусловленная первым и вторым слагаемым (14), соответственно.

- J

lg( b + u i ,н ), ----------------du. , i, н u i,н

b = 1 z²^^^----------.     (19)

^z 2 • / о ⁺ exp( -z з • Y 1 i )

Решение (18) с учетом (15) приводит к окончательному результату:

g k , i = ^0,5

1 у (- b ) j ln(10) ^"^ j ²

Как показывают расчеты, ряд в (20) практически сходится при двадцати первых слагаемых.

Численные характеристики энергетического параметра эффективности сжатия

Для получения расчетных данных остается определить АЧХ каждого из рассматриваемых преобразований. АЧХ коэффициентов ортогональных преобразований обычно получают как преобразование Фурье над ядром h ( k,n ) данного преобразования:

N -1

H k ( j to ) = £ h ( k , n ) • e j “ n , n = 0

где N – число точек преобразования. На этом основании нормированная АЧХ имеет вид:

• - для ДПФ

  H k ( ® ) =

  
  

sin( го n 1 2)

N • sin(2 n k IN -го )

- для ДКП

H k ( ® ) =

4 • sin( ro / 2) • cos( n k / 2 N ) N • [cos( ro ) - cos( n k / N )]

x д/1 - (-1) k • cos( ro N ).

q, бит

qY,k qϕ,k

0,1           1             10   f k , кГц

Рис. 3. Энергетический параметр сжатия для ДПФ qY, бит

1 ^-------------------------------------------------------------11-----------------------------------------------

0,1            1              10   f k , кГц

Рис. 4. Энергетический параметр сжатия для ДКП

На рис. 3 и рис. 4 приведены закономерности распределения бит при кодировании модулей параметров коэффициентов ДПФ и ДКП для ЗС с рабочим диапазоном частот 20 … 20000 Гц, динамическим диапазоном 96 дБ, частотой дискретизации Fд = 44,1 кГц и N = 332. Видно, что искажения, вызванные округлением фазы, имеют приоритет только в низкочастотной области (до 1,7 кГц). В остальном диапазоне слышимых частот более точного кодирования требует модуль коэффициентов преобразований.

q

6                             ДПФ

ДКП

1         2         3         4         5

Рис. 5. Усредненный энергетический параметр сжатия: 1 – CD-качество ( F _р = 0,02…20 кГц, F _д = 44,1 кГц); 2 – цифровые системы формирования программ звукового вещания ( F _р = 0,02…20 кГц, F д = 48 кГц); 3 – высококачественное цифровое радиовещание ( F _р = 0,03…15 кГц, F _д = 32 кГц); 4 – мультимедиа ( F _р = 0,05…10 кГц, F _д = 22,05 кГц); 5 – телефония ( F _р = 0,3…3,4 кГц, F _д = 8 кГц)

Заметим, что с увеличением динамического диапазона и/или F _д обе зависимости практически не изменяются ни по характеру, ни количественно.

На рис. 5 приведена зависимость среднего числа бит q с учетом знака, необходимого и достаточного для кодирования коэффициентов ДПФ и ДКП при условии высокого качества субъективного восприятия восстановленного звука и различной ширине F _р рабочей полосы частот ЗС. Видно, что, во-первых, допустимая степень округления коэффициентов обоих преобразований практически не зависит и от этого параметра ЗС. Во-вторых, по этому показателю перспективным для целей сжатия цифровых аудиоданных следует признать ДКП. Однако окончательный вывод по этому вопросу возможен только при наличии данных относительно эффективности прореживания спектра ЗС.

Выводы

• 1.    С точки зрения округления коэффициентов гармонических дискретных ортогональных преобразований перспективным для целей сжатия ЗС является ДКП.

• 2.    При условии высокого качества субъективного восприятия восстановленного звука для кодирования каждого немаскируемого коэффициента ДКП в среднем необходимо и достаточно 3,2 бит.

• 3.    В низкочастотной области (до 1,7 кГц) требуется более точное кодирование модуля коэффициентов ДКП: 3-5 бит.

• 4.    Допустимая степень округления модуля коэффициентов ДКП практически не зависит от динамического диапазона, частоты дискретизации и ширины рабочей полосы частот ЗС.