Энергетическое соотношение для усиления спинового эффекта Холла в суперпозиции осесимметричных пучков с цилиндрической и линейной поляризацией

Элементы микроустройств могут управляться светом, в том числе структурированным светом с фазовыми и /или поляризационными сингулярностями. Поэтому большой интерес представляют световые поля с орбитальным и спиновым угловым моментом (ОУМ и СУМ). Так как СУМ заставляет частицы вращаться вокруг своих центров масс [1], формирование нужного распределения плотности СУМ может позволить одновременно манипулировать ансамблем частиц. Для формирования светового поля с определённым распределением плотности СУМ начальное поле не обязательно должно иметь ненулевой СУМ. Если начальное световое поле имеет нулевую плотность СУМ, то есть если оно линейно поляризовано в каждой точке, но затем при распространении в пространстве формируются чередующиеся области с ненулевой плотностью СУМ, то это проявление оптического спинового эффекта Холла [2, 3]. Помимо спинового эффекта Холла, оптический эффект Холла может быть также орбитальным [4, 5] или спин-орбитальным [6].

Спиновый эффект Холла может быть радиальным и угловым. Радиальный спиновый эффект Холла описан в работе [7], в которой показано, что при фокусировке радиально поляризованного оптического вихря продольная компонента вектора плотности СУМ в фокальной плоскости имеет разные знаки на разных расстояниях от оптической оси. Угловой спиновый эффект Холла продемонстрирован в ряде наших недавних работ, например в [8], где исследовался цилиндрический векторный пучок высокого порядка в остром фокусе и показано, что вблизи фокальной плоскости формируются области с разным знаком плотности СУМ на разных полярных углах.

В нашей работе [9] мы обнаружили, что спиновый эффект Холла может возникать и в параксиальных векторных пучках, то есть даже без острой фокусировки. В [9] исследован гауссов пучок с несколькими поляризационными сингулярностями, расположенными на окружности с центром на оптической оси. Такой пучок можно рассматривать как суперпозицию радиально поляризованного однокольцевого пучка Лагерра–Гаусса и линейно поляризованного гауссова пучка.

В данной работе исследуется спиновый эффект Холла в суперпозиции двух пучков произвольной радиальной формы, один из которых имеет цилиндрическую поляризацию, а другой – линейную. Таким образом, первый составляющий пучок может иметь радиальную, азимутальную, седловую [10] или другую цилиндрическую поляризацию [11]. Второй пучок может иметь линейную поляризацию с произвольным направлением, и оба пучка могут иметь произвольную осесимметричную форму, то есть они могут быть пучками Лагерра–Гаусса [12], Бесселя–

Гаусса [13], гипергеометрическими гауссовыми пучками [14] или какими-то другими более редкими пучками [15] с вращательной симметрией. В работе получено и доказано энергетическое правило, согласно которому спиновый эффект Холла является наиболее сильным, то есть плотность спинового углового момента максимальна, когда оба составляющих пучка в суперпозиции имеют одинаковую энергию.

1. Спиновый угловой момент суперпозиции осесимметричных пучков с цилиндрической и линейной поляризацией

Рассмотрим суперпозицию двух параксиальных векторных осесимметричных световых полей, одно из которых с цилиндрической поляризацией, а другое – с линейной:

E ( r , ф , z ) = C c E c ( r , ф , z ) + C l E l ( r , ф , z ) ,          (1)

где ( r , φ, z ) – цилиндрические координаты, C C и C L – коэффициенты суперпозиции, определяющие вклад пучков с цилиндрической и с линейной поляризацией.

В начальной плоскости z =0 комплексные амплитуды обоих полей имеют вид:

следующую комплексную амплитуду полей (2) и (3)

на расстоянии z :

„ /       \ / A m +1 k     ( ikr ²

Ec (r,ф,z) = (-1)   -expI — z I 2 z

X A ( p ) exp I —— l J m I---

J,           I 2 z JI z v \     ■k (ikr2

E_l ^ r , ф , z) = - 1 — exp ----

' '    z 4 2 z

^X J

E c ( r , Ф ,0 ) = A ( r )

E l ( r , Ф ,0 ) = B ( r )

cos ( m ф + а ) cos ( m ф + в )

cos y sin y

X

X

У параксиальных световых полей существенна только продольная составляющая вектора спинового углового момента. В общем виде она равна

S z = 2Im { E * E y } .

Тогда для суммы двух полей (1) плотность СУМ равна:

cos ( m ф + а ) cos ( m Ф + Р )

S z = 2Im { ( C c E c, * + C l E l, * ) * ( C c E c _y + C l E l _y ) } = (9) = C c S C, z + C L S L, z + 2 C C C L Im { E C, * E l, y + E L, * E c, y } ,

cos y sin y

В выражениях (2) и (3) A ( r ) и B ( r ) – вещественные функции, m – порядок цилиндрической поляризации, а α и β задают ее азимутальный угол [11], γ определяет направление линейной поляризации.

Параксиальное распространение света в свободном пространстве описывается преобразованием Френеля, которое в полярных координатах определя-

где S C, z и S L, z – плотности СУМ цилиндрически и эллиптически поляризованных составляющих пучков по отдельности. Очевидно, они равны нулю, и потому в формуле (9) остаётся только третье слагаемое. Подставляя в него компоненты полей (6) и (7), получим:

S z

= 2 C c C l

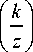
x L sin y cos ( m ф + а ) - cos y cos ( m ф + ₽ ) ] x

ется выражением

• i да 2n

E ( r , Ф , z ) =      J J E ( P , ⁰ ,O )^X

^{2 n} z 0 0

[ ^ik Г 2

x exp j— L r ² +p ²

- 2 r p cos ( 0-ф ) ^ ^p d p d 0 .

X

Для скалярного вихревого поля вида E V (ρ, θ,0)= G (ρ) exp ( im θ) интеграл по углу θ выражается через функцию Бесселя, и преобразование Френеля имеет вид:

E v ( r , ф , z ) = ( - i )

_m +i k      ( ikr ²   . J

— exp I--+ im ф lx z | 2 z       J

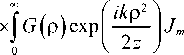
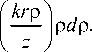
Разложив цилиндрически поляризованное поле (2) на два оптических вихря порядков ± m и воспользовавшись вспомогательным интегралом (5), получим

x Im

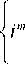
(- ik P 2 J A ( p ) exp I —2—

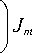
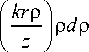
kr a i , ---lada z J

Отсюда видно, что плотность СУМ в общем случае отлична от нуля, хотя она и была нулевая в начальной плоскости. Зависимость от расстояния распространения z определяется формой конкретных пучков и предсказать её в общем виде нельзя. Так, для суперпозиции линейно поляризованного гауссова пучка с цилиндрически поляризованным пучком Лагерра–Гаусса, рассмотренной в [9], имеется дискретный набор поперечных плоскостей с нулевой плотностью СУМ, который между этими плоскостями сначала возрастает и затем уменьшается (по модулю).

Из (10) также видно, что поперечная форма распределения плотности СУМ зависит от формы обоих составляющих пучков, но не зависит от их весов в

суперпозиции, то есть изменение весов меняет распределение плотности СУМ только по величине, но не по форме. Уравнение (10) также показывает, что плотность СУМ становится равной нулю на кольцах, где компонента поля E x или E y обращается в нуль, а также когда выражение во второй строке становится действительным.

• 2.    Соотношение энергий составляющих пучков с цилиндрической и линейной поляризацией для максимизации плотности спинового момента

Таким образом, видно, что, хотя по отдельности поля с цилиндрической и линейной поляризацией не обретают спиновый угловой момент при распространении в свободном пространстве, их суперпозиция может приобретать. Поэтому возникает вопрос, при каких весах составляющих пучков в суперпозиции формируется максимальная плотность СУМ. Очевидно, плотность СУМ (10) возрастает при увеличении коэффициентов C C и C L . Но в этом случае и энергия пучка (1) также возрастает. Таким образом, чтобы сравнивать разные пучки, надо зафиксировать их энергию и положить её равной некоторому значению, например W 0 . Энергию произвольного параксиального векторного поля можно найти следующим образом:

^ 2п                   2                     2

W = J J I Ex ( r , ^ф , z )l ⁺ \^{E y} ( r , ^ф , z )l | rdrd ^ф .     (11)

Энергия цилиндрически поляризованного пучка (2) равна

WC =J A2(r)rdr x 0 2n x J ^cos2 (m ф + a) + cos2 (m Ф + ₽)| d ф =         (12)

= 2 n J A ² ( r ) rdr , 0

тогда как энергия линейно поляризованного пучка (3) равна

W l = 2 n J B ² ( r ) rdr .                             (13)

Поля (2) и (3) состоят из независимых угловых гармоник порядков ± m и 0. Тогда полная энергия пучка (1) находится как сумма

W = C C W c + C l² W l .                           (14)

Поскольку плотность СУМ пропорциональна произведению C C C L , то, чтобы максимизировать её в произвольной точке с цилиндрическими координатами ( r , φ, z ) среди всех суперпозиций (1) с заданной энергией W 0 , следует решить следующую оптимизационную задачу:

C _C C _L ^ max, c C W c + c L W l = W o .

Функция Лагранжа для этой задачи имеет вид

L ( C C , C L ) = C C C L +X o ( c C W C + C L W l - W o ) ,    (16)

где λ 0 – множитель Лагранжа.

Дифференцирование её по C C и C L приводит к двум уравнениям:

Г C L + 2 X o C C W c = 0, [ C C + 2 X o C L W l = o.

Умножая первое и второе уравнение соответственно на C C и C L , получим:

C C W c = C L W l =- C ?.                    (18)

² ^ o

Это означает, что энергии обоих пучков в суперпозиции должны быть равны друг другу и равны W 0 /2 каждая.

3.    Численное моделирование

В работе [9] исследовался случай, когда в качестве пучков с цилиндрической и линейной поляризацией были выбраны соответственно однокольцевой пучок Лагерра–Гаусса и гауссов пучок. Поэтому здесь мы можем рассмотреть некоторые другие параксиальные пучки. Например, можно сконструировать цилиндрически поляризованный пучок с несколькими световыми кольцами как суперпозицию двух пучков Лагерра–Гаусса с противоположными топологическими зарядами, с ненулевым радиальным индексом и с противоположными круговыми поляризациями и затем добавить к ним линейно поляризованный гауссов пучок с другим радиусом перетяжки. Комплексная амплитуда цилиндрически поляризованного пучка Лагерра–Гаусса в начальной плоскости определяется выражением

E c ( r , Ф , z = 0 ) = W lg^V2I — к W o.

x exp

_r ² Л cos ( m ф ) W 2 J sin ( m ф )

I ^m т f 2 r ² ^

I L m | —|x к W o ² J

где w 0 – радиус перетяжки, m и p – соответственно азимутальный и радиальный индексы, определяющие топологический заряд и число колец, W LG – нормирующий коэффициент, равный энергии пучка Лагер-ра–Гаусса и введённый, чтобы энергия пучка (19) была равна единице:

W G ₌k w[ ⁽ m + p ^{) !} 2 ^{m + 1} p !

.

Будем предполагать, что линейно поляризованный гауссов пучок горизонтально поляризован и, следовательно, имеет следующую комплексную амплитуду:

E l ( r , ф , z

= 0 ) = W G12

exp

^^^^^^ш

r ²

w 1 ²

0 ’

где w 1 – радиус перетяжки, который должен быть больше w 0 , чтобы гауссов пучок перекрывал пучок Лагерра– Гаусса, W G – нормирующий коэффициент для придания энергии пучка (21) единичного значения:

W LG

П W i ²

На рис. 1 показаны распределения интенсивности и плотности СУМ нескольких суперпозиций световых пучков (19) и (21) с разными весовыми коэффициентами.

Рис. 1. Распределения интенсивности (а – д) и плотности СУМ (е – к) нескольких суперпозиций цилиндрически поляризованных пучков Лагерра–Гаусса (19) и линейно поляризованных гауссовых пучков (21) с разными весовыми коэффициентами для следующих параметров: длина волны λ = 532 нм, радиусы перетяжки гауссовых пучков w 0 = 1 мм и w 1 = 5 мм, радиальный и азимутальный индексы цилиндрически поляризованного пучка Лагерра–Гаусса p = 2 и m = 3, расстояние распространения от начальной плоскости z = z 0 = πw 0² /λ ≈5,9 м, коэффициенты суперпозиции C C² = 0,95, Cl² = 0,05 (а, е), Cc² = 0,70, Cl² = 0,30 (б, ж), Cc² = Cl² = 0,50 (в, з), Cc² = 0,30, Cl² = 0,70 (г, и) и Cc² = 0,01, Cl² = 0,99 (д, к). Числа возле цветовых шкал обозначают минимальное и максимальное значения. Знаками «+» и «–» показаны области

соответственно с положительным и отрицательным значением плотности спинового углового момента

Рис. 1 подтверждает, что максимальная плотность СУМ достигается, когда энергии обоих составляющих пучков одинаковы, то есть C C = C L . Также видно, что плотность СУМ действительно меняется с весовыми коэффициентами только по величине, но не по форме.

Другой пример составного светового поля (1) – когда цилиндрически поляризованный пучок строится как суперпозиция двух пучков Бесселя–Гаусса [13] порядков ± m и складывается с некоторым безвихревым пучком кольцевой формы. Комплексная амплитуда цилиндрически поляризованного пучка Бесселя– Гаусса в начальной плоскости имеет вид:

E c ( r , ф , z = 0 ) = W bG² J m ( a o r ) x

П W o ²

W bg = “2“ exp

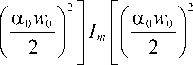
где I m (ξ) – модифицированная функция Бесселя m -го порядка.

Чтобы сконструировать безвихревой однокольцевой световой пучок, можно вычесть два гауссовых пучка с разными радиусами перетяжки w 01 и w 02 :

E l ( r , ф , z = 0 ) =

= w-^

Г r ² ^         Г r¹

expl--T l-Х expl--Г k W021J         I W022

x exp

_r ² ^ cos ( m ф ) w 2 J sin ( m ф )

где w 0 – радиус перетяжки, m – порядок цилиндрической поляризации, α 0 – масштабный множитель пучка Бесселя–Гаусса, определяющий радиус светового кольца, W BG – нормировочный коэффициент, чтобы энергия пучка (23) была равна единице:

где коэффициент χ выбирается так, чтобы поле имело нулевую интенсивность на оптической оси на некотором расстоянии z : χ = q 2 / q 1 , где q i = 1 + i λ z /(π w ² 0 i ), i = 1, 2, и W BG – нормировочный коэффициент для приведения энергии пучка (25) единичного значения:

n W 2 2i n w 2 2    2      n W 2 2i w ₀2

W dg = “V + —7- Х — 2 --rReХ.       ⁽²⁶⁾

2     2          w 21 + w 0₂

На рис. 2 изображены распределения интенсивности и плотности СУМ нескольких суперпозиций све- товых пучков (23) и (25) с разными весовыми коэффициентами.

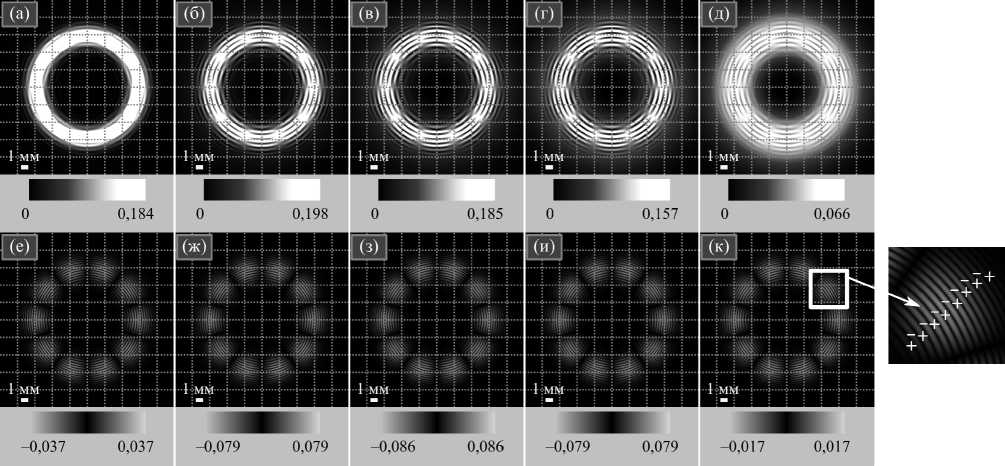
Рис. 2. Распределения интенсивности (а – д) и плотности СУМ (е – к) нескольких суперпозиций цилиндрически поляризованного пучка Бесселя–Гаусса (23) и линейно поляризованной разности двух гауссовых пучков (25) с разными весовыми коэффициентами для следующих параметров: длина волны λ = 532 нм, радиус перетяжки гауссовой составляющей пучка Бесселя–Гаусса w 0 = 1 мм, масштабный коэффициент α 0 = k /1000, порядок цилиндрической поляризации m = 5, радиусы перетяжки линейно поляризованных гауссовых пучков w 01 = 5 мм и w 02 = 7 мм (при этих радиусах световое кольцо разностного пучка имеет тот же радиус, что и у пучка Бесселя–Гаусса), расстояние распространения от начальной плоскости z = z 0 = πw 0² /λ ≈5,9 м, коэффициенты суперпозиции C C² = 0,95, C L² = 0,05 (а, е), Cc² = 0,70, Cl² = 0,30 (б, ж), Cc² = Cl² = 0,50 (в, з), Cc² = 0,30, Cl² = 0,70 (г, и) и Cc² = 0,01, Cl² = 0,99 (д, к). Числа возле цветовых шкал обозначают минимальное и максимальное значения. Знаками «+» и «–» показаны области соответственно

с положительным и отрицательным значением плотности спинового углового момента

Рис. 2 подтверждает, что и в этом случае, когда оба пучка в суперпозиции (1) отличаются от пучков с рис. 1, максимальная плотность СУМ достигается при том же условии, то есть когда энергии обоих составляющих пучков одинаковы: C C = C L . Из рис. 2 также видно, что, как и на рис. 1, плотность СУМ меняется с весовыми коэффициентами только по величине, но не по форме.

Заключение

Рассмотрена суперпозиция двух осесимметричных параксиальных векторных световых полей без спинового углового момента, одно из которых имеет цилиндрическую поляризацию, а другое – линейную. Радиальная форма интенсивности этих полей может быть произвольной. При распространении в свободном пространстве по отдельности у этих полей не возникает спиновый угловой момент и они сохраняют свою поляризацию. Суперпозиция этих полей имеет неоднородную линейную поляризацию в начальной плоскости, но при распространении в пространстве поляризация становится эллиптической и потому формируется ненулевой спиновый угловой момент. Распределение плотности спинового углового момента состоит из чередующихся областей с левой и правой эллиптической поляризацией. Такое разделение светового поля на области со спиновым угловым моментом противоположных знаков свидетельствует об оптическом спиновом эффекте Холла. В данной работе мы обнаружили и доказали два свойства этого явления.

Первое свойство состоит в том, что поперечная форма распределения плотности спинового углового момента не зависит от весовых коэффициентов суперпозиции. Веса определяют только величину спинового углового момента, но не форму его распределения.

Второе свойство (энергетическое правило) состоит в том, что если каждую такую суперпозицию нормировать на её энергию, то наибольшие значения спинового углового момента достигаются у той суперпозиции, у которой оба составляющих пучка имеют одинаковую энергию, то есть половина энергии всего пучка является энергией цилиндрически поляризованного пучка, а другая половина – это энергия линейно поляризованного пучка.

Рассмотренные суперпозиции пучков с цилиндрической и с линейной поляризацией можно формировать в интерферометре Маха–Цендера, в котором свет разделяется неполяризующим делителем пучка, затем в обоих плечах проходит через линейные поляризаторы, далее в одном из плечей свет проходит через q-пластинку, которая формирует цилиндрический век- торный пучок из линейно поляризованного, и затем с помощью второго делителя пучка свет из обоих пле-чей снова собирается в один пучок. Такая схема была реализована в нашей работе [9]. Управление энергией составляющих пучков в суперпозиции может осуществляться с помощью нейтральных фильтров.

Обнаруженные свойства можно использовать для усиления спинового эффекта Холла (увеличения спинового углового момента) световых полей. В оптическом манипулировании микрообъектами это может повысить эффективность вращения захваченных частиц вокруг их центров масс. При оптической передаче данных полученные результаты позволяют увеличить мощность сигнала, когда данные кодируются в световые пучки с помощью их поляризации, а затем входящие пучки идентифицируются поляризаторами.

Работа выполнена при поддержке Российского научного фонда (грант № 23-12-00236) в частях теории и моделирования и по государственному заданию НИЦ «Курчатовский институт» в частях «Введение» и «Заключение».