Энергетическое условие пластичности при разных по величине пределах текучести на сжатие и растяжение

• ¹    Самарский государственный аэрокосмический университет

• ²    Волжский филиал Института металлургии и материаловедения имени А.А. Байкова РАН

На основе теории пластичности анизотропных сред и использовании энергетического условия пластичности исследована возможность его представления в виде соотношения с разными пределами текучести при растяжении и сжатии. Показана невозможность существования изотропного материала с различными пределами текучести при растяжении и сжатии.

Известно, что для анизотропных сред наибольшее распространение получило энергетическое условие пластичности Мизеса. Однако оно применимо лишь для тех материалов, у которых характеристики на сжатие и растяжение одинаковы, что не всегда отвечает действительности [1], [2].

Поэтому данная статья ставит своей целью показать возможность записи энергетического условия пластичности ортотропных сред, у которых пределы текучести на сжатие и растяжение не равны между собой. Как и в условии Р.Мизеса, примем тело несжимаемым. Тогда достаточно будет рассмотреть сечение предполагаемой поверхности пластичности девиаторной плоскостью (рис. 1). Откладывая по координатным осям (оси главных напряжений) соответствующие пределы текучести на сжатие (S) и растяжение (R) и соединяя найденные точки, получим замкнутую кривую. Эта кривая будет описывать шестиугольник, предложенный Д.Д. Ивлевым [3]. Прежде чем проводить анализ поверхности пластичности в целом, необходимо рассмотреть ее

сечения координатными плоскостями. Это и позволит использовать известное свойство, что вид линии второго порядка можно определить, если даны координаты пяти точек.

В нашем случае таких точек шесть. Они позволяют общее уравнение a!!CT! + 2 a^or 2 + a 22т 2 + 2 av3P\ + 2 a 23Т 2 + a 33 = 0 при т3 = 0 записать в следующем виде:

σ 1²

R 1 S 1

+ Т

R 2 S 2

. RS .

+--

R 2 S 2

^

R з S з )

ТТ ₂ +

= 1

В процессе определения коэффициентов a_ij получена связь между пределами текучести в разных направлениях:

— + — + — = — + — + —

R ₁ R ₂ R ₃ S ₁ S ₂ S ₃

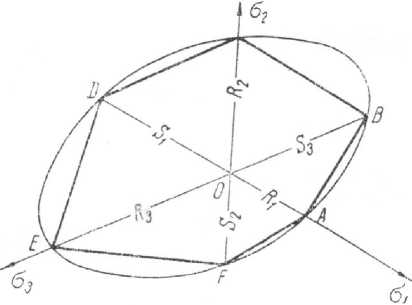
Рис. 1. Поверхность пластичности девиаторной плоскости

По аналогии запишем уравнения линий на двух других координатных плоскостях: когда т = 0

т т ( 1    1    1 )     ( 11 )

1 1 11 Тт + 1 Т +

RS 2   RS з ( R 2 S 2   R S з   R S j ²³   ( R 2   S 2 J ²

+

—

R 3

S 3

σ ₃

= 1

когда т ₂ = 0

т ₃²    Т ( 1    1    1 )      ( 11 )

1 1 1 1 тт + 11 т +

R з S з    R з S з  ( R з S з    RS 1    R 2 S 2 ) ³¹   ( R 3    S 3 ) ³

R

S 1

σ ₁

= 1

По формулам (1), (3) и (4) нетрудно оп-

Известия Самарского научного центра Российской академии наук, т. 10, №3, 2008

ределить и общее уравнение поверхности

пластичности

^Ц 31 =

σ ² σ ² σ ²

—— + —— + ——

R 1 S 1

R 2 S 2

R 3 S 3

R 1 S 1

+

----+--

R 2 S 2

R 3 S 3

I

R 1 S 1 ) ^{2 3}

R 2 S 2

I

R з s з ) ^{1 2}

---+

R 3 S 3

d ε

— dε

	Г 1    1     1 к     11 +           т + к R 1 S 1    R з S з    S 2 R 2 ) 1    S з    R з
1 =	2 σ 1     1    1 1 R 1 S 1    R 1    S 1

;

^T 1 = ^R 1

R 1 S 1

( 1

+ 1 — к R1

I т + 1

S 1 ) ¹    к R 2

I т , +1

S 2 ) ² к R з

S 3

---1 тт +

^R 2 ^S 2 ) ^{з 1}    (5)

I ^т з = ¹

С использованием выражения (2) уравнение (5) можно записать в следующем виде:

σ

σ ² σ ²

--L- +--2- +--з-

R 1 S 1

R 2 S 2

R 3 S 3

---+

R 1 S 1

+

----+

R 2 S 2

R 3 S 3

тт

RS 1 ) ^{2 3}

■ 1 ^{— т} 3 ^{) +}

R 2 S 2

В случае растяжения

довательно,

Г 1

---+--- p _к R1S1   R 2 S 2

^Ц 21

—

R з S з )

R 1 +

S 2

— + —

, сле-

—

R 2

;

тт

R з S з ) ^{1 2}

---+

R 3 S 3

R 1

S 1

(8а)

R 1 S 1

---1 тт +

^R 2 ^S 2 ) ^{3 1} (6)

Г 1

‘2 ^{— т} 3 ) = ¹

---+--- p _к R1S1   Rз S з

М з1

—

S 2 R 2 )

R 1

+

—

S 3

R 3

;

В тех случаях, когда текучесть недоста-

— + —

R 1

S 1

точно резко выражена или имеют дело с лис-

товым материалом, условие пластичности удобнее выразить через коэффициенты поперечной деформации [4]. С этой целью восполь-

При сжатии т ₁ = — S ₁ и

зуемся ассоциативным законом течения:

de = X ff (m = 1,2,3), dσ

m

c     R 2

^Ц 21

+

S 2

Г 1

---+--- к R 1 S 1    R 2 S 2

—

R з S з )

^S 1

;

— + —

R 1

S 1

где f – рассматриваемое условие пластичности.

Продифференцировав уравнение (5), найдем:

(8б)

d e _v = X I

1 R 1 S 1    R 2 S 2

R 1 S 1    R 3 S 3    S 2 f 2

I т ¹

3 _{R 1}

S 1

I ;

c

^Ц 31 =

de 2 = X

2 σ ₂

R 2 S 2

— I

1 т —

_ R1 S 1    R 2 S 2    R S з ) ¹

R 3 S 3    R 2 S 2   R 1 S 1

I т +---

³ R ₂    S ₂

;

d e з = X I

1 R 3 S 3    R 2 S 2

R 1 S 1    R 3 S 3    R 2 S 2

т + —

1    _{R 3}

S 3

.

Рассмотрим случай линейного напряженного состояния, когда т ₂ = т _з = 0 , тогда

^µ 2 ^p 1

—

d ε ₁

= X

2 σ ₁

—

S 1

;

R 3

+

S 3

Г 1

— +- к R 1 S 1    R з S з

—

S 2 R 2 )

^S 1

d ε ₂

d ε ₃

R 1 S 1

+--

R 1

= X

= X

1	1
R 2	S 2
1	1
R 3	S?

—

—

---+ к R1 s 1

+ R 1 S 1

\

—

.

--+-

R 1

S 1

Из полученных выражений следует, что

⁺ Ц

c

(

R ₂ S ₂

R 3 S 3 )

σ ₁

;

—

R 3 S 3

I т, S 2 f 2 )   ¹

.

Отсюда определим коэффициенты поперечной деформации:

^µ 3 ^p 1

+ Ц.

c

и

а

µ ₂ ^p ₁

_{µ 2} p ₁

^Ц 21

—

d e ₂ _ к

R 1 S 1 ⁺

—

d ε ₁

1 к

R ₂ S ₂

R з S з )

^т 1

+--

S 2

R 2

к R 1 S 1

+

R ₂ S ₂

—

г

к

⁺ Ц

Л

R з s з )

• R 1 s 1 ;

R 1 S 1

+

—

c

+ Ц

p

cc

^{+ Ц} 31 = ^Ц 21

R ₃ S ₃

R 2 S 2 )

• R s 1 ;

^{+ Ц} 31    ² ,

^{+ Ц}31 = ¹

Аналогично рассматривая два других

случая линейного напряженного состояния,

когда σ ₁

= т ₃ = 0 и т ₂ = т 0 , найдем:

2 σ   1

—L +

;

-

X

R 1 S 1

R 1

S 1

(8а)

^Ц 12 ^{+ Ц}

c

---+--- к R1S1   R 2 S 2

—

к

R з S з )

• R 2 s 2 ;

µ3p2 + Ц32 1R 2 S 2 + 1 R3S3 + 1 + R1S1 у • R 2 s 2; µ1p3 + Ц» — ' 1 + 1 1 ) • R 3 s 3; V R 3 S 3 R1S1 R 2 S 2 J µ2p3 + Ц23 — (1 + 1 1 Л • R 3 s 3; V R 2 S 2 R3S3 R1S1 у ppc c

^Ц 12 + ^ 32 — ^ 32 + ^ 12 — 1;

^Ц 13 + ^ 23 ^— ^ 13 +

Откуда

Ц р + ^Ц 21 _— R 1 S 1 _;

^Ц 1 Р + ^Ц 12    ^R 2 S 2

^Ц 31 + ^Ц 31 _— ^R 1 ^S 1 _;

^Ц 1 "3 + ^Ц 13    R 3 S 3

(Ц32 + Ц32 )(ц|"3 + Ц13 ) — С pc

^Ц 23 + ^Ц 23

c

^Ц 23 ^{— 1.}

^Ц 32 + ^Ц 32 _— R 2 S 2 _;

^Ц 23 + ^Ц 23    R 3 S 3

1 "1 + ^Ц 12 Х ^ Р + ^Ц 31 )

Ц ^р + 21         ^.( )

Кроме соотношений (9), (10) и (11), мож- но показать, что

^Ц 12 _ ^Ц 12 _ ¹ ^_; ^Ц 21 _ ^Ц 21 _— ^{1 1}

R2    S2    S1

ц 322 _ ц 32 _— JL

R2     S2    S3

ц ,Р _ ц ,3 — J R3       S3      S1

R 1 S 1 S 2 R 2

^Ц 23 _ ^Ц 23 _— ¹¹ .

R3

µ3p1

Т"S"

S 2 R 2

S T ^_ ^г^;(¹²)

С помощью полученных зависимостей условие пластичности преобразуется к виду:

R,S, — ¹ ( ц-p + Ц ) С ст, _ t r ₂ ) 2 + ( ц₂Р + ц " ) ^{Ц 32 + Ц 32} ( ст₂

1  1              21       21      1       2           21       21 p _c 2

² L                                        ^Ц 12 ^{+ Ц} 12

^{+ (} S 1 ^_ R 1 Х ° "1 ^{_ а} 3 ^{)+ (} ц " 1 R ^_ Ц 2 Р S 1.1 ^ 2 ^{_ а} 3 )

^_ т 3 ^{) 2 + (} Ц 3 ^{р +} Ц 3 ° 1 ) ^{( ст} 3 ^_ ^ 112 J +

Полученное условие пластичности геометрически интерпретируется эллиптическим цилиндром. Его ось равнонаклонена к координатным плоскостям и смещена относительно начала координат. Величина этого смещения зависит от показателей анизотропии и в плоскости ст3 — 0 составляет:

_с« _— ( R 1 _ S 1 fe+ Ц» ) + 2 ( R 2 _ S 2 ) .

• ²      4 _ ( ц Р 1 + Ц 2 1 )( Ц 1 Р + Ц )    ’ (14)

_т« _— ( R 2   s 2 ) С ц 2 ^р 1 + Ц 2, ) + 2 ( R 1   s 1 )

4 _ (ц2Р1 + Ц21 ХЦ12 + Ц"2 )

Выводы

• 1.    Показана возможность записи энергетического условия пластичности ортотропного тела (6) и (13) с разными пределами текучести при растяжении и сжатии.

• 2.    В полученное условие пластичности входят пять независимых показателей, отражающих анизотропию тела.

• 3.    При использовании принципа несжимаемости невозможно существование изотропного материала с разными пределами текучести на растяжение и сжатие. Это видно из выражений (2) и (12).