Энергетика тангенциального подводящего устройства микротурбины системы терморегулирования перспективного космического аппарата

Анализ информации о современных зарубежных разработках в области использования двухфазных контуров (ДФК) на космическом аппарате (КА), имеющих высокое энергопотребление, показывает техническую перспективность использования их в системах терморегулирования. В числе КА с использованием фазового перехода в системах терморегулирования упоминаются «Эврика», «Колумб» NASA, на которых были успешно проведены натурные испытания высокоэффективных двухфазных модулей. На КА COMET (NASA) обеспечение теплового режима индивидуальных теплонапряженных блоков полезной нагрузки осуществляется с помощью систем терморегулирования (СТР) на капиллярных насосах. На КА STENTOR (NASA) в СТР также используются капиллярные насосы в раскрывающейся конструкции излучательного радиатора. Проведенные натурные испытания на этих КА показали высокую эффективность СТР на базе двухфазных контуров.

Применение генерации с использованием контуров на низкокипящих рабочих телах на кораблях для дальних космических полетов для их энергообеспечения было предложено в СССР еще в 70-е гг. прошлого века. В качестве источника тепла для силового паротурбинного цикла использовались унифицированные модули радиоизотопного источника (Pu-238) [1]. Результатом исследований стала установка номинальной мощности 1,3 кВт, массы 205 кг и оснащенная холодильником-излучателем площадью 10,8 м2. На стендовых испытаниях массовый расход через контур достигал 0,0107 кг/с. Установка проработала 20 ч. За это время существенных отклонений параметров не было выявлено.

Для решения задач по терморегулированию перспективных крупногабаритных КА и станций с увеличенным энерговооружением при необходимости снижения относительных массы и размеров СТР КА наиболее перспективный путь – это создание базовых элементов интегрированных СТР КА с ДФК, как наиболее эффективной по сравнению с существующими в настоящее время в отечественной и в зарубежной практике средствами терморегулирования. При существующих системах необходимо значительно увеличивать площади наружных радиаторов-излучателей, что приводит к увеличению их массы и габаритов. Совмещение системы терморегулирования с паровой турбиной позволяет отводить часть энергии через паровую турбину в систему энергоснабжения, что уменьшает тепловую нагрузку на радиатор-излучатель. Проблема радиаторов-излучателей возникает при ограниченных возможностях размещения их под обтекателем ракеты-носителя на участке выведения КА на орбиту.

Основное техническое предложение

Содержание технического решения определяется в соответствии с источниками [2–4]:

– прямой цикл на низкокипящих телах с выработкой механической энергии. В качестве источника энергии используется внутренний источник тепла КА – тепло, выделяемое работающими приборами и установками. В традиционной схеме это тепло отводится в космос с помощью холодильников-излучателей. Предлагаемый вариант позволяет сэкономить энергоресурсы и вырабатывать механическую энергию, а также сократить площади холодильников-излучателей;

– прямой цикл на низкокипящих телах с выработкой механической энергии с использованием в качестве источника солнечного тепла, снимаемого с солнечных панелей. В связи со сравнительно низкими равновесными температурами панелей имеет низкую эффективность, однако позволяет использовать солнечное излучение в более широком инфракрасном (тепловом) диапазоне. Установки, изготовленные по этому способу, не подвержены старению и деградации характеристик (по сравнению с солнечными батареями);

– то же, что и в предыдущем пункте, с применением солнечных концентраторов параболического типа. Позволяет получить высокие температуры, а значит и высокую эффективность установки. Однако в этом случае необходимо решить проблему высоких перепадов давления рабочего тела в системе.

Конструктивная схема микротурбины

В теории турбостроения в основном используется соотношение для расчета и проектирования ступени турбин высокой быстроходности nst = 24 как осевой, так и радиальноцентростремительной схемы [2; 5–9]. Этой теме посвящены большая часть литературы, касающейся различных отраслей турбостроения: турбины большой электрогенерации (электростанции), турбины транспортных устройств (летательные аппараты, наземный, железнодорожный транспорт, различные устройства специального назначения и т. п.). Большая часть турбин проектируется как ступени активного типа большой мощности, больше 100 кВт. В области распределенной энергетики и практического использования низкопотенциального бросового тепла используются турбины радиально-центростремительного типа мощностью менее 100 кВт с коэффициентом быстроходности nst = 60 [4; 6; 10]. В основном применяется соотношение газовой динамики на сверхкритических (сверхзвуковых) перепадах давлений и температур. Тема расчетов конструкций и оптимизации параметров изложена достаточно объемно. Для диапазона низкой быстроходности nst < 60 тема недостаточна раскрыта в части инженерных расчетных приложений, что вызывает очевидные трудности при моделировании подобных объектов мощностью меньше 100 кВт. На сегодняшний момент для утилизации энергии газотранспортных систем и систем добычи углеводородов используются турбины различных специальных конструкций: в том числе вихревые, безлопаточные – центробежные и т. п. [7].

В нашем случае турбины мощностью менее 1 кВт можно идентифицировать (классифицировать) как микротурбины малой быстроходности, размерности и мощности [11]. Вопрос оптимального проектирования и выбора типа турбины остается открытым из-за низкого КПД тихоходных турбомашин, имеющего сходные значения для микротурбин лопаточно-осевого и радиального типа, лабиринтно-вихревых, дисковых турбин, турбин центробежных и центростремительного типа и т. п. Отдать предпочтение какому-то типу на данном этапе невозможно. Стоит отметить, что для турбин как активного, так и реактивного типа важнейшим элементом, формирующим окружное направление потока, обеспечивающего окружную работу рабочего колеса, является сопловой или направляющий аппарат для быстроходных турбин, выполненных в виде сопловых решеток (в лопаточном венце). Для тихоходных и малорасходных машин выполняется одно сопло (сопловой тангенциальный канал) [2]. Диапазон выходной мощности по техническому заданию заказчика составляет от 100 до 1000 Вт на дозвуковом перепаде рабочего тела (пара), при перепаде температур не более 60 ºС с ограничением оборотов до 5000 об/мин из-за требований высокого ресурса. При таких данных не стоит ожидать высоких КПД, сравнимых с КПД турбин большой энергетики. Задача оптимального проектирования с целью наивысшего достижения КПД является актуальной. Для постановки задач исследования спроектирован и изготовлен прототип микротурбины с генератором с характерными элементами конструкций на базе центростремительного рабочего колеса детандера (рис. 1).

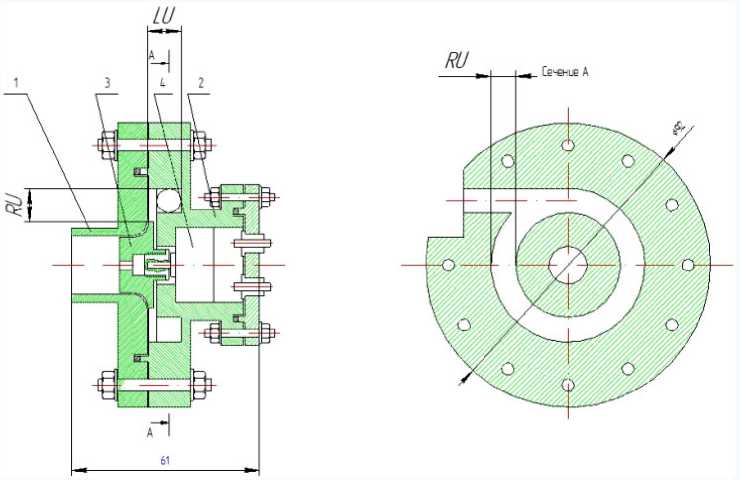
Рис. 1. Прототип микро турбогенератора:

1 – крышка; 2 – корпус микротурбины с тангенциальным подводящим устройством; 3 – рабочее колесо; 4 –генератор

Fig. 1. Prototype of a microturbo generator:

• 1 – cover; 2 – microturbine housing with tangential supply device;

3 – impeller; 4 – generator

Из конструкции видно, что тангенцильный канал является основным элементом, формирующим окружное течение потока. Конструктивно следует выделить область радиальноокружного потока RU и осе-окружного потока LU. Общий вид турбогенератора показан на рис. 2.

а

б

Рис. 2. Вид на рабочее колесо со стороны крышки ( а ); крышка и корпус генератора ( б ); вид со стороны крышки генератора ( в )

в

Fig. 2. View of the impeller from the cover side ( a ); сover and housing of the generator ( b ); view from the side of the generator cover ( c )

Цель и постановка задачи исследования

Существующие на сегодняшний день конструкции СТР автономных КА с длительным сроком активного существования (до 15 лет) используют практически весь спектр известных конструкторских решений: естественную теплопроводность от источника до радиатора-излучателя в черный космос; сложную конструкцию системы транспортных тепловых труб; жидкостноконтурную передачу тепла с южной на северную панель, ДФК с динамической (насосной) системой подачи в контуре до контурной тепловой трубы. Указанный перечень в последовательности обеспечивает рост массоэнергетической характеристики системы СТР [12]. Следует отметить, что габариты северной и южной панелей определяются площадью испарителя и конденсатора СТР, интегрированных в сотопанели, и определяют, в основном, габариты и силовую схему КА в целом. Следующий логический шаг – рекуперация электрической энергии в системе двухфазной СТР на основе органического цикла Ренкина с целью снижения тепловой нагрузки на конденсатор-излучатель. Самым важным узлом такой системы является турбопривод, состоящий из подводящего устройства, обеспечивающего поле скоростей и давлений на входе в последующее рабочее колесо турбины. Для турбин малой быстроходности с малорасходным парциальным подводом характерна значительная несимметричность полей термодинамических параметров, приводящая к значительным отклонениям в результатах расчета по методикам полноразмерных агрегатов. В соответствии с изложенным, следуя поставленной цели повышения массоэнергетических характеристик двухфазных СТР за счет применения турбогенератора в цикле Ренкина, необходимо решить следующие задачи:

– разработать и изготовить комплект типоразмеров подводящих устройств с целью получения энергетических характеристик в диапазоне изменения конструктивных и режимных параметров;

– провести экспериментальные исследования энергетических характеристик подводящих устройств с оформлением базы данных по основным конструктивным и режимным параметрам.

Методика проведения энергетических и частичных балансовых испытаний микротурбин

Энергетические испытания проводятся с элементами балансовых испытаний, возможных на материальной части физического макета с дополнительной установкой измерительных (станций) постов: p ^* – полного давления; р – статического; T изм – измеренной равновесной температуры.

Расположение постов (измерительных станций), с целью коррекции расчетного алгоритма, полностью совпадает с принятой расчетной схемой (рис. 3).

Последовательности постов измерений соответствует:

- пост измерений перед входом в канальном подводе p * , p вх , Т * _х = Т _вх;

– в канале подводящего устройства p 0 , p ₀ ^* , Т 0изм ;

– на выходе из канального подводящего устройства, на входе в рабочее колесо p 1 , p ₁ ^* _u , Т 1изм , где p ₁ ^* _u – измеряется в окружном направлении;

– на выходе из рабочего колеса на радиусе R 2 , p 2 , p ₂ ^* _u , Т 1изм .

Поскольку технически сложно разместить приемник полного давления на радиусе R 1 , продувка канальных подводящих устройств проводится в специальном приспособлении, без рабочего колеса, на радиусе входа в рабочее колесо. При необходимости эти испытания согласуются по p 1 – статическому давлению при энергетических испытаниях.

Методика обработки результатов на участке /вх – о/.

Измеряемое p _в ^* _х, Т _в ^* _х, p 0 , p ₀ ^* , Т 0изм , М 0 , Т 0 , τ f 0 , С 0 .

Дополнительно рассчитывает массовый расход двумя способами для исключения промаха.

где

□ m = Р0C0 • F0 =Ро • F0 • m• qf0,

m =

k +1

, ( 2 ) k -1 1

k                  • ,

\ ( k + 1 J R

k +1 k + 1 ) 2 ( k -1 )

M 0

k +1

. k - 1 , . ) 2 ( k -1 )

1 +Mn

2        ⁰ )

F 0 = h 0 ∙ b 0 – площадь проходного сечения канала подводящего устройств. Коэффициент потерь ζ вх рассчитывается:

*

^{2 k} P вх С о • ( k - 1 ) ^Р вх

*

p ⁰

Ро J

=^

Методика обработки результатов на участке /0 – 1/.

Измеренные: p ₁ ^* _u , p 1 , Т 1изм .

Известны: p 0 , p ₀ ^* , Т 0изм .

Рассчитываются по выражениям для окружной составляющей С 1 u :

M 1 u , T 1 u , τ f 1 , С 1 u , p u , Т 1 u .                                               (5)

Параметры рассчитаны по окружной составляющей С _{1 u} , необходима коррекция:

С 1 = V C 1 u ⁺ C 1 R •

где С _{1 R} – радиальная составляющая абсолютной скорости на входе – определяется в первом приближении p 1 = p 1 _u и

С 1 R =

th            tn

Р 1 • F 2     Р 1 • 2n R 1 • b 1 ’

где ṁ (1).

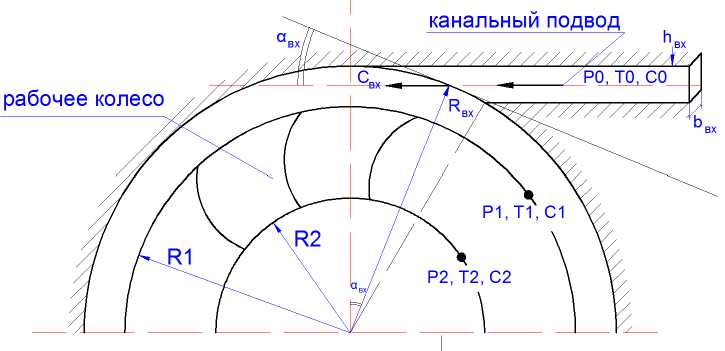
Рис. 3. Расчетная схема радиальной ступени

Fig. 3. Design scheme of the radial stage

Корректируется полное давление:

*        C 2 k - 1

^p1 = pl ⁺ T • T'

И совершается прогон пока:

С ¹ i ⁺¹ - C ¹ i <  0,01.

^C1i +1

При известных С 1 , С 1 u , С 1 R рассчитывается угол абсолютной скорости:

^C a = arctg— 1 ^й- . C 1 u

Угол относительной скорости:

CC p, = arctg---- 1 ^й— = arctg------ 1 ^й ,

¹         C 1 u - U 1         ( C 1 u -® 1 • й )

W1 =

I C 1 u - U 11

cos Р 1Л

Угол атаки:

i = 3 1 л -3 1 ,

где β 1л – конструктивный параметр.

Коэффициент потерь сопла (подводящего аппарата):

**

Pol _ pl, 3L_

Ip o P 1 J C 2 ( k - 1 ) •

Описание и конструктивные особенности исследуемых канальных подводящих устройств

Экспериментальная продувка канальных подводящих устройств производилась в специальном приспособлении, имитирующем энергетическую установку и позволяющем производить измерения по шести измерительным постам, согласно схеме (рис. 4).

Измерительный пост на входе pвх, Tвх, измерительный пост в канале подводящего устройства p0 T0 и четырех измерительных постах на радиусе рабочего колеса p1T1, p2T2, p3T3, p4T4. На посту p2T2 измерения не производились, пост резервный. На каждом посту измерялись полное давле- ние (p*) приемником полного давления и статическое давление (pст) приемником статического давления, равновесная измеренная температура (t) – термопарой.

Экспериментальная установка с размещенными приемниками полного и статического давления показана на рис. 5.

Для геометрических параметров используются следующие определения и расчетные соотношения:

– l _вх – плечо момента количества движения, где:

l = R - h / 2; вх вх

– dг экв– диаметр горла эквивалентный, где dг.экв

4 ⋅ b ⋅ h

;

π

– ε – степень парциальности, где

α             R -h

ε = ^вх , α = arccos ^вх ;

2π вх вх

Re 0 – число Рейнольдса по скорости С 0 , где

C0 ⋅ dг.экв Re0 =

v

Reω – число Рейнольдса по окружной скорости, где

C l ω⋅l 0 вх вх Reω =      =

νν

– l _вх/ R _{1 k} – относительное плечо момента количества движения, где R _{1 k} = 24 мм – радиус входа в рабочее колесо микротурбины.

Спиральное подводящее устройство формируется совмещением двух радиусов профилирования R 1 и R 2 со смещением центров профилирования на величину Δ.

Обмеряемые параметры спирального подводящего устройства микротурбин:

b = 3,5 мм – ширина канала;

D – внешний максимальный диаметр;

δ – расстояние от D до верхней (ближней от D ) поверхности канала h ;

• L 1 – максимальной расстояние по линии диаметра D ;

• h – ширина входного канала;

• R 1 – больший радиус профилирования;

• R 2 – меньший радиус профилирования;

• Δ – смещение центров профилирования;

• ε – степень парциальности;

• l вх – плечо входного канала по средней линии;

• h / R _{1 k} – относительная ширина входного канала;

• l _вх/ R _{1 k} – относительное плечо входа.

  4 ⋅ b ⋅ h

  
  

  .

  
  

  ^d г.экв

  
  

π

Выражения для обсчета спирального поводящего устройства по результатам обмера:

L ₁ = R ₁ + R ₂ + 2Δ;

Δ = 0,5 h+ δ + 0,5 L ₁ ⋅ 0,5 D ,

R ₁ = D - 2δ - 0,5 h - 0,5 L ₁,

R 2 = 0,5 (L1 - h), lRX = 0,5D - 5 - 0,5h, вх

1_Ю - 0,5 h a = arccos вх------- , ^вх           l вх + 0,5 h

^ BX ε. 2π

Выражения для обсчета кольцевого поводящего устройства:

L ₁

R1 = 2, lBX = 0,5L - 0,5h, или lBX =R1 - 2

Приняты следующие обозначения для сборников C – спиральный, первая цифра в обозначении: высота h в мм. Вторая цифра в обозначении: l вх плечо момента количества движения в мм (округлено). Например: C 6–39 – спиральный h = 6 мм, l _вх ≈ 39 мм; К 6–32 – кольцевой h = 6 мм, l вх ≈ 32 мм.

Согласно обозначениям, количественные значения параметров 19 спиральных и 13 кольцевых подводящих устройств представлены в табл. 1.

Таблица 1

Диапазон конструктивных параметров спиральных и кольцевых подводящих устройств

Обозначение	h (мм)	l вх (мм)	d rэкв (мм)	l вх / R 1 k	h / R 1 k
С2…6–28…39	2–6	28–38,9	3–5,2	1,16–1,62	0,083–0,25
К2...6–25...32	2–6	25–32	3–5,2	1,04–1,33	0,083–0,25

Диапазон изменения геометрических параметров в безразмерном (относительном) виде (22 конструктивные сборки):

Re 0 = 10000–60000 = 1 – 6∙10⁴ – число Рейнольдса по скорости С 0 ;

• l вх / R 1 k = 0,97–1,62 – относительное плечо входа;

• h / R _{1 k} = 0,083–0,25 – относительная ширина входного канала;

• b = 3,5 мм – ширина канала;

R 1 k = 24 мм – радиус входа в рабочее колесо микротурбины.

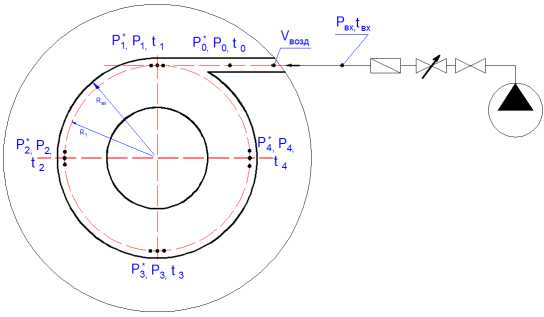
Рис. 4. Схема расположения датчиков в испытательной системе

Fig. 4. The layout of the sensors in the test system

Рис. 5. Экспериментальная установка с приемниками полного и статического давления

Fig. 5. Experimental installation with full and static pressure receivers

Методика обработки экспериментальных испытаний тангенциального подвода дозвуковой центростремительной турбины

Для разработки математической модели и алгоритма расчета центростремительной микротурбины, применяющейся для утилизации тепловой мощности КА, необходимо оценивать окружную составляющую абсолютной скорости на радиусе входа в рабочее колесо (РК) турбины. Теоретический анализ суммарных потерь потока как суперпозиция внезапного расширения с последующим вихревым течением до рабочего колеса представляет теоретически неопределенную задачу. Для предварительной оценки и формирования базы данных потерь на этом участке необходимо использовать данные экспериментальных продувок с регистрацией энергетических и скоростных параметров потока на участке: 0 – параметры во входном канале устройства; 1 – параметры на входном диаметре во входном канале устройства. Для обработки экспериментальных данных помимо коэффициента потерь энергии ζ₀₁ удобно воспользоваться коэффициентом окружной составляющей скорости φ _u [13–15].

Обоснуем некоторые соображения, определяющие содержание коэффициента окружной составляющей скорости.

Определим массовый расход в подводящем канале:

• •             m 7    7

  
  

m = p V = С0 • h0 • b0

где ρ – плотность; C ₀ – расходная скорость в канале; h ₀ – высота канала; b ₀ – ширина.

Допустим, что C ₀ – const по высоте h ₀, плечо момента количества движения по h ₀ изменяется от l ₁ до l ₂, тогда момент количества движения во входном сечением запишется как интеграл:

l 2                                                           2 _l

M 0 = J p. C 02 • l • b 0 • dl = p. C 0 • h 0 • b 0 • C 0,2 ₄ .

Подставим пределы интегрирования l 2 R 0 ; l 1 = R 0 – h 0 и учтем (13):

M 0 = mi • C 0 • 2 ( 1 2 - 1 1² ) ,

M 0 = 1 m • C 0 ( 2 R 0 h 0 - h 0² ) = m • C 0 h 0 ^ R 0 - h ⁰

.

Теоретический момент количества движения на текущем радиусе R :

М Т = m • U_T • R ,

где ṁ – массовый расход определяется выражением:

m = 2nR ■ b ■ CR ■ p.

Для идеального случая, когда нет момента сил трения, моменты M 0 и М равны:

M 0 = М Т ,

Подставив выражения для моментов (16), получаем:

hi ■ C 0 ■ h ₀ I R - -2- 1 = hi ■ U_T • R ,                                   (18)

Продолжим преобразование, выразим значения окружной составляющей на текущем радиусе

через параметры во входном канале:

и = СА Гr—1h

^T     R i        2

или с учетом

R O = ¹ вх + "2"»

С ₀ h ₀

^UT = _D ■ ¹ вх , R

Для радиуса входа в рабочее колесо R ₁ при отсутствии потерь

Uir = С      ■ 1bx,

1 T              вх

R ₁

Коэффициент окружной составляющей скорости определяется

Ф

u

= U 18_

^U 1 T ^,

где U _{1 d} - действительное (измеренное) значение; U _1т - максимально теоретически возможное.

Действительное значение окружной скорости рассчитывается как среднее по результатам измерений полного и статического давлений и температуры по периферии рабочего колеса микротурбины в 4 точках окружности R 1 (рис. 4).

Общий вид сборки представлен на рис. 6, где показана подводка к термисторам, приемники давления не подключены к измерительным трубкам датчиков давлений.

Для предварительной оценки окружной скорости на входе в РК микротурбины необходимо использовать уравнения энергии по периферии РК:

k   p0   C02    k p1   C12

1=1+ Z , к -1 р0    2 к -1   р12 где Zc — коэффициент потерь полного напора в сопле; абсолютная скорость на входе в РК:

С12 = U12 + CR1,(24)

расходная составляющая определяется только расчетно:

m &

CR1 =

Р 1 F 1

где ṁ – массовый расход рабочего тела; ρ 1 – плотность на входе в РК; F 1 – площадь проходного сечения в РК.

Коэффициент скорости представляет собой параметр, рассчитанный непосредственно по результатам измерений без дополнительных допущений. По результатам эксперимента в диапазоне изменений геометрических и режимных параметров подводящего устройства микротурбины (h0 – высота канала; lвх – среднее плечо момента количества движения; R1 – радиус входа в рабо- чее колесо; Re – число Рейнольдса на входе) реализуется возможность формирования базы данных для φu с целью использования при математическом моделировании и проектировании микротурбины.

Рис. 6. Общий вид сборки

Использование баз данных по коэффициенту окружной составляющей скорости φ u (22) и коэффициенту потерь полного давления ζ с (23) позволяет однозначно определить полное давление на входе в РК микротурбины при математическом моделировании и проектировании, а также проводить оптимизацию в диапазоне изменений режимных и геометрических параметров микротурбины.

Алгоритм обработки экспериментальных данных испытаний тангенциальных, спиральных и кольцевых подводов реализован в виде программного алгоритма, позволяющего по замерам в 0 (канальном подводе) и 1 сечении (по периферии рабочего колеса), значений давлений, температур и расчетных скоростей определять энергетические параметры подводящего устройства: ζ _с – коэффициент потерь (12) и φ _u – коэффициент скорости (21).

Fig. 6. General view of the assembly

Согласно конструктивным схемам материальной части по спиральным и кольцевым подводящим устройствам, проведены экспериментальные замеры коэффициента потерь ζ с0 и φ u в диапазоне изменения геометрии подводящих устройств (табл. 1, 2) и режимного параметра Re 0 , рассчитанного по значению скорости C 0 ( U 0 ) в тангенциальном подводе. Данные представлены в виде базы данных в табл. 2, 3. В общем случае база данных представляет собой табличную функцию коэффициента потерь Z с о = ( L_вх/ R 1 к , h / R₁ к ,Re o ) ; коэффициента скорости

Ф u = ( L _вх / R₁ k , h / R₁ k , Re₀ ) ; от трех переменных:

L _вх/ R _{1 k} – относительное плечо входа;

h / R 1 k – относительная ширина входного канала;

Re 0 – число Рейнольдса по скорости С 0 ( U 0 ) в тангенциальном канале.

По табличным данным визуализация поверхности уровня функция достаточно монотонна, не имеет резких экстремумов и достаточно легко апроксимируется даже линейными сплайнами (рис. 7). Значение функции в 2–3 раза превышает коэффициент потерь на внезапное расширение. Очевидно, в структуре энергетических потерь должен присутствовать дополнительный элемент. В качестве такого элемента следует рассмотреть потери энергии потока при течении потока от радиуса R0 до радиуса R1k, что следует из конструктивной геометрии подводящего устройства. Для оценки коэффициента потерь на радиально окружном участке течения воспользуемся численной оценкой по данным испытания кольцевого подводящего устройства К2-25. В качестве исходных данных для расчета используем значения R = lвх + h /2 = 0,026 м; AR = Ro -Rk = 0,002 м; 5” = 0,00017 м; Cu0 = U0 ■ R0 = 2,314[м2/с]. Коэффициенты потерь рас- считываются по выражению, полученному из уравнения энергии:

k   p0  U0 k    p1  U1

к -1  р0    2    к -1   р1    2    Z рад'уч' 2 , откуда ζрад.уч:

^                        2Т^г-2Т^г ^

Ср.,, = 772 ГГо(Р0-Рк) + "^ '(26)

и 0 ^ k 1 р               2

Следует отметить, что коэффициент потерь на участке радиального течения формируется за счет падения статического давления и окружной составляющей скорости. В одномерном потенциальном течении изменение полного и статического давлений совпадает, скорость не изменяется. Результаты расчетов представлены в табл. 4 [16–17]. Из результатов видно, что коэффициент потерь при изменении Рейнольдса изменяется практически в два раза и близок к единице. Коэффициент потерь формируется из двух приблизительно одинаковых членов: потерь статического давления, потерь окружной скорости.

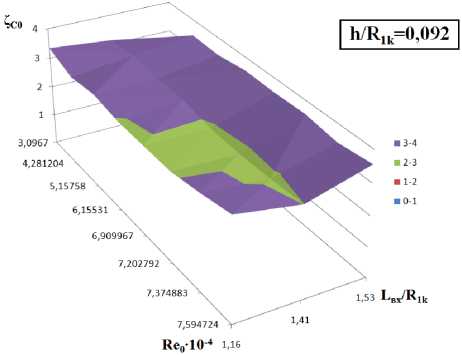
а

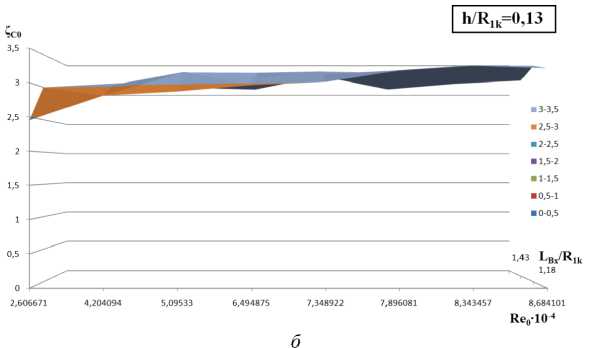
Рис. 7. Поверхности уровней функции (базы данных) Z с 0 = ( L вх / R 1 k , h / R 1 k , Re 0 ) : а - относительная ширина входного канала h / Л 1 k = 0,092 ; б - h / Л 1 k = 0,013

Fig. 7. Surfaces of function levels (databases) Z _{с 0} = ( L вх / R 1 k , h / R 1 k , Re 0 ) : a - relative width of the input channel h / A 1 _k = 0,092 ; b - h / A 1 _k = 0,013

С учетом данных коэффициента на внезапное расширение и коэффициента потерь, на радиальном участке остается приблизительно 1/3 от общего коэффициента потерь, т. е. величина приблизительно равная единице. В качестве гипотезы предлагается эту величину оценить коэффициентом потерь на разворот потока на 90º по формуле Вейсбаха [14]:

Z_M = 0,95sin ² 1 — I + 2,05sin 4 | ^— | = 0,986, м_{2 2}

где 8 = 90° - угол разворота, с учетом поправки коэффициент потерь на разворот Z _пов = С 1 • A "Z _M; С 1 = 1 для симметричного течения; А = 0,95 + 33,5/ 8 = 1,32; тогда коэффициент разворота на Z 90 _o = 1,3. Следует обратить внимание, что предложенная энергетическая балансировка потерь на внезапное расширение, радиальный участок и разворот потока на 90º дает величину, размещенную в базе данных по коэффициенту потерь ζ С 0 в подводящем устройстве (табл. 2, 3).

Коэффициенты потерь ζ_С0 и скорости φ _u для кольцевого подводящего устройства

Таблица 2

К 2-25					К 6-32
ζ С 0	L вх/ R 1 k	h / R 1 k	Re 0	φ u	ζ С 0	L вх/ R 1 k	h / R 1 k	Re 0	φ u
3,0209067	1,04	0,083	17520,65	0,2889737	2,6914906	1,33	0,25	28199,46	0,350395
2,81332385	1,04	0,083	21327,45	0,4220766	1,3009716	1,33	0,25	24833,99	0,5772179
2,7729739	1,04	0,083	26275,56	0,4445341	1,2320646	1,33	0,25	31322,3	0,5997001
3,1156121	1,04	0,083	29045,19	0,3552896	1,732688	1,33	0,25	39639,36	0,5403541
2,8642894	1,04	0,083	30264,05	0,4435942	2,0409651	1,33	0,25	44025,96	0,5012578
2,880883	1,04	0,083	32048,86	0,4319966	1,7411898	1,33	0,25	47618,09	0,5481886
2,7712986	1,04	0,083	32068,46	0,4661496	1,8086491	1,33	0,25	50644,91	0,541099
2,8155358	1,04	0,083	30754,69	0,4596947	1,7884947	1,33	0,25	50892,56	0,5436699

Коэффициенты потерь ζ _{С 0} и скорости φ _u для спирального подводящего устройства

Таблица 3

С 2-28					С 6-39
ζ С 0	L вх / R 1 k	h / R 1 k	Re 0	φ u	ζ С 0	L вх / R 1 k	h / R 1 k	Re 0	φ u
3,3439123	1,16	0,083	30933,17	0,2453211	1,7325754	1,62	0,25	19870,44	0,4304552
3,01471724	1,16	0,083	38247,2	0,3147172	2,6571707	1,62	0,25	30967,94	0,3141631
3,1387546	1,16	0,083	45548,23	0,3981814	1,9631256	1,62	0,25	32378,77	0,4201886
2,98048791	1,16	0,083	55432,55	0,3672183	2,1385318	1,62	0,25	40561,44	0,4038012
2,9605327	1,16	0,083	60051,83	0,3609476	2,0742571	1,62	0,25	44835,47	0,4082927
2,9455596	1,16	0,083	64664,08	0,3731699	1,8497709	1,62	0,25	52284,86	0,4391877
3,12578929	1,16	0,083	67022,12	0,3387341	1,801266	1,62	0,25	54236,36	0,445411
3,3556589	1,16	0,083	69246,83	0,2580974	1,6874583	1,62	0,25	58712,84	0,4565281

Таблица 4

Результаты расчетов коэффициентов потерь на радиальном участке течения

№	С 0 i ( U 0) [м/с]	* p 0 [Па]	p 0 [Па ]	τ 0α [Н/м2]	dC u / dR [м/с]	C u 0 [м2/с]	Δ Cu 0 [м2/с]	C uk [м2/с]	U k [м/с]	Δ p [Па]	pk [Па]	2 k   p 0 - P k ( k -1 ) p    U 02	2 L U 1 1 " I U о J	ζ рад.уч.	Re 0
1	89	103750	98955	31,4	408,2	2,314	0,816	1,5	62,4	662	98923	0,487	0,508	0,995	17500
2	107	111260	103710	43,32	458,4	2,782	0,916	1,87	77,8	961	102749	0,518	0,471	0,983	21300
3	133	123277	110844	63,4	544,3	3,458	1,09	2,37	98,7	1493	109351	0,492	0,449	0,941	26286
4	147	139803	122733	75,5	582,2	3,828	1,16	2,662	111	1828	120905	0,493	0,43	0,923	29045
5	153	157831	13700	81,0	594,4	3,98	1,19	2,8	116	1982	135018	0,4936	0,425	0,919	30264
6	162	174356	148890	89,23	610,5	4,2	1,221	2,98	124	2216	146674	0,494	0,412	0,906	32048
7	162	193866	165535	89,4	598,2	4,21	1,196	2,014	125,6	2223	163312	0,4944	0,398	0,8924	32068

Заключение

По результатам исследований видно, что подводящее тангенциальное устройство радиальной микротурбины топологически представляет собой граничные условия течения, сочетающие в себе последовательно гидравлические потери местных сопротивлений: внезапное расширение, разворот потока на 90º, поток на радиально-закрученном участке перед рабочим колесом. Формально гидравлически местные потери суммируются через гидравлические прямолинейные участки. В нашем случае потери на местное сопротивление объединены и взаимно влияют друг на друга, что исключает их суммирование в общем случае [14]. Поэтому с точки зрения адекватности результатов предпочтительно пользоваться базой данных по коэффициенту потерь в подводящем устройстве. Сложение потерь возможно только как приближенная оценка.

• 1.    Экспериментальные результаты по коэффициенту потерь Z с о = ( L _вх / R 1 k , h / R 1 k , Re 0 ) и для кольцевого и спирального тангенциальных подводящих устройств представлены в виде базы данных. В общем случае база данных представляет собой табличную функцию от трех переменных:

• 2.    Функция коэффициента потерь достаточно монотонна и не имеет ярких экстремумов, значение функции приблизительно в три раза превышает значение при внезапном расширении потока, что предполагает ее аддитивную структуру.

• 3.    По результатам сравнительного энергетического анализа в первом приближении предложена следующая структура энергетических потерь в тангенциальном подводящем устройстве микротурбины, практически согласующаяся с величиной экспериментальных потерь: ^Z с 0 =^Z вн.расш. ^+Z 9 ₀ o ⁺ ^ рад.уч. , гДе ^ вн.расш. , ^- потери ^на Внезапное расширение; (^ ^- потери на разворот потока на 90°; Z _{рад уч} — потери на трение на радиальном участке канала.

• 4.    Аналогичная база данных получена для коэффициента скорости φ u .

L _вх/ R _{1 k} – относительное плечо входа;

h / R _{1 k} – относительная ширина входного канала;

Re₀ – число Рейнольдса по скорости С ₀( U ₀) в тангенциальном канале.