Энергодинамический вывод уравнений Максвелла

Часто приходится слышать, что в уравнениях электромагнитного поля Максвелла [1] «заключена вся электродинамика». На этом основании из этой теории отбрасывается все то, что не вытекает из этих уравнений. Однако сами эти уравнения до сих пор считаются не выводимыми из каких-либо первичных принципов. Поэтому представляет интерес показать, что в действительности уравнения Максвелла являются следствием энергодинамики [2], обобщающей термодинамику необратимых процессов [3] на процессы полезного преобразования энергии, и описывают лишь весьма частный случай процессов взаимного преобразования электрической и магнитной энергии в замкнутых электрическом и магнитном контурах.

1.    Специфика энергодинамики

Энергодинамика изучает пространственно неоднородные системы с неравномерным распределением по её объему V параметров Θi (энтропии S, массы М, числа молей k-x веществ Nk, заряда З и т.п.). Такие системы могут удаляться от состояния внутреннего равновесия при совершении над системой работы W и самопроизвольно приближаться к нему при релаксации. Это свидетельствует о наличии у таких систем дополнительных степеней свободы и необходимости введения соответствующих им параметров их пространственной неоднородности.

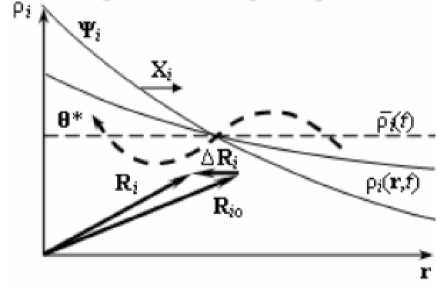
Рис.1. К образованию момента распределения.

Для того, чтобы найти такие координаты, рассмотрим произвольную систему, в которой плотность рi(r,t) = д©//д V любого экстенсивного параметра ©, и сопряженный с ним потенциал Фi(r,t) как функции радиус-вектора r точки поля и времени t распределены по системе так, как указано на рис.1. Как следует из него, при

Р / ^{( t} )

отклонении распределения ©i от равномерного с плотностью некоторое количество этой величины ©i* переносится из одной части системы в другую в направлении, указанном стрелкой. Такое перераспределение носителя г-й формы энергии ©, сопровождается смещением центра R, его величины ©, из первоначального положения Rв текущее. Эти положения определяются известным образом:

R г = © г ⁴ I Р г ( r , t ) Г dV , R io = © г ⁴1 Р / ( t ) Г V. (1)

Отсюда следует, что отклонение системы от однородного состояния сопровождается возникновением «моментов распределения» Z , энергоносителей © , :

Z г = © г A R г = J [ p , ( r , t ) - p ( t ) ] Г dV ,                          (2)

V где AR, = R, — R,„ — вектор смещения центра координаты ©,.

Вследствие этого энергия системы Э становится зависящей не только от параметров ©г, но и от их положения в пространстве. В поляризованных и намагниченных средах, где можно выделить положительные ©i и отрицательные © ’" заряды (или разноименные полюса), рi (t) = 0, а положение их центров Ri и Ri" может быть найдено независимо друг от друга. Поскольку в этом случае AR ’ = — ARi", моменты распределения Z, приобретают особенно четкий физический смысл поляризационных моментов

Z i = Z i + Z ’ " = © i A R i + © i " A R i " = © i " A r i ,         (3)

где A r _i = R _i" - R _i' - усредненное плечо электрического или магнитного диполя. Как показано в [2], в диэлектриках и магнетиках единичного объема такие моменты имеют смысл векторов электрической D и магнитной B индукции.

Благодаря появлению у неоднородной системы дополнительных степеней свободы энергия системы как функция её состояния принимает вид Э = Э (© i-Zi ), так что её полный дифференциал можно представить в форме тождества:

dЭ = S i ф . d © . — S . X _rdZ . ,                           (4)

где ф i = (d Э/ d© i ) — обобщенные потенциалы типа абсолютного давления, температуры, химических потенциалов к -х веществ и т.п.; X i = — (д Э/ d Z i ) — движущие силы процессов переноса, называемые «термодинамическими силами в их энергетическом представлении» [2]; i = 1,2,..., n — число составляющих энергии системы.

Первая сумма этого выражения характеризует изменение энергии рассматриваемой системы Э в результате теплообмена, массообмена, диффузии к —х веществ через границы системы, её электризации и т.п. Вторая же сумма (4) характеризует «техническую» работу dW , совершаемую над такой системой против равновесия в ней.

Нахождение недостающих параметров пространственной неоднородности Z _i и X _i рассматриваемых систем позволяет без каких-либо гипотез и постулатов ввести в энергодинамику понятие времени t , потока смещения J i = d Z i /dt = © i v i какого-либо энергоносителя © i , скорости его переноса v i = d r i / dt , мощности процесса N = dW / dt и т.п., т.е. основные величины, которыми оперирует термодинамика необратимых процессов (ТНП) [3] и многие фундаментальные дисциплины, в том числе энергодинамика . Это позволяет распространить методы ТНП на токонесущие системы, осуществляющие преобразование электрической энергии в магнитную (и наоборот).

2.    Вывод уравнений Максвелла

Приложим теперь основное уравнение энергодинамики (4) к анализу системы, обладающей электрической и магнитной степенью свободы!. Как мыт выяснили, энергия Э такой системы является функцией не только переменных © i , но и параметров неоднородности Z i , которые для системы! единичного объема с энергией Э _v имеют смысл векторов электрической и магнитной индукции D = Р е " Д Г е , B = Р м 'Д Г м , где Р е " = — Р е'; Р м "= — Р м' — плотности соответственно связанных электрических зарядов и так называемых «магнитных масс полюсов» [4]. Соответственно и силы Х , приобретают смысл напряженностей электрического и магнитного полей E и H .

Если считать для простоты все процессы в такой системе обратимыми (бездиссипативными) и исключить из рассмотрения процессы объемной деформации такой системы!, её массообмена с окружающей средой, диффузии в систему каких-либо веществ, ввода в неё электрического заряда и т.д., входящие в 1-ю сумму (4), оно принимает вид, известный еще из классической термодинамики [5]:

- dЭ v = E - d D + H - d B = 0 . (5) Члены правой части этого выражения характеризуют соответственно элементарную работу поляризации dW _;v = E - d D и намагничивания 5W m v = H - d B единицы объема электромагнитной системы. Когда в такой системе осуществляются процессы взаимного превращения энергии электрического и магнитного поля, то их мощности N е = E - d D /dt и N м = H - d B / dt согласно (5) равны по величине и противоположны по знаку. Это непосредственно приводит к соотношению вида:

E - ( d D /dt ) = - H - ( d B / dt ). (6)

Этим простым соотношениям можно придать вид уравнений Максвелла, если рассмотреть систему, состоящую из замкнутого электрического контура произвольной длины I _e и переменного (в общем случае) сечения f_e , который в свою очередь охватывает замкнутый магнитопровод длиной I _м с переменным по длине сечением f_M . Примером такой системы является обычный трансформатор с сердечником. Учитывая непостоянство f_e и f_№ , перейдем к интегральной форме соотношения (6):

N е = J E - ( d D / dt ) dV _e; N м = J H - ( d B / dt ) dV м , (7)

Элементы dVe и dVм объемов Ve и Vм, занятых проводником и магнетиком, можно представить в виде произведения ортогональных векторных элементов соответственно длины и сечения электрического контура и магнитопровода: dVe = dℓe∙dfe и dVм = dℓм∙dfм. Тогда выражения (7) можно переписать в виде:

N е = ∫∫ E ⋅ ( d D / dt ) ⋅ d ℓ e ⋅ d f e = ∫∫( E ⋅ d ℓ e ) ⋅ ( d D / dt ) ⋅ d f e ;            ( 8)

N м = ∫∫ H ⋅ ( d B / dt ) ⋅ d ℓ м ⋅ d f м = ∫∫( H ⋅ d ℓ м ) ⋅ ( d B / dt ) ⋅ d f м .           (9)

Если принять, что E и H остаются неизменными по сечению соответственно проводника и магнитопровода по всей их длине ℓ _e и ℓ _м, т.е. не зависят от f _e и f _м , то выражение ( E ⋅ d ℓ _e) и ( H ⋅ d ℓ _м) можно вынести за знак интеграла по d f _e и d f _м, переписав выражения (8) и (9) в терминах неравновесной термодинамики [3] следующим образом:

N е = ∫ E ⋅ d ℓ e ∫ ( d D / dt ) d f e = X e J e ;                         (10)

N м = ∫ H ⋅ d ℓ м ∫ ( d B / dt ) d f м = X м J м ,                      (11)

где J _e = ∫( d D / dt ) d f _e, J _м = ∫( d B / dt ) d f _м – скалярные электрический и магнитный потоки смещения, называемые в электродинамике

«потоками сцепления» и традиционно представляемые числом силовых линий, «пронизывающих» сечение соответственно электрического контура и магнитопровода [6]; X _e = ∫ E ⋅ d ℓ _e, X _м = ∫

H ⋅ d ℓ _м – модули так называемых электродвижущей и магнитодвижущей силы (ЭДС и МДС), определяемые циркуляцией соответственно векторов E и H вдоль замкнутых электрического и магнитного контуров [6].

Теперь уравнениям электромагнитного поля можно придать форму, принятую в термодинамике необратимых процессов (ТНП)

[3, 7]:

J e = L ee X e + L eм X м ;

J м = L мe X e + L мм X м .

Эти кинетические уравнения, «феноменологическими законами»,

(13) называемые в ТНП отражают взаимосвязь

электрических и магнитных явлений, вытекающую из равенства (6).

При этом их диагональные члены Lee Xe и LммXм характеризуют явления электропроводности и «магнитопроводности», которые возникают под действием одноименных сил; перекрестные же члены LeмXм и LмeXe связаны с преодолением «чужеродных» сил. Эти силы и вызывают превращение электрической энергии в магнитную и наоборот. Таким образом, явления, происходящие в рассматриваемой системе, вполне адекватно описываются в терминах теории необратимых процессов. Это становится окончательно ясным после доказательства справедливости для рассматриваемой системы соотношений взаимности. Поскольку Nе = – Nм, соотношениям (10) – (11) можно придать более простой вид:

J e / X м = – J м / X e .

Сопоставляя это уравнение с феноменологическими законами

(12) и (13), находим, что левая часть (14) определяет коэффициент Leм, а правая – коэффициент Lмe. Отсюда следуют известные соотношения взаимности Онсагера-Казимира [7]:

L eм ^{= –} L мe ^.

То обстоятельство, что эти соотношения вытекают из закона сохранения энергии, лишний раз указывает на то, что электричество и магнетизм – два независимых явления, поскольку взаимосвязь между потоками Je и Jм возникает только в динамике (Je, Jм ≠ 0). Что касается величины и «размерности» этих коэффициентов, то они зависят от выбранной системы единиц. В системе СИ Lem = – Lme = 1, и с учетом этого вместо (12) можно написать:

X e = – ∫( d B / dt ) d f м , (16)

X м = ∫( d D / dt ) d f e ,

Перейдем на основании теоремы Стокса в выражениях силы Xe= ∫E⋅dℓe от криволинейного интеграла по замкнутому электрическому контуру длиной ℓe к интегралу ∫rot Е⋅dfм по сечению магнитопровода fм. Подобным же образом перейдем в выражении силы Xм= ∫H⋅dℓм от криволинейного интеграла по замкнутому магнитному контуру длиной ℓм к интегралу ∫rot H⋅dfe по поверхности fе, натянутой на электрический контур. Тогда вместо (16) и (17) можем написать:

∫rot Е ⋅ d f м = – ∫( d B / dt ) d f м , (18)

∫rot H ⋅ d f e = ∫( d D / dt ) d f e ;                            (19)

или в дифференциальной форме:

rot H = d D / dt ,                                 (20)

rot E = – d B / dt. . (21)

Эти уравнения отличаются от соответствующих уравнений Максвелла в одном, но чрезвычайно важном отношении: в них фигурируют полные производные по времени от векторов электрической и магнитной индукции dD/dt и dB/dt. Последнее не удивительно, т.к. в исходные уравнения энергодинамики (4) также входят полные дифференциалы векторов поляризации и намагничивания D и B. Характерно, что и сам Максвелл первоначально записывал свои уравнения через полные производные от этих параметров [1,6].

Этим уравнениям можно придать более привычный вид, предложенный Хэвисайдом и Герцем, если в выражениях полной производной электрической и магнитной индукции D — D(r,t) и В = B(r,t) по времени dD/dt = (dD/d t)r + (vе•V)D                       (22)

d B /dt = (d B /d t ) r + ( v _M- V ) B                          (23)

пренебречь «конвективными» составляющими потоков связанных зарядов и полюсов, т.е. принять dB/dt = (dB/dt)r и dD/dt = (dD/dt)r + jе, учитывая тем самым только ток проводимости jе = (vе•V)D — pеvе. Тогда уравнения (22), (23) примут вид rot E — - (dB/dt),                                 (24)

rot H — j е + (d D /д t ) .                               (25)

В этом виде эти уравнения и применяют в электродинамике [2]. Между тем никаких оснований исключать в общем случае из рассмотрения потоки смещения связанных зарядов ре', ре" и полюсов рм', рм" нет, поскольку мы с самого начала рассматривали токонесущую систему, а не абстрактное электромагнитное поле. Если же в соотношениях (22) и (23) учесть потоки смещения связанных зарядов и полюсов, они примут вид dD/dt = (dD/dt)r + jе + jе' + jе " ,                      (26)

d B / dt = (d B /d t ) r + j м' + j м " ,                         (27)

где j е ' — Р е 'У е ' , j е " — Р е " V е ' " j м '= Р м 'V м', j м "= Р м ' У м " • Поскольку в этих выражениях противоположны не только заряды, но и скорости, токи смещения j _е' и j _е " , а также j _м' и j _м " не только не компенсируются, а, напротив, складываются, в токонесущих системах возникают конвективные потоки смещения связанных зарядов j _е k — j _е' + j _е " и полюсов j _м k = j _м ^, + j _м " , так что уравнения (24) и (25) принимают вид [8]:

rot E — j м ^k - (d B /d t ),                               (28)

rot H — j е + j е ^k + (d D /д t ) .                           (29)

Эти уравнения еще более подчеркивают симметрию уравнений Максвелла, поскольку как jе + jеk , так и jмk можно считать полным потоком смещения в диэлектрике и магнетике. С учетом появления в процессах поляризации и намагничивания связанных зарядов и полюсов видоизменяется и другая пара уравнений Максвелла:

div D = Р е + Р е' + Р е " ,                               (30)

diV B = р м ' + р м " ,                                  (31)

если только связанные заряды р е ', р е " и магнитные массы полюсов р м ', р_м " взаимно не компенсируются, т.е. ре' + р е " ф 0 и р_м ' + р_м " ф 0. Это происходит, например, при неоднородной поляризации в связи с возникновением так называемого «поляризационного» заряда [9] или его магнитного аналога, а также в том случае, когда заряды или полюса одного знака смещаются за границы системы [4]. В электромагнитном поле, где такие заряды или полюса отсутствуют, уравнения (30) и (31) сохраняют свой классический вид div D = ρ_е и div B = 0. Однако в этом поле отсутствуют и свободные заряды ρ_е, так что отнесение уравнений Максвелла к полю не вполне адекватно существу дела.

3.    Обсуждение результатов

Явный учет конвективных потоков смещения j _е k и j _м ^k в уравнениях Максвелла для вещества устраняет ряд трудностей электродинамики, в частности, те из них, что связаны с известными исключениями из правила потока [4]. Действительно, согласно (16) и (17) электродвижущая и магнитодвижущая силы возникают не только вследствие изменения векторов электрической и магнитной индукции D и B , но и наличия потоков энергоносителя, независимо от того, чем эти потоки вызваны – перераспределением зарядов по системе или движением самой системы. Это объясняет, почему ЭДС возникает там, где поле B не меняется (∂ B /∂t = 0), и не возникает там, где ∂ B /∂t ≠ 0 (см. примеры с потоком сквозь вращающийся диск и при повороте пластинок, приведенные в [4]. Благодаря этому исключается отмеченная Р.Фейнманом необходимость использования различных законов силы для случая движущегося контура и меняющегося поля.

Далее, учет в уравнениях поля конвективных потоков смещения в их общефизическом понимании легко объясняет факт появления электрической поляризации в движущемся магнетике в отсутствие внешнего поля H . Отличие от нуля производной d D /dt обусловлено в данном случае наличием конвективной составляющей тока смещения j _е ^к , связанной с движением самого электризованного тела. С этих позиций возникновение магнитного поля при движении поляризованного диэлектрика (эффекты

Роуланда – Эйхенвальда и Рентгена - Эйхенвальда), а также поляризация диэлектрической пластины при ее движении в магнитном поле (эффект Вильсона – Барнета) [6] также объясняются как следствие j _е ^к , не требуя привлечения соображений релятивистского характера. В частности, становится ясным, что даже в однородно поляризованных телах при наличии «конвективной» составляющей j _е k разнонаправленные потоки смещения j _е ', j _е" и j _M ', j_M" становятся различными по величине. Это обстоятельство может иметь прямое отношение к явлению «самоускорения» ферромагнетиков после начального толчка (эффекту Сёрла) [8].

Наконец, предложенный здесь термодинамический вывод уравнений электромагнитного поля обнажает ряд допущений, заложенных в их основание. Прежде всего, электродвижущая и магнитодвижущая силы определялись в (16) и (17) для замкнутых электрических и магнитных цепей. Следовательно, уравнения Максвелла не применимы к незамкнутым электрическим токам и элементам тока. Это подчеркивалось и самим Максвеллом. Во-вторых, исключались из рассмотрения неизбежные джоулевы потери, имеющие место в процессе не только электропроводности, но и переполяризации диэлектриков, а также перемагничивания магнитопровода, которые нарушают условия (6) и соотношения взаимности (15). В-третьих, предполагалось, что плотность электрического и магнитного потоков смещения j _е и j _м одинакова по сечению окна магнитопровода и обмотки, а баланс мощностей N е — - N _м соблюдается не только для системы в целом, но и для каждой локальной области рассматриваемой системы, поскольку в противном случае переход к дифференциальной форме (20) и (21) становится некорректным.

Подводя итог, заметим, что предпринятый вывод уравнений Максвелла опровергает расхожее мнение об их «невыводимости» из каких-либо первичных принципов [9]. Далее, он показывает, что уравнения Максвелла описывают процессы в токонесущих системах, а не в свободном пространстве (электромагнитном поле), как это принято считать. Более того, согласно ТНП взаимосвязь потоков смещения (24) и (25) возникает только тогда, когда они имеют один и тот же тензорный ранг и вид (т.е. подчиняются одному из основополагающих требований ТНП –– принципу Кюри [7]). В данном случае это обеспечивается вихревым характером как магнитного, так и электрического поля (циркуляцией векторов Е и Н по замкнутым контурам и наличием rotЕ и rotН). Следовательно, эти уравнения не являются едиными для любых конструктивных разновидностей электротехнических устройств. Наконец, эти уравнения основаны на ряде допущений и не свободны от внутренних противоречий, поскольку наличие тока проводимости не совместимо с допущением обратимости процесса взаимопревращения электрической и магнитной энергии. Все это говорит о том, что в уравнениях Максвелла заключена отнюдь не вся электродинамика. Последнее делает необходимым анализ электромагнитных явлений с более общих позиций единой теории процессов переноса и преобразования любых форм энергии, каковой является энергодинамика [2].