Энергоэффективные индукторы магнитогидродинамических устройств металлургического назначения

В металлургическом производстве для перекачивания, дозирования и перемешивания жидких металлов и сплавов широко применяются плоские линейные индукционные машины, оснащенные трехфазными ( m = 3) и двухфазными ( m = 2) обмотками [1–3].

Особенности использования линейных индукционных машин в металлургии обусловлены большими зазорами между индуктором и жидким металлом. Это требует применения многовитковых обмоток, которые необходимо укладывать активными сторонами в глубокие и широкие пазы индуктора. В таких условиях создание традиционных обмоток с многочисленными изгибами лобовых частей в различных плоскостях становится затруднительным. Особенно сложно изготавливать подобные обмотки для низких частот. Под воздействием электромагнитных сил такая обмотка может деформироваться, что приводит к перетиранию изоляции и выходу ее из строя.

Чтобы преодолеть эти трудности, были разработаны новые типы обмоток, катушки которых отличаются простотой изготовления и повышенной надежностью в эксплуатации. Эти обмотки состоят из концентрических катушек, проводники которых изгибаются на широкую сторону поперечного сечения катушки.

Существующие технические решения

В работе [1] представлен индуктор линейной индукционной машины, который включает в себя разомкнутый магнитопровод с двухфазной обмоткой и воздушным охлаждением. Фазы обмотки образованы одинаковыми плоскими катушками, разделенными на несколько секций по высоте паза. Секции катушек разных фаз расположены в разных пазах и чередуются по высоте. Такая конструкция обмотки способствует образованию продольных каналов для естественного охлаждения и позволяет сократить расход обмоточных материалов, исключая перекрещивание лобовых частей. Однако у этого устройства есть два существенных недостатка: большие поперечные габариты, обусловленные вылетом лобовых частей, и отсутствие компенсирующих элементов, которые могли бы уменьшить вредное воздействие пульсирующего магнитного потока, возникающего из-за разомкнутости магнитопровода. Известны трехфазные и двухфазные обмотки индукторов линейной индукционной машины, выполненные из концентрических катушек плоской прямоугольной формы, которые расположены на стержнях магнитопровода. В работе [2] предложена линейная индукционная машина с трехфазной обмоткой, фазы которой образованы одинаковыми концентрическими катушками плоской формы, разделенными на несколько секций. Секции катушек расположены на стержнях магнитопровода, что создает каналы для естественного или принудительного воздушного охлаждения. Такая конструкция позволяет устройству перекачивать или перемешивать высокотемпературные жидкие металлы. В работе [3] описана индукционная машина с двухфазной обмоткой, выполненной из одинаковых концентрических катушек, расположенных на стержнях магнитопровода. Секции катушек одной фазы находятся на первом и третьем стержнях, а секции другой фазы – на втором и четвертом.

Однако как трехфазная, так и двухфазная обмотки из плоских концентрических катушек, расположенных на стержнях магнитопроводов, имеют относительно низкие обмоточные коэффициенты [4, 5]. Это приводит к тому, что индукторы линейных индукционных машин с такими обмотками обладают невысокими энергетическими и электромагнитными свойствами.

Следует отметить, что индукторы с разомкнутым магнитопроводом создают в активной зоне не только бегущее, но и пульсирующее магнитное поле. Эти пульсирующие поля индуцируют токи во вторичной среде (жидком металле), что приводит к дополнительным потерям мощности и увеличению несимметричной нагрузки фаз. Для подавления или компенсации пульсирующего магнитного поля было предложено выполнить обмотку линейной индукционной машины с наличием на концах индуктора компенсирующих элементов, которые создают необходимую намагничивающую силу для компенсации пульсирующего магнитного поля.

В работе [4] представлена трехфазная обмотка линейной индукционной машины с фазной зоной 60° (электрических) и расположением катушечных групп в двух плоскостях. Особенностью обмотки является наличие за пределами активной зоны компенсирующих элементов, электрические токи которых способны компенсировать вредное влияние пульсирующего маг-– 1037 – нитного потока. Роль компенсирующих элементов играют свободные стороны катушек, расположенные вне активной зоны. Также в работе [4] описана индукционная машина с двухфазной двухплоскостной обмоткой, особенностью которой является намотка в «развалку», то есть катушечные стороны делятся пополам, и лобовые части этих половинок отгибаются в разные стороны. Такая обмотка имеет хороший обмоточный коэффициент и меньший поперечный размер индуктора за счет меньшего вылета лобовых частей. По эффективности работы и электромагнитным свойствам трех- и двухфазные обмотки мало отличаются друг от друга [6]. Однако недостатком упомянутых трехфазной и двухфазной двухслойных обмоток линейных индукционных машин (ЛИМ) является различие индуктивных сопротивлений катушек, расположенных в нижнем и верхнем слоях. Это приводит к несимметрии токов в фазах и ухудшает условия охлаждения.

В работе [7] предложен индуктор линейной индукционной машины, имеющий часть пазов в активной зоне и два паза, расположенных вне активной зоны на краях индуктора. Каждая секция обмотки содержит два слоя катушек. К недостаткам этого индуктора следует отнести большие продольные размеры из-за большого количества пазов и низкий обмоточный коэффициент, что, в свою очередь, снижает энергоэффективность.

Целью данной работы было создание индуктора линейной индукционной машины для транспортировки, дозирования и перемешивания жидких металлов с меньшими массогабаритными и улучшенными энергетическими показателями.

Постановка задачи моделирования

Рассмотрим индуктор длиной X = 2 т (р = 1), который установлен на расстоянии 3 от жидкого металла, как показано на рис. 1. При выборе длины индуктора X и других его параметров, таких как количество пазов K и ширина паза 2Δ, необходимо учитывать расположение индуктора относительно ванны с жидким металлом. Для эффективного магнитогидродинамического (МГД) перемешивания расплава металла должно выполняться следующее условие [4]:

Т > 3 3 , (1)

где 3 - расстояние индуктора от жидкого металла.

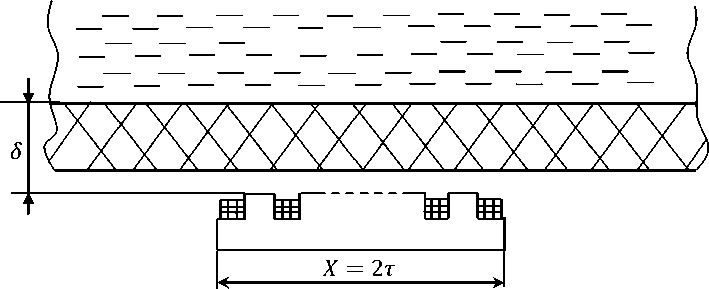
Рис. 1. Система «индуктор линейной индукционной машины – расплав»

Fig. 1. The system “inductor of a linear induction machine – melt”

На рис. 2а и 3а представлены известные индукторы ЛИМ с трехфазной (при K = 8, длине индуктора X = 30Δ, относительной длине индуктора X = 30, сдвиг фаз между токами компенсирующих элементов α ₈ = –180°) и двухфазной ( K = 6, длине индуктора Х=20 Δ , относительной

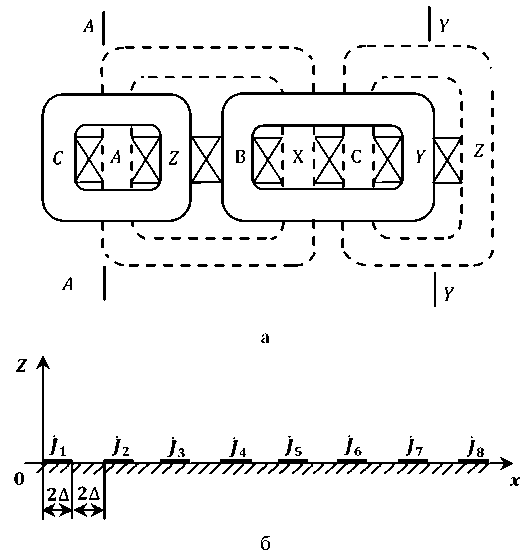
Рис. 2. Индуктор ЛИМ с трехфазной обмоткой с компенсирующими элементами

• Fig. 2.    LIM inductor with three-phase winding with compensating elements

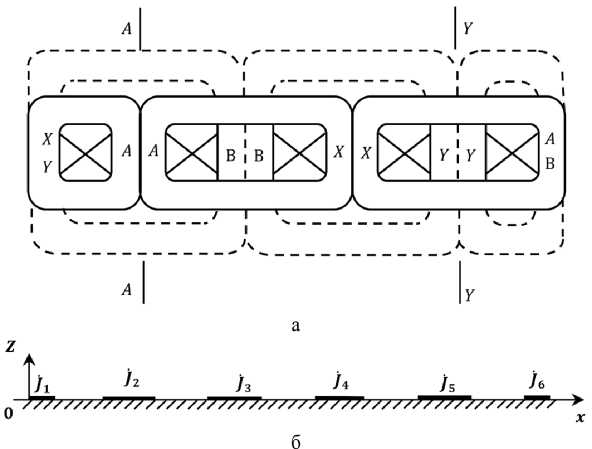
Рис. 3. Индуктор ЛИМ с двухфазной обмоткой с компенсирующими элементами

• Fig. 3.    LIM inductor with two-phase winding with compensating elements

длине X = 20, α ₆ = –180°) концентрическими обмотками, которые имеют двухплоскостные лобовые части [7].

Длина индуктора для m -фазной обмотки ( m = 2,3) равна

X = 2Δ(2 K – (4 – m )] = 2 τ ,

или при знаке равенства в (1) получим, что

2Δ[2 K – (4 – m )] = 6 δ

Тогда число пазов индуктора K при заданной ширине паза 2Δ или величина 2Δ при заданном числе пазов K определяются соответственно как

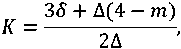
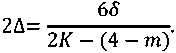
Трехфазная обмотка характеризуется шириной фазной зоны, равной 60° (электрических градусов). Это означает, что электрические токи в соседних пазах активной зоны смещены относительно друг друга по фазе на 60 градусов. Начальные фазы токов в пазах можно увидеть на векторной диаграмме (рис. 4а). Двухфазная обмотка отличается шириной фазной зоны в 90°, а начальные фазы токов в её пазах также представлены на векторной диаграмме (рис. 4б).

Электромагнитное поле, электромагнитные силы и мощности индуктора определяются линейной токовой нагрузкой J ( x ). На рис. 2б и 3б показаны расчетные модели индукторов с трехфазной и двухфазной обмотками соответственно. В трехфазной модели для упрощения принято считать, что ширина всех пазов равна ширине зубцов и составляет 2Δ. В двухфазной модели ширина крайних пазов принимается равной Δ. В обеих моделях каждый k -ый паз представлен поверхностным слоем с комплексной линейной плотностью тока [6]:

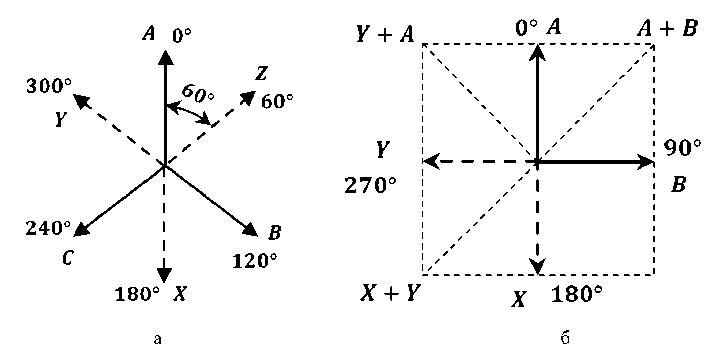
Рис. 4. Начальные фазы токов в пазах

Fig. 4. Initial phases of currents in the slots

j_k=J_keⁱ⁴\                                                    (6)

где Ψ k – начальная фаза тока в k -ом пазу, а

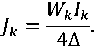
Здесь W_k и I_k – число витков и действующее значение тока в проводниках k -ого паза.

Линейную токовую нагрузку J(x) можно представить в виде ряда Фурье с комплексными коэффициентами [6]. Тогда комплексный коэффициент первой гармоники в этом ряду будет равен xк

Ji = V JMe } x дх= У —sin (—I e l(p^,(8)

X J                   n \ X )

где фаза переменного тока в k -ом пазу:

x_k и Ψ _k – координата центра и начальная фаза тока в проводниках k -ого паза.

Анализ результатов

Если принять линейную плотность тока во всех пазах одинаковой Jk = J , то модуль этого коэффициента можно представить в виде

J ₁ = J · k _об1                                                                         (10)

Об эффективности индуктора можно судить по обмоточному коэффициенту первой гармоники:

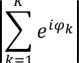
2 /2ттД\ ',"=;slnM

В соответствии с расчетной моделью индуктора, представленной на рис. 2б, определим значение обмоточного коэффициента k об1 для известного индуктора с трехфазной обмоткой. В табл. 1 указаны значения x_k , Ψ _k , и φ_k для каждого k -го паза, которые входят в формулу (9). В пазах с k = 1 и k = 8 размещены компенсирующие элементы, а в пазах с номерами k = 2..7 находятся токи активной зоны.

На рис. 5а изображены комплексные векторы линейной плотности тока jk в пазах, соответствующие расчетной модели индуктора, представленной на рис. 2б. Из рисунка видно, что

Таблица 1

Table 1

k	1	2	3	4	5	6	7	8
Ψ k	240°	0°	60°	120°	180°	240°	300°	60°
x k	Δ	5Δ	9Δ	13Δ	17Δ	21Δ	25Δ	29Δ
φ k	132°	60°	48°	36°	24°	12°	0°	288°

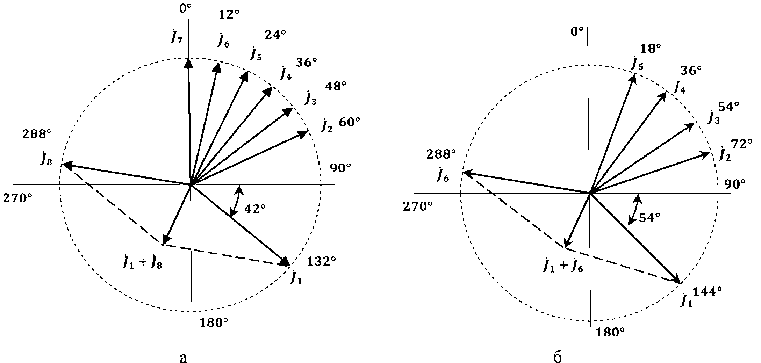
Рис. 5. Комплексные векторы линейной плотности тока в пазах

Fig. 5. Complex vectors of linear current density in slots между векторами токов в пазах активной части существует фазовый сдвиг в 12 градусов. Кроме того, вектор суммы токов компенсирующих элементов j1 + j8 направлен против суммы токов активной части. Значение kоб1, определенное по формуле (11), составляет 0.689.

Аналогично для индуктора с двухфазной обмоткой в табл. 2 для каждого k -го паза указаны значения x_k , Ψ _k , и φ_k , входящие в формулу (9). Относительная длина этого индуктора составляет X = 20. На рис. 5б показаны комплексные векторы линейной плотности тока jk в пазах, соответствующие расчетной модели, представленной на рис. 3б. Между векторами токов в пазах активной части фазовый сдвиг равен 18 градусов, вектор суммы токов компенсирующих элементов j ₁ + j ₆ также направлен против суммы токов активной части, а значение первого члена ряда Фурье k об1 составляет 0.678.

Уменьшая длину индуктора на величину зубцового деления (4Δ), определим обмоточный коэффициент k об1 для каждого индуктора. Сначала проведем сокращение длины индуктора с трехфазной обмоткой. Так, «обрезав» индуктор по линии А-А (рис. 2а), получим индуктор с числом пазов K = 7, с относительной длиной X = 30 – 4 = 26. В крайнем левом полузакрытом пазу расположены проводники фазы A + C = Y (рис. 4а). Сдвиг фаз между токами компенсирующих элементов Y и Z составляет α 7 = –120°. Построив расчетную модель индуктора с K = 7 и определив x_k и Ψ _k для каждого паза, по (11) вычисляем обмоточный коэффициент k _об1 = 0.842.

Таблица 2

Table 2

k	1	2	3	4	5	6
Ψ k	225°	0°	90°	180°	270°	45°
x k	0.5Δ	4Δ	8Δ	12Δ	16Δ	19.5Δ
φ k	144°	72°	54°	36°	18°	288°

Далее, «обрезав» индуктор по линии Y-Y (рис. 2а), получим индуктор с числом пазов K = 6, X = 22, α 6 = –60°, а обмоточный коэффициент k об1 = 0.961.

Аналогично определяем значения k _об1 для индукторов с K = 8, 4, 3. Результаты сведены в табл. 3.

Также уменьшая длину индуктора с двухфазной обмоткой от индуктора с K = 6, X = 20 (рис. 3а) до индуктора с K = 3 и X = 8, получим результаты, приведенные в табл. 4.

Анализируя значения α_k в табл. 2 и 3, можно сделать вывод, что сдвиг фаз между токами компенсирующих элементов в индукторе с K пазами ( K = 8 ÷ 3 для трехфазной обмотки и K = 6 ÷ 3 для двухфазной обмотки) определяется как

360°

a_k = -180° + (2m + 2 - Д')----.

2m

Для примера определим параметры индуктора МГД перемешивателей с трехфазной и двухфазной обмотками, расположенными на расстоянии δ = 450 мм от жидкого металла (рис. 1). Так, для индуктора с трехфазной обмоткой ( m = 3), приняв число пазов K = 6, по (5) находим ширину паза 2Δ = 245 мм. По табл. 3 определяем относительную длину индуктора X = 22. Действительная же длина индуктора X = 2 τ.

В соответствии с рис. 6а для каждого k- го паза определены значения x_k , Ψ _k , и φ_k , результаты сведены в табл. 5. На рис. 6б представлена диаграмма токов в пазах для предлагаемого трехфазного индуктора с числом пазов K = 6, где видно, что векторы стали более коллинеарные, а обмоточный коэффициент k об1 = 0.961.

Таблица 3

Table 3

K	X	α k	k об1
8	30	-180°	0,689
7	26	-120°	0,842
6	22	-60°	0,961
5	18	0°	1,036
4	14	60°	1,019
3	12	60°	0,955

Таблица 4

Table 4

K	X	α k	k об1
6	20	-180°	0,678
5	16	-90°	1,002
4	12	0°	1,230
3	8	90°	1,282

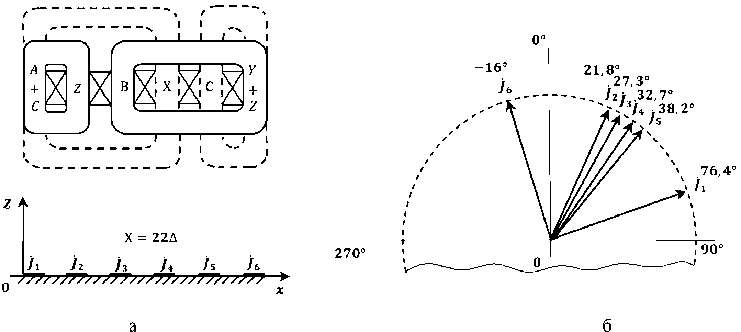
Рис. 6. Укороченный индуктор ЛИМ с трехфазной обмоткой с компенсирующими элементами

Fig. 6. A shortened LIM inductor with a three-phase winding with compensating elements

Таблица 5

Table 5

k	1	2	3	4	5	6
Ψ k	300°	60°	120°	180°	240°	0°
x k	Δ	5Δ	9Δ	13Δ	17Δ	21Δ
φ k	76°	22°	27°	33°	38°	-16°

Аналогично и для индуктора с двухфазной обмоткой ( m = 2), приняв число пазов K = 4, по (5) находим ширину паза 2Δ = 450 мм. По табл. 4 определяем относительную длину индуктора X = 12. Тогда действительная длина индуктора X = 2 τ , условие (1) выполняется.

В соответствии с рис. 7а для каждого k -го паза определены значения x k , Ψ k , и φ k (табл. 6, рис. 7б). Обмоточный коэффициент составил k _об1 = 1.23.

Таблица 6

Table 6

k	1	2	3	4
Ψ k	315°	90°	180°	315°
x k	0.5Δ	4Δ	8Δ	11.5Δ
φ k	60°	30°	60°	30°

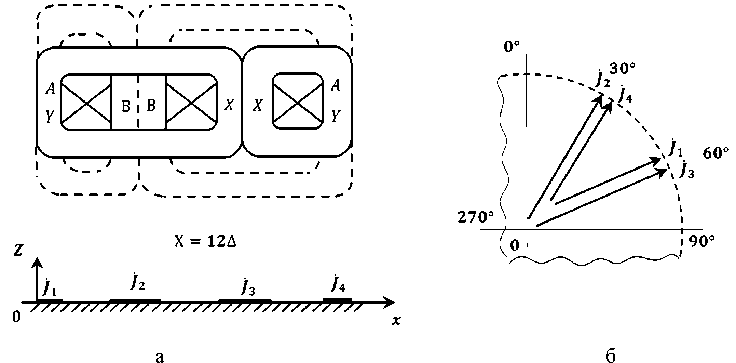
Рис. 7. Укороченный индуктор ЛИМ с двухфазной обмоткой с компенсирующими элементами

Fig. 7. A shortened LIM inductor with a two-phase winding with compensating elements

Выводы

Сравнивая массогабаритные и энергетические характеристики рассматриваемого индуктора с известными, можно сделать следующие выводы.

• 1.    У индуктора с трехфазной обмоткой (рис. 2а) длина составляет X = 30Δ, количество пазов K = 8, а величина обмоточного коэффициента k _об1 = 0.689. Уменьшение длины индуктора с X = 30Δ до X = 22Δ, что составляет 27 %, позволяет повысить энергоэффективность индуктора с k _об1 = 0.689 до k _об1 = 0.962, что составляет около 30 %.

• 2.    У индуктора с двухфазной обмоткой (рис. 3а) длина X = 20Δ, количество пазов K = 6, а величина обмоточного коэффициента k _об1 = 0.678. Уменьшение длины индуктора с X = 20Δ до X = 12Δ, что составляет 40 %, позволяет повысить энергоэффективность индуктора с k об1 = 0.678, до k _об1 = 1.23, что составляет около 45 %.

Таким образом, применение индуктора с числом пазов K и шириной пазов 2Δ, определяемых формулами (4) и (3) соответственно, позволяет не только уменьшить массогабаритные характеристики индуктора линейной индукционной машины, но и повысить его энергоэффективность. Следует отметить, что электромагнитные мощности и силы индуктора пропорциональны квадрату тока. Поскольку обмоточный коэффициент входит в линейную токовую нагрузку (10), его увеличение также приводит к пропорциональному увеличению сил и мощностей.