Энергомассовая модель и оптимизация параметров многоразового электроракетного буксира для доставки полезного груза с орбиты Земли на орбиту Луны и с орбиты Луны на орбиту Земли

Одной из перспективных задач освоения космоса является создание действующих и постепенно расширяемых и модернизируемых лунных комплексов, в т. ч. производственных — с добычей и переработкой полезных ископаемых [1–4]. Рассматривается не только возможность их использования для обеспечения созданной лунной инфраструктуры, в т. ч. обитаемых лунных баз, но и для нужд Земли [5]. Кроме производства, накопления и длительного хранения таких расходных на Луне материалов, как кислород, водород, метан, вода, аргон, ко второй очереди освоения полезных ископаемых относится добыча и использование в производстве железа, титана, кремния, алюминия и других материалов. При этом может рассматриваться использование этих материалов в качестве полуфабрикатов с доставкой их как на окололунные, так и на околоземные орбиты [6]. Особого внимания заслуживает производство на Луне и доставка на Землю экологически чистого термоядерного топлива гелия-3 для наземной термоядерной энергетики [7, 8], учитывая отсутствие на Земле гелия-3 и необходимость постепенной замены атомной энергетики на реакторах деления на термоядерную энергетику [9–11].

В последнее десятилетие возник ещё один мощный стимул промышленного освоения Луны с последующей доставкой добытых материалов на Землю. По прогнозам аналитиков, разведанных на Земле запасов редких и редкоземельных металлов осталось не более чем на 40 лет [12]. До недавнего времени считалось, что лунные ударные кратеры не содержат пород образовавших их астероидов, так как при высоких скоростях падения ударники испаряются в процессе столкновения с поверхностью Луны. Однако благодаря последним исследованиям [13] выяснилось, что при скорости падения меньше 12 км/с ударник может частично сохраниться в механически раздробленном состоянии. Следовательно, к возможным ресурсам, присутствующим на лунной поверхности, можно отнести никель, кобальт, платину и редкие металлы астероидного происхождения. Цена разведанных залежей этих металлов на Луне огромна, и часть прибыли от добычи этих материалов предлагается использовать для создания системы термического режима земной атмосферы с целью парирования превышения допустимого уровня глобальной температуры Земли [14].

Для решения рассмотренных задач освоения Луны в перспективе необходимо создание высокоэкономичных транспортных средств для обеспечения больших грузопотоков не только с Земли на Луну, но и с Луны на Землю.

Вопросы создания грузовой транспортной системы для обеспечения больших грузопотоков с Земли на Луну рассмотрены в ряде работ [1, 15–18], в т. ч. с использованием многоразовых межорбитальных буксиров (ММБ) [15, 16, 19]. Показана высокая эффективность создания ММБ на основе электроракетных транспортных аппаратов (ЭРТА) [20, 21]. Так, в работе [20] было выполнено сравнение эффективности ММБ на основе электроракетной двигательной установки (ЭРДУ) с электропитанием от термоэмиссионной ядерно-энергети-ческой установки (ЯЭУ) электрической мощностью порядка 1 000 кВт [22] с эффективностью одноразовых межорбитальных буксиров (МБ) на основе жидкостных ракетных двигателей (ЖРД). Показано, что при годовом грузопотоке с орбиты Земли на орбиту Луны до 100 т/год [1] при использовании МБ на основе ЖРД потребуется 60–70 пусков ракет-носителей (РН) грузоподъёмностью 20–25 т, а при использовании ММБ на основе ЭРДУ — только 13. Соответственно, удельная стоимость доставки единицы массы полезного груза (ПГ) будет ниже не менее чем в два раза.

Однако в приведённых выше работах анализируется эффективность ММБ на основе ЭРТА лишь для доставки ПГ с орбиты Земли на орбиту Луны — обратный рейс ММБ совершает порожним (без модуля ПГ). В то же время, по крайней мере в отдалённой перспективе, потребуются ММБ для доставки грузов не только с орбиты Земли на орбиту Луны, но и обратно. В настоящей работе сделана попытка оценить возможные и оптимальные параметры такого ММБ.

Постановка задачи исследования

В качестве транспортной задачи обеспечения больших грузопотоков при освоении Луны рассматривается задача обеспечения в одном рейсе «орбита Земли – орбита Луны – орбита Земли» («З–Л–З») доставки полезных грузов (ПГ₁) не только с орбиты Земли на орбиту Луны, но и доставки полезных грузов в обратном перелёте (ПГ₂) — с орбиты Луны на орбиту Земли. В качестве критерия эффективности ММБ рассматривается и транспортировка в одном рейсе «З–Л–З» суммарного полезного груза ПГ _Σ = ПГ₁ + ПГ₂.

концептуальная структурная схема компоновки ММБ и её особенности

Как и в работах [16, 23], будем рассматривать ММБ на основе ядер-ной электроракетной двигательной установки (ЯЭРДУ), включающей ЯЭУ на основе термоэмиссионного реактора-преобразователя (ТРП) [22], ЭРДУ с электроракетными двигателями (ЭРД) типа ДАС (двигатель с анодным слоем) [24, 25] с системой хранения и подачи (СХП) рабочего тела — ксенона.

В качестве опорной орбиты Земли будем рассматривать так называемую радиационно-безопасную орбиту (РБО) высотой не ниже 800 км, а в качестве орбиты Луны — круговую орбиту высотой 100 км.

Так как ресурс ЯЭУ космического назначения по современным представлениям и оценкам существенно выше (5–7 лет) [26], чем ресурс современных ЭРД (порядка одного года [24]), для нивелирования расхождения в ресурсной способности ЯЭУ и ЭРДУ рассматривается конструктивная схема ММБ, при которой осуществляется замена ЭРДУ при каждом последующем рейсе «З–Л–З».

Возможны два варианта вывода ЭРДУ на РБО Земли:

• 1)    замена ЭРДУ в сборе с полностью заправленной топливом СХП при каждом рейсе, т. е. вместе с блоком ПГ на РБО ракетоносителем выводится новая ЭРДУ;

• 2)    замена только блока тяговых модулей с ЭРД перед каждым рейсом, при этом СХП, система управления и другие агрегаты ЭРДУ остаются в составе ММБ.

Однако второй вариант требует дозаправки ЭРДУ топливом на орбите, и имеет два возможных решения:

• 1)    доставка рабочего тела в баках одним пуском в составе блока ПГ;

• 2)    дозаправка МБ на РБО с помощью отдельного танкера или топливной платформы.

Но преимущество выведения одним пуском РН блока (модуля) ПГ, максимально приближенного по массе к пороговому значению выводимой массы для РН, нейтрализуется сложностью создания системы заправки, предполагающей наличие на орбите дополнительного объекта и прилагающейся к нему инфраструктуры для регулярной доставки рабочего тела на орбиту. Этот вариант, возможно, будет рассматриваться на более поздних этапах освоения космоса, когда транспортное сообщение в околоземном космосе будет достаточно развито.

Постоянная замена ЭРДУ по истечении срока службы тяговых модулей ЭРД накладывает особенности компоновки ММБ в части расположения тяговых модулей ЭРД, обеспечивающих эту замену.

Предлагается симметричное размещение тяговых модулей ЭРД в хвостовой части ММБ на расстоянии ~10 м от продольной оси изделия на поворотных устройствах, с направлением истечения реактивной струи ЭРД в сторону, противоположную движению ММБ, а значит в сторону, противоположную расположению ЯЭУ, отсеку с ПГ, приборному отсеку и другим частям ММБ.

Такое расположение тяговых модулей ЭРД, помимо создания маршевой тяги и управляющих моментов по рысканию, тангажу и крену, обеспечивает защиту от разрушающего воздействия реактивных струй плазмы ЭРД на поверхности ЯЭУ, отсека ПГ и других частей ММБ.

При таком размещении более целесообразно заменять весь блок ЭРДУ, чем, оставляя баки и основные агрегаты СХП, при каждом рейсе устанавливать на штангах связки ЭРД.

Таким образом, в рамках данной задачи целесообразно рассматривать вариант двухэтапной схемы развёртывания транспортного комплекса на РБО, который подразумевает конструктивное и функциональное разделение на два выводимых модуля, а также их последовательную доставку с последующей стыковкой на РБО двух следующих модулей ММБ:

• •    первый модуль (основной) , использующийся в течение всего срока эксплуатации ММБ — блок с ЯЭУ, системой охлаждения, системой отведения ЯЭУ, приборно-агрегатным отсеком и стыковочным агрегатом;

• •    второй модуль — ЭРДУ с заправленной СХП и блок ПГ с системой отведения [16].

Так как масса второго модуля может быть меньше или больше, чем масса первого, второй модуль может быть выведен ракетой-носителем меньшей или большей грузоподъёмности соответственно.

Математическая модель ММБ (система уравнений) для определения оптимальных параметров ММБ на основе яэрду

Для решения поставленной задачи требуется определить зависимость массы ПГ1, задавая время перелёта с РБО на низкую опорную орбиту (НОО) Луны.

С учётом перспектив появления новых космических программ по дальнейшему освоению близлежащего космического пространства (в перспективе — освоение ближайшего спутника Земли — Луны) и развития космической техники, создание и эксплуатация сверхтяжёлых космических аппаратов класса ММБ подразумевает осуществление доставки ПГ как с Земли на Луну, так и обратно, иными словами, m _ПГ2 ≠ 0.

В данной статье описывается анализ эффективности сверхтяжёлого космического аппарата класса ММБ, I ₁ ≠ I ₂ и m _ПГ1 ≠ m _ПГ2 ≠ 0 с частным случаем m _ПГ1 = m _ПГ2 ≠ 0, где I ₁ и I ₂ — удельные импульсы ЭРДУ при перелётах «Земля – Луна» и «Луна – Земля» соответственно; m _ПГ1 и m _ПГ2 — масса модуля ПГ при перелётах «Земля–Луна» и «Луна–Земля» соответственно. I ₁ и I ₂ могут быть как равны, так и не равны. Наложение каких-либо ограничений на соотношение удельных импульсов не нарушает причинноследственных связей. Устанавливая в качестве граничных значения удельных импульсов прямого и обратного перелётов, мы фактически влияем лишь на значения массы ПГ, доставляемых при прямых перелётах на НОО Луны и обратных перелётах на РБО Земли, что в рамках исследуемой задачи и требуется.

Для оптимизации характеристик перелёта введём коэффициент, определяющий соотношение масс модулей ПГ на перелётах «Земля–Луна» и «Луна–Земля», kПГ

^m ПГ2

^m ПГ1 ^,

и коэффициент, определяющий соотношение удельных импульсов ЭРДУ при перелётах «Земля–Луна» и «Луна–Земля»,

I k = 2. (2) si

Для начала необходимо задать граничные условия модели перелёта, а именно: ресурс ЯЭУ Т _ЯЭУ и время перелёта «Земля–Луна» Т ₁.

Ресурс ЯЭУ имеет прямое влияние на величину доставляемого ПГ, т. е. существует прямая зависимость М _ПГ от Т _ЯЭУ. По аналогии с работами [16, 23], примем ресурс ЯЭУ в пять лет, что считается вполне обоснованным с учётом современного уровня развития технологий.

Ресурс электроракетных двигателей различных типов может быть разным. В данной работе за основу ЭРДУ был взят тип двигателя ДАС. Ресурс такого двигателя около одного года, что подтверждается экспериментально в работе [24].

Обозначим начальную стартовую массу ММБ, собранного на РБО (перелёт «Земля–Луна»), как m ₀₁. Она определяется как сумма масс всех систем и агрегатов, входящих в состав транспортного комплекса:

m ₀₁ = m _ЯЭУ + m _ЭРД +

m _т + m _СХП +

+ m _СПУ + m _к + m _ПГ1, (3)

где m _ЯЭУ — масса ЯЭУ; m _ЭРД — масса тяговых модулей с ЭРД; m _т — масса топлива (рабочего тела); m _СХП — масса СХП; m _СПУ — масса системы питания и управления; m _к — масса конструкции ММБ, систем и агрегатов отведения ЯЭУ, систем стыковки, но без учёта массы конструкционных элементов отсека ПГ [27]. В формуле (3) учитывается именно масса всего модуля (отсека) ПГ, где, кроме массы самого ПГ, учитывается масса части систем, агрегатов и элементов конструкции, составляющих сам модуль, отделяемый на орбите Луны от ММБ.

Под массой конструкции понимается масса систем отведения и стыковки, других систем и агрегатов, обеспечивающих конструкционную целостность буксира на всех этапах эксплуатации (включая этап выведения на орбиту с помощью РН).

Затраты характеристической скорости для спиральных траекторий при полётах с двигателями малой тяги для перелёта на орбиту Луны Vх1 и обратного перелёта Vх2 без аэродинамического торможения в верхних слоях атмосферы будут равны, т. е. Vх1 = Vх2 = Vх.

В соответствии с работой [16], выражение для удельного импульса следующее:

2 Nэрду^эрду T   Vx m0Vх        2

где N _ЭРДУ — мощность ЭРДУ; η_ЭРДУ — КПД ЭРДУ, η_ЭРДУ = 0,6–0,7 [28]; T — время перелёта между орбитами РБО Земли и НОО Луны; m ₀ — стартовая масса ММБ на орбите; V _х — затраты характеристической скорости на перелёт.

Мощность ЭРДУ напрямую зависит от мощности питающей её ЯЭУ:

N

ЭРДУ

N

ЯЭУ

1 + k СН

где N _ЯЭУ — мощность ЯЭУ; k _СН — коэффициент затрат энергии на собственные нужды ЯЭУ и потери мощности в шинах при передаче энергии от ЯЭУ к ЭРДУ и другие различные потери (обычно k _СН ≈ 0,1).

Следует учесть, что удельный импульс ЭРД — величина, зависящая от параметров двигателя. Следовательно, зависимость удельного импульса от времени перелёта может рассматриваться только для оптимизации параметров ММБ и времени межорбитального перелёта, но не в качестве причинно-следственной связи.

В соответствии с работой [29], эмпирическая зависимость удельной массы ЯЭУ γЯЭУ (кг/кВт) от её электрической мощности (кВт) выглядит следующим образом:

A γ_ЯЭУ =           + D ,

ЯЭУ

где A , B , C , D

коэффициенты

аппроксимации.

В зависимости (6) рассматривался диапазон значений электрической мощности термоэмиссионных ЯЭУ от 10 кВт (ЯЭУ «Топаз») до 550 кВт

(ЯЭУ для МБ «Геркулес»). Для ЯЭУ с выходной электрической мощностью в пределах указанного диапазона коэффициенты в выражении (6) принимают следующие эмпирические значения: A = 51,43 кг; B = 0,01; C = 0,35 кВт; D = 4,85 кг/кВт.

Используя понятие удельной массы, нетрудно определить массу систем ЯЭУ и ЭРДУ через мощность ЯЭУ, которая является одной из основных характеристик рассматриваемых систем. Таким образом, с учётом выражения (5), массу ЯЭУ и массу ЭРДУ можно определить следующим образом:

^m ЯЭУ ^{= γ} ЯЭУ ^N ЯЭУ^;

^m ЭРДУ

^K зап ^ ЭРДУ ^N ЯЭУ

1 + k _СН ^,

где γ_ЯЭУ определяется из зависимости (6); k _зап — коэффициент запаса, k _зап = 1,1; γ_ЭРДУ — удельная масса ЭРДУ.

По аналогии с работами [16, 23], в настоящей модели предлагается оценивать массу конструкций в долевом соотношении от стартовой массы ММБ:

m _к = α m ₀₁, (9)

где α = 0,02…0,05 — эмпирический коэффициент, его значение принято из анализа концептуальных проектов ММБ.

Для рассматриваемой задачи целесообразно разделить массу конструкции на две составляющие:

• •    массу систем, остающихся в составе основного блока ММБ (система отведения ЯЭУ, силовые адаптеры, система стыковки);

• •    массу элементов конструкции, выводимых вместе с ПГ (система отведения блока ПГ, система стыковки, адаптеры и другие элементы).

Оценивать массу элементов конструкции, отделяемых на НОО Луны, m _к2 имеет смысл в виде коэффициентов от полной массы конструкции:

m _к2 = β m _к, (10)

где β = 0,3…0,4 — некий эмпирический коэффициент, характеризующий массу конструкции, отделяемую от ММБ на орбите Луны вместе с модулем ПГ.

Масса рабочего тела рассчитывается из условия, что ММБ не дозаправляется на орбите Луны, т. е. рассматривается вариант, когда после каждого полного рейса «З–Л–З» на ММБ осуществляется полная замена ЭРДУ и СХП с топливом на РБО. При этом предполагается наличие некоторого резерва рабочего тела (топлива), которое будет характеризоваться также некоторым эмпирическим коэффициентом, отражающим процентное соотношение резерва к общей массе рабочего тела, необходимого для перелёта mт = mт1 + mт2 + λ(mт1 + mт2) =

= (1+ λ)( m _т1 + m _т2), (11)

где λ = 0,05…0,10 — коэффициент резерва рабочего тела.

Учитывая зависимость удельного импульса от типа, параметров и конструкционных особенностей ЭРД и потребляемой им мощности, можно утверждать, что если на орбите Луны не будут изменены тип и характеристики ЭРД (например, замена ЭРДУ), то в течение всего рейса «З–Л–З» удельный импульс не изменится, и обратный перелёт к орбите Земли будет происходить с таким же удельным импульсом ЭРДУ, как и прямой — к Луне, т. е. I _ЭРДУ = I ₁ = I ₂.

Однако на величину удельного импульса влияет такой параметр ЭРДУ, как массовый расход топлива. Примем, что такие параметры, как мощность ЭРДУ и ЯЭУ, остаются неизменными на протяжении всего перелёта «З–Л–З».

Тем самым, изменяя коэффициент соотношения удельных импульсов k_si , мы влияем на необходимое количество рабочего тела, требуемого для перелёта «Луна–Земля», и через этот параметр влияем на суммарную массу ПГ за перелёт «З–Л–З» и, как следствие, на суммарную массу ПГ _Σ за весь ресурс ММБ.

Согласно формуле Циолковского, с учётом формулы (2), значения массы рабочего тела, необходимого для перелётов «Земля–Луна» m _т1 и «Луна–Земля» m _т2, запишутся в следующем виде:

m _т1 = m ₀

–V x

– e ^I 1

–Vx mт2 = m02 1 – e ksiI1 ,                       (13)

где m ₀₂ — начальная масса ММБ при старте с НОО Луны.

Начальная масса ММБ при старте с НОО Луны обратно на Землю (перелёт «Луна–Земля» с модулем ПГ2)

m02 = m0 – mПГ1 – mт1 – mк2 + mПГ2.(14)

Подставляя выражения (1) и (10) в уравнение (14), получим m02 = m0 – mт1 – βmк – (1 – kПГ) mПГ1.(15)

Подставляя выражения (1),(9),

(12)–(14) в соотношение (11), получим следующее выражение для массы заправляемого на РБО рабочего тела ЭРДУ:

–V _x    –V _x

m _т = (1 + λ) m ₀

1 – e ^{I 1} e ^{ksiI 1}

–V x αβ 1 – e ^{ksiI 1}

(1 – k _ПГ) m _ПГ1

–V x

1 – e ^{ksiI 1}

Масса СХП определяется в процентах от массы заправляемого рабочего тела mСХП = kСХПmт,                        (17)

где k _СХП — коэффициент, определяющий массу СХП в долях от массы заправляемого рабочего тела. Обычно k _СХП ≈ 0,1 [27].

Массу СПУ можно определить следующим образом:

m _СПУ = γ_СПУ N _ЯЭУ,                     (18)

где  γСПУ = 1 кг/кВт   — коэффициент удельной массы СПУ [23].

Масса полезного груза одного рейса «земля–луна–земля»

Подставив выражения (1), (9), (15–18) в уравнение (3) и осуществив преобразования, получим выражение для массы модуля доставляемого ММБ «Земля–Луна» одного

(отсека) ПГ, за перелёт полного рейса

«З–Л–З», с учётом влияния коэффициента соотношения между доставляемыми грузами:

–V x    –V x

–V x

m

ПГ1

1 - a - (1 + k^ _п)(1 + X) 1 - e ¹ 1 e

СХП

^{k siI 1}

- ap I 1 - e V i

m ₀ – m _ЯЭУ – m _ЭРДУ – m _СПУ

–V x

1 - (1 + k схп )(1 + Ц1 - e V 1 J (1 - k пг )

Так как масса модуля ПГ, доставляемого ММБ за перелёт «Луна–Земля», определяется выражением (1), соответственно, суммарная масса ПГ за полностью совершённый рейс «З–Л–З» с осуществлённой доставкой m _ПГ1 на НОО Луны и m _ПГ2 обратно на РБО Земли запишется следующим образом:

Из соотношения (4) определим время обратного перелёта, подставив стартовую массу ММБ m ₀₂ при отлёте с лунной орбиты:

T =

V x

I _{2     2}

^m 02 ^V х

2N n

ЭРДУ'I ЭРДУ

m _{ПГ Σ} = m _ПГ1 + m _ПГ2

= m _ПГ1 + k _ПГ m _ПГ1 = (1 + k _ПГ) m _ПГ1.

Анализируя выражения (4, 5, 7, 8), можно сказать, что m _ПГ = f ( N _ЯЭУ, T ₁, k_si , k _ПГ).

оптимальное количество рейсов многоразового буксира

Количество полных рейсов «Земля– Луна–Земля» Q , которое может совершить ММБ к Луне и обратно за весь срок его эксплуатации, ограниченный ресурсом его ЯЭУ Т _ЯЭУ, определяется следующим выражением:

Q =

T

ЯЭУ

рейс

Время же одного рейса T _рейс определяется следующим выражением:

T _рейс = T ₁ + T ₂ + T _ст, (22)

где T ₂ — время перелёта «Луна–Земля», T ₂ является функцией от T ₁, так как зависит от удельного импульса ЭРДУ, выраженного через время T ₁; T _ст — время пребывания и выполнения стыковочных операций на орбитах, T _ст = 7…14 сут.

Определим время перелёта ММБ от Луны к Земле T ₂. Сделаем допущение, что мощность ЯЭУ во время обратного перелёта «Луна–Земля» та же, что и во время перелёта «Земля–Луна».

Суммарная масса полезного груза за весь срок эксплуатации ММБ

Выражение для суммарной массы всех модулей ПГ, доставляемых ММБ на орбиту Луны и обратно в течение всего срока эксплуатации, следующее:

M _{ПГ Σ} = Q m _{ПГ Σ} .

Полученные зависимости суммарной массы ПГ M _{ПГ Σ} от мощности ЯЭУ и времени перелётов между РБО Земли и НОО Луны позволяют определять оптимальные параметры ММБ.

результаты исследования и их обсуждение

Исследование зависимости массы модулей ПГ, доставляемых на орбиты Луны и Земли, от коэффициента соотношения масс ПГ и коэффициента соотношения удельных импульсов позволило определить значения главных параметров ММБ, при которых достигается максимум суммарной массы ПГ, достигаемой при транспортировках за весь срок эксплуатации ММБ.

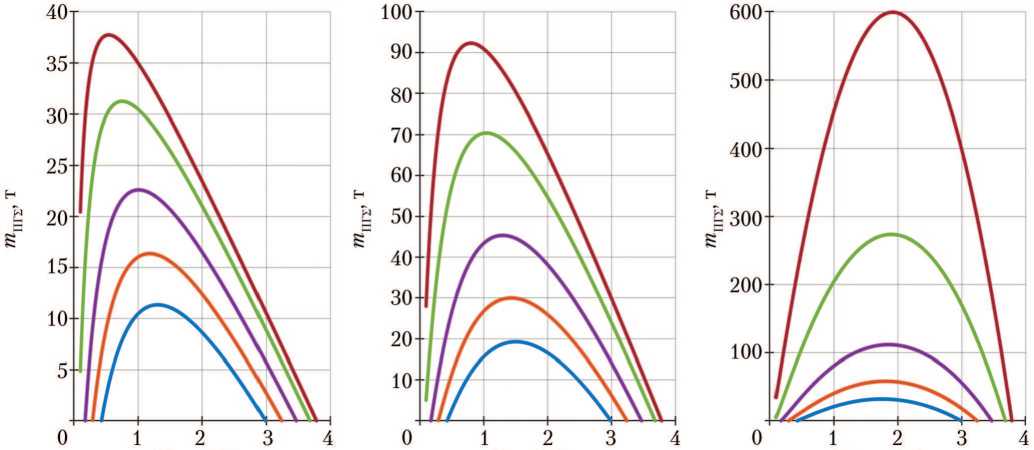
Был рассмотрен диапазон значений стартовой массы ММБ с РБО Земли. По аналогии с работами [16, 23], в качестве иллюстрирующего примера для данной статьи были выбраны следующие характеристики: стартовая масса ММБ на РБО 33 т, ресурс ЯЭУ пять лет. Для указанных характеристик получены зависимости массы ПГ, доставляемого за один рейс (рис. 1), количества рейсов за весь срок (5 лет) эксплуатации ММБ (рис. 2) и суммарной массы ПГ, доставляемого за весь срок эксплуатации ММБ (рис. 3) от мощности ЯЭУ (в качестве параметра принято значение продолжительности перелёта «Земля–Луна» T1 в сутках).

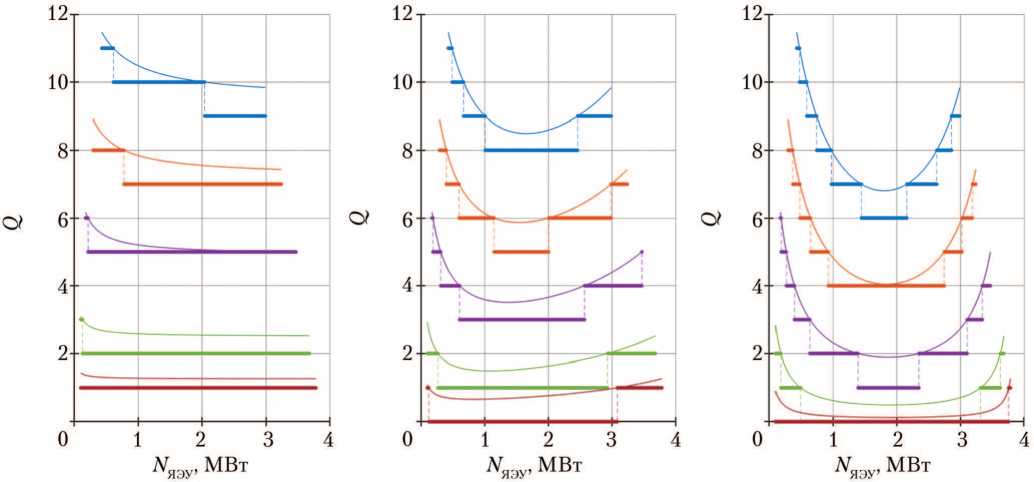
Вследствие дискретности количества рейсов, их зависимость от мощности ЯЭУ является кусочно-линейной. Наличие разрывов в данной зависимости также определяет кусочный характер функции зависимости суммарной массы ПГ, перевозимого за весь срок эксплуатации ММБ (рис. 3).

N , МВт                 N МВт                   N МВт

• а)                                      б)                                       в)

  Рис. 1. Зависимость массы полезного груза m _{ПГ Σ} , доставляемого за рейс «Земля–Луна–Земля», от мощности ядерной энергетической установки N _яэу с ресурсом 5 лет при различных продолжительности перелёта «Земля–Луна» Т ₁ и значениях коэффициента k ПГ : а — k ПГ = 1; б — k ПГ = 5; в — k ПГ ^ ^; — — Т 1 = 60 сут; — — Т 1 = 90 сут; — — Т 1 = 180 сут; — — Т 1 = 360 сут; — — Т 1 = 720 сут (рисунки созданы авторами)

  
  
  

• а) б) в)

Рис. 2. Зависимость количества рейсов «Земля–Луна–Земля» Q от мощности ядерной энергетической установки N _яэу с ресурсом 5 лет при различных продолжительности перелёта «Земля–Луна» Т ₁ и значениях коэффициента k ПГ : а — k ПГ = 1; б — k ПГ = 5; в — k ПГ ^ ^; — — Т 1 = 60 сут; — — Т 1 = 90 сут; — — Т 1 = 180 сут; — — Т 1 = 360 сут; — — Т 1 = 720 сут. Тонкие кривые соответствуют рассчитанным значениям количества рейсов, толстые — его округлённым до целого числа значениям (рисунки созданы авторами)

а)                                      б)                                       в)

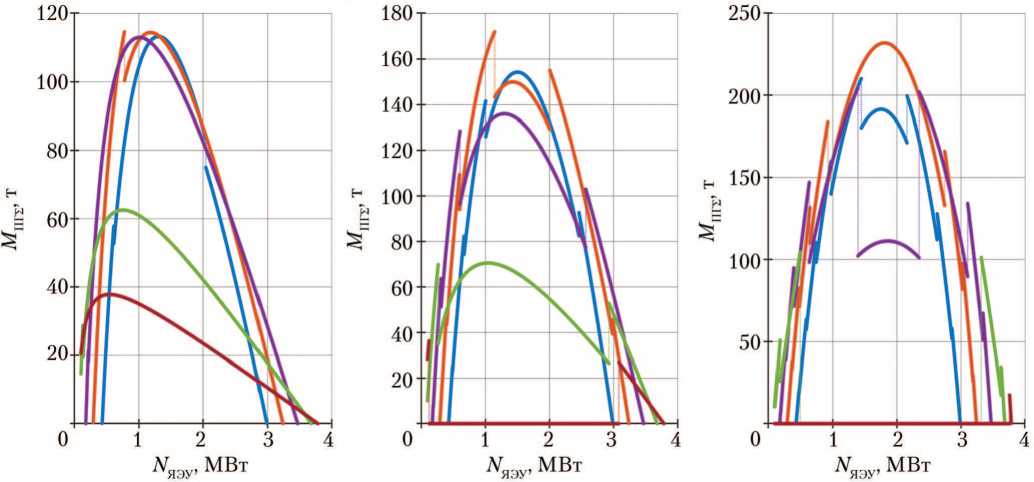
Рис. 3. Зависимость суммарной массы полезного груза М _{ПГ Σ} за весь срок службы многоразового межорбитального буксира от мощности ядерной энергетической установки N _яэу с ресурсом 5 лет при различных продолжительности перелёта «Земля-Луна» Т 1 и значениях коэффициента k ПГ : а — k ПГ = 1; б — k ПГ = 5; в — k ПГ ^ ^; — — Т 1 = 60 сут; — — Т 1 = 90 сут; — — Т 1 = 180 сут; — — Т 1 = 360 сут; — — Т 1 = 720 сут (рисунки созданы авторами)

При создании расчётной программы в среде MatLAB реализовано допущение, что последний рейс «З–Л–З» — полный, т. е. в расчёте учитывались только те случаи, когда существует обязательность возвращения ММБ на РБО Земли из последнего рейса с грузовым модулем ПГ₂.

Так как N _ЯЭУ является одним из основных определяющих параметров m _ПГ, m _ПГ = f ( N _ЯЭУ), то можно сказать, что рис. 3, отражающий зависимость М _{ПГ ∑} от N _ЯЭУ, является графической интерпретацией выражения (24).

Анализ зависимостей суммарной массы ПГ (рис. 3) показывает, что, изменяя время перелёта «Земля–Луна» Т ₁ как граничное значение, можно наблюдать рост этого показателя до определённого значения и его последующее уменьшение, что позволяет говорить о наличии оптимального времени одного рейса, при котором будет осуществлён рейс «З–Л–З» с максимально возможной массой ПГ при заданной стартовой массе и заданном соотношении k _ПГ.

Для ряда значений коэффициента k _ПГ и длительности перелёта Т ₁ от Земли к Луне были получены значения характеристик ММБ (оптимальные мощности ЯЭУ, удельные импульсы перелётов), при которых достигался максимум суммарной массы ПГ M _{ПГ Σ} (рис. 4).

Выделяя максимальное значение для каждого полученного графика и анализируя данные, полученные при k _ПГ → ∞, можно вывести зависимость влияния k _ПГ на M _{ПГ Σ} (рис. 5).

Напомним, что все вышеописанные результаты (рис. 1–5) были получены для частного случая коэффициента соотношения удельных импульсов k_si = 1, т. е. когда удельные импульсы перелётов «Земля–Луна» и «Луна–Земля» равны ( I ₁ = I ₂).

При написании расчётной программы в её алгоритме была заложена возможность варьировать не только N _ЯЭУ, T ₁, k_si , k _ПГ, но и параметр, характеризующий стартовую массу ММБ с РБО Земли m ₀₁.

Окончательные результаты расчётной программы были сведены в таблицу, а их графическая интерпретация представлена на рис. 6.

В таблице приведены численные значения оптимальных параметров ММБ и характеристик транспортной операции «З–Л–З» для двухпусковой схемы формирования на РБО высотой ~800 км электроракетного транспортного комплекса на основе термоэмиссионной ЯЭУ с ресурсом пять лет и ЭРДУ на базе ЭРД типа ДАС с использованием РН грузоподъёмностью 20…25 т.

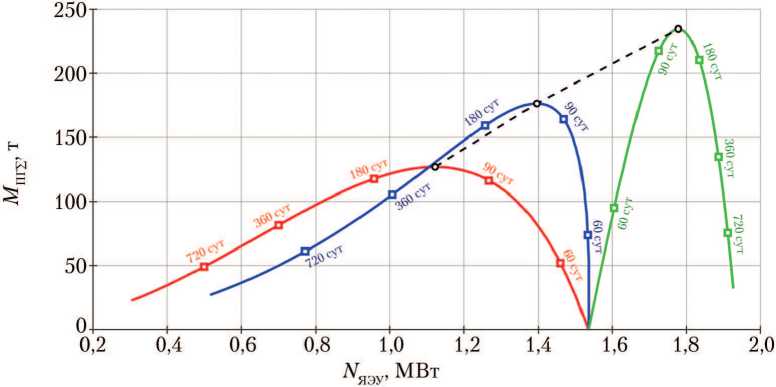
Рис. 4. Зависимость максимальной суммарной массы полезного груза М _ПГΣ и соответствующей ей оптимальной мощности ядерной энергетической установки N _яэу от длительности перелёта «Земля–Луна» Т ₁ при различном значении коэффициента k ПГ : -о-- k n _ПГ = 1; -о-- к _ПГ = 5; -о-- к _ПГ ^ ^; -о-- линия максимумов значений М _ПГ£ (рисунок создан авторами)

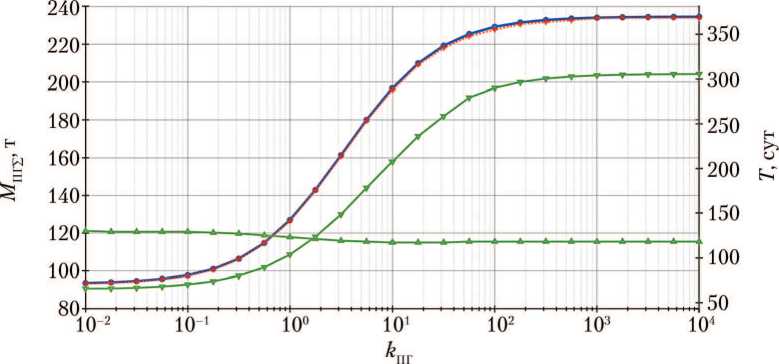
Рис. 5. Зависимость максимальной суммарной массы полезного груза М _{ПГ ∑} , перевозимого многоразовым межорбитальным буксиром по рейсу «Земля–Луна–Земля» за весь срок службы, и времени оптимальных перелётов «Земля-Луна» Т 1 и «Луна-Земля» Т 2 от коэффициента k ПГ : -•- — М _П1Т без учёта целочисленности рейсов; ••«••   — М _{ПГ £} с учётом целочисленности рейсов; ^ — оптимальное время перелёта «Луна-Зе.мля» Т 2 ;

т^ оптимальное время перелёта «Земля-Луна» Т 1 (рисунок создан авторами)

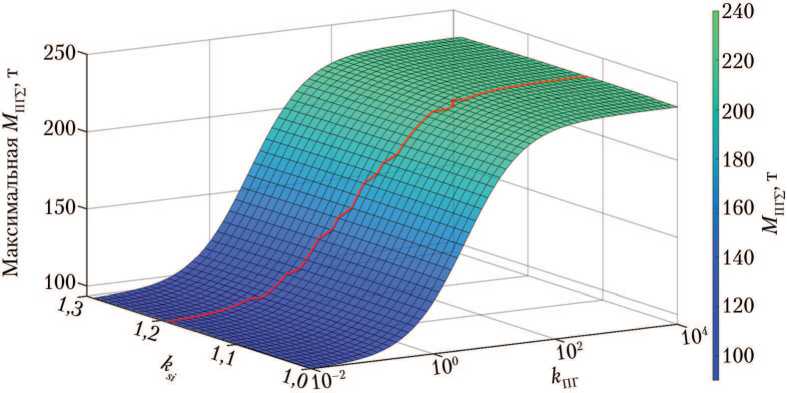
Рис. 6. Зависимость значений максимальной массы полезного груза (ПГ) М _{ПГ ∑} от коэффициента соотношений масс ПГ k _ПГ и коэффициента соотношения удельных импульсов k_si перелётов «Земля–Луна» и «Луна–Земля»:

^— — линия оптимальных максимальных значений М _{ПГ £} опт (рисунок создан авторами)

расчётные значения характеристик и параметров ММБ от соотношения масс ПГ k _ПГ

Параметр ММБ	k ПГ
	0	0,5	1	10	100	∞
Оптимальная мощность ЯЭУ, кВт	933	1 038	1 114	1 512	1 732	1 772
Масса ЯЭУ, кг	9 480	10 010	10 390	12 360	13 440	13 640
Масса ЭРДУ, кг	975	1 085	1 165	1 581	1 811	1 853
Оптимальное соотношение удельных импульсов	1,200	1,175	1,175	1,150	1,125	1,125
Удельный импульс перелёта «З–Л», км/с	44,7	47,8	49,8	62,2	71,2	72,8
Масса РТ, т	8 150	8 600	8 950	10 810	11 850	12 050
Время перелёта «З–Л», сут	120	116	113	106	107	107
Время перелёта «Л–З», сут	72	94	112	217	294	310
Время полного рейса «З–Л–З», сут	206	224	239	337	415	431
Количество рейсов	8,9	8,1	7,7	5,4	4,4	4,2
Масса модуля ПГ при перелёте «З–Л», кг	10 590	9 300	8 350	3 310	520	0
Масса модуля ПГ при перелёте «Л–З», кг	0	4 650	8 350	33 100	51 700	55 500
Суммарная масса модуля ПГ при перелёте «З–Л–З», m ПГ Σ = m ПГ1 + m ПГ2, кг	10 590	13 950	16 690	36 420	52 220	55 500
Суммарная масса ПГ за весь ресурс ММБ, M ПГ Σ , кг	93 850	113 530	127 720	197 430	229 770	235 090
Масса выводимого модуля, m ЭРДУ + m ПГ1 + m т, кг	19 720	18 990	18 460	15 700	14 180	13 900
Остальная часть ММБ, кг	13 280	14 010	14 540	17 300	18 820	19 100

Примечание . Последний столбец таблицы соответствует любому коэффициенту k _ПГ, значение которого k _ПГ → ∞; ММБ — многоразовый межорбитальный буксир; ПГ — полезный груз; ЯЭУ — ядерная энергетическая установка; ЭРДУ — электроракетная двигательная установка; З — Земля; Л — Луна; РТ — рабочее тело.

обобщение и анализ результатов

Рис. 6 и таблица наглядно демонстрируют, что увеличение соотношения масс модулей ПГ (коэффициент k _ПГ) обратного и прямого рейсов приводит к существенному увеличению оптимального значения требуемой мощности ЯЭУ (с ~900 до ~2 000 кВт) с соответствующим увеличением значений массы ЯЭУ и ЭРДУ как систем ММБ. В результате оптимальным будет более длительная транспортировка за счёт увеличения оптимального значения удельного импульса ЭРДУ со снижением количества рейсов за весь ресурс ММБ. Одновременно при заданной начальной массе ММБ на РБО увеличивается и масса заправляемого рабочего тела ЭРДУ при уменьшении массы ПГ₁ перелёта «Земля–Луна». В результате масса ПГ₂ увеличивается как за рейс, так и суммарно за ресурс.

При значениях коэффициента соотношения масс ПГ k _ПГ = 100 и более ( k _ПГ → ∞) максимальная суммарная масса М _{ПГ Σ} за ресурс ЯЭУ стремится к некоему верхнему пределу, при этом масса модуля ПГ₁ стремится к нулю ( m _ПГ1 → 0), то есть условно можно считать, что ММБ летит на опорную орбиту Луны «пустым». Фактически это означает, что ММБ летит без модуля ПГ₁. Из этого можно сделать вывод, что наиболее крупные по суммарной массе грузоперевозки осуществляются в рамках миссий при k _ПГ → ∞, когда ММБ на первой половине рейса (перелёте «Земля–Луна») летит на НОО Луны без груза ( m _ПГ1 = 0), а обратно нагружается модулем ПГ₂ ( m _ПГ2 > 0).

Всё же случаи при kПГ → ∞ не стоит считать самыми выгодными, по крайней мере, на начальных этапах освоения Луны, так как по отношению к грузопотоку на Луну, который будет необходим для создания и организации базы постоянного пребывания на поверхности Луны, её снабжения и прочего ряда различных задач, обратный грузопоток на Землю не будет сопоставим с прямым.

Также есть смысл сделать акцент на том, что численное различие между доставляемым грузом m _ПГ1 при k _ПГ = 0 и m _ПГ2 при k _ПГ → ∞ связано с наложением разного рода ограничений.

Во-первых , это связано с оговорённым ранее наложением ограничения на начальную стартовую массу ММБ с НОО Земли m ₀₁, что, как следствие, устанавливает предел по доставляемой массе m _ПГ1 на перелёте «Земля–Луна».

Во-вторых , в рамках поставленной задачи грузоперевозок отсутствует заданное ограничение на стартовую массу ММБ с НОО Луны m ₀₂. Как было показано ранее, массовые характеристики ММБ и его составляющих зависят от характеристик ЯЭУ (в первую очередь, от её мощности). Тем самым на стартовую массу буксира с НОО Луны m ₀₂ накладывается только требование доставки ПГ₂ на РБО Земли, то есть нужно обеспечить способность ММБ при заданной мощности ЯЭУ на оставшемся запасе рабочего тела осуществлять перелёт «Луна–Земля» с модулем ПГ₂ массой m _ПГ2.

В-третьих , в данной работе не рассматриваются способы выведения модулей ПГ₂ на НОО Луны с её поверхности. Связано это с текущим уровнем развития космических технологий и отсутствием данных по средствам выведения с поверхности Луны, а также с затруднением спрогнозировать, какой по объёму обратный грузопоток нужно будет обеспечивать на первых этапах освоения Луны, какая инфраструктура средств выведения модулей ПГ на НОО Луны будет создана на её поверхности, включая их характеристики и требования, предъявляемые к их эксплуатации.

В-четвёртых, при создании расчётной программы было сделано допущение, что срок эксплуатации ЭРДУ сопоставим со временем полного перелёта «З–Л–З» в силу того, что современные и планируемые в будущем космические миссии при нынешнем уровне развития космических технологий создания и эксплуатации ЭРД постоянно требуют увеличения (непрерывного) времени работы ЭРД (что равноценно увеличению срока эксплуатации), что приводит к медленному, но всё же росту этих показателей среди различных типов ЭРД.

С учётом проведённого и описанного в данной статье исследования и представленных результатов говорить об оптимальном коэффициенте k _ПГ не имеет смысла. Можно лишь говорить о диапазоне максимальных значений M _{ПГ Σ} .

выводы

• 1.    Получена система уравнений для определения оптимальных параметров многоразового межорбитального буксира на основе ЯЭРДУ и характеристик транспортной операции для обеспечения доставки полезных грузов с орбиты Земли на орбиту Луны и с орбиты Луны на орбиту Земли.

• 2.    Применительно к задаче обеспечения грузовых перевозок между орбитами Земли и Луны исследовано влияние соотношения масс полезных грузов между перелётами «Земля– Луна» и «Луна–Земля» на оптимальные параметры ММБ (мощность ЯЭУ, удельный импульс ЭРДУ, время транспортировки, количество рейсов, затраты рабочего тела и др.), которые обеспечивают максимальное значение доставляемого полезного груза за всё время эксплуатации ММБ.

• 3.    Полученные уравнения и алгоритм могут быть использованы для дальнейших оценок оптимальных параметров ММБ на основе ЯЭРДУ, и, при некоторой модернизации, на основе СЭРДУ при решении рассмотренной и других задач в околоземном и близлежащем космическом пространстве, реализующих транспортировку полезных грузов на взаимо-обратных перелётах.

• 4.    Полученные уравнения и алгоритм при некоторой модернизации планируется использовать для исследования влияния на массу доставляемых полезных грузов таких практически важных параметров и условий, как зависимость КПД ЭРДУ от удельного

импульса и рабочего тела, ограничения ресурса и максимального и минимального значений удельного импульса современных ЭРД, целесообразность использования тех или иных типов РН различной грузоподъёмности для выведения энергомодуля и многократной доставки модуля с ПГ и их влияние на суммарную массу ПГ за ресурс ММБ.