Энергосберегающее цифровое управление магнитным приводом в аварийном режиме ориентации спутника
Автор: Сомов Евгений Иванович, Бутырин Сергей Анфимович
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Авиационная и ракетно-космическая техника
Статья в выпуске: 1-1 т.20, 2018 года.
Бесплатный доступ
Представляются алгоритмы экономичного цифрового управления ориентацией информационного спутника в аварийном режиме. Приводятся результаты компьютерной имитации аварийной ориентации спутника землеобзора на солнечно-синхронной орбите.
Космический аппарат, управление ориентацией, аварийный режим
Короткий адрес: https://sciup.org/148205414
IDR: 148205414 | УДК: 629.78
Текст научной статьи Энергосберегающее цифровое управление магнитным приводом в аварийном режиме ориентации спутника
Рассматривается спутник землеобзора на солнечно-синхронной орбите (ССО) высотой от 700 до 1000 км. При возникновении аварийной ситуации в системе управления ориентацией (СУО) космического аппарата (КА), когда ее ресурсы не позволяют выполнить бортовую диагностику состояния и автоматическое восстановление работоспособности с помощью реконфигурации контура управления, формируется команда перехода СУО в энергосберегающий аварийный режим (АР). Рассматриваются вопросы цифрового управления магнитным приводом на всех этапах перехода СУО спутника в аварийный режим и последующего длительного поддержание этого режима, а также результаты исследовании разработанных алгоритмов с помощью компьютерной имитации.
МАТЕМАТИЧЕСКИЕ МОДЕЛИ
Инерциальными системами координат (ИСК), используемыми для описания перемещения центра масс (ЦМ) и углового движения КА, являются геоцентрическая экваториальная система координат (СК) I ⊕ (O ⊕ XIeYeIZIe) и солнечно-эклиптическая СК I s(OsXsIYsIZsI ) .
Сомов Евгений Иванович, начальник отдела навигации, наведения и управления движением НИИ Проблем надежности механических систем СамГТУ.
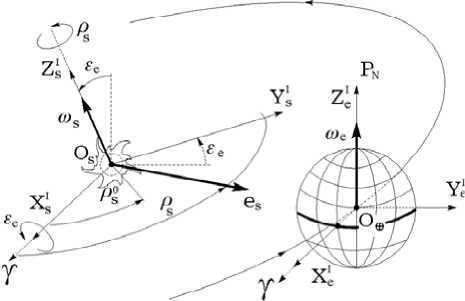
Рис. 1. Инерциальные СК
Начало ИСК I ⊕ расположено в центре Земли O ⊕ , ось X e I направлена в точку весеннего равноденствия ϒ , а ось Z I e – на Северный полюс мира P N по оси суточного вращения Земли с угловой скоростью ω e . Принимается фундаментальная ИСК J2000.0 эпохи To , которая соответствует эпохе фундаментального звездного каталога FK5 для юлианской даты JD (To) = 2451545.0 .
ИСК I s имеет начало в центре Солнца O s , ее ось X s I также направлена в точку ϒ , а оси Y s I и Z s I получаются поворотом соответствующих осей Y e I , Z I e на угол ε e относительно оси X I e (X s I ) . Угол ε e между плоскостями земного экватора X e I O ⊕ Y e I и эклиптики X s I O s Y s I равен 0.41015234 рад (23.44 град), рис. 1. В ИСК I ⊕ орт e s направления из центра Солнца к центру Земли имеет вид e sI( t ) = [ -ε e] 1 [ -ρ s( t )] 3 {1,0,0} , где ρ s ( t ) = ρ s 0 + ω s ( t - t 0 ) , ρ s 0 = ρ s ( t 0 ) , t 0 – некоторый
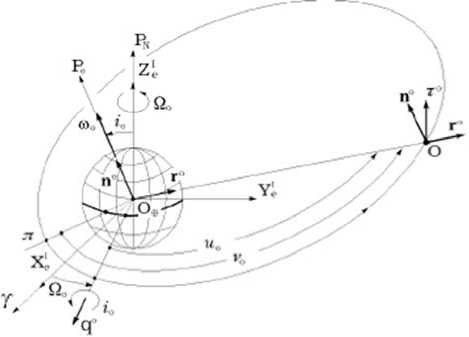
Рис. 2. Орбита КА и орбитальная СК начальный момент времени, ωS=0.19965.10–6 с–1– средняя угловая скорость обращения Земли вокруг Солнца в плоскости эклиптики за тропический год (365.2422 средних солнечных суток). Здесь и далее используются общепринятые обозначения col(⋅) = {⋅} , line(⋅) = [⋅] , 〈⋅ ,⋅〉 ,(⋅)t , [ax] и о ,~ для векторов, матриц и кватернионов, матрицы [α] i элементарного поворота вокруг i-ой оси на угол α, i = 1,2,3 ≡ 1 ÷ 3 , а также Cα ≡ cos α , Sα ≡ sinα . Астрономическая долгота Солнца λs , которая определяется в ИСК I ⊕ как угол между направлением на точку весны ϒ и ортом s = -es направления от центра Земли к центру Солнца, вычисляется по формуле λs(t)=π+ρs(t).
Применяется геодезическая Гринвичская система координат (ГСК) E e (O ⊕ X e Y e Z e ) , связанная с Землей, которая вращается с угловой скоростью ω e = 7.2921158 . 10–5 с–1. Положение ГСК E e относительно ИСК I ⊕ определяется углом ρ e ( t ) = ρ e 0 +ω e ( t - t 0 ) , где
ρe0 = ρe (t0) – угловое положение Гринвичского меридиана относительно направления на точку ϒ при t = t0 и ωe – модуль вектора Ое = {0,0, Юе} угловой скорости вращения Земли. Преобразование векторов-столбцов расположения ro и скорости vo поступательного движения ЦМ O КА из ИСК I⊕ (roI , vIo) в ГСК (rG,vG) выполняется по соотношениям e oo roG = [Pe]3 rO ; VО = -[ОеХ][Ре]3ГО + [Ре]3VО , а обратное преобразование – по соотношениям t = ШзХ; V0 = [Pе]3(v: + [Ое ХЮ.
Плоскость орбиты спутника в ИСК I⊕ определяют долгота восходящего узла ΩO и наклонение iο , рис. 2. Положение ЦМ КА на эллиптической орбите с большой полуосью ao и эксцентриситетом eo определяется вектором ro(t) и истинной аномалией νo(t) , отсчитываемой от перигелия орбиты π, который находит- ся на угловом расстоянии ωπ от ее восходящего узла в направлении движении ЦМ. Истинная аномалия νo (t) связана с аргументом широты орбиты uo(t) соотношением ио(t) = Юп + Vo(t) , см. рис. 2.
Орбитальная система координат (ОСК) O (O x o y o z o) с началом в ЦМ КА O и ортами o 1 , o 2 , o 3 имеет следующие направления осей и связанных с ними ортов: ось O y o и орт o 2 совпадают по направлению с ортом r o вектора r ο ( t ) расположения ЦМ КА в ИСК I ⊕ ; ось O z o и орт o 3 = - n o направлены противоположно орту нормали n o к плоскости орбиты; ось O x o с ортом o 1 дополняет ОСК до правой – принадлежит плоскости орбиты, перпендикулярна оси O y o и направлена в сторону орбитального движения ЦМ КА. Вектор угловой скорости ω o орбитального движения ЦМ КА определяется как Ю = 4( t ) п о =v o ( t ) п о .
Геомагнитная СК M(O⊕XmYmZm ) определяется с помощью вектора магнитного момента M⊕ =M⊕m⊕ магнитного поля Земли (МПЗ) с модулем M⊕ следующим образом: ось O⊕Zm направлена по геомагнитной оси с ортом m⊕ , фиксированным в ГСК, а ось O⊕Xm – по линии пересечения геодезического и геомагнитного экваторов. В простейшем случае МПЗ в точке O представляется магнитным потенциалом диполя, когда вектор индукции магнитного поля Земли B = Bb с модулем B = µem M⊕aom /ro3(t), m где µe – магнитная проницаемость вакуума и aom – модуль вектора aom =m⊕ - 3〈m⊕,ro〉ro , bmm
= a o m / a o m .
Используется связная с корпусом КА система координат (ССК) B (O xyz ) (body) с ортами b i , направленными по соответствующим осям ССК. Ориентация ССК B в ИСК I ⊕ определяется кватернионом Λ = ( λ0 , λ ) , где λ = { λ i } , вектором параметров Эйлера Λ = { λ0, λ } , который представляется в форме Л = {C ф /2 , e e S ф /2 } с ортом e e мгновенной оси Эйлера и углом Φ собственного поворота, а также вектором модифицированных параметров Родрига (МПР) О = { о i } = е е tg( Ф / 4) , который однозначно связан с кватернионом Л прямыми О = Х / (1 + Х 0) и обратными X 0 = (1 -о 2)/(1 + о 2) , Х = 2 о /(1 + о 2 ) соотношениями.
Связанная с панелями солнечных батарей (СБ) система координат (РСК) P (Opxpypzp) определяется так: ось Opyp и орт p2 совпадают по направлению с нормалью np к плоскости фотоэлементов панелей СБ, ось Opzp и орт p3 совпадают по направлению соответственно с осью Oz и ортом b3 ССК, а ось Opxp дополняет РСК до правой ортогональной. Угловое положение панелей СБ относительно ССК определяется углом уp = У их поворота вокруг оси Oz ССК. В парковом положении панелей СБ на корпусе КА угол уp = 0, при этом направления осей РСК и ССК совпадают.
При составлении модели движения спутника начало ССК (точка O ) считается полюсом, который совпадает с ЦМ КА при недеформиро-ванном состоянии его конструкции. Кинематические соотношения для кватерниона Л и вектора МПР с имеют вид
Л = Л о ®/2;
а = |(1 - а 2 ) ® +1 a x ® + 1 ( а , ® ) а (1)
соответственно, динамика углового движения КА описывается уравнением
J ( y ) ® = -®x K + M p + M m + M g . (2)
Здесь K = J (у)® — вектор кинетического момента (КМ) КА; ® = {®i} - вектор абсолютной угловой скорости КА, представленный в ССК Oxyz ; J(y ) = Jo + 2Jp(y ) - тензор инерции КА при произвольном положении панелей СБ, при этом изменяемая часть тензора инерции каждой панели СБ в ССК представляется в виде
J p( y ) =
j p с 2 + j p s 2
JPXyd C 2 S 2
о
JpyC S о xy 2 2
jps2+jyс2 о о jp где Jp, Jy и Jp - собственные моменты инерции каждой панели в ее ЦМ и Jpyd = jp - jy ; столбец
M p = { (j py (S 2 , ro , - C 2 ,№ ) - 2J ' ^ 2 ) Y
- (jpy(C27ш, - S^ro,) + 2JP^) Y - 2JP y} представляет вектор момента инерционногироскопических сил из-за подвижности двух панелей СБ; Mm = {mm} - вектор управляющего механического момента магнитного привода (МП) и вектор гравитационного момента Mg = {mf} = (3це/r3)o2 x J(y)o2, где це -геоцентрическая гравитационная постоянная и орт o2 представлен в ССК. Вектор управляющего механического момента МП формируется по формуле Mm = {mm} =-L x B, где вектор электромагнитного момента (ЭММ) L = {li} с ограниченными компонентами | li | < lm и вектор индукции магнитного поля Земли B с ортом b определены в ССК.
Бортовая навигационная система (БНС) с применением аппаратуры спутниковой нави- гации на основе обработки сигналов спутниковых навигационных систем ГЛОНАСС/GPS формирует в моменты времени tl+1 = tl + Tp , l е N0 = [0,1,2,3...) измеренные в ГСК Ee с периодом Tp значения как векторов расположения и скорости поступательного движения ЦМ КА, так и кватерниона ориентации КА [1]. Измерения этих переменных преобразуются в их значения относительно ИСК I е по явным аналитическим соотношениям. При определении ортов r0 = ro/ ro и v0 = vo/ v0 положение ортов o1, o2 и o3 ОСК O в ИСК Ie вычисляется на борту КА по алгоритму o3 = (r0 x v0)/ | r0 x vol; o2 = ro ; 01 = o3 x o2.
Будем считать, что в моменты времени ts с периодом T q , t s + 1 = t s + T q , s е N 0 с помощью магнитометра (ММ) измеряется вектор индукции МПЗ B = B b , а в моменты времени tr с периодом T™ , t r + 1 = t r + T m , r е N 0 формируется цифровое управление МП, когда значения компонентов вектора ЭММ L = { l i } фиксируются V t Е [ t r , t r + 1 ) .
ПОСТАНОВКА ЗАДАЧИ
При возникновении команды перехода в энергосберегающий аварийный режим панели СБ приводятся в парковое положение, отключается электропитание электромеханических и реактивных приводов, выключается бесплат-форменная инерциальная навигационная система (БИНС) и некоторые другие потребители бортовой электроэнергии, а СУО переходит в режим успокоения - остановки вращения корпуса КА в ИСК I е с помощью цифрового управления магнитным приводом [2,3]. При выполнении условия ® < ®4 =0.1 град/с для модуля ® = | ® | вектора угловой скорости ® произвольного направления в некоторый момент времени t = t i начинается переход СУО в АР, где цифровое управление МП выполняется только при движении КА по части ССО, освещенной Солнцем.
В используемой концепции такого перехода с применением БНС, ММ и МП предусмотрено три этапа: 1) перевод ориентации корпуса КА к требуемой в ИСК Iе относительно орта s направления на Солнце; 2) угловая стабилизация корпуса КА, накопление измерительной информации и перевод ориентации корпуса КА в такое усредненное за виток ССО угловое положение в ИСК I е , относительно которого устанавливаются устойчивые нелинейные колебания на каждом витке орбитального движения спутника, обусловленные противодействующими влияниями гравитационного момента и управляющего момента МП; 3) продолжение угловой стабилизации корпуса КА с помощью МП и разворот панелей СБ с помощью шагового привода относительно корпуса КА к такому положению, где будет достигаться минимальное усредненное за виток ССО угловое рассогласование ϕsp = arccos 〈np , s〉 между ортом np в РСК P и ортом s направления на Солнце.
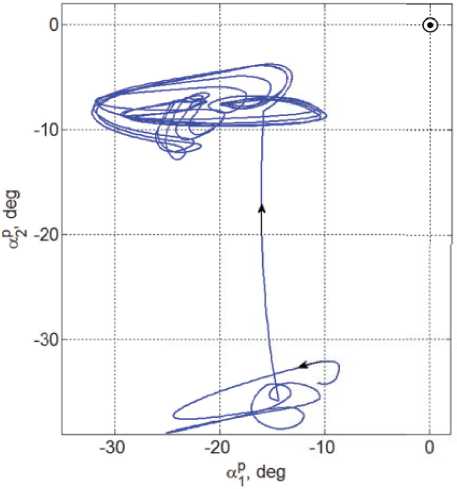
Угловое положение орта s относительно плоскости земного экватора в течение года изменяется в диапазоне [-ε e , ε e ] . Для наглядного представления детальной информации о положении орта n p относительно орта s вводится подвижная солнечно-эклиптическая система координат (ПСЭСК) O ⊕ x e s y e s z e s с началом в центре Земли O ⊕ , где ось O ⊕ x e s направлена по орту s , ось O ⊕ z e s совпадает по направлению с осью Os ZsI инерциальной солнечно-эклиптической СК I s , а ось O ⊕ y e s дополняет систему до правой ортогональной. Положение орта n p относительно орта s в ПСЭСК определяется углом α p 2 наклона орта n p к плоскости земного экватора (аналог широты) и углом α 1 p отклонения проекции орта n p на плоскость земного экватора от оси X e I ИСК I ⊕ (аналог долготы). Для любой ССО высотой до 1000 км угловое рассогласование между направлениями из центра Земли O ⊕ и из центра масс O спутника на центр Солнца O s не превышает 10 угл. сек. Такое рассогласование в дальнейшем не учитывается.
Задача статьи заключается в разработке алгоритмов цифрового управления МП на всех этапах перехода СУО спутника землеобзора в аварийный режим и последующего длительного поддержания этого режима, а также в исследовании разработанных алгоритмов с помощью компьютерной имитации.
АЛГОРИТМЫ УПРАВЛЕНИЯ
В парковом положении панелей СБ направления осей РСК и ССК совпадают, при этом орт np=p2=b2. На основе значений орта s направления на Солнце и орта no нормали к плоскости орбиты в ИСК I⊕ на борту КА определяется орбитальная солнечная система координат (ОССК) S с ортами s1,s2 и s3 , которые формируются по соотношениям s2 =s; s3 =(s×no)/|s×no | ; s1 =s2×s3 (3).
Для вычисления требуемого углового положения ССК B с ортами b i в ИСК I ⊕ формируется матрица С = С 8 = {[ s i ]} в виде столбца, составленного из строк [ s i ] ≡ s i t . Целевой кватернион Л 8 = ( X 0 ,X 8) ориентации ССК в ИСК I ⊕ определяется по матрице ориентации С 8 = {[ c ij ]} , i, j ^ 1 ^ 3 на основе явных соотношений
X 0 = (1 + tr С 8)1/2/2;
X 8 = ( c i + i i + 2 - c i + 2 i + i )/(4 X 0 ); (4)
i = 1 - 3, i + 3 = i .
Для исключения неопределенности типа (0/0) в процессе вычисления λ i s , i = 1 ÷ 3 с помощью этих соотношений при значении X 0 = 0 используется изве с тный алгоритм С. Стенли. Кватернион Е 8 = Л 8 о Л = ( e 0 , е 8 ) , вектор МПР о 68 = { о е8} = tg( Ф е / 4) е 6 , векторы ф 68 = 2 e 0 е 8 = 81п( Ф е ) е = и р 68 = { р Г} = 4 о 68 = 4tg( O 6/4) е ^ полностью определяют погрешность ориентации ССК B относительно ОССК S . Отметим, что tg( Φ e /4)=1 при Φ e = π и диапазон практически линейной зависимости вектора ρ es = 4tg( Φ e / 4) e e от угла Φ e в два раза превосходит диапазон такой же зависимости вектора р 68 = 4tg( Ф е / 4) е е . Поэтому в контуре управления КА с помощью МП используется вектор углового рассогласования £ = — р 68 .
Отфильтрованные сигналы ММ в моменты времени tr = r Tu m принимают значения B r ≡ B ( t r ) = B r b r . При формировании команды M r для вектора потребного управляющего момента на каждом полуинтервале времени t ∈ [ tr , tr + 1) с заданным периодом Tu m сначала определяется вектор потребной вариации импульса Δ I r m = Tu m M r этого момента, который представляется в виде A I “ = A I ™b + b r ( A I “ , b r ) , где вектор A I ™b = b r X ( A I “ X b r ) назначается с условием 〈∆ I r m, b r 〉 = 0 , что обеспечивает энергетическую экономичность магнитного привода. Вектор A I ™b = A I ™b i “ с модулем A I ™b и ортом i mm далее используется для формирования цифрового управления ЭММ L r = { lir } МП на периоде Tu m : определяется взаимная ориентация ортов b r и i r m в ССК, если | 〈 b r , i r m 〉 | > c s = 0.7 , то на текущем периоде дискретности МП не включается, иначе формируется вектор электромагнитного момента
L r = ( A I “ b/ T ; m)( b r X i “ )/ В r (5)
с ограниченными компонентами | l r | < 1 ™ , причем значение (5) вектора ЭММ фиксируется на полуинтервале времени t ∈ [ tr , tr + 1) . В завершении вектор управляющего механического момента МП формируется ∀ t ∈ [ tr , tr + 1) , как указано выше, в виде
М ™ ( t ) = { m “ ( t )} = — L r X B ( t ) , (6)
где вектор индукции МПЗ B ( t ) определен в ССК.
На первом этапе выполняется переориентация КА из произвольного углового по- ложения при t = ti к требуемому положению ССК в ИСК I е , которое определяется целевым кватернионом Л8. В моменты времени tr отфильтрованные сигналы БНС и ММ принимают значения Лr и Br соответственно. В эти моменты времени вычисляются кватернион Еr = (e0r, еr) = Л8 о Лr и вектор углового рассогласования еr = -рГ = -4tg(Ф® / 4) е®r. В данном режиме закон формирования потребного момента Mr принимается в виде gr+i = kb gr + kc er; Mr = J(Yr ) ku (gr + kp £r ), (7) где уr = 0, а kb, kc и kp являются постоянными коэффициентами, которые зависят от пери-m ода Tu и вычисляются по явным аналитическим соотношениям. Далее значения векторов Br = Brbr и Mr (7) используются при формировании вектора ЭММ Lr (5) магнитного привода. Здесь на каждом витке, начиная с момента времени ti, определяется среднее значение e8™ скалярной части e0s кватерниона углового рассогласования Е8 = (e8, е8). Длительность первого этапа определяется моментом времени tii, когда удовлетворяется условие e™ ^ 0.9. При рацио-m нальном назначении параметра l магнитного привода переходный процесс при любом значении угла фР (ti) = Фe(ti) < п гарантированно завершается в момент времени начала витка с номером n = 4. Здесь и далее отсчет номеров n витков ССО выполняется от момента времени очередного прохождения ее восходящего узла. В результате устанавливаются устойчивые нелинейные угловые колебания КА в окрестности «усредненного» положения орта b2 = np ССК, смещенного относительно орта s направления на Солнце в ИСК Iе . Такое смещение обусловлено витковым балансом суммарного импульса «конфликтующих» воздействий возмущающего гравитационного момента и управляющего момента магнитного привода, который «работает» только на части орбиты, освещенной Солнцем.
На втором этапе, по-прежнему при парковом положении панелей СБ ( b 2 = n Р ), начиная с момента времени t ii четвертого витка на каждом n > 4 витке ССО по сигналам БНС и отфильтрованным в моменты времени tr значениям ортов b 2( t r ) в ИСК I е накапливается сумма Е b = S b 2 ( t r ) , вычисляются ее модуль Е b = | Е b| и усредненное за виток ССО значение орта b m n = Е b / Е b . Значение орта b m n подставляется вместо орта s в соотношения (3) и (4) для формирования очередного значения
Л8т 8m 8m n+1 = (*о n+i,* n+i) для следующего витка ССО с номером n +1. Такие коррекции целевого кватерниона выполняются на четвертом, пятом и шестом витках ССО.
Третий этап, завершающий процесс перевода КА в режим аварийной ориентации, начинается в момент t = tiii начала витка с номером n = 7. Здесь выполняется разворот панелей СБ на угол у = уn относительно оси Oz ССК. Этот угол определяет положение орта p 2 = nР нормали к плоскости панелей СБ, который в ССК представляется в виде столбца p2(у) = {-SY,СY.0}. В момент времени t = tiii известно усредненное на предыдущем витке значение орта b2mn в ИСК I е , который в ССК B имеет представление bmb ее {Amb ,bm ,1^ } = Л(Л..)оЬт oMt...Y 2 n 2 n x , 2 ny , 2 nz ш 2 n ш
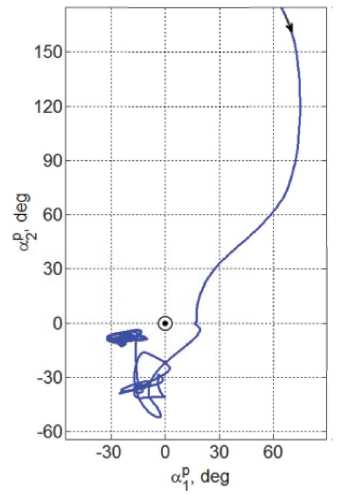
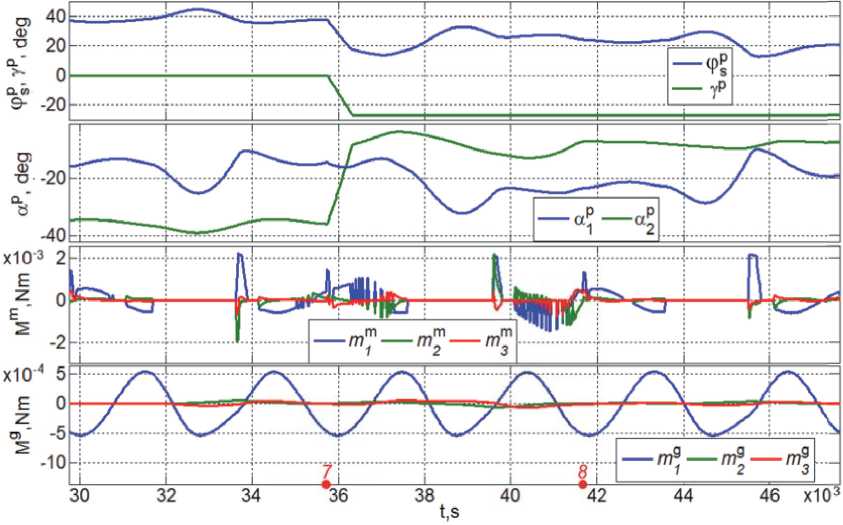
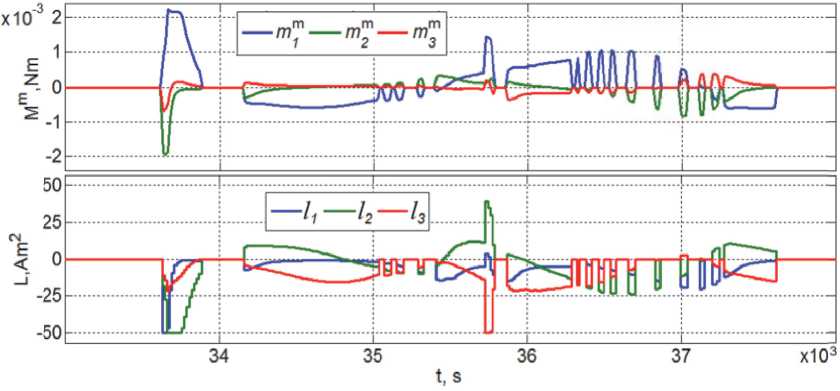
Оптимальное значение угла у = уn определяется из условия f (Y) ^ Рис. 3. Угловое рассогласование при наведении и слежении панелей СБ за Солнцем на 15 витках Vsn = arcta.J /<;. /b^). (8) Нетрудно сообразить, что в общем случае ось Oz и орт b3ССК не ортогональны плоскости, которая содержит усредненное на предыдущем витке ССО значение орта b2mn , соответствующее направлению на Солнце. Поэтому такой разворот панелей СБ может лишь свести к минимуму усредненное угловое рассогласование фр = arccos (np, s) между ортом npк плоскости панелей СБ и ортом s направления на Солнце. На последующих витках ССО с номерами n > 7 на борту КА рассчитываются очередные значения целевого кватерниона Лsmи потребного угла поворота уsпанелей СБ, но их фактический разворот рационально выполнять с периодичностью 2 раза в месяц, так как угловое положение орта s относительно плоскости земного экватора изменяется со средней угловой скоростью « 3.19 град/месяц. КОМПЬЮТЕРНАЯ ИМИТАЦИЯ АВАРИЙНОГО РЕЖИМА Имитация АР выполнена для спутника зем-леобзора массой 1000 кг на ССО высотой 720 км и наклонением 98.26 град. Расчет орбиты выполнен на дату 20.03.2017 при ее начале в восходящем узле, которому соответствуют географические координаты подспутниковой точки 30 град. ВД и 0 град. СШ, когда местное время равно 10 часам утра. При парковом положении панелей СБ (ур= 0) тензор инерции спутника J = diag{812, 587, 910} кг.м2, а моменты инерции каждой панели таковы: Jp = 16 кг.м2, jy = 8 кг.м2 и p10 кг.м2. z При имитации было принято, что БНС в моменты времени tl с периодом Tp = 1 с формирует измеренные в ГСК значения кинематических параметров орбитального движения центра масс и кватерниона ориентации спутника, которые в эти же моменты времени tl преобразуются в их значения относительно ИСК Iфпо явным аналитическим соотношениям. Также считалось, что в моменты времени ts с периодом Tq = 1 с магнитометр измеряет вектор индукции МПЗ B = B b, а после дискретной фильтрации доступных измерений в моменты времени tr. с периодом Tum= 16 с формируется цифровое управление МП (5), когда компоненты вектора ЭММ L = {li}, | li |< lm= 50 Ам2 фиксируются V t G [ tr, tr+1) . В ИСК I фначальные условия углового движения КА в момент времени t = ti, когда на первом витке ССО начинается переход СУО в аварийный режим, были назначены в следующем виде: вектор угловой скорости о(ti) = 0 и угол фp между ортом b2ССК (совпадающего с ортом npк плоскости панелей СБ при их парковом положении) и ортом s направления на Солнце принимает максимально возможное значение фp(ti) = п. На рис. 3 и 4 приведены графики изменения углового рассогласования фp, углов ap и apпри наведении и слежении панелей СБ за Солнцем на 15 витках. Нелинейные колебания спутника в аварийном режиме, которые отражаются вариациями углов ap и ap начиная с пятого витка при развороте СБ на седьмом витке, представлены на рис. 5. Рис. 4. Переход спутника в АР и его колебания на 15 витках Рис. 5. Колебания КА в АР начиная с пятого витка при развороте СБ на седьмом витке Рис. 6. Колебания КА и механические моменты в АР при развороте СБ на седьмом витке Рис. 7. Механический и электромагнитный моменты МП на шестом и седьмом витках На рис. 6 и 7 приведены некоторые результаты имитации АР в зависимости от времени при его отсчете от значения t = ti. Так, рис. 6 представляет вариации углов фР, а2 и аР, которые обусловлены угловыми колебаниями корпуса спутника относительно орта s направления на Солнце, изменение угла у2при развороте панелей СБ на седьмом витке, а также компонентов векторов управляющего момента Mm= {m™} магнитного привода и возмущающего гравитационного момента Mg= {m^}. Изменения компонентов векторов механического Mmи электромагнитного L = {li} моментов МП на части шестого и седьмого витков приведены на рис. 7, где детально представлено цифровое формирование ЭММ магнитного привода. ЗАКЛЮЧЕНИЕ Разработаны алгоритмы энергосберегающего цифрового управления магнитным приводом для ориентации информационного спутника в аварийном режиме (АР), где необходимые измерения выполняются бортовой навигационной системой по сигналам спутников ГЛОНАСС/ GPS и трёхосным магнитометром. В отличие от известных приемов выполнения АР информационных КА, в статье впервые предлагается новая схема АР и исследуются не только процессы наведения орта к плоскости панелей СБ в направлении Солнца, но и назначается требуемое угловое положение корпуса КА относительно этого направления. Реализация разработанного оригинального приема достигается с помощью виртуальной подвижной солнечно-эклиптической системы координат, которая формируется на борту КА по фактическим данным о направлении на Солнце и положении оси, ортогональной плоскости эклиптики, в процессе движения спутника по возмущенной орбите. При этом устанавливаются устойчивые нелинейные пространственные угловые колебания корпуса КА с небольшой «амплитудой» относительно направления, смещенного от орта направления на Солнце. Этот эффект обусловлен соблюдением виткового баланса суммарного импульса «конфликтующих» воздействий возмущающего гравитационного момента и управляющего момента магнитного привода, который включается только на части орбиты, освещенной Солнцем. Приведены результаты компьютерной имитации аварийной ориентации спутника землеоб- зора на солнечно-синхронной орбите высотой 720 км.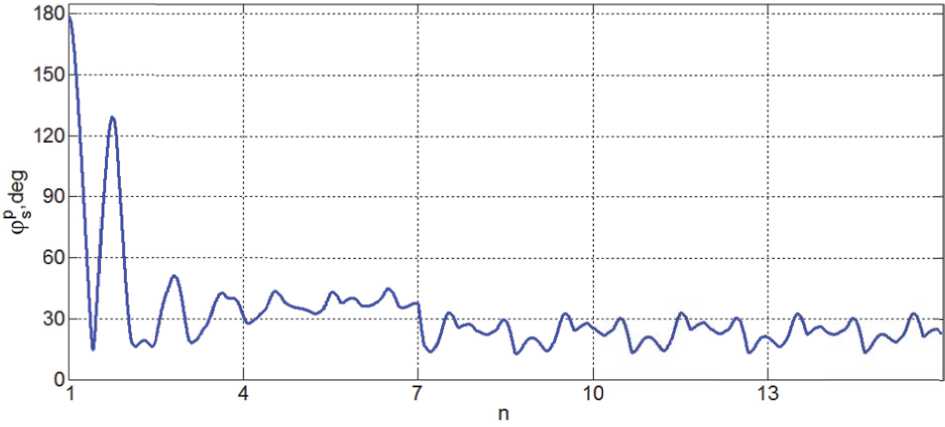
Список литературы Энергосберегающее цифровое управление магнитным приводом в аварийном режиме ориентации спутника
- Determining the attitude of the advanced crew transportation spacecraft «Federatsiya» from measurements of global navigation satellite systems/E.A. Mikrin, M.V. Mikhailov, S.N. Rozhkov, A.S. Semyonov//Proceedings of 24th Saint Petersburg International Conference on Integrated Navigation Systems. 2017. P. 94-105.
- Somova T.Ye. Guidance and digital attitude control of a maneuvering land-survey satellite//Proceedings of 24th Saint Petersburg International Conference on Integrated Navigation Systems. 2017. P. 564-568.
- Сомова Т.Е. Экономичное цифровое управление ориентацией информационного спутника в начальных режимах//Известия Самарского научного центра РАН. 2017. Том 19. № 4. С. 70-80.


