Энтропия пространственно-энергетических взаимодействий

Понятие энтропии возникло на основе второго закона термодинамики и представлений о приведенном количестве теплоты.

В статистической термодинамике энтропия изолированной и находящейся в равновесии системы равна логарифму вероятности нахождения ее в определенном макросостоянии:

S = k lnW ,              (1)

где W – число доступных состояний системы или степень вырождения микросостояний; k – постоянная Больцмана.

Или:

W = e ^S/k,

Эти соотношения являются общими утверждениями, имеющими макроскопический харак- тер, не содержат никаких ссылок на элементы структур рассматриваемых систем и полностью не зависят от микроскопических моделей [1].

Поэтому применение и рассмотрение этих законов могут иметь большое число следствий, которые наиболее плодотворно используются статистической термодинамикой.

При любых самопроизвольных изменениях в изолированной системе энтропия всегда возрастает: D S > 0.

Смысл второго закона термодинамики сводится к следующему:

Природа стремится от состояний менее вероятных к состояниям более вероятным. Так, наиболее вероятным является равномерное распределение молекул по всему объему. С макрофизической точки зрения эти процессы заключаются в выравнивании плотности, температуры, давления и химических потенциалов, а основной характеристикой процесса является термодинамическая вероятность – W .

В реальных процессах в изолированной системе рост энтропии неизбежен – в системе нарастает беспорядок, хаос, идет понижение качества внутренней энергии.

Термодинамическая вероятность равна числу микросостояний, отвечающих данному макросостоянию.

Поскольку степень вырождения системы никак не связана с физическими особенностями систем, статистическое понятие энтропии может иметь и другие применения и проявления (кроме статистической термодинамики).

«Ясно, что из двух совершенно разных по своему физическому содержанию систем энтропия может быть одинаковой, если у них число возможных микросостояний, отвечающих одному макропараметру (неважно, какой это параметр) совпадают. Именно поэтому понятие энтропии можно использовать в самых разнообразных областях. Возрастающая самоорганизация человеческого общества ... приводит к возрастанию энтропии и беспорядка в окружающей среде, что выражается в частности к появлению громадного числа рассеянных по Земле свалок» [1].

В данном исследовании делается попытка применения понятия энтропии ко ценке степени пространственно-энергетических взаимодействий.

Пространственно-энергетический параметр

Сопоставление многочисленных закономерностей физических, химических и биологических процессов позволяет предположить, что во многих случаях выполняется принцип сложения обратных величин, объемных энергий или кинетических параметров взаимодействующих структур.

Уравнение Лагранжа для относительного движения системы двух взаимодействующих материальных точек с массами m ₁ и m ₂ в координате х имеет вид:

,, д U    111

^mX = —, где — = —+ — (2),(2а), дx       m_r m 1 m 2

где U – взаимная потенциальная энергия материальных точек; m _пр – приведенная масса.

Это уравнение можно привести к виду:

A U ~ A U 1 ⁺ A U ₂ ’            ⁽³⁾

в котором результирующая энергетическая характеристика системы взаимодействия двух материальных точек находится по принципу сложения обратных величин исходных энергий взаимодействующих подсистем.

«Электрон с массой m, движущийся около протона с массой М, эквивалентен части- це с массой: mr =

mM m + M

» [3, с. 12].

Поэтому, модифицируя уравнение (3), можно предположить, что энергия валентных орбиталей атома (ответственная за межатомные взаимодействия) может быть рассчитана [4] по принципу сложения обратных величин некоторых исходных энергетических составляющих, согласно уравнениям:

—;— + = — или — +---- (4Y5)

q ²/ r, W i n, P e       P _o ( WrnV )⁽⁵⁾

^PE = P ⁰ ,                  (6)

где Wi – орбитальная энергия электронов [5]; ri– орбитальный радиус i-ной орбитали [6]; q = Z*/n* – по [7, 8], ni – число электронов данной орбитали, Z*и n* – эффективный заряд ядра и эффективное главное квантовое число, r – размерные характеристики связи.

Величина Р_О названа пространственноэнергетическим параметром (далее – ПЭП), а величина Р_Э – эффективным Р -параметром (эффективный ПЭП). Эффективный ПЭП имеет физический смысл некоторой усредненной энергии валентных электронов в атоме и является прямой характеристикой электронной плотности в атоме на данном расстоянии от ядра ( r_i ).

При образовании твердого раствора и в других структурных равновесно-обменных взаимодействиях в местах соприкосновения атомов-компонентов должна устанавливаться единая электронная плотность. Этот процесс сопровождается перераспределением электронной плотности между валентными зонами обеих частиц и переходом части электронов из одних внешних сфер в соседние.

Очевидно, что при близости электронных плотностей в свободных атомах-компонентах процессы переноса между граничными атомами частиц окажутся минимальными, что будет благоприятствовать образованию новой структуры. Таким образом, задача оценки степени таких структурных взаимодействий во многих случаях сводится к сравнительной оценке электронной плотности валентных электронов в свободных атомах (на усредненных орбиталях), участвующих в процессе по уравнениям:

a =

P o / r i - PJ r'i ( p₀/ r i +p ; / r i )/2

X 100%

или

Ре-Ре a = pTPS x 200%,         (8)

PS + PS где Рс– структурный параметр, находится по уравнению:

11  1

--- — ----- Г +-- V + ... ,

P N P' N P"

S 1 E 2 E

где N ₁ и N ₂ – число однородных атомов в подсистемах.

По всем полученным данным была построена номограмма зависимости степени структурного взаимодействия ( r ) от коэффициента a , единая для широкого класса структур (см. рисунок).

Данный подход дал возможность оценить степень и направление структурных взаимодействий процессов фазообразования, изоморфизма и растворимости в многочисленных системах, в том числе в молекулярных.

Такая номограмма может быть представлена и в виде линейной логарифмической зависимости:

a — P In ( p ^-1) ,                (10)

где коэффициент b – постоянная величина для данного класса структур. От среднего значения величина b структурно может изменяться в основном только в пределах ± 5 %.

Таким образом, коэффициент a обратно пропорционален логарифму степени структур-

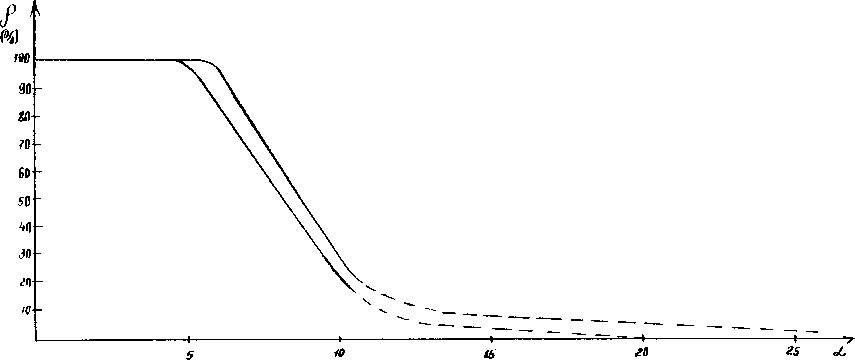
Номограмма зависимости степени структурных взаимодействий ( r ) от коэффициента a

ных взаимодействий и поэтому может характеризоваться как энтропия пространственноэнергетических взаимодействий атомно-молекулярных структур.

Действительно, чем больше r , тем более вероятно образование стабильных упорядоченных структур (например, образование твердых растворов), то есть тем меньше энтропия процесса. Но тем меньше и коэффициент a . То есть относительная разность пространственно-энергетических параметров взаимодействующих структур может быть количественной характеристикой энтропии этого процесса:

a = S = в ln ( p ^{- 1}) - (10а)

Уравнение (10) не имеет полной аналогии с уравнением (1) Больцмана, так как в данном случае сравниваются не абсолютные, а только относительные значения соответствующих характеристик взаимодействующих структур, которые могут выражаться в процентах. И это касается не только коэффициента a , но и сравнительной оценки степени структурных взаимодействий ( r ), например – процент содержания атомов данного элемента в твердом растворе, относительно общего числа атомов.

Поэтому в уравнении (10) коэффициент k = 1.

Энтропия укрупнения бизнес-структур

Основные свойства бизнес-систем, обеспечивающие их экономические преимущества, это: 1) эффективная конкуренция и 2) максимальная личная заинтересованность каждого сотрудника.

Но на различных уровнях концентрации экономики эти первопричинные особенности функционируют и проявляют себя по-разному. Наибольшая их эффективность соответствует малому бизнесу, когда число членов организации минимально, более четкая личная заинтересованность и активная конкурентная борьба за выживание. По мере укрупнения предприятий и производств, с увеличением численности персонала роль каждого сотрудника постепенно снижается, уменьшается конкурентная борьба, так как появляются новые возможности для согласованных дей- ствий разных бизнес-структур. Идет снижение качества экономических отношений в бизнесе, то есть возрастание энтропии. Более всего такой процесс характерен в моноструктурах на крупнейших предприятиях большого бизнеса (синдикаты и картели).

Понятие термодинамической вероятности как числа микросостояний, отвечающих данному макросостоянию, можно модифицировать применительно к процессам экономических взаимоотношений, которые напрямую зависят от параметров бизнес-структур [9].

За макросостояние системы можно принять данную отдельную бизнес-структуру, а за число микросостояний – число ее сотрудников ( N ), которое есть число доступных наиболее вероятных состояний данной бизнес-структуры. Таким образом, предполагается, что такое число сотрудников бизнес-структу-ры является аналогом термодинамической вероятности применительно к процессам экономических взаимоотношений в бизнесе.

Поэтому можно принять, что общая энтропия качества бизнеса состоит из двух энтропий, характеризующих: 1) уменьшение эффективности конкуренции ( S ₁) и 2) уменьшение личной заинтересованности каждого сотрудника ( S ₂), то есть: S = S ₁ + S ₂. Величина S ₁ пропорциональна числу работников предприятия: S ~ N , а величина S ₂ имеет сложную зависимость не только от числа работников предприятия, но и от эффективности самого управления им. Она обратно пропорциональна персональной заинтересованности каждого сотрудника. Поэтому можно принять, что S ₂= 1/ g , где g – коэффициент личной заинтересованности каждого сотрудника.

По аналогии с уравнением Больцмана (1) получаем:

ГО   (nA

S = ( S 1 + S 2 )~[ In— + In l — I ]~ln l — I к Y )     I Y )

или

( — )

S = kln l — I , к Y )

где k – коэффициент пропорциональности.

Здесь N показывает во сколько раз данная бизнес-структура больше эталонной структуры малого бизнеса, при которой N = 1, то есть эта величина не имеет наименования.

Для нетермодинамических систем принимаем k = 1. Поэтому:

I N S = In I —

I Y.

В таблице приведены примерные расчеты бизнес-энтропии по уравнению (11) для трех основных уровней бизнеса: малого, среднего и крупного. При этом предполагалось, что число N соответствует некоторому среднему значению из наиболее вероятных величин. Подробнее в работе [10].

При расчете коэффициента личной заинтересованности g учитывалось, что он может меняться от 1 (один сотрудник работает только сам на себя) до ноля (0), если такой работник как бесправный раб, и для наиболее крупных предприятий принималось g = 0,1 – 0,01.

Несмотря на весьма приближенную точность таких усредненных расчетов, можно сделать достаточно достоверный вывод о том, что энтропия бизнеса с укрупнением его структур резко возрастает при переходе именно от среднего к крупному бизнесу, так как снижается качество бизнес-процессов. Применение более точных исходных данных позволит получить конкретные значения энтропии бизнеса, выше которых процесс экономических отношений может выйти на критический уровень.

Сравнение номограммы (см. рисунок) с данными таблицы показывает аддитивность величин энтропии бизнеса ( S ) со значениями коэффициента пространственно-энергетических взаимодействий ( a ).

Более того, значения коэффициента a для высокой степени структурных взаимодей- ствий (до 7 %) совпадают со значениями энтропии для малого и среднего бизнеса. Такая закономерность изменения величин сохраняется и далее: для ограниченной степени структурных взаимодействий по номограмме идет резкое возрастание коэффициента a и аналогично резко возрастает величина S при переходе от среднего к крупному бизнесу.

Все это подтверждает утверждение о том, что понятие энтропии имеет множественное проявление в самых разнообразных областях исследований.

Вывод

Аналогично представлениям термодинамики о статистической энтропии можно использовать понятие энтропии пространственно-энергетических взаимодействий.