ЭПР-дозиметрия по эмали зубов: выделение радиационно-индуцированного сигнала в спектре ЭПР эмали с использованием модели, учитывающей зависимость формы компонентов спектра от микроволновой мощности

Ретроспективное определение величины радиационного воздействия на население и персонал имеет большое значение для анализа радиационного риска и является важной частью многих радиационно-эпидемиологических исследований. В частности, методы индивидуальной ретроспективной дозиметрии необходимы, когда такие исследования проводятся в случаях, если обычные методы инструментальной дозиметрии недоступны.

Для ретроспективной оценки индивидуальных накопленных доз облучения в случаях неконтролируемого воздействия радиации может быть использована ЭПР-спектроскопия образцов эмали зубов человека, удалённых по медицинским показаниям. Этот метод, называемый ЭПР-дозиметрия по эмали зубов, на протяжении ряда лет успешно применяется для определения доз радиоактивного облучения в аварийных и неконтролируемых ситуациях [1].

Известно, что спектр ЭПР облучённых образцов эмали зубов состоит из двух основных сигналов – нативного фонового сигнала (ФС) и радиационно-индуцированного сигнала (РС) [1, 6]. Поглощённая доза в эмали может быть определена на основе измерения интенсивности РС с использованием калибровочной зависимости. В области относительно малых доз (0-500 мГр), представляющей интерес в радиационной эпидемиологии, РС существенно маскируется ФС, что затрудняет измерение его интенсивности. Для того чтобы выделить РС, необходимо проводить специальную математическую обработку спектра ЭПР. Выбор оптимального

Санин Д . Б .* – н.с.; Иванников А . И . – в.н.с., Скворцов В . Г . – зав. лабораторией. МРНЦ РАМН.

способа обработки спектра является очень важным для достижения надежного результата при определении поглощённой дозы.

По результатам межлабораторных интерсличений подходов к реализации метода ЭПР-дозиметрии [15, 16] можно отметить несколько наиболее эффективных способов обработки спектров ЭПР в области малых доз, применение которых позволяет получить наибольшую точность измерения интенсивности РС. Один из способов основан на ручной подгонке предварительно измеренного образцового ФС к экспериментальному спектру с вариацией его амплитуды, ширины и положения по магнитному полю [12]. Недостатком такого способа является то, что надежность получаемых результатов зависит от квалификации и опытности оператора. Поэтому для осуществления возможности массового использования метода ЭПР-дозиметрии необходима разработка и использование способов автоматической обработки спектров с минимальным вмешательством оператора. Наиболее перспективными представляются способы, основанные на подгонке модельного спектра к экспериментальному спектру методом наименьших квадратов (МНК).

Можно отметить два основных подхода к формированию модельного спектра. В одном из подходов модельный спектр составляли из предварительно измеренных образцовых ФС и РС, представленных в цифровом виде (цифровая модель) [11, 14]. В другом подходе модельный спектр составляли из ФС и РС, описанных аналитической функцией (аналитическая модель) [4, 8].

В обоих подходах для более точного описания формы ФС и учета ее вариации для индивидуальных образцов, ФС составляли из комбинации основного квазиаксиального компонента и дополнительного, симметричного компонента. При этом, в качестве дополнительного компонента использовали широкий компонент с положением центра близким к основному компоненту [8], либо узкий дополнительный компонент, смещенный в область высокого поля [10, 11]. Для учета индивидуальной вариации формы ФС, амплитуду дополнительного компонента варьировали при подгонке МНК, а ширину основного компонента оставляли фиксированной [10, 11], либо также варьировали [8]. Природу дополнительного компонента либо не идентифицировали [10], либо узкий выскопольный компонент относили к сигналу, индуцированному механическим и температурным воздействием при подготовке образцов эмали [3].

В работе [14] сравнивали подходы к математической обработке с применением аналитической и цифровой моделей для одного и того же набора спектров, измеренных для образцов эмали зубов, облученных в разных дозах. Более высокая точность была получена при использовании аналитической модели.

На основе данных, полученных в процессе межлабораторного интерсличения, производили сравнение разных способов обработки спектров облученной эмали зубов [7]. Одни и те же наборы спектров, измеренные в различных лабораториях для одних и тех же образцов, были обработаны в трех лабораториях обычно используемыми ими способами с применением аналитической или цифровой модели. Результаты сравнения этих способов указывают на то, что точность определения амплитуды РС зависит от того, насколько данный способ адаптирован к параметрам регистрации спектров, влияющим на форму линий его компонентов. Для достиже- ния высокой точности результата обработки форма компонентов в аналитической модели может быть легко измена путем выбора соответствующих величин параметров описывающей ее функции. В случае цифровой модели необходимо, чтобы базовые спектры, из которых составлена модель, были измерены при условиях регистрации, максимально близких к условиям регистрации анализируемого спектра. Эти модели имеют свои преимущества и недостатки и, по-видимому, следует разрабатывать оба этих подхода. В данной работе проводятся исследования, направленные на повышение точности обработки спектров с использованием аналитической модели в случае, когда спектры были измерены при различных параметрах регистрации.

Одним из основных параметров регистрации, влияющих на форму компонентов спектра, является микроволновая мощность, подводимая к резонатору спектрометра. Ранее проводили испытание аналитической модели при различной мощности для двух различных типов спектрометров [9, 17]. Использовали модель с ФС, который описывали суммой основного узкого квази-аксиального и широкого симметричного компонентов. Изменение формы ФС при различной мощности учитывалась путем вариации ширины основного компонента и соотношения амплитуд основного и дополнительного компонентов при подгонке МНК, а форма РС устанавливалась при этом фиксированной. Было показано, что применение данной модели дает максимальную точность при некотором значении мощности, которое зависит от типа используемого резонатора, и предложено в качестве оптимального для измерения спектров. Недостатком примененной модели является то, что не учитывали изменение формы РС при различной мощности. Кроме того, в этой модели ФС описывали эвристической функцией с двумя компонентами, природа которых и вариация их параметров при различной мощности не обоснована физически. В процессе подгонки формы ФС МНК варьируется большое количество параметров, что приводит к пониженной устойчивости процесса и увеличивает вероятность получения ложного результата.

Недавно была предложена аналитическая модель [13], учитывающая изменение формы ФС и РС при различной мощности с обоснованием физической природы этого явления, а также более точно описывающая форму этих сигналов. С целью поиска оптимального алгоритма обработки спектров в настоящей работе производится испытание этой модели для обработки набора спектров, измеренных при различной мощности. Результаты оценки точности, характеризующей применение данной модели при разных режимах обработки спектров, сравниваются с результатами для ранее использованной модели [17], полученными для того же набора спектров.

Материалы и методы

ЭПР спектры образцов эмали

Спектры облучённых различными дозами образцов эмали были использованы те же, что и в предыдущей работе [17]. Образцы были приготовлены из смеси эмали, полученной из нескольких зубов. Эмаль была отделена от дентина с помощью твердосплавного бора и была измельчена на частицы размерами 0,5-1,5 мм.

Десять образцов эмали с массой каждого образца 100±1 мг были подвергнуты гамма-облучению источника 60Co дозой 0, 100, 200, 300 и 500 мГр по паре каждой дозой. Погрешность установки дозы не превышала 3 %.

Спектры были записаны на спектрометре JES-FA100 EPR (JEOL, Япония) в Х-диапазоне при следующих параметрах регистрации: амплитуда модуляции – 0,3 мТл, частота модуляции – 100 кГц, постоянная времени приемника – 30 мс, время развёртки – 30 с, ширина развёртки – 10 мТл. Запись спектров была произведена при микроволновой мощности 1, 2, 5 и 10 мВт, количество накапливаемых спектров 10, 20, 40, 80 и 120 для каждого значения мощности (время накопления составляло соответственно 5, 10, 20, 40, 60 мин). Измерения повторяли 4 раза при каждом наборе значений параметров после встряхивания образцов и поворота ампулы с образцом на произвольный угол для ослабления эффектов анизотропии. В результате были записано 40 спектров для каждой пары значений времени накопления и величины мощности, всего было получено 800 спектров.

Процедура математической обработки спектров

Математическую обработку спектров производили с использованием модифицированной программы на языке Visual Basik 4.0 (MicroCal Corporation), прототип которой описан в предыдущей публикации [8]. С помощью этой программы производили подгонку параметров аналитической модели к спектру ЭПР эмали МНК. При этом определяли амплитуду РС для серии спектров набора образцов, облученных в различных дозах и измеренных при одинаковых параметрах регистрации. Окно подгонки использовали то же, что и в предыдущей публикации [17], –10 мТл и +20 мТл от максимума ФС. Затем, по зависимости амплитуды РС от номинальной дозы определяли методом линейной регрессии параметры калибровочной зависимости и, используя эти параметры, определяли дозу в эмали исходя из амплитуды РС. Все вычисления в пределах каждой серии спектров выполнялись программой автоматически, оператор выбирал только серию спектров для обработки.

В качестве параметра, характеризующего точность определения дозы, для каждой серии спектров, измеренных при одинаковых параметрах регистрации, вычисляли среднеквадратичное отклонение дозы между определенными и номинальными значениями ( SDD ).

В качестве параметра, характеризующего точность подгонки модели к экспериментальному спектру, вычисляли остаточную сумму, равную среднеквадратичной амплитуде разности между подогнанным модельным и экспериментальным спектром в окне подгонки. Этот параметр пересчитывали в единицы дозы путем деления на наклон калибровочной зависимости и получали значения нормированной остаточной суммы ( RSD ).

Модель описания спектров

При математической обработке спектров использовали аналитическую модель описания спектра облученной эмали, учитывающую изменение формы линий спектра при различной микроволновой мощности, подводимой к резонатору спектрометра [13]. В соответствии с этой моделью, РС описывается следующей функцией:

Y RS (x) = A 0 {A 11 [G(x – dh 11 , D 1 ) + A 12 G(x – dh 11 – dh 12 , D 1 )

+ A 13 G(x – dh 11 – dh 13 , D 1 )] + A 2 G(x – dh 2 , D 2 ) + A 3 L(x – dh 3 , D 3 )} ,        (1)

где x = h - h 0 , h – величина магнитного поля, измеренная в мТл; h 0 – величина магнитного поля резонанса, соответствующая величине фактора Ланде g =2 (при используемой частоте микроволн 9400 МГц эта величина равна 335,83 мТл). G и L – производные функций Гаусса и Лоренца соответственно:

G(x, d) = - x/d exp [-2(x/d)²] / [0,5 exp(-0,5)] ,                                     (2)

L(x, d) = 3,08 (x/0,866 d) {1 + [x/(0,866 d)]²}² ,                                     (3)

где х – аргумент относительно центра функции; d – параметр ширины, соответствующий расстоянию между максимумами функций. Амплитуда экстремумов этих функций нормирована на единицу.

Остальные параметры в формуле (1) описывают амплитуду, форму и относительное положение компонент, составляющих РС. Значения этих параметров при использованных значениях микроволновой мощности 2, и 10 мВт взяты из работы [13], а значения при 1 и 5 мВт получены методом линейной экстраполяции и представлены в таблице 1.

Таблица 1

Параметры функции , описывающей РС при различной микроволновой мощности , использованные в модели при обработке спектров

Мощность       1	1 мВт        1	2 мВт        1	5 мВт        1	10 мВт
Основной квазиаксиальный компонент
dh 11 ( мТл )	0,091	0,091	0,092	0,093
D 1 ( мТл )	0,405	0,405	0,405	0,405
A 12	0,495	0,497	0,502	0,510
dh 12 ( мТл )	0,316	0,316	0,316	0,316
A 13	0,418	0,416	0,410	0,399
dh 13 ( мТл )	0,635	0,635	0,635	0,635
Узкий изотропный компонент
A 2	0,044	0,044	0,043	0,042
dh 2 ( мТл )	-0,432	-0,432	-0,432	-0,432
D 2 ( мТл )	0,283	0,283	0,283	0,283
Широкий изотропный компонент
A 3	0,031	0,031	0,031	0,032
dh 3 ( мТл )	0,008	0,020	0,057	0,118
D 3 ( мТл )	1,190	1,182	1,157	1,115

Форма ФС описывается следующей функцией:

Y NS (x) = A 0N [L(x – dh 1N , D N ) + 0,5 L(x – dh 1N – dh 2N , D N )] , (4)

где х – имеет то же значение, что и в формуле (1); L – производная функции Лоренца определённая в уравнении (3); dh 1N – параметр, характеризующий положение ФС относительно поля, соответствующего g =2; D N – параметр, характеризующий ширину фонового сигнала; dh 2N – параметр асимметрии сигнала; A 0N – параметр амплитуды.

Изменение формы фонового сигнала при различной микроволновой мощности учитывали с использованием параметров ширины DN и асимметрии dh2N, полученных из графиков, которые представлены в работе [13]. Значения этих параметров даны в таблице 2. Параметр dh1N в вышеуказанной работе не представлен, и его получали при подгонке МНК положения ФС относительного РС, и устанавливали равным 0,85 мТл. Параметр амплитуды A0N определяли при подгонке МНК.

Таблица 2 Параметры фонового сигнала при различной микроволновой мощности , использованные в модели при обработке спектров

Мощность	1 мВт	2 мВт	5 мВт	10 мВт
D N	0,51	0,53	0,59	0,68
dh 2N	0,33	0,31	0,28	0,24

Способы математической обработки спектров

Обработка спектров проводилась с использованием аналитической модели, описанной выше. Вариацию формы ФС учитывали с применением трех следующих способов:

Способ 1. ФС с фиксированной формой с параметрами ширины и асимметрии , устанавливаемыми в зависимости от мощности . Параметры функции, описывающие ФС при данной мощности (параметр ширины и параметр асимметрии), были получены, как указано выше, на основе данных, приведенных в работе [13].

Способ 2. ФС с переменным параметром ширины . Ширину ФС варьировали в процессе подгонки модели к экспериментальному спектру при обработке методом наименьших квадратов. При этом для каждого образца получали индивидуальное значение параметра ширины. Параметр асимметрии устанавливали фиксированным, таким же, как в Способе 1 . Хотя форма ФС зависит от двух параметров – параметра ширины и параметра асимметрии, из предварительных экспериментов, похоже, что зависимость параметра ширины от мощности сильнее влияет на результат подгонки, а также ввиду сложностей, связанных с вычислениями, на данном этапе исследований выбрали именно этот параметр в качестве переменного.

Способ 3 . ФС с фиксированным уточненным параметром ширины . В процессе обработки методом наименьших квадратов параметр ширины ФС устанавливали фиксированным, равным среднему значению для набора образцов, полученному при данной мощности с использованием модели ФС с переменным параметром ширины.

Сравнение производили с результатами, представленными в предыдущей публикации [17], полученными при обработке тех же спектров с использованием Способа 4 :

Способ 4. ФС с переменной формой . ФС описывали суммой узкой и широкой компонент с подгонкой ширины узкой компоненты и соотношения между ними. Форму РС при этом устанавливали фиксированной в соответствии с мощностью 2 мВт.

Результаты

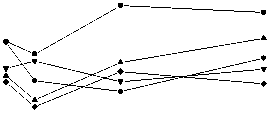
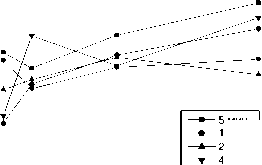
Группы спектров для набора образцов, измеренные при различных параметрах регистрации, были математически обработаны подгонкой МНК параметров моделей в соответствии со Способами 1-3. На основе полученных результатов для каждой группы спектров были опреде- лены параметры SDD и RSD. Зависимости полученных таким образом параметров SDD и RSD от мощности при различном времени накопления на примере результатов, полученных с применением Способа 1 и Способа 2, представлены на рисунках 1 и 2, соответственно. Для результатов, полученных с применением Способа 3, были вычислены зависимости, близкие в пределах нескольких процентов к результатам, полученным Способом 1.

Способ 1

—■— 5 мин

—•— 10 мин

▲ 20 мин

▼ 40 мин

—60 мин

2           4           6           8           10

Микроволновая мощность ( мВт )

Способ 2

5 мин

10 мин

20 мин

40 мин

—60 мин

2           4           6           8           10

Микроволновая мощность (мВт)

а

б

Рис . 1. Зависимости SDD от микроволновой мощности, для спектров, измеренных при различном времени накопления при обработке с использованием Способа 1 (а) и Способа 2 (б).

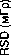
Способ 1

—■— 5 мин

—•— 10 мин

▲ 20 мин

▼ 40 мин

60 мин

2           4           6           8           10

Микроволновая мощность ( мВт )

Способ 2

—■— 5 мин

—•— 10 мин

▲ 20 мин

▼ 40 мин

60 мин

10 “I--------------1--------------1--------------1--------------1--------------1--------------1--------------1--------------1--------------1-------------10           2           4           6           8           10

Микроволновая мощность ( мВт )

а

б

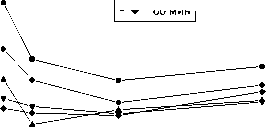
Рис . 2. Зависимость RSD от микроволновой мощности для спектров, измеренных при различном времени накопления при обработке с использованием Способа 1 (а) и Способа 2 (б).

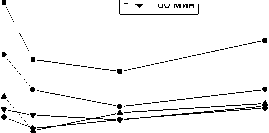
Величины SDD и RSD , полученные с использованием различных способов при различном времени накопления, были усреднены. Усреднение результатов по времени накопления было проведено для удобства сравнения зависимостей, полученных различными способами. Зависимости усредненных SDD и RSD от мощности представлены на рисунках 3 и 4. На тех же рисунках, для сравнения, показаны соответствующие зависимости для Способа 4 , взятые из работы [17].

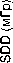
—■— Способ 1

—•— Способ 2

▲ Способ 3

▼ Способ 4

30 П-------------1-------------1-------------1-------------1-------------'------------1-------------1-------------1-------------1-------------1“

0            2            4            6            8           10

Микроволновая мощность (мВт)

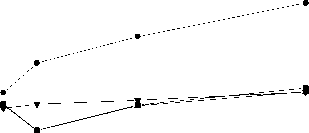
Рис . 3. Зависимость усреднённых значений SDD от микроволновой мощности.

0           2           4           6           8          10

Микроволновая мощность (мВт)

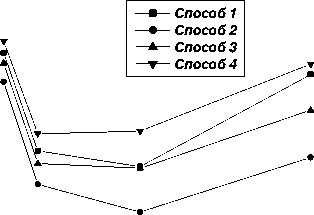
Рис . 4. Зависимость усреднённого значения RSD от микроволновой мощности.

Обсуждение

В качестве основного показателя при выборе оптимального способа обработки спектров был принят усредненный параметр SDD , поскольку он характеризует точность определения дозы. Из зависимостей усредненного SDD от микроволновой мощности, представленных на рисунке 3, видно, что данный параметр для Способов 1 и 3 имеет существенно меньшее значение, чем для Способа 2 во всем диапазоне мощности. Для Способа 4 SDD также существенно меньше, чем для Способа 2 во всем диапазоне мощности. Этот параметр для Способа 4 существенно меньше по сравнению с результатами, полученными для Способов 1 и 3 в области 2-5 мВт и близок при 1 и 10 мВт. Таким образом, использование Способов 1 и 3 с применением модели, учитывающей зависимость формы компонент от мощности, является наиболее эффективным среди испытанных здесь способов. Особо эти преимущества проявляются при мощности 2-5 мВт, которая может быть признана оптимальной для проведения измерений.

Кроме того, применение этой модели дает возможность снизить количество подгоняемых параметров, по сравнению с ранее использованным Способом 4 [17], что приводит к снижению ошибки подгонки МНК.

Из анализа зависимостей усредненного RSD от мощности (рис. 4) следует, что этот параметр не связан напрямую с параметром SDD , характеризующим точность определения дозы. Например, Способ 2 дает меньшее значение RSD по сравнению с остальными способами, хотя его SDD больше, чем у других способов. Таким образом, параметр RSD лишь характеризует, насколько близко модель описывает спектр.

Заключение

Было проведено исследование модели, учитывающей изменение формы радиационно-индуцированного сигнала в спектре ЭПР облученной эмали при различной микроволновой мощности, с использованием различных способов учёта вариации формы ФС. Показано, что использование данной модели позволяет увеличить точность определения дозы по сравнению с ранее использованной моделью, в которой форму радиационно-индуцированного сигнала устанавливали фиксированной вне зависимости от мощности, а форму нативного фонового сигнала варьировали в процессе подгонки модели к экспериментальному спектру. Для дальнейшего усовершенствования модели необходимо провести испытания на дополнительных сериях спектров, измеренных в других условиях, в частности, полученных в различных лабораториях при проведении международных интерсличений [5, 7].