Этапы информационного обеспечения разработок бортовой аппаратуры космических аппаратов

Наземная экспериментальная отработка

(НЭО) элементов, устройств и систем космиче- ских аппаратов (КА) - неизменный этап создания КА. На первых этапах становления космической отрасли технология НЭО была на уровне информационно не обеспеченного инженернотехнического «творчества» и «самодеятельности». И только время и наработанный опыт, как результат ошибок и успехов, привели к пониманию НЭО как наземного «полета», охватывающего весь комплекс особенностей полета реального с учетом ограничений, которые возникали в связи с невозможностью воспроизведения комплекса факторов космического пространства (ФКП) в их естественном проявлении. На первых этапах для этого не было достаточного фактического материала, воссоздающего действительную модель космоса. Не было необходимого оборудования для воспроизведения комплекса ФКП и, когда оно появилось, оказалось, что по ряду воздействий оно монофак-торное. В то время, как в реальной обстановке (в условиях ФКП), оно полифакторное.

Также недостаточно была разработана технология НЭО. И только запросы ядерной энергетики и космической техники придали развитию этого направления положительной импульс. Появились редакции зарубежных и отечественных публикаций, которые в конечном итоге обосновали процесс выпуском отраслевых и государственных и нормативных документов, определяющих необходимый уровень экспериментальных и исследовательских работ на этапе НЭО и необходимый объем результатов для принятия решения о возможности выхода КА за пределы конструкторского бюро и заводов-изготовителей к орбитальной работе.

Предприятия шли к этому своим путем. Статья представляет некоторые фрагменты этого процесса по пути к совершенствованию НЭО элементов бортовой аппаратуры (БА) КА.

1.    Общие положения

Весомость экспериментальной отработки сложных технических устройств, к которым относится БА КА, не теряет своей актуальности. Время вносит коррективы в технологию реализации: движение от простого макетирования будущих устройств к более совершенным факторам организации и использование моделирования на ЭВМ.

Совершенствование и оптимизация экспериментального исследования всегда сопутствовали разработке, о чем свидетельствуют публикации, пик которых был связан с успехами приборостроения различного назначения [1; 2].

Положение, что только исчерпывающая параметрическая оценка создаваемых технических устройств может обеспечивать необходимое качество создаваемого продукта и, в конечном итоге, является условием перехода от экстенсивной затратной экономики к экономике интенсивной, способствующей техническому прогрессу, – не вызывает сомнений [3]. А ряд принципов, аккумулированных в справочном пособии [1], и в настоящее время могут быть источником идей при формировании современных подходов.

Так как экспериментальная отработка БА КА реализуется в процессе испытаний в режимах и условиях, максимально приближенных к эксплу- атационным, то для исследователя важны научно обоснованные принципы организации исследований, а также оценка результатов минимально достаточного количества образцов, позволяющих принимать решения о соответствии разработки поставленным требованиям. И тогда разработка считается информационно обеспеченной.

2.    Этапы информационного обеспечения разработок бортовой аппаратуры

В общем виде эффективность испытаний может быть оценена как вероятность того, что вектор Y ^ˆ показателей качества испытаний находится ²

в области { ^ ₂^} допустимых значений [1; 2]. Таким образом, для оценки показателя эффективности необходимо иметь вектор Y , его характеристики (закон распределения или моменты) и область допустимых значений вектора. Не вдаваясь в детали формирования вектора, следует отметить, что методология оценки не может быть ориентиром для изготовителя будущего устройства, так как оценка формируется по результатам исследований, а каковы необходимы ресурсы подготовки и реализации исследований, ответа нет.

Рекомендации, исходя из ряда статистических предпосылок, содержит работа [4]. В предположении нормального распределения контролируемых параметров для практических применений могут быть достаточными результаты испытаний 30–100 образцов.

Однако с позиции современного понимания экспертного исследования последнее утверждение требует значительного уточнения и детализации.

• 2.1.    Исследование устройств

по методологии математического планирования эксперимента

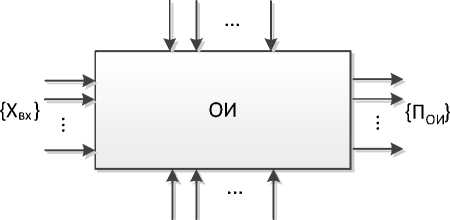
Так, если рассматривать устройство как объект исследования (ОИ) по плану активного эксперимента – МПЭ (математического планирования эксперимента) [5–7], то обобщенная графическая модель устройства в пространстве воздействий может быть представлена следующим образом (рис. 1).

Воздействиями на рассматриваемый ОИ являются:

• •    { X _вх} — входные сигналы, уровни питающих токов и напряжений;

• •    { X внш } — воздействия эксплуатационной среды (для КА – космического пространства): температура, давление, радиационные воздействия и др.;

• •    { X в _нт} — разброс параметров комплектующих, взаимодействие элементов в пространстве конструкции и др.

  
  

{Х внш }

{Хвнт}

Рис. 1. Объект исследований:

{ X _вх} - совокупность входных воздействий;

{ X _внш} — совокупность внешних воздействий;

{ X внт } — совокупность внутренних воздействий;

{Пои} – совокупность контролируемых параметров ОИ

Общее для всех воздействий (факторов) – различная физическая природа, случайные уровни в известных (предполагаемых) пределах, независимость (в большинстве случаев), возможность управления (в большинстве случаев).

Используя факторы {X _вх} и {X _внш}, учитывая их независимость и управляемость, представляют полный набор опытов для исследования зависимости П ои от изменяющихся воздействий (полный факторный эксперимент – ПФЭ) в виде таблицы - матрицы планирования (МП), партитуры представляющих исследований (табл. 1).

Таблица 1

Матрица планирования, n = 3

№ опыта	x 1	x 2	x 3	П ои
1	+	+	+	П
2		+	+	П
3	+		+	П 3
4			+	П 4
5	+	+		П 5
6		+		П 6
7	+			П 7
8				П 8

Исходная предпосылка в начале исследования – зависимость П ои от всех факторов линейная. Для ее восстановления (математической модели – ММ) вида

^Пои = ^П ( х ) = в о + ^в1 х 1 + ^В2 х 2 + - (1) достаточно каждый фактор устанавливать (варьировать) в процессе эксперимента на двух уровнях (min - «-»; max - «+»). Тогда для оценки коэффициентов влияния (в i ) факторов потребуется в общем случае N = 2 n опытов ( n - количество факторов), исчерпывающих все возможные сочетания уровней факторов (опыт – строка МП).

Том 5

Таким образом, МП - исходная база программы исследований, определяющая:

• •    номенклатуру технологического оборудования, обеспечивающего имитацию физических воздействий (стенды, установки, измерительные средства) и реального эксперимента;

• •    набор измерительно-вычислительных средств для фиксации и обработки результатов;

• •    необходимое нестандартное оборудование (подставки, кабели, переходные устройства и др.).

• 2.2.    Анализ влияния внутренних факторов

Если при этом учесть дублирующие (параллельные) опыты, необходимые для корректных статистических оценок, то МП также – исходная база для оценки финансовых и временных трат для реализации исследования по плану МПЭ. Такой хорошо структурированный исходный базис МПЭ – привлекательная сторона метода.

Следует также упомянуть этапность уточнения, виды получаемой ММ: исходная предпосылка о линейности – учет слабых нелинейных эффектов (факторов взаимодействия) при необходимости - учет явных нелинейностей при необходимости. И так до получения адекватной ММ ОИ.

Все это относится к отражению в ММ влияния тех факторов, которые подлежат варьированию при реализации ПФЭ.

ОИ на результаты ПФЭ

Остается не раскрытым влияние на результаты ПФЭ внутренних факторов, присущих большинству ОИ, когда предполагается изготовление некоторого количества однотипных образцов ОИ [8]. К таким объектам следует отнести материалы, растворы, смеси, газообразные вещества, а также электронные устройства различного назначения, являющиеся композицией большого числа составных частей.

Применительно к аппаратуре, где основной «строительный» материал – полупроводниковые структуры, каждый p - n -переход привносит в отклики итогового ОИ свой индивидуальный вклад, для которых невозможно произвести ни количественную оценку, ни оценку пределов изменчивости, а также определить характер вкладов (линейные, нелинейные), проявляется только интегральный эффект влияния { X _внт}.

Если бы подлежало оценке количество факторов в { X _внт}, то, исходя из алгоритмов МПЭ, можно было бы рассчитать примерное количество опытов, необходимое для полного выявления вкладов { X _внт}, которые «устанавливает» случай. Но такой подход проблематичен.

Можно связать вклады { X _внт} с «работой» обобщенного фактора X _внт, принимающего в каждом опыте случайные уровни в пределах ±1. Тогда наличие экстремальных «неуправляемых»

вкладов в результатах ПФЭ нескольких образцов устройства можно связать с вкладами X _внт, представленными уровнями +1 и -1. Но нет гарантии, что новые опыты не покажут результаты, превышающие полученные ранее, тем более, что вероятности появления X _внт на уровнях ±1 очень малы.

{Хвнш}

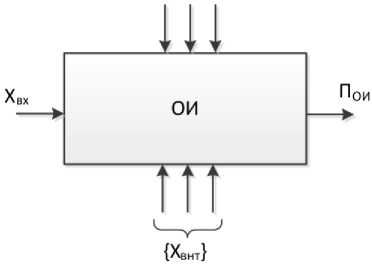
Рис. 2. Объект исследований – устройство задержки сигнала

Факторы, влияющие на время задержки (τз):

• •    величина емкости времязадающего конденсатора ( x ₁);

• •    уровни питающего напряжения ( x ₂);

• •    температура окружающей среды ( x ₃).

Если бы не было влияния внутренних факторов, то результаты ПФЭ с рядом УЗС (однотипные устройства) повторились бы с точностью ошибок измерения τ_з. Но присутствие { X _внт} вносит существенные различия в результаты.

Это подтверждают результаты исследований 24-х образцов УЗС (фрагмент результатов в табл. 2).

Чтобы продолжать рассмотрение особенностей проявления влияния { X _внт}, рассмотрим результаты ПФЭ с простым электронным устройством задержки сигнала (УЗС), реализованном на гибридной интегральной схеме, обеспечивающей задержку входного перепада напряжения в среднем на 12 с (рис. 2).

Математическая модель, восстановленная по средним значениям опытов для 24-х образцов:

Тср = Пои = 11,9925 +1,23x1-0,25 x 2 +

+ 0,195x- 0,015xx + 0,055xx +      (2)

+ 0,018x2x3 + 0,028xx2x3.

Зависимость практически линейная, влияние взаимодействий незначительное. А влияние внутренних факторов разбрасывает значения τз от 9,51 до 15,31 с.

Это может быть прослежено по изменению коэффициентов влияния в _i (табл. 3).

Таблица 2

Фрагмент результатов исследований времени задержки 24-х образцов УЗС

№ опыта	x 1	x 2	x 3	τ з, с
				τ 1	τ 2	τ 3	…	τ 24	τ ср
1				10	11,73	12,07	…	11,73	10,8616
2	+			12,17	14,23	14,65	…	14,20	13,2674
3		+		9,51	11,22	11,49	…	11,15	10,4004
4	+	+		11,71	14,04	13,62	…	13,62	12,6663
5			+	10,10	12,07	12,54	…	12,15	11,1516
6	+		+	12,44	14,96	15,31	…	14,89	13,6875
7		+	+	9,55	11,76	12,10	…	11,52	10,6628
8	+	+	+	11,92	14,68	15,0	…	14,52	13,2525

Так как все коэффициенты влияния – результат усреднения соответствующих сумм [7], их распределения нормальные, и может быть построен прогноз относительно экстремальных значений распределения (вmax, вmin), а при количестве опытов, приближающих соответствующие коэффициенты к крайним элементам, возможно заключение о достаточности повторов.

Если использовать такой путь оценки необходимого информационного обеспечения, то в качестве индикаторных выборок следует выбрать те, в которых отклонения в сторону ограничений максимальны. В случае УЗС это оказались образцы 3 (15,31 с – опыт 6) и 1 (9,51 с – опыт 3). То есть, это те совокупности факторов (худшие условия), которые провоцируют максимальное отклонение

П ои (т з ) от нормы. Также необходимы оценки, насколько условия выделяемых опытов вероятны при эксплуатации ОИ.

Таблица 3

Изменение коэффициентов влияния в i от количества k исследуемых образцов УЗС

k в i	8	16	24	в ср при k = 24
в о	11,9958	11,9969	11,9934	11,9925
в 1	1,2414	1,2374	1,2346	1,23
в 2	-0,2508	-0,2434	-0,2482	-0,25
в 3	0,2058	0,2057	0,1948	0,195
в12	-0,061	-0,016	-0,011	-0,015
в13	0,0586	0,0549	0,05137	0,055
в 23	0,0261	0,0299	0,01763	0,018
в 123	0,0211	0,0254	0,01796	0,028

Том 5 восстановления таких результатов, используя существующий массив измерений в «сомнительных» и смежных условиях.

Для ответа на вопрос можно использовать следующие математические предпосылки.

Пусть с некоторой выборкой ОИ ( к ) реализован ПФЭ. Результаты отражает совокупность факторограмм (коридор откликов) на рис. 3.

Так как все ОИ, подвергнутые ПФЭ, идентичны, изготовлены в условиях одного производства, по одному техпроцессу, на однотипных комплектующих и испытаны в одинаковых условиях (при одних и тех же наборах уровней воздействий), к ним применим принцип Седякина [9; 10]: параметры изделия однозначно определяются наборами внутренних параметров и временем П( x , t ) и, независимо от предыстории, будут изменяться значения П_ои в разных режимах по одинаковому закону.

Из этого следует, что:

• 2.3.    Применение принципа Седякина

При исследовании УЗС разработчики сталкивались с ситуациями, когда по разным причинам появлялись сомнения в результатах отдельных опытов или эти результаты отсутствовали. Возникал вопрос о возможности уточнения или

П ОИ

• •    отклонение параметра в условиях опыта £ i от средневыборочного значения П_ср(е i ) обусловлено разбросом параметров комплектующих (внутренние факторы), реализующих данный ОИ (рис. 3);

• •    закон плотности распределения П_ои ρ(П) одинаков по всем направлениям факторного пространства (опытам).

  П _max (Ԑ _i ) П (Ԑ _i ) П ср (Ԑ _i )

  
  

  П _max (Ԑ _j )

  П (Ԑ _j ) П ср (Ԑ _j )

  
  

ρ ( П )

N

Ԑ i

Ԑ j

Рис. 3. Фрагмент факторограммного коридора откликов

Тогда, если П(ε _i ) – результат испытаний ОИ в ε _i -х условиях, П(ε _j ) – искомое значение П_ои в ε _j -х условиях, П_ср(ε _i ) и П_ср(ε _j ) – средние значения П_ои в условиях ε _i -х и ε _j -х, а П( x_i ) и П( x_j ) – значения П_ои при тех же условиях, то для всех П( x_i ), которые П ср (ε i ) ≤ П( x i ) < П(ε _i ), вероятность

P {П ср (ε i ) ≤ П( x i ) < П(ε i )} = P {П ср (ε j ) ≤ П( x j ) < П(ε j )}.

Но,

^{Пср(£,) < П(X,) < П(£,)} =

П( 6 / )

= j Р(П) dnj 8,=Р(П)/£,[П(£,) - Пср(8,)],

П ср (А)

где Р(П)/е,. - некоторое значение плотности распределения Пои в рассматриваемом промежут- ке, исходя из теоремы о среднем значении [4]. Аналогично для соответствующей вероятности в условиях εj-х.

Тогда, перейдя к интервалам П_ср(ε _i ) - П(ε _i ) и П_ср(ε _j ) - П(ε _j ), можно записать:

р(П)/8,[П(8,) - Пср(8,)]   =

Р(П max )/8,[Птах (8,) — Пср(8,)]

=   Р(П)/8У[П(8У) - Пф(8у)]

Р(Птах )/8,[П max (8,) - Пф(8у )]

и         р(П)/ 8      Р(П)/ 8j        +

i =             = const

Р(Пmax V 8 Р(Пmax V 8j при сохранении закона распределения в сечениях (условиях) εi-х и εj-х.

Тогда

П(е,) - ПСр(е,)     П (j - ncp(8j)

Птах (е,) - ПА) П™^) - ЩА)’

П(£j) = ПСр (£j) + [П(е,) - ПСр (е,)]R(г ^ j), где ΔП(εi) = П(εi) - Пср(εi) – приращение Пои в условиях  е i,  обусловленное  совокупно стью неварьируемых внутренних факторов; ΔП(εj) = П(εj) - Пср(εj) – приращение Пои в условиях еj, обусловленное теми же причинами; П£.) - расчетное значение П(еj) по результатам смежных опы-

^Птах ( ^Е j ) ^Пср ( ^Е j ) тов; R(i —— /) =---------------- - масштабный

П тах (^) ~ ПА) коэффициент перерасчета результатов опытов при исходе условий ε _i -х в условиях ε _j -х (рис. 3).

Тогда П (_£ / ) = П ср (8 / ) + ЛП( е i ) R (/ — j ) - расчетное значение недостающего П_ои по результатам смежных опытов.

Однако рассмотренный подход оказался недостаточно эффективным для практических применений. Во-первых, при малых выборках Пср(εi) и Пср(еj) «неравнопрочные». Если Пои в еj-м опыте необходимо рассчитать, то Пср разных опытов рассчитаны при разном количестве результатов, и это различие вносит погрешность определения П(£/ ). Во-вторых, полученный единичный результат не решает проблему сокращения количества опытов при экспериментальной отработке.

• 2.4.    Применение метода толерантных пределов

Более эффективным оказалось применение метода толерантных пределов с постепенным сближением экспериментальных результатов и расчетных толерантных оценок [4; 11].

Так, пусть для рассмотренного УЗС получены результаты испытаний 8 + 8 + 8 = 24-х образцов, отраженные качественно на факторограммном коридоре откликов (рис. 4).

Рис. 4 отражает поведение П_ои в факторном пространстве, а также те условия, которые обуславливают максимальные отклонения от П_ср (T _min - 3-й опыт, T_max - 6-й опыт). Это позволяет:

• •    выделить указанные опыты (условия), как потенциально «худшие» условия при увеличении количества испытуемых образцов;

• •    не повторять при дальнейших испытаниях ПФЭ, а испытывать новые реализации УЗС только в условиях опытов 3 и 6 (два опыта вместо 8).

  
  
  
  
  

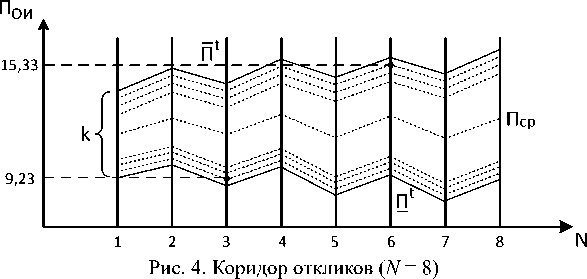
Для этих опытов при k = 8, 16, 24, ρ = 0,95, γ = 0,95 приведены расчетные величины Пср, S(П), П t, П t, kt (расчетные, табличные), где t Пои

П ср = А

Пt = Пср ± ktS(П);

S (П) – оценка среднеквадратичного отклонения в к измерениях (8, 16, 24); k - толерантный коэффициент (табулированный); П_ср - среднеквадратическое значение П_ои для k образцов ОИ (8, 16, 24) в опытах 3 и 6; П ^t и П ^t – толерантные пределы отклонения П_ои (нижние и верхние соответственно).

В табл. 4 отражены результаты опыта 3, в табл. 5 - опыта 6, в табл. 6 - расчетные величины параметров.

Приведенные расчетные данные и результаты экспериментов показывают, что с увеличением количества опытов экспериментальные данные и результаты прогнозов сближаются. И, исходя из условий применения и жесткости требований (выбор уровней ρ и γ), используя представленные данные, у экспериментатора достаточно материала для принятия решения.

При этом следует отметить также возможность сокращения количества опытов по последующим соображениям. На первом этапе испытывают 4–6 образцов ОИ, чтобы выяснить вариации Пои в пространстве варьируемых факторов и установить те наборы сочетаний уровней воздействий, которые вызывают максимальные отклонения Пои от Пср в обоих направлений. В случае УЗС это 3-й и 6-й опыты. Таким образом, дальнейшее исследование (до 24-х ОИ) уже отражено 2-я, а не 8-ю опытами с каждым УЗС (40 опытов вместо 160).

Том 5

Min (опыт 3)

Таблица 4

16	8	9,51	9,23	9,85	9,55	11,22	10,88	11,49	11,15
		11,16	11,5	10,9	11,2	9,56	9,81	9,23	9,49
		11,22	9,56	9,85	9,22	9,5	11,89	11,49	11,15

Таблица 5

Max (опыт 6)

16	8	12,44	12,14	12,82	12,57	14,96	14,51	15,32	14,87
		12,53	12,81	12,09	12,43	14,83	15,33	14,50	14,93
		14,89	15,31	14,47	14,90	12,53	12,82	12,08	12,41

Таблица 6

Расчетные величины параметров (опыты 3 и 6)

k Парам.	Min			Max
	8	16	24	8	16	24
П ср	10,36	10,4225	10,4004	13,72	13,6813	13,6763
S (П)	0,8323	0,8849	0,9118	0,9598	0,9961	1,0708
kt	2,350	2,174	2,108	2,350	2,174	2,108
П t	8,4040	8,4787	8,4753	–	–	–
П t	–	–	–	15,9755	15,8468	15,9335

Еще один существенный аспект для технологического процесса экспериментальной отработки. Для реализации испытаний на необходимом количестве образцов ОИ нет необходимости увеличивать их воспроизведение. Это привело бы к значительному расходованию ресурсов (время, финансовые затраты, материалы). Так как фактор конструкции практически отсутствует в составе внутренних факторов, замена функционально значимых элементов по плану разработчика ОИ позволяет минимизировать эту составляющую экспериментальной отработки.

• 2.5.    Применение бутстреп-метода

Первая публикация, посвященная бутстреп-методу, привлекла внимание инженеров-практиков, связанных с проектированием и экспериментальной отработкой новой техники [12; 13]. Казалось, что накопление статистического массива, который формируют эксперименты с ОИ, мож- но будет минимизировать, используя возможности современных ЭВМ.

Сущность метода заключается в следующем. Используя переходную выборку, например, результаты испытаний 8-ми образцов УЗС, с помощью ЭВМ продуцируется достаточно большое количество копий (например, 10⁹), которые тщательно перемешиваются, и из полученного макромассива случайным образом извлекают выборки, эквивалентные исходной (выборке бутстрепа), которые далее используют как результаты натурных экспериментов. В случае с УЗС это результаты ПФЭ с k образцами ОИ. Схема реализации бут-стреп-метода представлена на рис. 5.

Однако, метод не нашел широкого использования в инженерной практике. Главная причина заключалась в том, что, как отмечалось, результат НЭО – накопление достаточного массива экспериментальных данных для объективного информационного обеспечения разработки. А бутстреп-метод новой информации не получает, манипулируя полученными ранее данными.

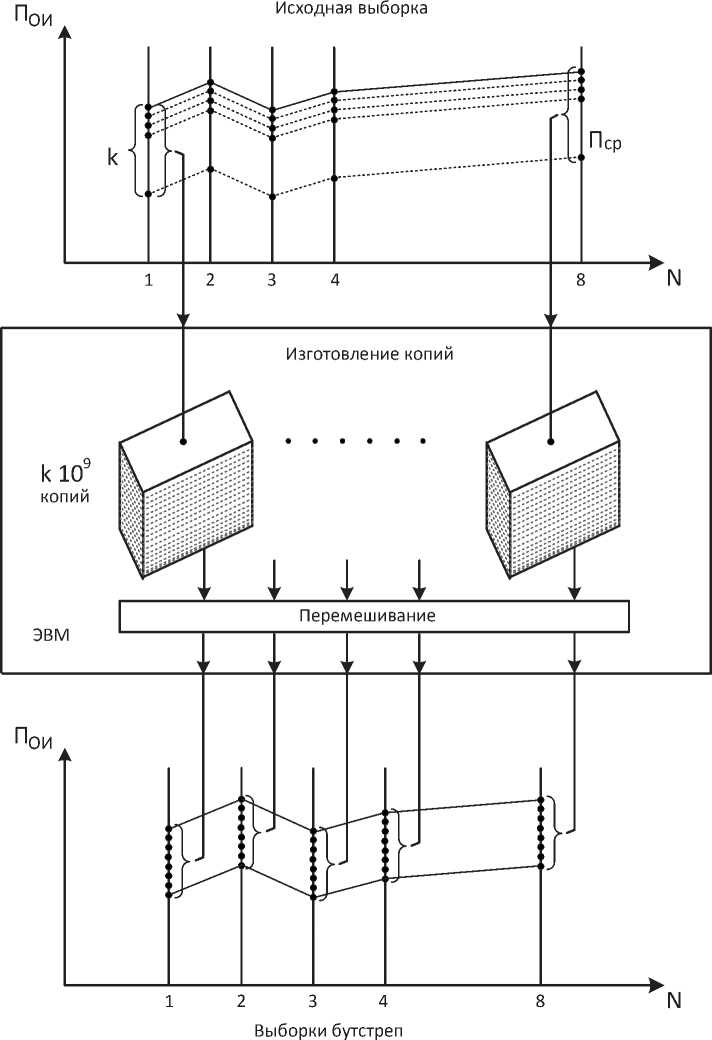
Рис. 5. Схема реализации бутстреп-метода

Заключение

Информационное обеспечение разработок БА КА является важнейшей составляющей технологии НЭО. Оно определяет необходимый уровень экспериментальных и исследовательских работ на этапе НЭО элементов БА и необходимый объем результатов для принятия решения о возможности использования разработок для эксплуатации в реальных условиях при воздействии комплекса ФКП в их естественном проявлении.

На различных этапах развития космической отрасли технология НЭО постоянно совершенствовалась. На современном этапе совер- шенствования и оптимизации экспериментального исследования элементов БА в инженерной практике стало возможным использование методологии МПЭ, позволяющей контролировать изменение параметров элементов БА при воспроизведении комплекса ФКП в наземных условиях и проводить анализ и обработку статистических данных для получения рекомендаций по дальнейшему улучшению эксплуатационных характеристик разработок. Применение МПЭ при НЭО элементов БА показало значительные возможности метода для совершенствования технологии и повышения качества наземной отработки [14–16].

Том 5