Эволюции во вращательном движении динамически асимметричных космических аппаратов в атмосфере

Самарский государственный аэрокосмический университет

Рассматривается нерезонансное движение динамически асимметричных космических аппаратов (КА) в атмосфере. Малая асимметрия этих аппаратов включает массовую, аэродинамическую и инерционную. При совпадении двух частот в системе уравнений движения КА может произойти реализация длительного резонанса, который приводит на практике к увеличению угла атаки до недопустимо больших величин. Основное внимание в работе сосредотачивается на изучении нерезонансных эволюций вращательного движения аппарата, вызванных влиянием резонанса. Эти явления известны как вторичные резонансные эффекты. Их исследование производится по усредненным в нерезонансном случае уравнениям движения КА. Аналитическое исследование вращательного движения динамически несимметричного аппарата сопровождается численными расчетами, результаты которых приводятся.

Несмотря на значительное число работ отечественных и зарубежных ученых по проблеме резонансов и их устойчивости при движении неуправляемого КА в атмосфере, в настоящее время некоторые вопросы остаются мало изученными. В частности, это относится к вторичным резонансным эффектам и связанной с ними внешней устойчивостью резонансов. Данные явления изучались также в работах Ю.А. Садова при рассмотрении двухчастотных систем с медленно изменяющимися переменными [1]. Кроме того, при анализе устойчивости главного резонанса в работе [2] Заболотновым Ю.М. было обнаружено нарастающее вращение КА с малой массовой и аэродинамической асимметриями (динамически симметричный аппарат) в атмосфере. Удалось показать [3], что указанное вращение аппарата вызвано влиянием вторичного резонансного эффекта. В представленной работе исследуется влияние вторичных резонансных эффектов на эволюции угловой скорости и угла атаки при движении динамически асимметричного КА в атмосфере.

В качестве исходных уравнений движения КА рассматривается нелинейная “низкочастотная” система, полученная из полной нелинейной системы с помощью известного асимптотического метода [4]. Кроме того, можно показать, что данные уравнения можно получить методом интегральных многообразий [5]. Она существенно проще исходной системы и описывает эволюции во вращательном движении КА в атмосфере. Эта система имеет следующий вид:

dωm

—- = - e    sin( 9 + 9 2) + dtI m^to2о sin2 a

+ e-----1,2-------cos(29 + 293)

Ix da      2m Atoato1 2 sin a

— = - e--------;x dt           Fa

ω1,2 sin α

2ωa cos(29 + 293) -

—

e 2m toa cos(9 + 9 ) +

F a             ¹

_{+ e 3} 4 m _z„ to g² SL

IF a    ^{q ,}

dθ

— = ^to x ^— to i,2 co^{s a} .      (3)

Здесь ε – малый параметр, характеризующий величину малой асимметрии аппарата и медленность изменения параметров движения центра масс ( q = dq / dt = O ( e ³ ) -при входе в атмосферу влияние изменения скоростного напора на угол атаки слабее влияния асимметрии), ω _x – угловая скорость КА относительно продольной оси, a = а п - пространственный угол атаки, 9 = ф п — п /2 , ф _п - аэродинамический угол крена, m A , m A , m ^A - обобщенные параметры асимметрии,

mA = 4(mA) + (mA2) , xx  x

mX1 = — cy 1 Ayto2tga / mzn ,

mX2 = — cy 1 Ato2tga / mzn ,

sin 92 = — mA / mA,

cos 92 = mA2 / mA,

mA = -J(mA) + (mA) ,

mA = —(mф — cx 1 Az)to 2tga / mzn , mA = —(mz + cx 1 Az)to 2tga / mzn, sin 91 = mA / mA, cos 91 =— m2 / mA,

mA = V(Iyz)2 + (AI)2 ,

sin 293 = AI / m A, cos 293 = — I yz / m A,

Az = Az / L ,

A y = A y / L - массовая асимметрия, m^ф _y , m _z ^ф – аэродинамические коэффициенты асимметрии формы,

I = (Iy + Iz )/2                        ,

AI = (Iz — Iy )/2, AI =AI /1, Iyz = Iyz / I

– динамическая асимметрия, сx1 , cy1 , mzп – коэффициенты лобового сопротивления, подъемной силы и восстанавливающего мо- мента, to12 = (Ixtox /2 ± toa )/cos a -частоты “прямой” и “обратной” прецессий, 22

to a = V I x to_x /4 + to , ^to = ^{— m} zn 4 ^SLct g ^a / I , q

– скоростной напор, S и L – характерные размеры

аппарата, mαzпqSL    2

F„ =---+ to 9 — 2tonto) i cos a .

a             _I           1,2 a 2,1

В уравнениях (1)-(3) учитывается главный резонанс, которому соответствует условие: to x — to 1 2 cos a = 0 . Главный резонанс оказывает наибольшее влияние на эволюцию медленных переменных по сравнению с резонансами высших порядков. Из решения последнего уравнения находится резонансное значение угловой скорости ω x ^r :

r ω _x ^r

л) 1 — I x

Знак в выражении (4) совпадает со зна- ком угловой скорости ωx .

Система (1)-(3) является стандартной системой для применения метода усреднения. Она относится к классу систем с несколькими медленными переменными и одной быстрой фазой θ . В стандартной форме она имеет следующий вид:

z= = sZ (z, 9, s)

dt , , , dθ

— = to(z). dt

Здесь z = {tox, a} - вектор медленных переменных,         to(z) = tox — ^12,

Z ( z , θ , ε ) – вектор-функция правых частей уравнений (1) и (2).

Усредняя систему (5)-(6) по быстрой фазе в нерезонансном случае (окрестность резонанса to x — to i 2 = о (^) )можно по-

лучить уравнения описывающие эволюцию медленных переменных:

три типа асимметрий, однако, сочетание массовой и аэродинамической асимметрий таково, что обобщенный параметр m ^A =0 .

Рассмотрим подробнее эти два случая.

Первый частный случай. Усредняя уравнения (1) и (2) на нерезонансных участках движения КА с учетом первых трех приближений метода усреднения при m x =0, получим:

o

— = eA1( zo) + e 2 A 2( zo) + dt

+ e3 A3 (zo ) + ...,

(7) где функции A _i , i =1,2,3,... – находятся с помощью известного метода [6].

Усредним систему (5)-(6) на нерезонансных участках движения с учетом высших приближений. Для описания нерезонансных эволюций, связанных с резонансом, во вращательном движении динамически симметричного КА достаточно учесть первые два приближения метода усреднения [3]. Причем эволюции проявляются во втором приближении (при нулевом первом приближении) и являются результатом действия возмущающих моментов от сочетания массовой и аэродинамической асимметрий.

При усреднении системы (1)-(3), влияние инерционной асимметрии на нерезонансные эволюциях системы определяется членами третьего приближения метода усреднения. При этом первые два приближения должны быть равны нулю.

Анализ усредненных уравнений для динамически несимметричного КА показывает, что здесь возможны два частных случая по сочетаниям действующих возмущений.

Первый частный случай. Имеется аэродинамическая и инерционная асимметрия, а массовая асимметрия отсутствует, т.е. m _x ^A = 0.

Второй частный случай. Имеются все

+

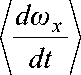
m ^A f ₂ f ₃

A ³

x (A

—

^A m f ₃

Af df^ ^{d ( m f} 3^) о a

A2       da

- A dA d(m f3~) _______о a + da

dA f d a da

+

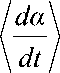
3(m f3)2 x

A ⁴

—

(saA 2

)rx

.f 2

Vd a 7

mA cos[2(9л — 9.)]

x------^---—,     (8)

8

= e ³

m ^A f ₃ f ₁

A ³

d , —a dA —a d ² A —^{( m f} 3) — ^{— m f}3—^ da da d a

mAf3 5 (mAf3A)dfl + oa

A3  da

+ 71 Г(m f3) A2 Lda       J

^mA^f 2 ^d f 3 _x A ³    9 to x

d —a      —a dA x - (m f3)A + 2 m f3^-da                 da

—

(m )2 f3 дf 1 дf; +

А ²     д а д а

If81 > f7 + А 8':---------- mA cos(29 1 - 293)

, 10)

+ (mA)2f32 дА 2А4    д tox

+

(m A)2 f32

2А ⁴

где

f2

дА     дf27 Л4А -22 +

² д а      д а

2А 2

д а¹

—

А 2 (д а )

> х

х m А cos[2(9 1 - 93)]

8

^{+ 8} 3 ^f 13 .

2ωaω1,2 sin α

F a

2    ■ 2

ω1,2 sin α

I x

,

^f 13 =

4 m zп ω a ² SL q

IFa       .

.   mAf3 д . —а   дf2

где ^f 5 = —5“   ^{( m f} 3 ”) ⁺

А ²   д а       д а

+

^{3( m}A^f 3 ^{) 2 f} 2 ГдА) ²

f 6 =

А ⁴

V д а )

— А „ „ m ff д . —а дА.

--^2^- — (m f 3—) +

А ³    д а       д а

ω12,2 sin 2

(tox +-- x

2 ω _a

α

) ,

+

3(m fз)2 дАдf2

А ³     д а д а

2 ω _a ω ² F a

^f 7 =

—

m A f₃ д , —а   д f_x

—— (m f3) — +

А ² д а        д а

,

+ f Т ( m f 3 )

А2 Ьда       _

—

Из уравнений (8) и (9) следует, что скорости эволюций медленных переменных ω _x и α в данном частном случае прямо пропорциональны величинам обобщенных параметров асимметрии. Кроме того, резонанс А = 0 приводит к этим эволюциям посредством вторичных резонансных эффектов, поскольку, все члены уравнений (8) и (9) содержат в знаменателях расстройку частот А .

Из уравнений (8) и (9) следует, что характер эволюций переменных ω _x и α относительно резонанса А = 0 определяют также выражения, стоящие в этих уравнениях в фигурных скобках. Так, при выполнении условий (10)

I f61 >1 f51,

-

-

mAf2 дf3 Г д z-А

А2 д tox

(m f3) да

(m )2 f3 f дf; +

А ²     д а д а

+ (mA)2f32 дА

2А4    д tox

+

(mA)2f32

А ⁴

f 8

-

а ²

д а¹

A m f3f1  д

А ³

дА да

—

+

f ГдА) 2

2(д а ) •

J / А f а дА

(m f3) да       да

—

• -а 8 ² д) ( m^f 3 ) ² ада f 1

• — m f 3

da 2 J     Д3    da da

mAh df3 Г.—a , ЭД"

• 2       2 m f 3 -

• Д3 d tox L d a _

• - 2( m A ) ² f 3² jAj f ■

Д3     dtox L da _ резонанс д = 0 сохраняет тенденцию свое- го влияния на переменные ωx и α в пределах нерезонансных участков движения (“притягивает” их к себе или “отталкивает” от себя) вне зависимости от того, с какой стороны по отношению к нему происходит эволюция (д >0 или д <0).

Напротив, при выполнении условий (11)

I f 5| >1 f 6|.

резонанс д = 0 “притягивал” значения угловой скорости ra x ( ro x ^ ю ^ на нерезонансных участках), то при д <0 он будет “отталкивать” значения ω _x и наоборот.

На рис.1 представлены эволюции медленных переменных ωx и α , вызванные влиянием резонанса д = 0 в данном частном случае. Кривая 1 на данном рисунке показывает изменение со временем резонансных значений угловой скорости ωx . Кри- вые 2 и 3 описывают поведение, соответственно, усредненной и не усредненной угловой скорости ωx , а кривые 4 и 5 – определяют изменение усредненного и не усредненного угла атаки α .

Из рис.1 следует, что усредненные значения данных медленных переменных, качественно, повторяют эволюции этих переменных до их усреднения. Кроме того, на рис.1 прослеживается увеличение скорос-

If7 I >

^f 8 +

8 f 13

m д cos(29 1 - 293)

влияние резонанса д = 0 на эволюцию пе-

ременных ω _x и α определяется тем, с какой стороны по отношению к нему происходит эволюция. Например, при выполнении первого условия (11). если при д >0

ти изменения переменных ω _x и α при приближении к резонансу д = 0 . Такое поведение медленных переменных характерно при вторичных резонансных эффектах.

Второй частный случай . Аналогично, усредняя уравнения (1) и (2) на нерезонансных участках движения КА с учетом первых трех приближений метода усреднения при m ^A = 0 получим:

-1

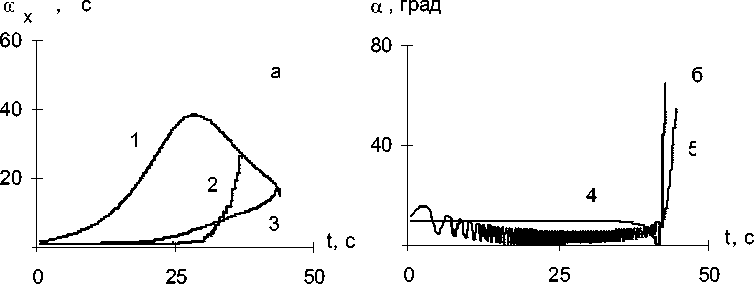
Рис. 1. Эволюции медленных переменных ω x и α :

Исходные данные для построения - m ^ m^д = 0 005 , 2 9 2 — 2 9 3 = 0 .

——) = s3(mx )2 m Л cos[2(6^ - 63)] х dt                             2     3

f 4 дЛ 16Л ⁴ д а

+

16Л ⁴

7 д\ д гох

f . - 4 л д ^ _х

+

Из уравнений (12) и (13) видно, что скорости эволюций переменных ω _x и α прямо пропорциональны обобщенному параметру асимметрии A ²

I т х I т ^Л cos(2 ^ 2 - 2 ^ 3 ) .

2Л 2

д ^ _х

( дЛ

—

f 42    д

8Л ³ дго —

^{д ю}х )

дЛ f2 д гох

^da\   3/^— A _а2 Л

— ) = s (т х ) m dt

х <

f 4² f 1

8Л ⁴

+

f 4²

8Л ³

f ₂

—

cos[2( 6 ₂ - 6 3 )] х

д2 Л    / дЛ )

--7Л-3 V-д го _х ²       (^{д го}х )

3 дЛ д f 1 д го _х д го _х

—

Ц Л д го _х

+

^ +

+ s

4 m zп ω a ² SL q

IFa       ,

ω ²

где ^f 4 = у^- I x

.

Уравнения (12) и (13) описывают эво-

Характер поведения этих медленных переменных относительно резонанса Л = 0 определяют также выражения, стоящие в фигурных скобках в уравнениях (12) и (13). Например, при выполнении условий (14)

If9I < |f101,

f 11

f ₁₀

f ₁₁

+            8 f L3

m ^Л ( m х ) ² cos(2 6 2 - 2 6 3 )

где f 9

+ 2Л ²

f 4²

2Л ⁴

д ² f 2

д го_х²

<1f121,

7 _дЛдЛ f + дгох да 1

( дЛ

-

(дЮх )

f ₂

f42Г2 дf1 дЛ + ^Г^Л f

А ³     д го_х д а д го_х д го_х²

x   xx

f 4²

Л ²

д ² f , д го _х

+

f 4² f 1

Л ⁴

I дЛ I

(дЮх )

люцию угловой скорости ωx и угла атаки α в случае mA =0 на нерезонансных участках движения, вызванную влиянием главного резонанса Л = 0• Это следует из вида данных уравнений, которые содержат в знаменателях своих правых частей резонансные расстройки частот Л • При приближении к резонансу Л уменьшаются, поэто- му скорость эволюций переменных ωx и α увеличивается. Так проявляют себя вторичные резонансные эффекты.

f 4² f 1

Л ³

д 2 Л д гох 2

^f [’

дЛ д f 1 д го _х д го _х

резонанс Л = 0 сохраняет тенденцию свое- го влияния на переменные ωx и α в пределах нерезонансных участков движения (“притягивает” их к себе или “отталкивает” от себя) вне зависимости от того, с какой стороны по отношению к нему происходит эволюция (Л >0 или Л <0).

Напротив, при выполнении условий

I f 9I >  I f 10 I,

I f 111 >

f 12 +

8 f 13

m д (m x )2 cos(292 - 293)

oai aa^ oey aёёy^ ey da^T ^ а^ па д = 0 на изменение переменных ω _x и α зависит от того, с какой стороны по отношению к нему происходит эволюция. Например, при выполнении условия (16), если при д >0 резонанс д = 0 “притягивал” значения угловой скорости to x ( ^ x ^ ro x на нерезонансных участках), то при д <0 он будет “отталкивать” значения ω _x и наоборот.

На рис.2 показываются эволюции медленных переменных ω _x и α , вызванные влиянием резонанса д = 0 .

Обозначения кривых полностью соответствует обозначениям рис.1.

Из рис.2 также следует, что эволюции усредненных значений медленных переменных ω _x и α повторяет качественно эволюции этих переменных в не усредненном случае. С другой стороны такое изменение данных медленных переменных характерно для вторичных резонансных эффектов.

Исходные данные для построения

рис.2.12: mAmд = 0.007, 292 - 293 = п.

Таким образом, получены усредненные уравнения, которые позволяют изучить влияние различных сочетаний массовой, аэродинамической и инерционной асимметрий на движение динамически несимметричного ТТ относительно центра масс. Эти уравнения позволяют сформулировать некоторые новые условия, отражающие особенности влияния резонанса на эволюции медленных переменных при движении динамически несимметричного ТТ в атмосфере.