Эволюция характеристик решений двумерных уравнений идеальной пластичности
Автор: Сенашов Сергей Иванович, Гомонова Ольга Валерьевна
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Математика, механика, информатика
Статья в выпуске: 3 (16), 2007 года.
Бесплатный доступ
Известное решение Прандтля преобразовывается точечными симметриями. В результате получены новые классы точных решений уравнений пластичности. Подробно рассмотрены те решения, которые могут быть использованы для описания плоских течений, возникающих при сжатии пластического слоя жесткими плитами.
Короткий адрес: https://sciup.org/148175558
IDR: 148175558 | УДК: 539.374
Текст научной статьи Эволюция характеристик решений двумерных уравнений идеальной пластичности
Рассмотрим систему дифференциальных уравнений пластичности [1] вида
оx - 2к(6x cos 26 + 6у sin 26) = 0,
о у - 2 к (6 x sin 26 - 6 y cos 26) = 0, где о - гидростатическое давление, 6- угол между осью Ox и первым главным направлением тензора напряжений, к - постоянная пластичности; нижний индекс означает дифференцирование по соответствующей переменной.
Для этих уравнений группа преобразований известна [2]. Она порождается следующими операторами:
X =d x , Х 2 =д у ,
Х 3 = x d x + У д у , Х 4 = - У д x + х д у +д 6 ,
X 5 = д ° , Х б = ^д x +^ 2 д у - (2)
-46kда-^д0, Х+=^дx +пду, k где ^i = x cos 26 + у sin 26 + у —, <2 = x sin 26 - у cos 26 - x —;
1 k 2 k
( ^ , п ) - произвольное решение линейной системы
J^ 6 - 2 к ( ^о cos 2 6 + по sin 2 6 ) = 0 , [П 6 - 2 к ( ^о sin 2 6 - по cos 2 6 ) = 0 .
Для построения новых решений системы уравнений (1) используются преобразования симметрий, которые порождаются оператором X + из (2) и имеют вид x ' = x + a ^ ( a , 6 ), у ' = у + a п ( о , 6 ).
Для их построения необходимо знать точные решения системы дифференциальных уравнений (3). Несмотря на то, что эта система уравнений - линейная, построить точное решение, которое позволило бы получить хорошее преобразование, не так просто.
Приведем один из возможных способов построения точных решений системы (3).
Лемма. Система уравнений (3) имеет следующие решения:
cos 2 6 , — - sin 2 6 k
— + sin 2 6 , - cos 2 6 k
(^, По), (п + ^о,4 + ^),
4 к 6^о + — ^е +^ cos26 + n sin26 + n —, kk
,
4 к 6по + к П 6 + ^ sin2 6-n scos2 6-^ - ^ где ( ^ , п ) - произвольное решение системы (3).
Доказательство этих фактов получается из таблицы коммутаторов операторов (2).
Эта лемма дает возможность получить серию новых точных решений системы уравнений (3). Для этого нужно выбрать конкретное ее решение и подействовать на него любым из преобразований Т , Т 2 или Т 3 , где
Т2 :(S,П)>(п + ^о,-^ + П6),
Т 3 : ( 5 , П ) >
4 к 6^о + ° ^6 + ^ cos 26 + ° к
+Пsin26 + n°, 4к6по + °П6 +
+^ sin 26-п scos26-^a
Выберем в качестве «затравочного» очевидное решение системы (3): O = (1,0). Подействуем на него преобразованиями Ti, Т2, Т3. Получаем, соответственно, решения T1( O) = A = (0,0), T2( O) = B = (0, -1) и
T3 (O) = H1 = I cos 26, sin 26 - — . Из этих решений наи-V k J более интересным представляется последнее. Применим к нему преобразования T1, T2, T3. Получаем снова решения системы (3) ит. д.. Наиболее перспективным, по нашему мнению, направлением по построению новых решений является действие преобразованием T3 , а также различные комбинации преобразований T2 и T3. Этот процесс можно представить в виде «дерева» решений (рис. 1).
(вдоль которого выполнено условие
— Q С
--+6 — —
2 k 2 Л
Эти характеристики в теории пластичности являются линиями скольжения, т. е. линиями, вдоль которых действует максимальное касательное напряжение. Поле (5)-(6) образовано двумя ортогональными семействами циклоид с радиусом производящего круга, равным 1.
Графики первого (5) и второго (6) семейств характеристик приведены на рис. 2. График первого семейства характеристик показан на рисунке сплошной линией, график второго семейства - пунктиром (при построении было выбрано значение C = 0 ).
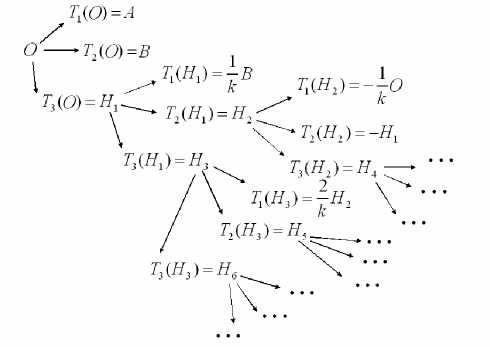
Рис. 1
3 1
2 -
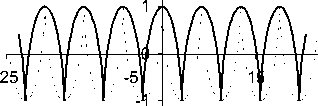
-2 -
-3 -
Рис. 2
Отметим некоторые из получающихся новые решений H i :
H = I cos 2 6 ; sin 2 6 - — | , 1 V k I
H = I - — - sin 2 6 ; cos 2 6 | ,
2 V k I
Как уже было отмечено, уравнения теории пластичности допускают группу точечных симметрий, которые переводят решения системы снова в решения этой же системы, а характеристики - в характеристики.
Рассмотрим, как одно из таких преобразований действует на характеристики решения Прандтля. Выберем преобразование вида
H 3 =
I — I — I
- 2 —sin2 6-I — | + 1;
k I k I
H =| cos 2 6 , sin 2 6 - —
1 V k
Подействуем этим преобразованием на характерис
.
- 4 6 + 2 — cos 2 6 k
Рассмотрим известное решение Прандтля системы уравнений пластичности (1):
— = - kx + k ^/1
- y 2, y = cos 26.
Решение Прандтля можно использовать для описания течения пластического материала при сжатии слоя этого материала между параллельными жесткими и шероховатыми плитами. Это же решение может быть записано в виде
тики (5) и (6). Получаем, соответственно x ‘ = - 2 6 - sin 2 6 + a cos 2 6 + C ,
y' = cos 26 + a I sin 26-— I I k I
и x' = 26 - sin 26 + a cos 26 + C, y '= cos 26 + a I sin 26-— I, V k J где C - произвольная постоянная.
— = - kx + k 4 1 - y 2,
6 = ± - arccos y + n n .
Решение (4) имеет два семейства характеристик, имеющих следующий вид:
x = - 2 6- sin 2 6 + C , y = cos 2 6 ,
Тогда параметрические уравнения преобразованных характеристик (с учетом соотношений 2 k - 6 = - у и
—+ 6 = - C , соответственно) имеют вид 2 k 2
x‘ = -26 - sin 26 + a cos 26 + C, y' = cos 26 + a (sin 26- 26 + C), (^)
— „ - C
(вдоль которого выполнено условие 2^ _ о - _ у ).
,
x = 2 6- sin 2 6+ C , y = cos 2 6 , (6)
и x‘ = 26 - sin 26 + a cos 26 + C, y ' = cos26 + a (sin26 + 26+ C). ^^
Найдем огибающие этих семейств характеристик. Напомним, что огибающей семейства кривых на плоскости называется кривая, которая в каждой точке касается одной из кривых семейства [3].
Рассмотрим уравнения характеристик (9). Необходимое условие существования огибающей:
Ф ( е , с ) =
x C x е
У с у е
= 0.
Имеем выражение
ф ( е , C ) = 2 a 2 sin2 e + 4 a cos2 e- 2sin2 e = 0.
То есть
a 2 sin2 e + 2 a cos2 e- sin2 e = 0 и tg2 e =---- —.
(1 - a 2 ) Таким образом,
1 . 2 a к
— arctg----— + — n np9 a * ±1,
2 (1 - a 2 ) 2
— + — n np9 a =±1
ниях параметра для данного семейства - линии возврата. При a > 1 наоборот, выражение (13) представляет собой уравнения линий возврата, выражение (14)-уравне-ние огибающих.
Проведя аналогичные рассуждения для второго семейства характеристик (10), получаем те же выражения (13) и (14) в результате поиска огибающей. Но в этом случае при a | < 1 уравнения огибающих имеют вид (14), а (13) представляет собой линии возврата для второго семейства характеристик. При значениях параметра a > 1 уравнения огибающих имеют вид (13), уравнения линий возврата-(14).
Построим графики характеристик первого семейства (9) и второго семейства (10) и огибающих для характеристик первого и второго семейств (рис. 3, 4) при различных значениях группового параметра a и при C = 0. Здесь сплошной линией показаны графики характеристик первого семейства и линий (13), пунктиром - графики второго семейства характеристик и линий (14).
Достаточным признаком существования огибающей является выполнение условия
А = ^ф' с - r c ^' e * 0, где r = ( x ( e , C ), у ( e , C ) ) .
Проверим выполнение достаточного признака:
А = - ( ( 4 a 2 - 4 ) cos2 e- 8 a sin2 e ; ( 4 a 3 - 4 a ) cos2 e- 8 a 2 sin2 e ) .
Достаточный признак выполняется, если q , 1 a а 1 -1. П e * — arctg--+ — n, n e Z.
2 2 a 2
Очевидно, что полученное значение для угла e из системы (11) удовлетворяет последнему условию. То есть огибающие рассматриваемого семейства характеристик существуют при различных значениях параметра a . Найдем их уравнения.
Исключим константу C из уравнений (9). Получим следующее равенство:
ax '- у ' = - 2a sin2 e + ( a 2 - 1)cos2 e . (12)
Подставив в уравнение (12) выражения для e из (11), получим
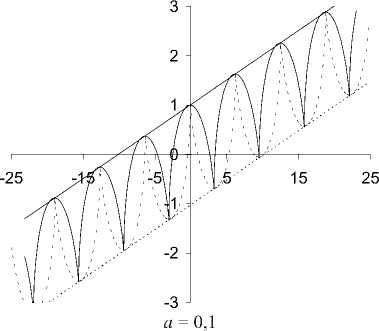
Рис. 3
ax - у = ’
? • ft 2 a )
- 2 a sin arctg-----— + кn ■
(1 - a 2)
+
( a 2 -
f n A
, 2 a . _ „ . ,,
1) cos arctg-----— + n n np9 a * ± 1, (1 - a 2)
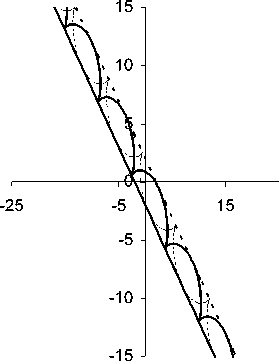
а = -1
Рис. 4
т 2 cos к n
np9 a = ±1.
Для четных значений числа n получаем у = ax + a2 +1, (13)
для нечетных значений n имеет у = ax - a2 -1. (14)
Рассмотрим еще одно решение системы линейных уравнений (3) вида
Выражение (13) представляет собой уравнение огибающих для первого преобразованного семейства характеристик (9) при a < 1 . Выражение (14) при этих значе
a ( e )sin + b ( e )cos
( 2 k J ( 2 k,
A ( e ) sin I — |+ B ( e ) cos I —
I 2 k I I 2 k
где функции a ( 6 ) , b ( 6 ) , A ( 6 ) , B ( 6 ) можно определить из решения соответствующих систем обыкновенных дифференциальных уравнений.
Выясним, как действует преобразование (15) на характеристики (5) и (6). Подставим (15) в систему линейных уравнений (3). В результате получим систему уравнений для определения функций a (6), b (6), A (6), B (6), имеющую вид a '(6) + b (6) cos26 + B (6)sin26 = 0, b ‘(6)- a (6) cos 26- A (6)sin26 = 0,
A '( 6 ) + b ( 6 ) sin2 6- B ( 6 ) cos2 6 = 0,
B '(6 ) - a ( 6 ) sin2 6 + A ( 6 ) cos 2 6 = 0.
Сделаем следующие преобразования: продифференцируем каждое из уравнений (16) по 6 , тогда с учетом уравнений (16) получим следующие системы уравнений:
+ (1 - 72)cos(1 + 72) 6
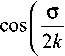
Теперь выписываем преобразованные уравнения характеристик (5) и (6). Получаем соответственно x' = -26- sin 26 + a I cos(1 - 72)6 sin I 6--
( r- r- ( C
- a I (1 - 72)sin(1 + 72) 6 cos I 6- -2 .
y ' = cos 2 6 + a sin(1 - 72) 6 sin I 6--+
I I 2 JJ
J I. C
+ a I (1 - 72)cos(1 + 72) 6 cos I 6--
I I 2 JJ для первого семейства характеристик и a '(6) + a (6)+ 2 A '(6) = 0, A '(6) + A (6)-2 a '(6) = 0
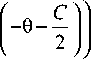
' b ‘ ( 6 ) + b ( 6 ) + 2 B '( 6 ) = 0, B '"( 6 ) + B ( 6 ) - 2 b ' ( 6 ) = 0 .
Будем искать решение системы (17): a ( 6 ) = Ce %6 , A ( 6 ) = De %6 , где C , D , %- постоянные.
Тогда для определения C , D , % получим следующие алгебраические уравнения:
C % 2 + C + 2 D % = 0,
x ' = 2 6 - sin 2 6 + a | cos(1 - 72) 6 sin
IJ
- a I (1 - 72) sin(1 + 72)6 cos I -6
1 r y' = cos 26 + a I sin(1 - 72)6 sin J -6+
. 2 JJ
C H 2 11
+ a I (1 - 72) cos(1 + 72 ) 6 cos I -6
для второго семейства характеристик.
Приведем графики характеристик (19) для различных значений параметра a (рис. 5, 6).
D % 2 + D - 2 C % = 0.
Из этих уравнений без труда получаем
C 1,2 = ± iD , % 1,2 = i (1 ± 72), i 2 =- 1.
В силу этого окончательное (действительное) решение системы (17) имеет вид a (6) = C1 cos(1 ± 72)6 - C2 sin(1 ± 72)6,
A ( 6 ) = C 1 sin(1 ± 72) 6 + C 2 cos(1 ± 72) 6 , где C 1 , C 2 - произвольные постоянные.
Тогда согласованное с ним решение системы (18), с учетом (16) запишется следующим образом:
b ( 6 ) = (1 ± 72) х х ( C 2cos(1=f72) 6- C 1 sin(1TT2) 6 ) , b ( 6 ) = (1 ± 72) х х ( C 2 sin(1=F72) 6 + C 1 cos(14=72) 6 ) . Для простоты и наглядности рассмотрим случай, когда C 2 = 0 , выбираем также всюду нижний знак, тогда (15) запишется в виде
£ = cos(1 - 72) 6 sin ( 2 ^ ^-
- (1 - 72)sin(1 + 72) 6 cos | — | , z 4 z I 2 k
П = sin(1 - 72) 6 sin I 2 k 1+
6 -1
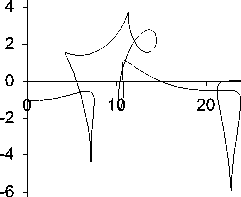
-8 J
а = 5
Рис. 5
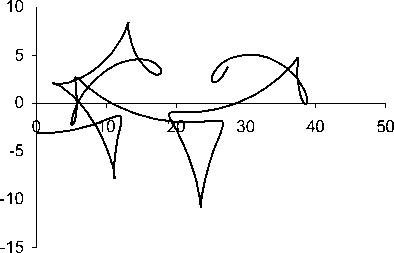
а= 10
Рис. 6


