Эволюция электростатической волны, распространяющейся перпендикулярно однородному магнитному полю в плазме
Автор: Долгоносов М.С., Кузичев И.В., Зеленый Л.М.
Журнал: Труды Московского физико-технического института @trudy-mipt
Рубрика: Физика, электроника, нанотехнологии
Статья в выпуске: 2 (10) т.3, 2011 года.
Бесплатный доступ
В данной работе численно изучено затухание Ландау ленгмюровских колебаний плаз- мы, распространяющихся перпендикулярно постоянному магнитному полю. В каче- стве численной схемы была выбрана схема расщепления. Показано, что эволюция волны носит бифуркационный характер, то есть при изменении значения некоторо- го управляющего параметра затухание волны прекращается (либо волна начинает затухать). В частности, если в отсутствие магнитного поля в режиме Ландау волна затухала, то по мере увеличения магнитного поля затухание волны предотвращается доминирующим воздействием магнитного поля. В режиме ОНейла влияние магнит- ного поля приводит к совершенно иному эффекту. Слабое магнитное поле уменьша- ет амплитуду осцилляций огибающей электрической энергии. Затем, при переходе через пороговое значение амплитуды магнитного поля, первоначально не затухаю- щая волна затухает на временах порядка гиропериода. Дальнейший рост амплитуды магнитного поля опять останавливает затухание волны и приводит к генерации берн- штейновских мод.
Короткий адрес: https://sciup.org/142185752
IDR: 142185752
Текст научной статьи Эволюция электростатической волны, распространяющейся перпендикулярно однородному магнитному полю в плазме
Интерес к процессу распространения электростатических волн в бесстолкновительной плазме не ослабевает уже более полувека с момента опубликования Л.Д. Ландау статьи [1], в которой он подробно рассмотрел случай незамагниченной плазмы и обнаружил затухание плазменных волн в линейном приближении. Впоследствии этот эффект был назван затуханием Ландау . На первый взгляд, возможность затухания кажется удивительной, учитывая, что бесстолкновительное кинетическое уравнение сохраняет энтропию.
Чтобы понять механизм затухания Ландау, рассмотрим движение электронов в электростатическом потенциале у ( E = —Vy ) плазменной волны, распространяющейся со скоростью v ^ вдоль оси x . Траектории частиц в фазовом пространстве схематически изображены на рис. 1 в системе координат, связанной с волной. Замкнутые траектории соответствуют частицам, захваченным в потенциальную яму волны. Частицы, находящиеся изначально в точках 1 и 4, при движении будут терять энергию в начальный момент времени, а частицы в точках 2 и 3, наоборот, увеличивать. Однако для функций распределений по скорости типа максвелловского (рис. 2) в точках 2 и 3 находится больше частиц, чем соответственно в 1 и 4 (см. рис. 2). Таким образом, энергия частиц в целом возрастает, что приводит к затуханию волны в силу закона сохранения энергии.
Первые результаты по затуханию плазменных волн получил Л.Д. Ландау. В отличие от Власова, ранее изучавшего проблему распространения волн в плазме, для решения линеаризованного уравнения Власова Ландау использовал преобразование Лапласа по времени, что не только позволило соблюсти принцип причинности, но и привело к обнаружению мнимой части продольной диэлектрической проницаемости плазмы, то есть затухания колебаний. Ландау получил, как и Власов, закон дисперсии плазменных волн, а помимо этого и декремент затухания. В случае слабого затухания, когда можно еще говорить о распространении волны, частота и декремент задаются следующими формулами:
2 _ 2 Л I 3Tek2 А ш = шр (1 +Г / ; p mω2
_ П шр 1 3
Y L = V8(kr De ) 3 exp к 2( kr De ) 2 - 2 .
Здесь T e — температура электронов, ш р = 4ne 2 n e /m e — квадрат плазменной частоты (электронной), r De = VТ е /т е /ш р — дебаевский радиус электронов, к — волновое число. Движением ионов для таких быстрых процессов можно пренебречь в силу их большой массы по сравнению с массой электронов. При выводе этих формул начальное распределение электронов по скоростям предполагалось максвелловским (рис. 2) [l].
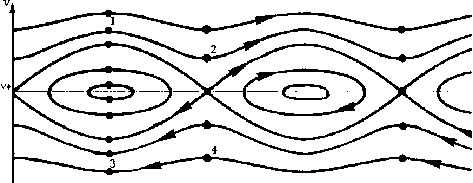
Рис. 1. Движение в фазовом пространстве
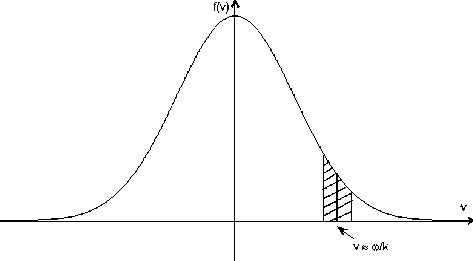
Рис. 2. Распределение электронов по скорости. Резонансная область заштрихована
На самом деле существует довольно сильная зависимость процесса затухания от начального распределения, связанная, в частности, с возможностью аналитического продолжения диэлектрической проницаемости в нижнюю полуплоскость комплексных частот.
Для ионного звука, существующего в сильно неизотермической плазме ( T ^ T e ), при учете взаимодействия с ионами также возможно затухание, а для электромагнитных волн затухания, конечно, нет, так как фазовая скорость электромагнитной волны в плазме превышает скорость света.
Результаты, полученные Ландау, верны лишь на временах применимости линеаризованного уравнения Власова. Естественно, возникает вопрос как в оценке этого времени, так и о дальнейшей эволюции волны. В 1965 году была опубликована статья O’Нейла [2], в которой подробно изучалась эта проблема. Оказалось, что характерным временем применимости ли неариз ованного уравнения является период колебаний электронов в потенциальной яме т ь = ^m/eAk (точнее, период, деленный на 2п ) волны с амплитудой A и волновым числом к . Понятно, что на этих временах основную роль играют частицы, захваченные волной (замкнутые траектории на рис. 1). Что касается дальнейшей эволюции волны, то автор обнаружил, что при некоторых условиях происходит переход в стационарный режим колебаний, то есть затухание прекращается. Это возможно, когда Y L T b ^ 1 , что означает слабое изменение профиля волны в линейном режиме затухания.
В работе О’Нейла были использованы несколько приближений, которые позже вызвали сомнения (впрочем, необоснованные) у некоторых исследователей затухания Ландау [3, 4], так как предполагалось, что профиль плазменной волны не изменяется, что, на первый взгляд, не согласуется с постановкой задачи — изучение колебаний в нелинейном режиме. Однако возможность такого приближения существует, как показал О’Нейл, при Y L T b ^ 1 , поскольку именно этот параметр определяет окончательную стационарную амплитуду волны.
Качественно объяснить переход в стационарный режим можно следующим образом. При описании линейного затухания мы учли, что электронов, в том числе и захваченных волной, которые отстают от волны, было больше, чем тех, которые ее догоняют. Таким образом, энергия волны передается частицам. Однако после отражения от потенциального барьера захваченные частицы, отстававшие от волны, теперь догоняют ее, и энергия передается уже волне.
Как следствие, декремент затухания в этом случае является осциллирующей функцией времени. Кроме того, следует учесть, что период нелинейных осцилляций в потенциальной яме зависит также и от энергии частиц (частота осцилляций нелинейного маятника ш(Е) ~ ша/K(^(E/шА + 1)/2), где ша = 1/ть, E — энергия частицы в системе волны, а K — полный эллиптический интеграл первого рода). В фазовом пространстве это будет выглядеть как перемешивание областей, занятых частицами. В итоге число частиц в обеих группах примерно выравнивается, и затухание волны прекращается. В терминах функции распределения усреднен- ную картину можно описать следующим образом: в резонансной области v ∼ vϕ , vϕ — фазовая скорость волны, функция распределения начинает выравниваться и возникает плато (рис. 3). В дополнение стоит отметить, что сама возможность существования стационарных волн в плазме исследовалась еще до О’Нейла в статье [5]. Авторы обнаружили существование незатухающих мод, которые являются решениями уравнений Власова–Максвелла (т.н. BGK-моды).
Как ясно из вышесказанного, возможны два режима эволюции волны (рис. 4). Первый, называемый обычно режимом Ландау, соответствует сильному затуханию на временах применимости линейного приближения. В нем волна полностью затухает. Второй режим — режим О’Нейла — реализуется, когда начальное затухание достаточно слабое, волна не успевает затухнуть до того, как нелинейные эффекты начнут играть существенную роль в процессе передачи энергии от волны
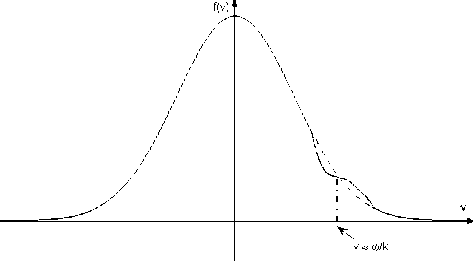
Рис. 3. Возникновение плато
к частицам. Затухание прекращается, и волна переходит в стационарный режим. В каком из двух режимов будет происходить эволюция волны, зависит от начальных условий. Этот вопрос подробно рассмотрен в статье Lancelotti and Dorning [6], авторы которой исследовали критические (в смысле перехода между двумя возможными случаями) начальные условия. Задача была сформулирована как бифуркационная. Электрическое поле разделялось на две части — кратковременную и долговременную. Авторы нашли такое начальное условие (начальное возмущение функции распределения), что для меньших возмущений реализовывался режим Ландау, а для больших — режим О’Нейла. Асимптотические осцилляции электрического поля наблюдались экспериментально, результаты изложены в работе Danielson et al. [7].
В связи с существованием стационарных волн возникает вопрос о способе перехода плазмы в состояние равновесия и о пределах применимости уравнения Власова при описании взаимодействия частиц и волны. В статье Carbone et al. [8] эта проблема изучалась с помощью мо- делирования плазмы методом частиц, то есть с некоторыми оговорками моделирование проводилось «из первых принципов». Основным результатом было наблюдение филаментации фазового пространства и расчет корреляционных функций. Оказалось, что взаимодействие волны с частицами порождает корреляции между частицами, которые уравнением Власова уже не описываются. По сути, при перемешивании в фазовом пространстве возникают мелкомасштабные осцилляции функции распределения, причем их размер становится все меньше и меньше. При достижении некоторой характерной длины (определяющей «дискретность» плазмы) этот процесс должен остановиться, но в уравнении Власова нет такой длины, следовательно, оно уже не пригодно для описания плазмы. Необходимо учитывать диффузию в пространстве скоростей, которая сглаживает эти осцилляции [9]. В этом случае энтропия растет, и, как следствие, процесс становится необратимым. Таким образом, переход к равновесию связан с филаментацией фазового пространства. Стоит отметить, что характерное время столкновений больше, чем время применимости уравнения Власова, определенное таким образом.
До сих пор мы рассматривали затухание Ландау в незамагниченной плазме. Если же плазма находится в постоянном внешнем магнитном поле, задача становится намного сложнее уже в линейном режиме. Наличие магнитного поля приводит к множеству интересных эффектов как математического, так и физического характера.
Рассмотрим плазму во внешнем постоянном однородном магнитном поле B 0 . Поскольку такая постановка задачи является более общей, чем предыдущая, то, безусловно, результаты должны в пределе B 0 → 0 совпадать с уже полученными. Однако, как было показано Бернштейном [10], электростатические волны, распространяющиеся перпендикулярно магнитному полю (т.н. моды Бернштейна, их частоты близки к nωB , где n — целое число, ωB — ларморовская частота), не затухают при любом конечном, пусть даже очень малом, B 0 . Физически отсутствие затухания для таких волн объясняется тем, что частицы движутся в магнитном поле по винтовой линии. Таким образом, частица, передавшая энергию волне, на другой части своей траектории заберет от волны какую-то часть энергии. Условие Ландау в магнитном поле выглядит следующим образом: ш = пшв + kzvz, то есть содержит лишь продольную компоненту скорости. Однако если в соответствующем дисперсионном уравнении сначала перейти к случаю Bо ^ 0, а затем рассмотреть случай 0 = п/2, то получается результат Ландау. Направление осей выбрано, как показано на рис. 5.
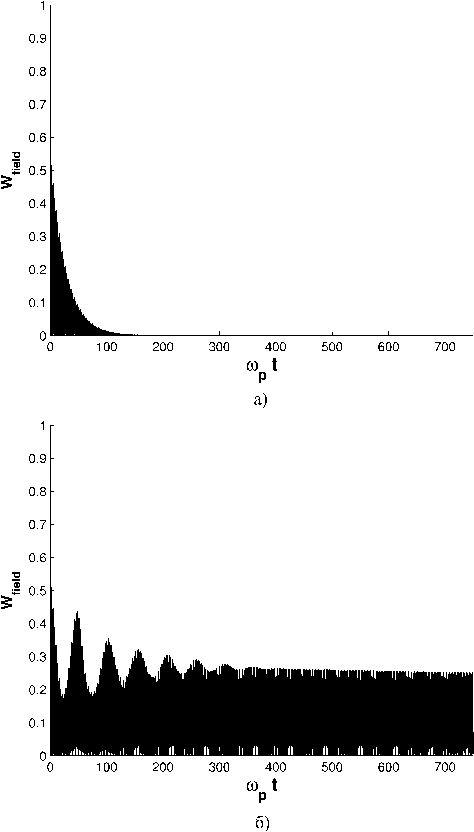
Рис. 4. Эволюция энергии ленгмюровской волны в режимах Ландау (слева) и О’Нейла. Под W f ield здесь и далее понимается нормированная на начальную энергия волны W field = W/W 0
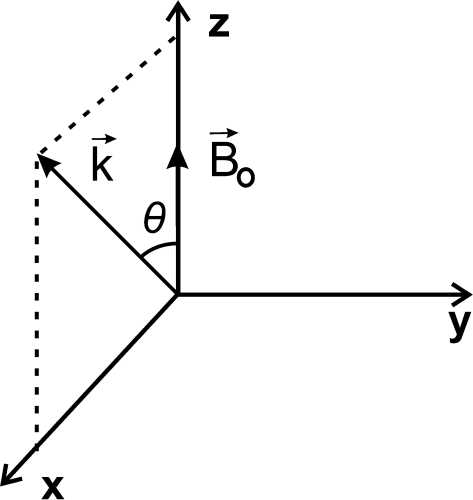
Рис. 5. Направление осей системы координат
Эта сложность с переходом к пределу B о ^ 0 представляет собой одну из наиболее интересных особенностей волн в магнитном поле, известную как парадокс Бернштейна–Ландау [10, 11]. Влияние слабого магнитного поля сводится лишь к появлению малой поправки к результату Ландау. Если же в точном дисперсионном уравнении сначала рассмотреть случай 0 = п/2 , то, как показал Бернштейн [10], получающиеся решения (моды Бернштейна) не затухают. То есть все функции f ( ~,ш,ш в ) , например диэлектрическая проницаемость, являются не непрерывными функциями параметров, а имеют обозначенную особенность с переходом к пределу [11].
Отметим, что само понятие электростатических волн в магнитоактивной плазме допустимо лишь в случае перехода к пределу N = kc/ш ^ 1 , N — показатель преломления.
Для объяснения парадокса Бернштейна–Ландау было выдвинуто довольно много идей. Например, о необходимости учета релятивистских поправок или учета связи между продольной и поперечной компонентами поля (то есть отказа от приближения электростатического поля). Сагдеев и Шапиро [12] предположили, что за счет перекрытия резонансов, которые расположены на частотах, кратных ларморовской, при переходе B о ^ 0 становятся существенными нелинейные эффекты. В их статье также исследовался дополнительный механизм затухания, связанный с ускорением захваченных частиц вдоль фронта волны. Последний эффект рассматривался и в статьях [13, 14]. Авторы, в частности, вычислили сдвиг частоты волны за счет нелинейного взаимодействия волны с резонансными частицами.
Наиболее полное исследование парадокса Бернштейна–Ландау в рамках линейной теории провели Baldwin [15], а затем Sukhorukov и Stubbe [11]. В работе [15] показано, что затухание Ландау получается в пределе слабого внешнего магнитного поля в результате суперпозиции мод Бернштейна. Поскольку частоты мод Бернштейна кратны ларморовской, то при переходе к случаю слабого магнитного поля возникает бесконечное число мод Бернштейна с близкими частотами (ведь ш в ^ 0 ). Оказывается, их суперпозиция эффективно приводит к одной результирующей моде с правильным законом дисперсии и декрементом затухания Ландау. Также оказалось, что затухание наблюдается лишь в первом гиропериоде, затем магнитное поле частично восстанавливает амплитуду волны (за счет вращения частиц), причем получающиеся всплески электрического поля происходят каждый гиропериод. Таким образом, поведение волны становится квазиперио-дическим, с периодом Т в = 2п/ш в .
Из всего вышесказанного следует, что как нелинейные эффекты, так и наличие магнитного поля могут остановить затухание Ландау. Поэтому особый интерес представляет случай, когда оба эффекта присутствуют одновременно. На самом деле, присутствие внешнего магнитного поля может предотвратить ослабление затухания Ландау из-за того, что у электронов, вращающихся в магнитном поле, не будет времени для взаимодействия с волной, приводящего к ее усилению. Если оба времени, характеризующие вращение электрона в магнитном поле и осцилляции в потенциальной яме волны, одного порядка, то результаты такого взаимодействия труднопредсказуемы в рамках аналитической теории.
Целью данной работы является исследование затухания Ландау плазменных волн в магнитоактивной плазме путем численного решения уравнения Власова. В последующих разделах будет изложена методика моделирования, полученные результаты и заключение.
II. Описание численной схемы
Распространение электростатической волны во внешнем поле B o ||z описывается следующей системой уравнений:
∂f ∂t
F
—e ( Е + c[v,-Bо] );
/ +^
div Е = 4ne I no — fdv
-∞ где f — функция распределения электронов, e — элементарный заряд, no — невозмущенная плотность. -
В таком случае для колебаний в плоскости, перпендикулярной B о, задача сводится к одномерной в конфигурационном пространстве и двумерной в пространстве скоростей (что учитывает ларморовское вращение частиц), так как по z , y и v z уравнения можно проинтегрировать (предполагается, конечно, что начальное возмущение плотности зависит только от x ). В случае неза-магниченной плазмы уравнение Власова становится одномерным и в пространстве скоростей. Схема интегрирования, за исключением очевидных преобразований, не изменится при переходе от одномерного случая к двумерному, поэтому более подробно рассмотрим случай 1D–1D
58 Физика, электроника, нанотехнологии ТРУДЫ МФТИ. — 2011. — Том 3, № 2 (то есть без магнитного поля — одномерный в конфигурационном пространстве и пространстве скоростей). Величины были обезразмерены следующим образом: t → tω p , x → xk , n → n/n 0 , E ^ E/(4nen o /к ) , где k — волновое число начального возмущения электронной плотности.
В безразмерных переменных уравнение Власова (1) запишется в виде
∂f ∂f
dt + vx dx
-
Ex f =0.
В качестве пространственной области, занимаемой плазмой, выбран отрезок длиной L — 2п . Размеры области по скорости L v — [- п,п ] . Задача решалась с периодическими граничными условиями в пространстве. Начальное возмущение функции распределения имеет вид 5f in — A cos( x ) /m ( v ) , где / m (v) — максвелловское распределение электронов по скоростям. Интегрирование уравнения Власова (2) осуществлялось посредством схемы расщепления [16, 17]. Схематически она изображена на рис. 6.
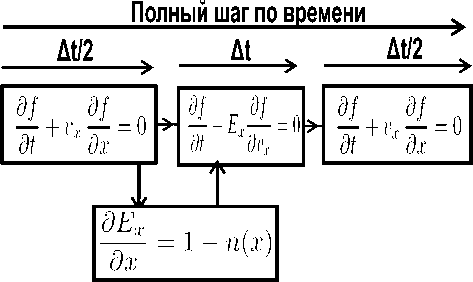
Рис. 6. Схема интегрирования уравнения Власова
Основная идея метода заключается в том, что на каждом шаге по времени уравнение (2) заменяется на два уравнения переноса — перенос в конфигурационном пространстве и перенос в пространстве скоростей:
∂f ∂f
d" + V x dx = 0 ,
∂f ∂t
-
∂f
-Ex — 0.
∂v x
Электрическое поле вычислялось интегрированием уравнения
^Ex — 1 - n(x,t); n(x,t) — j f (x,Vx,t)dvx.
Отметим, что здесь n ( x,t ) рассчитывается по функции распределения, полученной после интегрирования уравнения (3). Сами же уравнения переноса интегрировались с помощью метода баланса потоков (flux balance method) [17]. Функция f ( t + t ) получается при интегрировании любого из уравнений переноса путем подсчета потери и прихода «вещества» в данную ячейку фазового пространства ( x i ,V j ) :
/(t + t,i,j) — f (t,i,j) + Sf (t,i T 1,j) - Sf (t,i,j);
S/(t,i,j) = |vj I - (f (t,i,j) ± |[f (t,i + 1,j) - f (t,i - 1,j)] f1 - |vj I-) } . x4 x
Верхний знак берется для V j > 0 , нижний — в противном случае. Эти формулы очевидным образом видоизменяются для интегрирования второго уравнения переноса.
Во внешнем магнитном поле обезразмеренное уравнение Власова запишется в виде
∂f ∂t
∂f
+ v x
∂x
-
∂f ∂f
(Ex + VyWB)---+ Vx шв^— — 0.
∂v x ∂v y
Схема интегрирования остается, по сути, той же: сначала учитываются пространственные переносы, затем переносы в пространстве скоростей и, наконец, снова переносы в конфигурационном
ТРУДЫ МФТИ. — 2011. — Том 3, № 2 Физика, электроника, нанотехнологии 59 пространстве. Как было сказано выше, в данной программе для определения электрического поля использовалось уравнение Пуассона.
III. Результаты моделирования
Работоспособность и адекватность результатов численного кода была проверена на сравнении результатов моделирования распространения ленгмюровской волны в отсутствие магнитного поля как для режима Ландау, так и для режима О’Нейла с аналитическими оценками, полученными ранее.
Для исследования обоих режимов начальная температура электронов выбрана как T = 0,1 , что соответствует слабому затуханию (в смысле, y l ^ Ш Р (см. табл. 1)). В качестве варьируемого параметра выбрана амплитуда начального возмущения, поскольку именно она определяет соотношение γ L τ b при заданном γ L , то есть характеризует степень нелинейности затухания. Основным критерием адекватности выполненных вычислений является сохранение энергии всей системы.
На рис. 7, 8, 9 изображены зависимости энергии электрического поля от времени для разных амплитуд волны. Для всех представленных в данной работе данных закон сохранения энергии выполняется с точностью до SW totai = 8 х 10 - 5 (максимальное значение для A = 0,1 ). Таким образом, точность результатов численной схемы в этом смысле довольно высока.
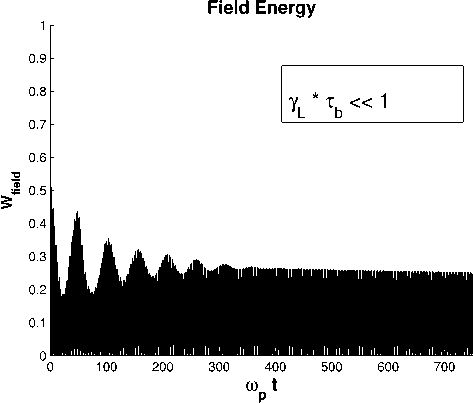
Рис. 7. Эволюция волны в режиме О’Нейла Рис. 8. Эволюция волны в режиме О’Нейла (A = 0 .1) (A = 0 .01)
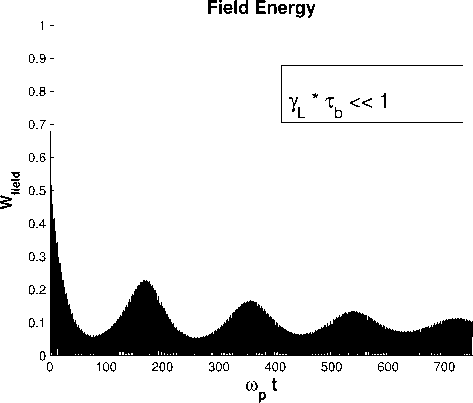
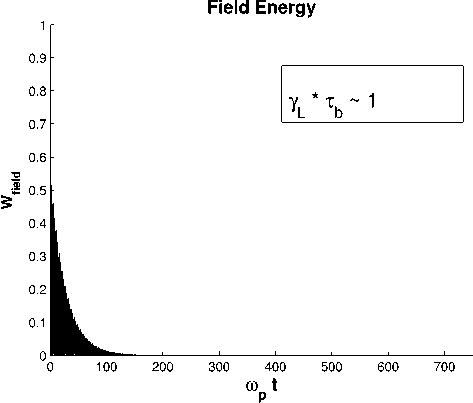
Рис. 9. Эволюция волны в режиме Ландау ( A = 0 .001)
Для каждого значения параметра A вычислены теоретические значения декрементов затухания и экспериментальные. Все значения декрементов затухания представлены в табл. 1. Как
60 Физика, электроника, нанотехнологии ТРУДЫ МФТИ. — 2011. — Том 3, № 2 видно из этой таблицы, разница между теоретическими и полученными при моделировании декрементами затухания (табл. 1) составляет не более 12% , что позволяет сделать вывод о хорошей точности численного моделирования эволюции ленгмюровской волны и адекватности выбранного метода. На рис. 7--9 видно, что быстрые осцилляции происходят на плазменной частоте, то есть соответствуют самим ленгмюровским колебаниям, в то время как медленные осцилляции (модуляция амплитуды) происходят за счет нелинейных эффектов, связанных с влиянием захваченных волной частиц.
Таблица 1
|
Амплитуда возмущения, A |
γ L th eory |
γ L exp |
δW total |
|
1•10 - 1 |
0,0297 |
0,0288 |
6,0 • 10 - 5 |
|
1 •10 - 2 |
0,0272 |
2,5 • 10 - 7 |
|
|
1•10 - 3 |
0,0272 |
3,0 • 10 - 10 |
Как видно из рис. 7–9, результаты моделирования в нелинейном режиме полностью соответствуют изложенной выше теории О’Нейла, а именно: на рис. 7 и рис. 8 изображен случай Yl т ь ^ 1 , эволюция амплитуды волны происходит в режиме О’Нейла, то есть волна не затухает полностью, переходя в стационарный режим, как и должно быть согласно теоретическим исследованиям. На рис. 9 иллюстрируется затухание в режиме Ландау — волна полностью затухает до того, как нелинейные эффекты начнут сказываться на эволюции волны.
Теперь перейдем к результатам моделирования затухания Ландау в плазме с магнитным полем. Очевидно, что к параметру γ L τ b , разделявшему режимы О’Нейла и Ландау в случае B 0 = 0 , добавится также параметр κ = ω B /ω A . Этот параметр характеризует влияние магнитного поля на эволюцию колебаний в нелинейном режиме. В соответствии со сказанным выше представляется разумным для большей наглядности привести результаты по режимам О’Нейла и Ландау последовательно, чтобы увидеть, как именно влияет изменение параметра κ на колебания в каждом из этих режимов.
Сначала рассмотрим режим О’Нейла. Амплитуда начального возмущения A = 0 , 1 и соответственно y l т ь ^ 1 , то есть нелинейные эффекты, связанные с динамикой захваченных частиц, в данном случае чрезвычайно сильны, и без магнитного поля волна не затухает (рис. 7). Слабое магнитное поле (то есть малое ω B как по сравнению с ω p , так и по параметру κ ) приводит к слабому уменьшению амплитуды модуляции энергии и волна не затухает (ср. рис. 7 и рис. 10). Практически невозможно численно исследовать эволюцию колебаний плазмы на временах порядка нескольких гиропериодов при постепенном уменьшении магнитного поля, поэтому вопрос о конечной стадии эволюции волны остается открытым до сих пор.
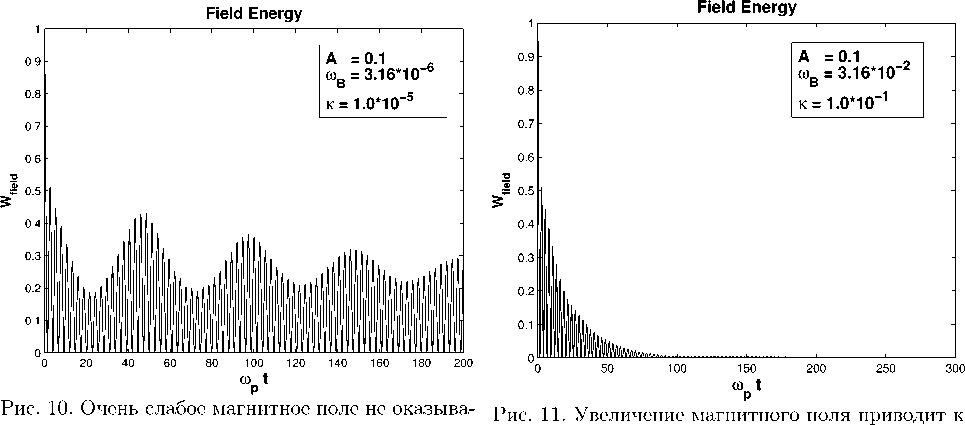
ет почти никакого влияния на эволюцию волны полному затуханию
Последующее увеличение ωB (магнитного поля) при сохранении κ < 1 приводит к интересному эффекту: волна полностью затухает (см. рис. 11)! Это можно объяснить тем, что магнитное поле выводит захваченные частицы из резонансной области, предотвращая, таким образом, передачу энергии ими обратно электрическому полю. Таким образом, эффекты от магнитного поля, конкурируя с нелинейными эффектами, оказывают воздействие прямо противоположное тому, что происходит в линейном режиме.
Дальнейшее увеличение магнитного поля до значения κ > 1 , наоборот, предотвращает всякое затухание поля (рис. 12) и приводит к генерации бернштейновских мод [10]. Очевидно, что между режимом затухания и режимом генерации бернштейновских мод должен существовать некий промежуточный режим, но нам не удалось воспроизвести его в нашем моделировании. Основные параметры и результаты занесены в табл. 2.
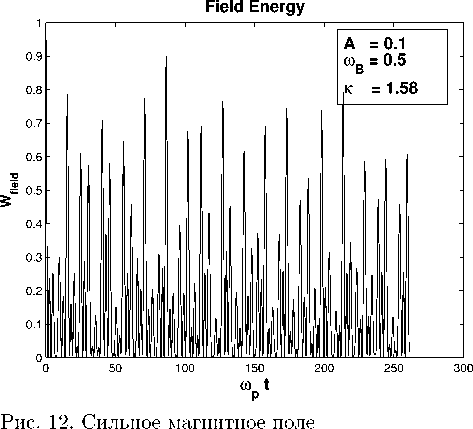
Таблица 2
|
Амплитуда начального возмущения, A |
ω B |
κ = ω B /ω A |
Асимптотическое поведение волны |
δW total |
|
1 · 10 - 1 |
0 |
0 |
Не затухает |
6 · 10 - 5 |
|
3,16 · 10 - 6 |
1 · 10 - 5 |
Не затухает |
7 · 10 - 6 |
|
|
3,16 · 10 - 2 |
0.1 |
Затухает |
4 · 10 - 6 |
|
|
0.5 |
1.58 |
Не затухает |
8 · 10 - 5 |
Перейдем теперь к изучению влияния магнитного поля на затухание волны в режиме Ландау. Амплитуда начального возмущения A = 0,001 , γ L τ b ∼ 1 , и волна полностью затухает при B 0 = 0 , как видно из рис. 9. На графиках, представленных на рис. 13 и 14, приведены результаты моделирования для κ = 3,16 и κ = 9,49 . Для параметра κ = 3,16 (рис. 13) гиропериод T B сравним со временем, за которое волна раньше затухала, и сейчас до времени t = T B затухание происходит совершенно так же, как и в плазме без магнитного поля. Однако в момент времени T B амплитуда волны, в полном соответствии с теоретическими предсказаниями, скачкообразно возрастает [11]. Следующие скачки амплитуды приходятся на времена, кратные гиропериоду. Таким образом, появление магнитного поля действительно предотвращает затухание волны, которое наблюдается лишь в первом гиропериоде.
Последующее увеличение κ еще более сильно ослабляет затухание, и амплитуда осцилляций достигает уже 80% от первоначальной (рис. 14). Заметим, что амплитуда осцилляций возрастает с ростом κ . В данном режиме уже можно говорить об эволюции берштейновских мод, а не об эволюции ленгмюровских волн. Отметим, что случай κ < 1 не рассматривался, так как это условие означало бы, что гиропериод больше τ b , а волна затухает задолго до этого времени. В табл. 3 представлены основные параметры и результаты.
Таблица 3
|
Амплитуда начального возмущения, A |
ω B |
κ = ω B /ω A |
T B = 2π/ω B |
Асимптотическое поведение волны |
δW total |
|
1 • 10 - 3 |
0 |
0 |
го |
Затухает |
3 • 10 - 10 |
|
0,1 |
3,16 |
62.83 |
Не затухает |
6 • 10 -7 |
|
|
0,3 |
9.49 |
20.94 |
Не затухает |
2 • 10 - 6 |
Заключение. Работа посвящена изучению нелинейного режима затухания Ландау продольных (ленгмюровских) колебаний в плазме, распространяющихся перпендикулярно постоянному магнитному полю. Наиболее полное исследование задачи возможно лишь с помощью численного решения уравнения Власова, описывающего бесстолкновительную плазму. В качестве численной схемы была выбрана, вероятно, одна из самых распространенных схем интегрирования кинетического уравнения — схема расщепления. Основное ее достоинство заключается в высокой скорости вычислений и хорошей точности полученных результатов ( δW total < 10 - 4 ).
Показано, что эволюция волны носит бифуркационный характер, то есть при изменении значения некоторого управляющего параметра (например κ = ω B /ω A ) затухание волны прекращается. В частности, если в отсутствие магнитного поля γ L τ b > 1 (режим Ландау) волна затухала, то по мере увеличения магнитного поля затухание волны предотвращается доминирующим воздействием магнитного поля (рис. 13). В режиме О’Нейла ( y l т ь ^ 1 ) влияние магнитного поля совершенно иное. Слабое магнитное поле (в смысле малости параметра κ и ω B ) практически не меняет амплитуду осцилляций огибающей электрической энергии. Затем, при переходе через пороговое значение амплитуды магнитного поля, первоначально не затухающая волна затухает на временах порядка гиропериода (рис. 11). Дальнейший рост амплитуды магнитного поля опять останавливает затухание волны и приводит к генерации бернштейновских мод (рис. 12). К сожалению, нам не удалось обнаружить пороговое значение магнитного поля в обоих случаях, и, как следствие, воспроизвести эволюцию волны при критическом значении κ . Результаты моделирования согласуются, таким образом, с теоретическими и численными исследованиями, проведенными ранее [10, 11, 18].
Список литературы Эволюция электростатической волны, распространяющейся перпендикулярно однородному магнитному полю в плазме
- Ландау Л.Д. О колебаниях электронной плазмы//Л.Д. Ландау. Собрание трудов. -1946. -Т. 2. -С. 7-26.
- ONeil T. Collisionless damping of nonlinear plasma oscillations//Phys. Fluids. -1965. -V. 8, N 21. -P. 2255-2262.
- Isichenko M.B. Nonlinear Landau damping in collisionless plasma and inviscid fluid//Phys. Rev. Lett. -1997. -V. 78, N 12. -P. 2369-2372.
- Brodin G. Nonlinear Landau damping//Phys. Rev. Lett. -1997. -V. 78, N 7. -P. 1263-1266.
- Bernstein I.B., Greene J.M., Kruskal M.D. Exact nonlinear plasma oscillations//Phys. Rev. -1957. -V. 108, N 3. -P. 546-550.
- Lancelotti C., Dorning J.J. Critical initial states in collisionless plasma//Phys. Rev. Lett. -1998. -V. 81, N 23. -P. 5137-5140.
- Danielson J.R., Anderegg F., Driscoll C.F. Measurement of Landau damping and the evolution to a BGK equilibrium//Phys. Rev. Lett. -2004. -V. 92, N 24. -P. 245003-1-245003-4.
- Carbone V., De Marco R., Valentini F., Veltri P. The failure of Vlasov approximation//EPL. -2007. -V. 78. -P. 65001-p1-65001-p6.
- Арцимович Л.А., Сагдеев Р.З. Физика плазмы для физиков. -М.: Атомиздат, 1979.
- Bernstein I.B. Waves in a plasma in a magnetic field//Phys. Rev. -1958. -V. 109, N 1. -P. 10-21.
- Sukhorukov A.I., Stubbe P. On the Bernstein-Landau paradox//Phys. Plasmas. -1997. -V. 4, N 7. -P. 2497-2507.
- Сагдеев Р.З., Шапиро В.Д. Влияние поперечного магнитного поля на затухание Ландау//Письма в ЖЭТФ. -1973. -Т. 17, В. 7. -С. 389-393.
- Krasovsky V.L., Sagdeev R.Z., Zelenyi L.M. Plasma wave frequency shift in a weak transverse magnetic field due to trapped particle acceleration//Phys. Lett. A. -2006. -N 355. -P. 129-133.
- Krasovsky V.L., Sagdeev R.Z., Zelenyi L.M. Wave-trapped particle interaction in a weak transverse magnetic field//Phys. Lett. A. -2006. -N 360. -P. 713-716
- Baldwin D.E., Rowlands G. Plasma oscillations perpendicular to a weak magnetic field//Phys. Fluids. -1966. -V. 9, N 12. -P. 2444-2453.
- Cheng C.Z., Knorr G. The integration of the Vlasov equation in configuration space//J. Comput. Phys. -1976. -V. 22. -P. 330-351.
- Fijalkow E. A numerical solution to the Vlasov equation//Comp. Phys. Comm. -1999. -V. 116. -P. 319-328.
- Valentini F., Veltri P., Mangeney A. Magnetic-field effects on nonlinear electrostatic-wave Landau damping//Phys. Rev. E. -2005. -V. 71. -P. 016402-1-016402-8.


