Эволюция кутрита и контракция алгебры Ли su (3)

Под описанием физической системы понимается построение ее математического образа, выраженного через наблюдаемые системы. В классической физике наблюдаемые системы –это вещественные бесконечно дифференцируемые функции координат и импульсов, образующие коммутативную алгебру вещественных гладких функций на фазовом пространстве [1]. В квантовой физике наблюдаемой сопоставляется линейный оператор, а сама система описывается, вообще говоря, некоммутативной алгеброй операторов в линейном пространстве [1, 2].

Для связи линейных операторов с экспериментальными данными, которые являются вещественными числами, служит матрица плотности р- Tr р = 1 , описывающая состояние квантовомеханической системы. Среднее значение наблюдаемой A физической системы, находящейся в состоянии ρ , дается выражением < A >  = Tr ( Ар ) .

Динамика замкнутой квантовой системы определяется унитарным оператором эволюции, поэтому ее алгебра наблюдаемых не изменяется в процессе эволюции системы. Другая картина имеет место для открытых квантовых систем, взаимодействующих с окружающей средой. Эволюция таких систем уже не описывается в терминах унитарной гамильтоновой динамики и, следовательно, алгебра наблюдаемых может изменяться в ходе ее эволюции. Изменение во времени матрицы плотности в общем случае описывается преобразованием Крауса р (t ) = Л( t) р (0) = ^ Bk (t) р (0) B+( t),

Е B + ( t ) B k ( t ) = 1 .             (1)

k

При малом времени взаимодействия с окружением можно пренебречь эффектами памяти (марковское приближение) и тогда эволюцию системы можно описать уравнением Линдблада [3–5]

Эволюция алгебры динамических переменных A ( t ) тогда имеет вид

A ( t ) = Л J ( A )=e L t A (0) ,         (4)

а изменение во времени коммутационных соотношений дается формулой

[ A i -A ] t = (Л J ) " 1 [Л J ( A i ) , Л J ( A i )] = C k ( t ) A k ,

(5) которая представляет собой типичное преобразование коммутационных соотношений между генераторами при контракции групп (алгебр) Ли [6–8]. Таким образом, имеется естественная связь между диссипативными процессами в открытых квантовых системах и контракциями групп (алгебр) Ли, которая анализируется в трудах [9–11]. В работах [12, 13] подробно изучена связь квантовых каналов кубита с контракциями алгебры su (2) .

В данной статье мы продолжаем изучать Ли-алгебраический подход к исследованию открытых квантовых систем теперь на примере кутрита – трехуровневой системы с алгеброй симметрии su (3) . Трехуровневые системы появляются во многих областях. Например, частица спина 1 в магнитном поле, нейтринные осцилляции, три выделенных уровня в атоме, лазерной спектроскопии, квантовой электронике, КХД, в квантовых моделях фотосинтеза [14– 17].

^р=- ~ H ,^р ]⁺

1. Поперечная релаксация кутрита

+ E Y k V v _k^V i + - 2 { V k ⁺ V k ,р }) •

Матрица плотности ρ кутрита может быть представлена в виде линейной комбинации генераторов алгебры Ли и (3)

Первое слагаемое в правой части уравнения отвечает унитарной части динамики системы, генерируемой гамильтонианом H , который в общем случае включает гамильтониан системы, а также содержит дополнительные слагаемые, относящиеся к взаимодействию с окружением. Второе слагаемое описывает диссипативную часть динамики. Операторы V k обычно называют операторами Линдблада, а неотрицательные γ k играют роль скоростей релаксации для различных видов затухания открытой квантовой системы.

Диссипативные процессы в открытых квантовых системах могут приводить к обнулению некоторых коммутаторов алгебры наблюдаемых, что интерпретируется как частичная потеря системой квантовых свойств, т.е. частичному переходу от квантового поведения к классическому. Появляющиеся при этом коммутирующие наборы наблюдаемых интерпретируются как классические переменные, возникающие в результате диссипации.

В картине Гейзенберга для наблюдаемых A уравнение Линдблада имеет вид

где

⃗ a

A = ~ H-A ]⁺

+E Yk (V ⁺ AV k - 2 { V k ⁺ V k .A

1 I ³

2 I

р =11+1 a р 3    2

a 1 + ia 2 а 4 + га 5

a 4

a 6

-

-

-

ia 5 ia ₇ 2

⁽ a 1 ^- a 2 ^- • • • ^- a 8 ) ^-

■ А =

a 1

-

-

ia 2

a 6 + га 7

,

вектор Блоха, λ

( А 1 • • •, А 8 ) - матрицы Гелл-Манна вида

^{А 1}=(

А 4 ⁼

А 6 =

^А 3 = ^

) 40

-i

0 0

,

) 40

-

,

)^{- А 7}=(

г

-

,

- 1

)^{-А 8} =;1з(

- 2

.

В качестве базисных состояний кутрита мы используем обозначения

I 1 ^ — ( 0 ) , ^{1 2} ^ — ( 0 ) , ^{1 3} ^ = ( 1 ) ' (8)

слагаемых. Например, в случае декогеренции кут-рита, приводящей к обнулению (с одинаковой скоростью для вещественной и мнимой частей) недиагональных элементов матрицы плотности, ее можно получить как решение уравнения (2) с операторами Линдблада

Неунитарная эволюция кутрита, приводящая к его декогерентности [9–12], описывается преобразованием Крауса (1) c набором диагональных матриц вида

V ^1—(

-

). V ^2—(

— 1 0

,

/ - 10 0

в 1 = Vp T I , B 2 = VP 2   0 10

V 0 0 1

V 3 —

-

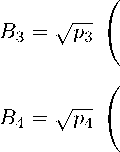
- 1 0

,

и гамильтонианом

H — diag ( E 1 , E 2 ,E 3 ) ,

1 0 0

01 0

0 0 - 1

где E _i обозначает энергию i -го уровня. Действительно, диагональные элементы матрицы плотности стационарны P ii — 0 , i — 1 , 2 , 3 , а недиагональные элементы подчиняются простым уравнениям

где

/5 12 ^{— —а} 12 P 12 ,  / 5 13 ^{— —а} 13 P 13 ,

Р 1 — 4 ⁽¹ + ^e 1 ^e 3 + ^e 2 ^e 3 + ^e 1 ^e 2 ) ,

Р 2 — |(1 - e 1 e 3 + e 2 e 3 - e 1 e 2 ) ,

Р 3 — 4(1 — e 1 e 3 — e 2 e 3 + e 1 e 2 ) ,

Р 4 ^— 4 ^{(1 + e} 1 ^e 3 ^{— e} 2 ^e 3 ^{— e} 1 ^e 2 ) ■

Оно приводит к матрице плотности кутрита

P — ^E k PE + —

k

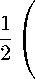
2 ⁺ a 3 ^{+ —} a 8 33

^e 1 ^e 3 ⁽ a 1 ⁺ ia 2 )

e 1 e ₂ ( a 4 + ia 5 )

e 1 e 3 ( a 1 - ia 2 ) 3 ^— a 3 ⁺ 4 13 a 8 ^e 2 ^e 3 ⁽ a 6 ^{+ ia} 7 )

e 1 e 2 ( a 4 — ia 5 ) ^e 2 ^e 3 ⁽ a 6 ^{— ia} 7 )

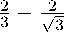
Эта же матрица плотности получается преобразованием генераторов

λ i → T ij λ j ,                 (12)

где T ij - диагональная матрица с элементами T 11 — T 22 ^{— e} 1 ^e 3 , T 44 ^— T 55 ^{— e} 1 ^e 2 , T 66 ^— T 77 ^{— e} 2 ^e 3 , T ₃₃ — T 88 — 1 , которое имеет вид контракции Виг-нера-Иненю [6, 8, 18]. При переходе к новому базису структурные константы в алгебре Ли преобразуются по правилу

C kj ( t ) — T - ¹ T im T ₃n C^a_{m n} ■ (13)

В общем случае эволюция кутрита описывается уравнением (2), в котором сумма по k берется от единицы до восьми. В частных случаях диссипации кутрита можно обойтись меньшим числом

P 23 — —а 23 P 23               (16)

с параметрами а 12 — 2(Y1 + Y2) + iw 12, а 13 — 2(y 1 + Y3) + iw 13, а 23 — 2( Y 2 + Y 3) + iw 23,          (17)

где действительная часть α _ij есть скорость затухания интерференции между уровнями i и j , которая описывается элементом ρ ij матрицы плотности кут-рита, а мнимая часть есть разность энергий w ij — ( E j — E i ) / ~ . Решения уравнений имеют вид

P 12 ( t ) — e - ^{а 12} t р 12 (0) , р 13 ( t ) — e - ^{a 13} t p 13 (0) ,

P 23 ( t ) —e - ^{a 23} t P 23 (0) ■             (18)

Обозначая e 1 e ₃ — e - ^{a 12} t , e 1 e ₂ — e - ^{a 13} t , e ₂ e ₃ — e - ^{a 23} t , получаем для матрицы плотности p ( t ) выражение (11).

Что касается эволюции наблюдаемых X i ( t ) (одинаковой для их вещественных и мнимых частей), то из уравнения (3) имеем

^X 3 , 8 ^{— 0} , ^X 1 , 2 ^{— —а} 12 ^X 1 , 2 , ^X 4 , 5 ^{— —а} 13 ^X 4 , 5 ,

^X 6 , 7 ^{— —а} 23 ^X 6 , 7 ■                ⁽¹⁹⁾

Решения этих уравнений имеют вид

^X 3 , 8 ⁽ t ) ^{— X} 3 , 8 , ^X 1 , 2 ⁽ t ) ^{— e а 12} t ^X 1 , 2 ,

X 4 , 5 ( t ) — e - ^{a 13} t X 4 , 5 , X 6 , 7 ( t ) — e - ^{a 23} t X 6 , 7 (20)

и могут быть представлены в виде (12) как преобразования контракций. Преобразованные генераторы образуют алгебру su (3 , e ) с коммутационными соотношениями

[ ^X 1 ,^X 2 ] t ^{— 2 ie} 1 ^e 3 ^X 3 , [ ^X 1 , ^X 3 ] t ^{— — 2 iX} 2 ,

[ ^X 1 , ^X 4 ^] t ^— i^e 1 ^X 7 ,   ^{[ X} 1 , ^X 5 ] t ^{— —}i^e 1 ^X 6 ,

^{[ X} 1 , ^X 6 ^] t ^{— ie} 3 ^X 5 , ^{[ X} 1 , ^X 7 ^] t ^{— —ie} 3 ^X 4 ,

[ A i , A 8 ] t = 0 , [ A 2 , A 3 ] t = 2 iA 1 ,

^{[ A} 2 , ^A 4 ^] t = ^ie 1 ^e 3 ^A 6 , ^{[ A} 2 , ^A 5 ] t = ^ie 1 ^e 3 ^A 7 ,

^{[ A} 2 ^,A 6 ^] t = ^-ie 3 ^A 4 , ^{[ A} 2 ^,A 7 ^] t = ^-ie 3 ^A 5 ,

^{[ A} 2 ^,A 8 ^] t = ⁰ ,   ^{[ A} 3 ^,A 4 ^] t = ^iA 5 ,

[ A 3 , A 5 ] t = -iA 4 , [ A 3 , A 6 ] t = -iA 7 ,

^{[ A} 3 ^,A 7 ^] t = ^iA 6 ,   ^{[ A} 3 ^,A 8 ^] t = ⁰ ,

^{[ A} 7 , ^A 8 ^] t = i V^{3 A} 6 , ^{[ A} 4 , ^A 6 ^] t = ^-ie 2 ^A 2 , [ A 4 , A 7 ] t = ie 2 A 1 , [ A 4 , A 8 ] t = —i Vs A 5 , ^{[ A} 5 ^,A 6 ^] t = ^—ie 2 ^A 1 , ^{[ A} 5 ^,A 7 ^] t = ^ie 2 ^A 2 , [ A 5 , A 8 ] t = i VS A 4 , [ A 6 , A 8 ] t = —i V3 A 7 , ^{[ A} 4 ,^A 5 ] t = i^e 1 ^e 2 ( ^A 3 + V s ^A 8^ , ^{[ A} 6 ,^A 7 ^] t = i^e 2 ^e 3 ( V s ^A 8 — ^A 3 ) .

При e ₃ = 1 получаем контракции Кэли-Клейна [8]. Контракции алгебры Ли su (3 , e ) при предельных переходах t ^ ж ( e i ^ 0 ) подробно разобраны в работе [18]. Таким образом, мы показали, что эволюция кутрита при наличии поперечной релаксации приводит к диагональной контракции ее алгебры симметрии su (3) .

2. Поперечная и продольная релаксации кутрита

К рассмотренной поперечной релаксации кут-рита можно добавить продольную с переходами между всеми уровнями. При наличии продольной релаксации динамика кутрита затронет также и диагональные элементы его матрицы плотности. Обозначим γ ij вероятность перехода с j -го уровня на i -й (рис. 1). Тогда в уравнении Линдблада к операторам (14) добавятся операторы V ij = ^|i V j I ⁽ i = j )

E 3

E 2

E 1

| 2 )

V 13 = 1 1 V 3 1 = ^ 0	0 0 0	100 ,
V 31 = 1 3 X1 1 = ^ 0	0 0 0	00 ,
0 V 23 = 1 2 )( 3 1 =    0 0	0 0 0	0 )■
0 V 32 = 1 3 )( 2 1 =    0 0	0 0 1	:)■	(22)

и уравнение (2) в этом случае будет иметь вид [19]

^p=^— ~ i[" -^p ]⁺

+ £ Y k V k P^V_k⁺ — ₂ { V k ⁺ V k ,p} + k =1

+ E Y ij U₃pV i + — 2 { V i + V ij ,p }) .    (23)

i ̸ = j

Выпишем эти уравнения отдельно для диагональных и недиагональных элементов матрицы плотности

P¹ mm     ' ^Y mn P nn

-

^Г m P mm ,

n

^p mn     ^a mn ^p mn , ^m = ⁿ, ^a mn   ^a nm ,

где Г n = 52 m Y mn - общая ширина уровня n , a ij = 2 (Г i + Г j )+2 ( Y i + Y j ) + i^ ij , Re a ij — скорость релаксации недиагональных элементов матрицы плотности ρ _ij . Мнимая часть α _ij для нас не существенна и мы будем ее опускать (или подразумевать, что работаем в представлении взаимодействия). Эволюция недиагональных элементов ρ _mn , как это видно из (25), независима друг от друга. В матричной форме уравнения (24), (25)

Y 12 P 22 + Y 13 P 33 — Г 1 p 11

p( t ) =             ^—a 12 P 21

^-α 13 ρ 31

^-α 12 ρ 12

Y 21 P 11 ⁺ Y 23 P 33 ^{— Г} 2 P 22

^-α 23 ρ 32

-α ₁₃ ρ ₁₃

^-α 23 ρ 23

Y 31 P 11 + Y 23 P 22 — Г 3 P 33

)

Рис. 1. Схема переходов между уровнями кутрита.

Fig. 1. The scheme of transitions between the qutrit levels.

V 12 = 1 1 H 2 1 = 000 , 000

V 21 = 1 2 X1 1 =

Недиагональные элементы удовлетворяют уравнениям

^P* ij       ^a ij ^P ij , i < ^j, ^a ji     ^a ij ,       ⁽²⁷⁾

с решениями

P ij ( t ) = e ^-a i ^j t P ij (0) .              (28)

Решения уравнений (24) для диагональных элементов имеют вид

P 11 ( t ) = C 0 + C x e ^{-a - t} + C 2 e ^{-a +} t ,

Р 22 ( t ) = C з + C 4 e ^{-a - t} + C 5 e ^{-a + +} ,

Р зз ( t ) = C 6 + C 7 e "^ + C 8 e ^{-a +} t ,    (29)

где a^ = 1 B ± 1VB2 - 4D, ±   2     2V          ’

B = Ег i = E Y j , i =1        i ̸ = j

D = Y 21 Y 32 + Y 21 Y 13 + Y 21 Y 23 + Y 12 Y 31 +

⁺ Y 31 Y 32 ⁺ Y 23 Y 31 ⁺ Y 12 Y 13 ⁺ Y 12 Y 23 ⁺ Y 13 Y 32 ^-

^C 3 = ( Y 21 Y 13 ⁺ Y 23 Г 1 ) D 0 ,

^C 0 = ⁽ Y 23 Y 12 ⁺ Y 13 ^r 2 ) D 0 ^-

C 6 = (Г 1 Г 2 — Y 12 Y 21 ) D 0 ,

C 4 = ( Y 21 Y 13 + Y 23 (Г 1 — a — )) D 1 ,

^C 1 = ⁽ Y 23 Y 12 ⁺ Y 13 ^(Г 2 ^{— a} - )) D 1 ^-

^C 7 = ^{(( a} - ^{— Г} 1 ^{)( a} - ^{— Г} 2 ) ^— Y 12 Y 21 ) ^D 1 ^-

^C 5 = ⁽ Y 21 Y 13 ⁺ Y 23 ^(Г 1 ^{— a} + )) D 2 ,

C 2 = ( Y 23 Y 12 + Y 13 (Г 2 — a + )) D 2 ,

^C 8 = ^{(( a} + ^{— Г} 1 ^{)( a} + ^{— Г} 2 ) ^— Y 12 Y 21 ) ^D 2 .   ⁽³⁰⁾

Здесь D _i – константы, зависящие от начальных условий.

Таким образом, эволюция матрицы плотности кутрита при наличии как поперечной, так и продольной релаксации описывается матрицей плотности

/ C 0 + C 1 e ^{-a - t} + C 2 e ^-a + ⁺ Р ( t ) =            e ^{-a 12 +} p 21 (0)

\ e ^{a 13 +} p 31 (0)

e ^{-a 12 +} p 12 (0)

C 3 + C 4 e ^{-a - +} + C 5 e ^{-a + +} e ^{-a 23 +} p 32 (0)

e ^{-a 13 +} P 13 (0)

e " 2 ^{23 +} P 23 (0)

C 6 + C 7 e ^-a - ⁺ + C 8 e ^-a + ⁺

При t → ∞ происходит релаксация диагональных элементов матрицы плотности со скоростями α ± и декогеренция недиагональных элементов со скоростями α ij . В целом система стремится к полностью декогерентному стационарному состоянию

C 0   0

Р ( to ) =    ⁰    C 3

C 6

Выше мы рассмотрели эволюцию матрицы плотности в картине Шредингера. В картине Гейзенберга от времени зависят наблюдаемые, и уравнение Линдблада в этом случае примет вид

A ~ ^-A ]⁺

+

E Y ij fc AV ij — 2 { v + V ij ^,A }) = i ̸ = j

= L^ ( A ) .                   (33)

Генераторы A i ( i = 1 , 2 , 4 , 5 , 6 , 7) алгебры su (3) являются наблюдаемыми для кутрита и собственными векторами оператора L ^♯ . Их динамика описывается уравнениями

^A 1 , 2 = ^—a 12 ^A 1 , 2 ^{- A} 4 , 5 = ^—a 13 ^A 4 , 5 ^-

^A 6 , 7 = ^—a 23 ^A 6 , 7 ^{-                (34)}

с решениями

A 1 , 2 ( t ) = e ^{-a 12 +} A 1 , 2 (0) , A 4 , 5 ( t ) = e ^{-a 13 +} A 4 , 5 (0) , A 6 , r ( t ) = e ^{-a 23 +} A 6 , 7 (0) .             (35)

Для генераторов подалгебры Картана удобно перейти к новому базису e0, e± e0 = I, e ± = a±| 1)(11 + b±l 2)(21 + c±13)(31, a± = ^1 (Y21Y32 + Y31 (Г2 — a±)), b± = ^1 (Y12Y31 + Y32(Г1 — a±)), c± = ^ ((Г1 — a±) (Г2 — a±) — y 12Y21), (36) (A - нормировочный множитель), в котором уравнения Линдблада принимают простой вид e 0 = 0 -    e ± = —a±e ±,         (37)

с решениями e0( t ) = I, e ± (t ) = e-a±+e ± (0).       (38)

Воспользовавшись обратным к (36) преобразованием, которое запишем в виде

1 1X1 1 = f 1 e a + g x e + + h 1 e - ,

| ² )( ² | = f 2 ^e 0 ⁺ g 2 ^e + ⁺ h 2 ^e - ^-

|3)(3 | = f3 e0 + g 3e+ + h 3 e - получим описание динамики наблюдаемых λ3 и λ8

^A 3 ⁽ t ) = ⁽ f 1 ^— f 2 )I^{+ (} g 1 ^— g 2 )^{e a + + e} + ⁽⁰⁾⁺

+ ( h 1 — h 2 ) e ^{a - +} e — (0) ,

^A 8 ⁽ t ) = ⁽ f 1 + f 2 ^{— 2} f 3 ^)I+( g 1 ⁺ g 2 ^{— 2} g 3 )^{e a + + e} + ⁽⁰⁾⁺

+ ( h 1 + h 2 — 2 h 3 )e ^{a - +} e — (0) .       (39)

Таким образом, преобразования контракции наблюдаемых кутрита в новом базисе принимают вид (35), (38), а зависящие от времени коммутационные соотношения этих наблюдаемых даются формулами

[ A 1 ,A 4 ] +	= i e    1	t λ 7 ,	[ A 5 ,A 1 ] +	= i e — A 1 + A 6 ,
[ A 1 ,A 6 ] +	= i e — Л 2	t λ 5 ,	[ A 7 - A 1 ] +	= i e — л 2 + A 4 ,
[ A 6 ,A 4 ] +	= i e — л 3	t λ 2 ,	[ A 2 , A 4 ] +	= i e — A 1 + A 6 ,
[ A 2 ,A 5 ] +	= i e — A 1	t λ 7 ,	[ A 6 ,A 2 ] +	= i e — л 2 + A 4 ,

[ X 7 , X 2 ] t = i e - ^A 2 t X 5 , [ X 6 , X 5 ] t = i e ^{- A} 3 t X 1 ,

[ X 5 , X 7 ] t = ie ^{- A} 3 t X 2 ,   [ X 4 , X 7 ] t = ie ^{- A} 3 t X 1 ,

[ X 1 ,X 2 ] t = 2 i (( f 1 - f 2 )e ^{- 2 a 12} t I+

⁺ ( g 1 ^— g 2 )^{e A} 4 t ^e + ⁺ ( h 1 ^— h 2 )^{e A} 5 t ^e - ) ,

[ X 4 ,X 5 ] t = 2 i (( f 1 — f 3 )e ^{- 2 a 13} t I+

+ ( g 1 — g 3 ) e ^{- A} 6 t e + + ( h 1 — h 3 ) e ^{- A} 7 t e - ) ,

[ X 6 ,X 7 ] t = 2 i (( f 2 — f 3 )6 ^{- 2 a 12} t I+

+ ( g 2 — g 3 ) e ^{- A} 8 t e + + ( h 2 — h 3 ) e ^{- A} 9 t e - ) ,

^{[ X} 1 , ^e ± ^] t = i ⁽ b ± ^— a ± ^{)e a} ± t ^X 2 ,

[ X 2 , e ± ] t = i ( a ± — b ± )e ^a ± t X 1 ,

[ X 4 , e ± ] t = i e ^-a ± t ( c ± — a ± ) X 5 ,

[ X 5 , e ± ] t = i e ^-a ± t ( a ± — c ± ) X 4 ,

^{[ X} 6 , ^e ± ^] t = i ^{e a} ± t ⁽ c ± ^{— b} ± ) ^X 5 ,

^{[ X} 7 , ^e ± ^] t = i ^{e a} ± t ⁽ b ± ^— c ± ) ^X 6 ,

[e + , e - ] t = 0 ,                   (40)

где введены обозначения

Д 1 = ^a 12 ^{+ a} 13 ^{— a} 23 = Y 21 ⁺ Y 31 ⁺ Y 1 >  ⁰ ,

Д 2 = ^a 12 ^{+ a} 23 ^{— a} 13 = Y 12 ⁺ Y 32 ⁺ Y 2 >  ⁰ ,

Д 3 = a 13 + a 23 — a 12 = Y 13 + Y 23 + Y 3 >  0 ,

Д 4 = 2 a 12 — a + , Д 5 = 2 a 12 — a - ,

Д 6 = 2 a 13 — a + , Д 7 = 2 a 13 — a - ,

Д 8 = 2 a 23 — a + , Д 9 = 2 a 23 — a - .     (41)

Параметры Д i , i = 1 , 2 , 3 положительны, а Д k , k = 4 ,..., 9 могут принимать положительные, отрицательные и нулевые значения. Именно они определяют предельное поведение кутрита и коммутационные соотношения его алгебры симметрии в пределе t → ∞ .

При Д _k >  0 , к = 4 ,..., 9 , т.е. 2 a ij > a ± все коммутационные соотношения обращаются в нуль, и алгебра становится абелевой. При Д ₄ , 6 , 8 = 0 , т.е. 2 a ij = a + , i = j , добавляются три ненулевых коммутатора

^{[ X} 1 ,^X 2 ^] ^ = ² i ⁽ g 1 ^— g 2 ^)e + ⁽ t ) ,

[ X 4 , X 5 ] ^ = 2 i ( g 1 — g s )e + ( t ) ,

^{[ X} 6 ,^X 7 ^] ^ = ² i ⁽ g 2 ^— g 3 ^)e + ⁽ t ) .         ⁽⁴²⁾

Если какой-то из параметров Д _k , к = 4 ,..., 9 отрицателен, то появляются сингулярные коммутаторы, что свидетельствует о разрушении кутрита как физической системы.

В обзоре [20] приведен пример, где для двухуровневой системы в оптическом диапазоне скорости поперечной и продольной релаксации относятся, как один к двум, и отмечено, что для подавляющего большинства оптических систем наблюдается существенное превышение скорости дефазировки (поперечной релаксации) над скоростью релаксации энергии (продольной скоростью). В реальных системах это отношение может достигать пяти порядков.

Таким образом, в процессе эволюции трехуровневой квантовой системы с унитарной симметрией SU (3) при наличии взаимодействия с окружающей средой, приводящего к диссипации и декоге-ренции матрицы плотности, происходит обнуление коммутационных соотношений наблюдаемых кутри-та, что математически отвечает контракции алгебры симметрии системы. Физически такое поведение свидетельствует о частичной (или полной) потере кутритом квантовых свойств.

Авторы выражают глубокую благодарность А.А. Карабанову за плодотворные обсуждения.