Эволюция напряжённого состояния и оценка работоспособности узла болтового соединения вязкоупругих композиционных пластин

F =^ F n >  nQ

, где Fтр – сила трения в стыке между пластинами; Fn – нормальная реакция в стыке, Н; μ – коэффициент трения; Q – растягивающее усилие, Н; n – коэффициент запаса.

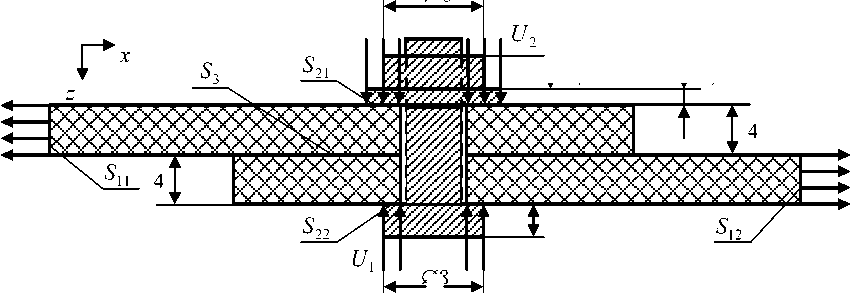
При такой постановке болт в соединении не работает на срез и смятие. Задача рассматривается в трёхмерной постановке. Схема нагружения представлена на рис. 1.

Пластинки из композиционного материала занимают область V. Поверхность нагруженных концов пластинок ^ = S _T u S ₂. Поверхность стыковки пластинок с элементами крепления и приложения перемещений от действия сил затяжки болта S 2 = S 21 u S 22 . Все ненагруженные поверхности обозначим как S 4 . Рассматриваются только композитные пластинки. Запишем постановку задачи в рамках линейной теории вязкоупругости ортотропных материалов:

div(G(x)) = 0 x e v ,                   ,

E(x)=2(Vu(xHVu (x))T) xE V ,                   ,

G ( x, t) = 4 R* • •£ ( x, t) = t

j 4 R (t-t)^^ d s( x, t)

0                           , x e V .

где x – вектор координат точек пластинок; σ – тензор напряжений; ε – тензор деформаций; u – вектор перемещений; t – время; 4R* – тензор интегральных вязкоупругих операторов; 4R(t) – тензор функций релаксации материала пластинок.

Граничные условия:

о (x )• n ( x ) = 0 x g S^

°xx (x) = P Tyx (x) = 0 ,                                      ,

T xz ( x) = 0 x G S1

,,

uz (X) = U2 X G S21 uz (x) = —U 1 ,                         , x G S22

3,5

0,8

p

p

3,5

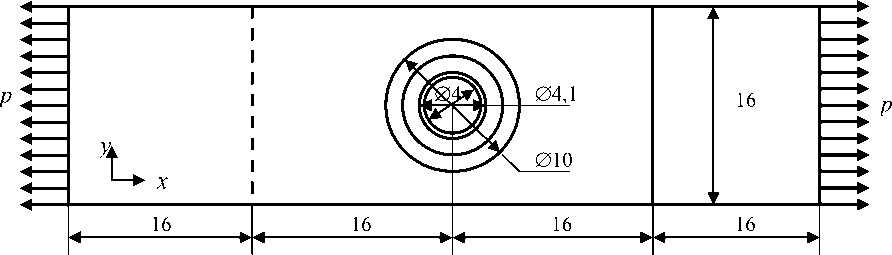
Рис. 1. Схема нагружения болтового соединения: – композиционный материал V ; – материал креплений

Так как площадь поверхности приложения усилий затяжки болта S 2 много меньше площади стыковки пластин, то на этой поверхности можно пренебречь касательными напряжениями τ_xz и τ y _z :

Txz(x) = 0 Tyz (x) = 0 x G S2 ,    ,.

Материал композиционных пластинок представляет собой стеклопластик на основе эпоксидного связующего ЭДТ-10. Для описания компонент тензора функций релаксации 4R(t) данного материала выберем выражение:

/(t) = C(0)+ Ус(rk!)• et ijkl              ijkl              ijkl r=1

.

Коэффициенты C ijkl ^(r) в МПа и γ^(r) в с^–1 приведены в табл. 1.

Таблица 1. Значения коэффициентов функций релаксации

r	γ(r)	(r) С 1111	C 1122 (r) = C 1133 (r)	C 2222 (r) = C 3333 (r)	(r) C 2233	(r) C 2323	C 1313(r) = C 1212(r)
0		6254	3166	20000	15700	14900	1721
1	0,2085 10–1	130,2	-34,48	304,3	-239,9	49,17	140,5
2	0,4555 10–1	101,8	-26,58	239,7	-188,6	38,14	110,3
3	0,8757 10–1	284,2	-74,67	645,1	-505,4	105,6	303,7
4	0,5205 10–1	697,1	-172,5	1625	-1271	251,2	755,0
5	0,6303 10–1	910,5	-217,1	1645	-1175	294,7	916,4

Поставленная задача вязкоупругости содержит несколько независимых интегральных операторов Ry_H , для ее решения используем приближенный метод квазиконстантных операторов [10]. Для оценки погрешности решения задачи определены показатели квазиконстантности [10] всех входящих в неё операторов R yki и установлено, что ^1313 = Хпп =0,116, а значения остальных не превышают 0,057. Следуя [10], верхнюю оценку относительной погрешности решения можно определить как 6%. Метод квазиконстантных операторов позволяет перейти от вязкоупругой задачи к последовательности упругих задач с переменными по времени упругими константами. Решение упругой задачи для каждого момента времени производилось методом конечных элементов при помощью пакета ANSYS. Использованы трёхмерные 8-узловые конечные элементы. Воздействие усилий затяжки болта на стеклопластик учитывается путем задания на соответствующих контактных поверхностях перемещений, имитирующих сближение контактных поверхностей при затяжке. Во времени данные перемещения не изменяются (предполагается, что жесткость пластика в поперечном направлении на много ниже жесткости болта).

что вязкоупругие эффекты могут привести к нарушению работоспособности соединения.

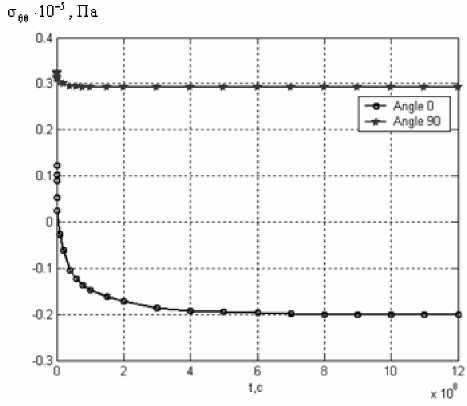
Рис. 2. Графики изменения во времени напряжений о₉₉ на кромке отверстия

ОГ1 Ю'^Па

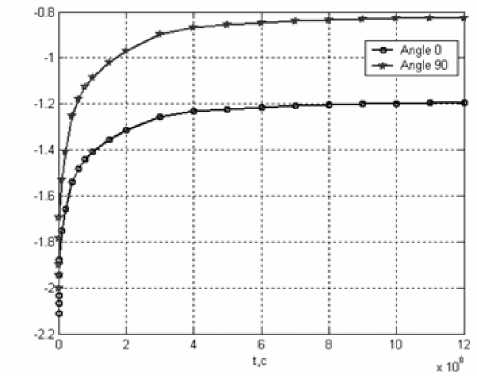
Рис. 3. Графики изменения во времени напряжений o_zz на кромке отверстия

Основной интерес в данной задаче представляет напряжённое состояние возле отверстия под болт, так как оно является концентратором напряжений, а также плоскость стыка композиционных пластинок. Результаты расчёта соединения показали, что при достаточном удалении от отверстия почти все напряжения имеют слабоизменяющийся во времени характер, касательные напряжения малы по сравнению с нормальными. Наибольшими по величине являя-ются напряжения ozz и о99. На рис. 2, 3 приведены графики изменения во времени напряжений ozz и о99 на кромке отверстия для точек, соответствующих углам 0О и 90О в сечении по плоскости стыка в полярной системе координат с центром, совпадающим с центром отверстия.

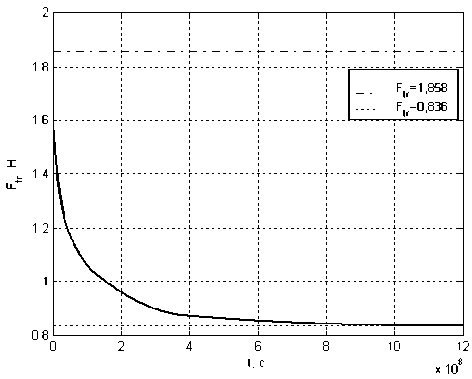
Рис. 4. График изменения во времени силы трения в стыке, Н

Как видно из этих графиков нормальные напряжения o_zz и о₉₉ по абсолютной величине уменьшаются с течением времени. Особенно важно, что уменьшаются по абсолютной величине напряжения o_zz, а, следовательно, уменьшается и интегральная сила трения на поверхности соединения (рис. 4). Относительное изменение силы трения в стыке (рис. 4) составляет 55%. Значение силы к концу рассматриваемого периода времени становится меньше приложенной растягивающей нагрузки F_mp < Q , что может привести к смещению стыка, при этом болт начнёт работать на срез и смятие композиционного материала. Так как изначально болтовое соединение проектировалось с зазором, то можно считать,

Произведем анализ длительной прочности конструкции. В полимерных композитах задолго до разрушения начинают накапливаться микроповреждения, которые могут привести к разрушению конструкции с течением времени даже при относительно низких уровнях напряжений. Подобные явления объясняются теориями длительной прочности, которые служат основой для предсказания долговечности конструкции. Будем считать, что прочность материала пластинок в направлении поперек слоев определяется поведением связующего, а в продольном направлении учет длительной прочности несущественен в силу малости вязкоупругих свойств армирующих стекловолокон.

Следуя теории длительной прочности А.А. Ильюшина [11] при одноосном нагружении величина накопленных повреждений p ( t ) определяется из соотношения

t

Р(t) = J^H (tр -T)d(^11 (T))

0                              ,             (1)

где Su (t) - функция зависимости заданного напряжения от времени до разрушения tp: оц=8ц(tp) при одноосном растяжении вдоль оси 1, которая находится из аппроксимации кривых длительной прочности в виде tр f ^ (tр -т)d(^11 (т)) = 1

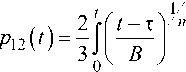
d ( ^ 12 (^т) )

Для рассматриваемой конструкции накопление повреждений в поперечном направлении происходит за счет напряжений обжатия материала пластинок o_zz (данное напряжение непосредственно связано с силой затяжки болта), а сдвиговые повреждения накапливаются за счет касательных напряжений T xz и T yz . Рассмотрим функции повреждаемости в некоторой критической точке конструкции. Под критическими подразумеваются точки, в которых функция повреждаемости имеет наибольшее значение при одинаковом внешнем воздействии. На рис. 5 приведены графики изменения с течением времени функции повреждаемости в поперечном направлении при различных значениях внешней растягивающей нагрузки. Из рис. 5 видно, что при внешней растягивающей силе Q =350 Н значение функции повреждаемости уже при малых временах превышает единичное значение, что означает быстрое разрушение конструкции. При нагрузках меньше 210 Н значение функции повреждаемости не превышает единицу, что означает надежность конструкции на протяжении рассматриваемого периода времени. Приложение растягивающего усилия в диапазоне от 210 до 350 Н дает потерю прочности в различные моменты времени, что подтверждает возможность потери прочности конструкции с течением времени.

Для связующего ЭДТ-10 аппроксимация данных из работы [12] степенным соотношением дает

^11 = ^ п

(tп )=

B

t п

V р 7

где B =2,1185 10³⁸ МПа; n =19,354; t_pⁿ - время до разрушения связующего в поперечном направлении, с.

Так как в поперечном направлении (направлении 2) работает только связующее, то функция повреждаемости в данном направлении с учетом (1) и (2) будет иметь вид

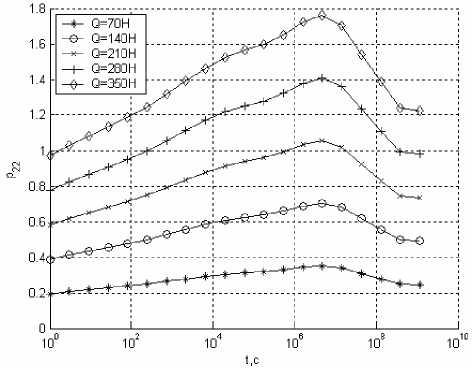
Рис. 5. Изменение функции повреждаемости в поперечном направлении от времени при различных величинах внешней растягивающей силы

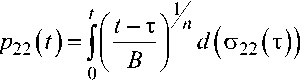
Будем считать, что при чисто объемном деформировании повреждаемость связующего не накапливается, тогда функция повреждаемости от действия сдвиговых напряжений будет следующей

Функции сдвиговой повреждаемости от воздействия напряжений Txz и Tyz даже при нагрузке равной Q=350 Н на протяжении рассматриваемого периода времени остаются много меньше единицы. Следовательно, касательные напряжения создают лишь незначительные повреждения в материале конструкции и поэтому не являются опасными.

Выводы:

• 1.    Установлен и численно исследован эффект эволюции напряженного состояния болтового соединения композитных пластин при постоянном внешнем воздействии. Показана возможность потери работоспособности соединения вследствие релаксации усилия затяжки болта.

• 2.    Оценка длительной прочности позволила определить диапазон значений внешней нагрузки, при которых существует возможность потери прочности соединения.

• 3.    Установлено, что потеря прочности конструкции зависит от напряжений обжатия стеклопластиковых пластин. Накопление сдвиговой повреждаемости незначительно.