Эволюция температурных напряжений в задаче Гадолина о сборке двухслойной упругопластической трубы
Автор: Буренин А.А., Ткачева А.В.
Статья в выпуске: 3, 2020 года.
Бесплатный доступ
Работа направлена на решение задачи теории неустановившихся температурных напряжений, моделирующей операцию сборки двухслойной упругопластической трубы способом горячей посадки (задача Гадолина). Условие пластического течения принимается в форме кусочно-линейного условия максимальных приведенных напряжений (условие Ишлинского - Ивлева) с пределом текучести, параболически зависящим от температуры. Показано, что при решении механической части несвязной задачи теории температурных напряжений расчеты обратимых и необратимых деформаций и напряжений возможно провести численно-аналитически без обращения к приближенным процедурам вычисления и, следовательно, без дискретизации расчетных областей. Рассматривается последовательность возникновения и исчезновения разных областей пластического течения в зависимости от перехода напряженных состояний с одной грани поверхности нагружения (призмы Ивлева) на ее ребро и далее на иную грань при производстве сборки и последующем ее остывании. При разном выборе параметров задачи некоторые из отмеченных пластических областей могут не появляться. Однако других областей пластического течения, изменяя геометрию задачи, свойства материалов сборки и уровень нагрева, получить невозможно. В этом заключается полнота расчетов. Появляются и исчезают только такие пластические области, которые здесь схематически представлены. В отличие от классического случая, заключающегося в равномерном нагреве внешней трубы, в данной статье рассматривается широко используемый на практике случай неравномерного нагрева внешней трубы с внутренней поверхности. При этом рассчитываются, а после учитываются необратимые деформации, зародившиеся в материале трубы до момента посадки. Приводится сравнение распределения остаточных напряжений, полученных при равномерном и не равномерном нагреве внешней трубы.
Упругость, пластичность, температурные напряжения, кусочно-линейное условие пластического течения, сборка с натягом, горячая посадка
Короткий адрес: https://sciup.org/146282001
IDR: 146282001 | УДК: 539.3 | DOI: 10.15593/perm.mech/2020.3.03
Evolution of temperature stresses in the Gadolin problem of assembling a two-layer elastoplastic pipe
The work aims at solving the problem of the theory of unsteady thermal stresses simulating the assembling of the two-layer elastoplastic pipe using the shrink fit (Gadolin problem). The plastic flow condition is taken in the form of a piecewise linear condition of maximum reduced stresses (the Ishlinsky - Ivlev condition) with a parabolic yield point depending on temperature. It is shown that when solving the mechanical part of a disconnected problem of the theory of temperature stresses, the calculations of reversible and irreversible deformations and stresses can be carried out numerically, i.e. analytically without resorting to approximate calculation procedures and, therefore, without discretizing the computational domains. We present a diagram of the emergence and disappearance of plastic flow regions under the assembly conditions and its subsequent cooling. With a different choice of problem parameters, some plastic regions may not appear. However, it is impossible to obtain other areas of plastic flow by changing the geometry of the problem, properties of assembly materials, and the level of heating. This is the adequacy of the calculations. Only those plastic areas that are shown in the diagram appear and disappear. In contrast to the classical case of uniform heating of the outer pipe, this article deals with a widely used case of an uneven heating of the outer pipe from the inner surface. In this case, irreversible deformations are calculated, and then taken into account, which originated in the pipe material before the moment of landing. A comparison of the distribution of residual stresses obtained during the uniform and non-uniform heating of the outer pipe is given. As a result, the interference with the uniform heating exceeds the interference formed with the non-uniform heating of the pipe.
Текст научной статьи Эволюция температурных напряжений в задаче Гадолина о сборке двухслойной упругопластической трубы
ВЕСТНИК ПНИПУ. МЕХАНИКА № 3, 2020PNRPU MECHANICS BULLETIN
Технологическая операция горячей посадки цилиндрических элементов конструкций остается достаточно используемой в ряду технологий сборки с натягом [1]. Еще в самом начале прошлого века А.В. Гадолин предложил в качестве средства повышения прочности стволов артиллерийских орудий использовать их двухслойными и предварительно напряженными, применяя как раз технологию их сборки способом горячей посадки. Такие стволы выдерживали повышенные давления пороховых газов без увеличения их массы, повышая тем самым прицельную дальность стрельбы.
Методическое обеспечение расчетов технологий сборки способом горячей посадки до настоящего времени базируется на теории температурных напряжений в термоупругих телах [1–3]. Необратимое деформирование исключается ввиду существенного повышения в таком случае сложности в расчетах. Действительно, процесс сборки с необходимостью включает в себя как активный процесс нагружения при нагревании, так и процесс разгрузки при остывании сборки. Расчетные области разделяются на области обратимого деформирования и области пластического течения, отделяемые продвигающимися упругопластическими границами, положения которых необходимо указать на каждом временном шаге расчетов. Более того, следует алгоритмически отслеживать моменты и места возникновения и исчезновения областей течения, формировать массивы неизменяющихся необратимых деформаций и исполь- зовать их в расчетах напряжений при разгрузке и остывании, включая возникающие при этом повторные (обратные) пластические течения. Эти обстоятельства затрудняют использование в расчетах наработанных приближенных процедур (конечно-разностных, конечноэлементных), основанных на дискретизации расчетных областей. Только современные вычислительные возможности позволили решить ряд квазистатических задач теории неустановившихся температурных напряжений [4–10], включая задачи, связанные с моделированием операции горячей посадки [11–30].
Известно, что в теории пластичности определенный прогресс был достигнут при использовании кусочнолинейных условий пластического течения [20, 21]. Но применительно к квазистационарным задачам теории неустановившихся температурных напряжений встречаем здесь иную трудность. Д. Бленд, рассматривая задачу о нагреве трубы [22], заметил, что область течения может разделяться на части, где деформирование подчинено разным системам уравнений в зависимости от принадлежности напряжений различным граням и ребрам поверхности текучести. Поэтому число подвижных граничных поверхностей, разделяющих область деформирования на части, увеличивается; повышается и число разных расчетных областей, где приходится интегрировать различные системы уравнений и сопрягать такие расчеты на продвигающихся границах. Тем не менее в [17, 19] при использовании кусочно-линейного условия пластического течения максимальных касательных напряжений [21] (условий Треска – Сен-Вена- на) было показано, что во всех возможных случаях одномерную систему уравнений в задаче посадки трубы на вал даже при зависимости предела текучести от температуры можно записать в перемещениях и проинтегрировать. Следующие на таком пути конечные соотношения позволяют представить напряжения и деформации в каждый рассчитываемый момент времени конкретными зависимостями от распределения температуры по элементам сборки в этот момент времени. Таким способом последовательными шагами расчетов по времени удается избежать необходимости приближенного решения с дискретизацией расчетных областей и отслеживать в каждый такой момент положения граничных поверхностей, включая моменты времени и места в теле их возникновения. Это оказывается справедливым [18] и в случае условия текучести максимальных приведенных напряжений (условие Ишлин-ского – Ивлева).
Здесь рассмотрим классическую задачу Гадолина о сборке горячей посадкой двухслойной трубы. Отличие от случая [19], рассмотренного ранее, будет заключаться, во-первых, в максимально возможном приближении постановочной части задачи к техническим производственным условиям, а именно: до момента посадки охватывающая труба индуктивно разогревается по своей внутренней поверхности и, следовательно, в момент посадки имеем уже неоднородное по радиусу распределение температуры (в отличие от [19]). Во-вторых, в качестве условия пластического течения вместо классических условий максимальных касательных напряжений (условий Треска – Сен-Венана), принимаемых в [17, 19], будем использовать также кусочно-линейное классическое условие пластического течения максимальных приведенных напряжений [20, 21] (условие Ишлинского – Ивлева). Последнее вносит отличительные особенности [10] в методику расчетов. Новые области пластического течения могут в этом случае зарождаться не только на границах деформируемых тел, что неизменно отмечалось в условиях Треска – Сен-Венана [17, 19], но и внутри деформируемой области.
1. Соотношения математической модели. Постановка задачи
Здесь e i e j , e i p j – обратимые (термоупругие) и необратимые (пластические) составляющие полных деформаций e y ; u i - компоненты вектора перемещений; X, ц, 2
K = X + 3 ц - упругие постоянные; a - коэффициент линейного расширения; T , T 0 – текущая температура и температура свободного состояния тела (комнатная температура) соответственно. Второе соотношение из (1.1), где а у - компоненты тензора напряжений, называют законом Дюамеля – Неймана [2]. Его можно получить в качестве следствия закона сохранения энергии. Другим следствием этого закона является уравнение баланса энтропии; для плотности распределения энтропии s имеем
дМ = - J д t J
p T ijij
- T q j T j
J j =P sV j — T - 1 q j ; Vj
du
; £ p dtj
de i p j dt
(1.2)
В (1.2) qj , Jj – компоненты векторов потока тепла и энтропии; v i , £ P - компоненты вектора скорости и тензора скоростей пластических деформаций. Последнее слагаемое в (1.2) задает производство энтропии в необратимом процессе теплопроводности, предпоследнее – за счет процесса роста пластических деформаций в условиях принадлежности напряжений поверхности f ( a ij , k ) = 0 ( k - предел текучести) нагружения (текучести) в пространстве напряжений а у . Принимая условия принципа максимума Мизеса [20], имеем ассоциированный с поверхностью f ( a j , k ) = 0 закон пластического течения
= de p ф а f ( а у , k ) ;
dt да j,
ф> 0.
(1.3)
В качестве уравнения поверхности нагружения здесь будем использовать уравнение поверхности наклонной призмы Ивлева [21] в пространстве главных напряжений a i
В задаче Гадолина о сборке двухслойной металлической трубы допущение о малости деформаций e i e j не вызывает сомнений. Изменений формы деформируемых тел не происходит, а наибольшие объемные деформации задаются тепловым расширением по толщине труб. Тогда в прямоугольной декартовой системе координат в условиях изотропии в механических свойствах материала справедливы зависимости:
max | a i -
a= — k ; a =
3 a kk = 3 (а 1 +a 2 +a 3 ) . (1.4)
Заметим, что в качестве предела текучести k в (1.4) принимается предел текучести в опытах на чистый сдвиг. Его связь с температурой постулируем в виде f T - t ?
k = k o -^— . (1.5)
I T p - T o )
e j = 1 ( U , j + ui , i ) = e + e p ,
2 (1.1)
a = ( X 4 - 3a K ( T - T o ^ + 2 ц e ij .
Здесь k 0 – предел текучести при комнатной температуре T 0 ; Tp – температура плавления материала. Со-
гласно (1.2) получаем уравнения теплопроводности. Для такой цели полагаем изотропию в теплофизических свойствах материала, закон теплопроводности принимаем в форме Фурье. Уравнение теплопроводности следует записать в этом случае в виде
-
^0 = a 0 , j -58 kk + ( c^ ) - 1 ст е 8 p ; 0 = TTT . (1.6)
В (1.6) a – коэффициент температуропроводности; сl – удельная теплоемкость материала. Коэффициент связанности 5 для материала является малой величиной. Производством тепла за счет необратимого деформирования (последний слагаемый в (1.6)) будем также пренебрегать, считая его неизмеримо малым по сравнению с теплом, поступающим от внешних источников. В таком случае имеем несвязанную теорию, называемую теорией температурных напряжений.
Задача Гадолина является задачей сборки способом горячей посадки длинной трубы на такую же трубу. Чаще всего материалы труб одинаковы, но бывают и исключения. Перед посадкой охватывающую трубу R < r < R 2 следует нагреть. При крупногабаритных элементах сборки нагрев осуществляется подводом тепла к внутренней поверхности r = R охватывающей трубы. Поэтому рассмотрим первоначально температурную часть задачи теории температурных напряжений. Распределение температуры в этой теории находится отдельно и предварительно. В цилиндрической системе координат r , ф , z уравнение теплопроводности при сделанных допущениях в (1.6) запишется в виде
-
0 , t = a ( e , rr + r - 1e , r ) . (1.7)
Здесь индексом после запятой обозначена частная производная по данной независимой переменной. Краевыми и начальными условиями для (1.7) при предварительном нагреве охватывающей трубы будут соотношения:
0 , t ( R , t ) = q ( t ) ,
0 , r ( R , t ) = % 1 0 , (1.8) 0 ( r ,0 ) = 0
В (1.8) x 1 — коэффициент теплоотдачи от трубы в окружающую среду; он зависит от геометрии трубы, теплофизических свойств окружающей среды и др. Здесь будем считать х 1 постоянным. Перед моментом посадки t = t * подвод тепла к охватывающей трубе прекращается. Считаем, что в этот момент времени внутренний радиус охватывающей трубы R оказывается равным внешнему радиусу охватываемой R 1 ( R = R 1). Даже если это точно не выполняется, то выполнится за необходимо малое время до t * за счет остывания охватывающей трубы и нагрева охватываемой. Тогда, начи-
(1.9)
ная с момента посадки, уравнение (1.7) следует дополнить условиями:
0 (1) ( r , t * ) = g ( r ) при R 1 < r < R 2 , 0 (2) ( r , t * ) = 0 при R 0 < r < R1, 0 ( r ) ( R , t ) = X 1 0 (1) , 0 ( 2) ( R o , t ) = X 2 0 (2) , 0 (1) ( R 1 , t ) = 0 (2) ( R 1 , t ) ,
V 1 0 ( r ) ( R 1 , t ) = ^ 2 0 ( r 2) ( R 1 , t ) .
Здесь 0G ), 0 (2), v 1, V 2, X 1, X 2 — безразмерная температура, коэффициенты теплопроводности и коэффициенты теплоотдачи охватывающего и охватываемого элементов сборки соответственно; g ( r ) – рассчитанное в момент времени t = t * распределение температуры по охватывающей трубе. Неизменность граничных R 2 и R 0 поверхностей сборки при нагревании в (1.9) связана с последовательным использованием допущения о малости деформаций.
Для расчетов распределений температуры численным решением задач (1.7)–(1.8) или (1.7)–(1.9) препятствий не существует. Имеем для этого ряд отработанных вычисленных алгоритмов и программ расчетов. Для целей настоящей работы удобны вычисления последовательными шагами по времени, так как именно такими шагами будут рассчитываться и напряженно-деформированные состояния. Далее будем считать, что в каждый рассматриваемый момент времени распределение температуры по материалам сборки известно (найдено) на каждом последовательном временном шаге расчетов.
-
2. Деформирование охватывающей трубы до момента посадки
Обратимся к схеме (рис. 1), где фиксируются возникающие и исчезающие области пластического течения. Данная схема эволюции областей пластического течения, диктуемая эволюцией напряженных состояний, является итогом расчетов. Приводим ее в начале изложения только с целью более ясного дальнейшего представления. Итак, с момента начала нагрева t = 0 материал трубы деформируется обратимо (термоупруго) (рис. 1, а ) до некоторого (рассчитываемого) момента времени t = t 1 > 0, когда на граничной поверхности r = R трубы выполнится условие пластического течения в форме 2о r -оф -ст z = 4 к . На рис. 2 представлено сечение поверхности текучести (1.4) девиаторной плоскостью ст r + стф + ст z = 0 . Грань поверхности текучести, указываемая на рис. 1, соответствует такому же отрезку прямой на рис. 2. Упругопластическая граница r = и 1 ( t ) в своем продвижении (направление движения на рис. 1
указывается стрелками) по материалу трубы оставляет за собой область пластического течения R < r < n 1 ( 1 ) .
В некоторый последующий момент времени 1 = 12 > 11 на упругопластической границе r = n1 (1) наряду с условием 2 стr -стф-стz = 4к выполняется еще и условие стr + стф - 2стz = 4к, т.е. выполняются условия ребра призмы Ивлева. Расчеты показывают, что с момента 1 = 12 на поверхности r = n1 (1) рождаются две граничные поверхности (рис. 1, в). Одна из них r = n3 (1) является новой упругопластической границей и, опережая r = n1 (1), движется далее к внешней поверхности трубы. Она оставляет за собой пластическую область n2 (t)< r < n3 (t), где течение происходит в соответствии грани стr + стф - 2стz = 4к призмы Ивлева. Граница r = n1 (t) этой области продолжает продвигаться по материалу, но теперь она оказывается граничной поверхностью, разделяющей область пластического течения. В таком же качестве выступает граничная поверхность r = n2 (t), которая движется в обратную сторону к внутренней поверхности трубы. Область пластического течения таким способом поверхностями r = n1 (t) и r = n2 (t) разделяется на три части (см. рис. 1, в), в которых течение подчинено разным системам уравнений из-за того, что в них выполнены различные требования условий пластического течения.
Спустя некоторое время при 1 = 1 3 > 1 2 поверхность r = n 2 ( t ) выходит на границу r = R и одна из областей пластического течения исчезает (рис. 1, г ). Деформирование с двумя R < r < n 1 ( t ) и n 1 ( t ) < r < n 3 ( t ) областями пластического течения продолжается далее до момента времени 1 = 1 4 > 1 3, когда нагрев прекращается.
За технологический промежуток времени от 1 = 1 4 до момента посадки t * пластическое течение в деталях сборки прекращается, но это процесс со своими знаковыми моментами времени. Так, в момент времени 1 = 1 4 на границе трубы r = R зарождается и продвигается внутрь тела новая граничная поверхность r = n 4 ( 1 ) , которая, разделяя область течения, оставляет за собой область, где течение происходит согласно условию ст r +стф- 2ст z = 4 к , т.е. в соответствие уже не ребру, а грани поверхности текучести (рис. 1, д ). Быстро продвигаясь, граница r = n 4 ( t ) настигает поверхность r = n 1 ( t ) .
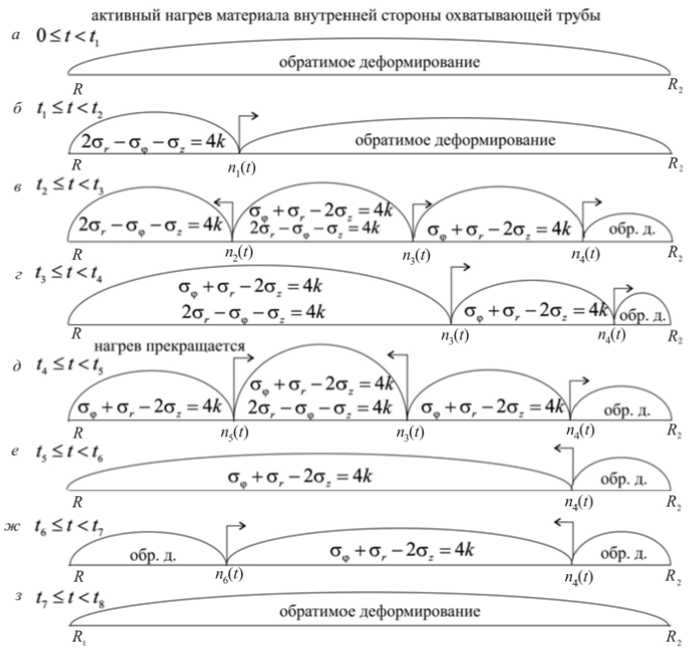
Рис. 1. Схема возникновения и исчезновения областей пластического течения в материале охватывающей трубы
Fig. 1. Diagram of the emergence and disappearance of plastic flow regions in the material of the enclosing pipe
Начиная с этого момента времени t = t 5 > t 4 во всей пластической области ) < г < n 3 ( t ) течение происходит в соответствие грани ст r + ст ф - 2ст z = 4 к наклонной призмы, поверхность которой является поверхностью текучести в трехмерном пространстве ст r , стф, ст z . Последующий момент времени t = 1 6 > 1 5 (рис. 1, е )) порождает разгружающую упругопластическую границу r = n 5 ( t ) . Продвигаясь, последняя встречает поверхность r = n 3 ( t ) (она меняет направления движения) при t = t 7 > t 6 , и после этого пластические области исчезают, а материал охватывающей трубы во всем своем объеме деформируется обратимо.
Уже отмечалось, что расчеты проводим последовательными шагами по времени. Первоначально материал трубы деформируется обратимо. Для деформаций и напряжений согласно (1.1) в цилиндрических координатах имеем:
e = e p = e z = 0; e r = e r = и , r ; e = e e = r - 1 u r , ст r = ( X + 2 ц ) er + X e ф - 3 a KT 0 9 ,
ф стф = (X + 2ц)eф+Xer -3aKT09, ст r = X (er + eф) - 3a KT09.
Подстановка (2.1) в уравнение равновесия стr,r + r-1 (стr -стф) = 0
приводит к обыкновенному (время t выступает в квази-статической задаче в качестве параметра) дифференциальному уравнению
8 Г 1 8 Л aKT 89 —I (rur) I =
8 r ^ r 8 rv J X + 2 ц 8 r
Полагая в рассматриваемый момент времени распределение температуры 9 ( r ) известным (найденным решением температурной задачи), после интегрирования (2.3) находим:
3 a KT r r ^n/X C 211 ( t )
u = ------— x 9( x, t) dx + — CГ1' (t) + r (X + 2ц) r) V ’2 стr = (X + ц)C1 (t) - 2цr2C211 (t) - 6aцT0 jx9(x, t)dx, стф = (X + ц) С (t) + 2ц r2 C211 (t) +
+ 6aцK (X + ц)-1 T | J x9(x, t) dx - 9 (r, t) |, RJ ст z = X C'11 (t) - 6aцK (X + ц)-1 T09( x, t).
В рассчитываемый момент времени значения функций C(1) (t) и C (t) находим, выполняя граничные условия стr (),t) = стr ()2,t) = 0. Наличие зависимос- тей (2.4) позволяет обойтись при решении механической части задачи без дискретизации расчетной области и использования приближенных методов расчетов. Здесь покажем, что подобное справедливо для любых областей как пластического течения, так и обратимого деформирования при наличии накопленных необратимых деформаций.
Продолжая расчеты последовательными шагами по времени, приходим к моменту времени t = t 1, когда при r = ) 1 образуется область пластического течения с упругопластического границей r = n1 ( t ) . Соотношения закона Дюамеля – Неймана задают зависимости:
стr = (X + 2ц)(ur,r - erp) + X (r-1 ur - еф - epp) - 3aKT09, стф =(X + 2ц)(r-1 ur -ep) + X(ur,r -erp -epp)-3aKT09, (2.51 стr = (X + 2ц)(-ez ) + X(urr -erp + r-1 ur -ep)-3aKT09.
Необратимые деформации исключаются из (2.5) с помощью ассоциированного с гранью 2стr -ст^-стz = 4к поверхности текучести закона пластического течения. Таким способом уравнение равновесия (2.2) приобретает форму d2ur , 1 дur uur 2 Г2дк _ к) , , т 89
—r +--- - h -r- = |---+ —I + 3 a T 0—, (2.61
-
8 r 2 r 8 r r 2 3 K ( 8 r r J 8 r
, 1 3X + 5ц h = , ---------- .
-
\ 3X + 2ц
Полагаем, что распределение температуры 9(r, t) в данный момент времени уже рассчитано. Интегрируя (2.6), найдем ur (r, t) = 1,5h-1 ((h + 1)Ф(r, 5, h) + (h - 1)Ф(r, 5, -h)) +
+ ( 3 Kh ) ( ( 2 h - 1 ) V ( r , 5 , h ) - ( 2 h + 1 ) ^ ( r , 5 , - h ) ) -
-
- ( 2 hrh ) - 1 C <21 ( t ) + rhC 221 ( t ) ,
ст r = 1,5 K ( hr ) 1 ( h 2 - 1 ) ( ф ( r , 5 , - h ) -Ф ( r , 5 , h ) ) -
-
- ( 3 hr ) 1 ( ( h - 1 )( 2 h - 1 ) ^ ( r , 5 , h ) + ( h + 1 )( 2 h + 1 ) ^ ( r , 5 , - h ) ) +
-
+ ( h - 1 ) ( 2 hr h + 1 ) ' KC ® ( t ) + ( h + 1 ) ( r h ') KC® ( t ) ,
стф = -V ( r , 5 , - h ) ( 3 Krh )- 1 ( 2 h + 1 ) ( K ( h + 1 ) + ц ) -
-
-Y ( r , 5 , h )( 3 Krh ) ' ( 2 h - 1 ) ( K ( 1 - h ) + ц ) +
+ 1,5 Ф ( r , 5 , - h )( h - 1 )( rh ) 1 ( K ( h + 1 ) + ц ) +
+ 1,5 Ф ( r , 5 , h )( h + 1 )( rh )- ( K ( 1 - h ) + ц ) - 1221
- 2 к - ( K ( 1 - h ) + ц ) ( 2 hr h + 1 ) ' C '21 ( t ) +
+ (K (h + 1) + ц)( rh-1) C221 (t), er =-2e^p = 2aT09-2(2ц + X)(3цK) ' к +
+ ( 4 h 2 - 1 ) ( 9 Khr )- 1 ( V ( r , 5 , h ) -V ( r , 5 , - h ) ) +
+ ( 2 hr ) 1 ( ( h - 1 )( 2 h - 1 ) Ф ( r , s , - h ) - ( h + 1 )( 2 h + 1 ) Ф ( r , s , h ) ) + + ( 2 h + 1 ) ( 6 hr h + 1 ) " ' C 1(2) ( t ) + 3 — 1 ( 2 h - 1 ) ( rh - 1 ) C 22) ( t ) .
Ф ( r , s , h ) = a T 0 r - h j p h e ( p ) d p ; ^ ( r , s , h ) = r - h j p h k ( p ) d p ; s = R .
ss
На каждом временном шаге расчетов теперь следует определить значения четырех функций С1 (t), С21) (t), C2 (t), с22) (t) и положение в этот момент времени упругопластической границы n1 (t). Для этой цели име ем условия отсутствия напряжения ar на граничных поверхностях r = R и r = R2, а также условия непре рывности перемещения ur, напряжения ar на продви гающейся поверхности r = n1 (t) и выполнения на ней условия пластического течения. Такую систему алгебраических соотношений приходится разрешать на каждом шаге расчетов. С появлением новых областей течения порядок подобной системы уравнений будет расти. Далее на этом останавливаться не будем, но заметим, что подобные значения и рассчитываемые положения поверхностей, делящих область деформирования на части, всегда имеют для своего определения необходимое число граничных условий и условий на продвигающихся граничных поверхностях.
После момента времени t = 12 область пластического течения разделяется уже на три части (см. рис. 1, в)). В части R < r < n2 (t) справедливыми остаются зависи- мости (2.7). Аналог (2.7) для области течения
П (t)< r < n3 (t) следует записать, заменив уравнение грани призмы текучести (призмы Ивлева) на иное – ar +стф - 2az = 4к (см. рис. 1, 2). Эти действия не несут в себе дополнительных сложностей и позволяют записать ur !; (Т( r, s ^^С r, s,
3 K
^^^^^^в
C (3) ( t )
- a T o e( r )---- p ф ( r ) , s = n 1 ( t ) .
3 K
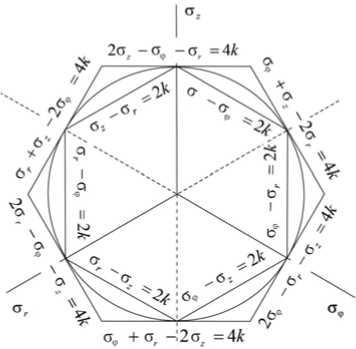
Рис. 2. Сечение поверхности текучести в девиаторной плоскости
Fig. 2. The cross section of the fluidity surface in the deviator plane
В области П 2 ( t ) < r < n ( t ) пластическое течение происходит в соответствие напряжений ребру поверхности текучести в пространстве главных напряжений (см. рис. 2). Оно образовано пересечением граней 2a r - аф - a z = 4 к и a r + аф - 2a z = 4 к . На этом ребре призмы Ивлева a r -aф = 4/3 к . Уравнение равновесия (2.2) в данном случае интегрируется (задача оказывается статически определимой). Ассоциированный закон пластического течения вместе с условиями пластичности приводят к зависимостям:
ur
Ф ( r , s ,1 ) + ц
—------- ^ ( r , s ,1 ) +
3(К + ц) ( ’ ’ )
+ 2 rc;-> ( t ) +
c 24) ( t )
r
+ 3Ф(r,s,1) + ^C? (t) + C3^, 2Kr a r =- 3r ^( r, s,-1) + CP ( t ) ,
О ф =- 4- V ( r , s , - 1 ) - 4 к ( r ) + C ™ ( t ) , 3 r 3
(2.8)
a r
a ф
x v( r , s ,1 ) + ц )
+ KC ,(4) ( t ) -
6 ц К r ( к + ц )
2 ц C 24) ( t )
r 2 ,
Ф ( r , s ,1 )
+
a z = - ^ ( r , s , - 1 )- 8 k ( r ) + C 1(3) ( t ) , 3 r 3
2 fX + 2ц)
e r = - 3 r - 1 Ф ( r , s ,1 ) + 2 a T o e ( r ) - ) к ( r ) +
3 ц К
. 4ц J к ( r ) - 3 ( К + ц )( 1 '
V ( r , s ,1 ) 2 ------- 1 + r J
(2.9)
p еФ
+ 3 rK ( V( r , s ,1 ) - 3 V( r , s , -
+ J6S K r£ C r , s ,1 ) -a T e ( r ) )+
К + ц( r 0 V 7J 2 ц C <4) ( t) + KC ,(4) ( t ) + ц r 2 k ) ,
C ,(3) ( t ) C 23) ( t )
+--- —--7^ - pr ( r )
6 Kr 2 r
e r ( r , t ) =
a T o К
2 ( К + ц )
e( r)
X + 2 ц 3 ц ( к + ц )
s = n 1 ( t ) .
= ^ ( r , s , - 1 ) +
9Kr ( )
2(3 K + 2ц)
-( к ( r ) - 9 ц К
к ( r ) + 6 C ,(4) ( t ) ,
Зависимости (2.9) включают в себя необратимые деформации pr (r) и рф(r), которые были накоплены
в условиях пластического течения, предваряющего течение в соответствие ребру поверхности текучести максимальных приведенных напряжений. Перед продвигающейся поверхностью r = п 1 ( t ) течение осуществляется при соответствии напряжений грани ст r + стф 2ст z = 4 к наклонной призмы Ивлева, а перед поверхностью r = п 2 ( t ) - грани 2ст r -стф -ст z = 4 к этой призмы. Таким образом, p r ( r ) и p ф( r ) в области П2 ( t ) < r < « 1 ( t ) являются пластическими деформациями, произведенными в условиях течения при 2ст r - стф - ст z = 4 к до момента времени t = t * > t2, когда данной поверхности достигает граница r = п 2 ( t ) . Ина
*
че pr ( r ) = e r I r , t ) , p ф ( r ) = е ф I r , t ) и t является моментом прихода в данную точку материала упругопластической границы. Это разные моменты времени для разных точек тела. Далее при t > t * эти накопленные пластические деформации со временем не меняются. В иных условиях пластического течения, в данном конкретном случае в условиях соответствия напряжений ребру поверхности текучести, p r ( r ) и p ф ( r ) предстают в качестве начальных условий для дальнейшего изменения со временем e r ( r , t ) и е ф ( r , t ) в области n 2 ( t ) < r < п 1 ( t ) . Это же относится к области течения n 1 ( t ) < r < n 3 ( t ) . Алгоритм расчетов должен предусмотреть способ формирования подобных массивов, не изменяющихся со временем необратимых деформаций, и их использование в дальнейших расчетах. Далее на подобной операции специально останавливаться не будем; она всегда имеет место, если только граничная поверхность движется в область, где пластическое течение происходило. Это касается и разгружающих упругопластических границ. Несмотря на то, что за такими поверхностями деформирование обратимо, происходит оно в присутствии неизменяющихся необратимых деформаций. Соотношения (2.1) и (2.3) в таком случае обязаны содержать слагаемые, задаваемые такими деформациями.
Соотношения (2.7)–(2.9) включают в себя шесть неизвестных функций времени С 1(2) , С 2(2) , С 1(3) , С 2(3) , С 1(4) , С 1(4) . К ним необходимо добавить еще С 1(1) , С 2(1) , n 1 , n 2 , n 3 . Следовательно, на каждом шаге расчетов, исходя из граничных условий и условий на продвигающихся поверхностях, делящих область пластического течения, требуется сформировать и разрешить систему 11 алгебраических уравнений.
Последующие расчеты покажут, что поверхность r = п2 (t) перемещается быстрее остальных и достигает границы трубы r = R в некоторый момент времени t = 13 (рис. 1, г). При t > 13 остаются три области де формирования. В области n3 (t) < r < R2 материал деформируется обратимо в соответствии с зависимостями (2.4). В областях п2 (t) < r < n3 (t) и R < r < пц (t) справедливы зависимости (2.8) и (2.9) соответственно. При таком продолжающемся деформировании трубы удается достичь температуры на поверхности r = R, определенной техническими условиями операции сборки горячей посадкой. Нагревание прекращается, и за время подготовки операции посадки происходят процессы, связанные с разгрузкой материала трубы. На рис. 1 быстрый процесс разгрузки иллюстрируется промежутком времени от момента времени t = 14, когда нагрев прекращается, до момента посадки t = 18 > 14. Расчетами установлено, что в момент времени t = 14 от граничной поверхности r = R отделяется и распространяется по материалу поверхность r = п5 (t). Вслед за моментом исчезновения пластической области п5 (t)< r < п3 (t) на поверхности r = R образуется разгружающая упругопластическая граница r = п6 (t), которая в своем последующем движении (см. рис. 1) оставляет за собой область обратимого деформирования R < r < п6 (t). Из-за наличия в этой области неизменяющихся пластических деформаций зависимости (2.1) и (2.4) оказываются несправедливыми. Следует получить интегрированием уравнения равновесия новые зависимости, учитывающие накопленные прежде необратимые деформации. В отличие от (2.3) уравнение равновесия в области R < r < п6 (t) теперь принимает форму df 1 д(rUr)) aKT0 59 2ц / х
II =( pv - p,x ) + дr ^r дr J Х + 2ц дr (Х + 2ц) r' ф^
. д p r , ^ д / , х
+ е7+Г+2Д er(p'+p-) • <2л0> pr (r) = er (r, t *); p ф (r) = eф (r, t *);
pz ( r ) = e z ( r , t * ) .
Интегрированием (2.10) получаем распределение перемещения ur в зависимости от распределения температуры в рассчитываемый момент времени и, следовательно, распределения в этот момент времени деформаций и напряжений. Из-за громоздкости этих конечных зависимостей здесь их не выписываем. На каждом шаге таких расчетов, как и всюду ранее, приходится пересчитывать значения постоянных, появившихся после интегрирования (2.10), и положения продвигающихся граничных поверхностей.
-
3. Деформирование после момента посадки
Моментом посадки считаем последующий момент времени t = 18 = t* (рис. 3, ж)), когда внутренний ради- ус охватывающей трубы равен внешнему радиусу охватываемой (R = R1). Первоначально при 1 > 1* сборка деформируется обратимо согласно уравнениям равновесия (2.10) для охватывающего и (2.3) для охватываемого элементов сборки. Но на некотором последующем шаге расчетов 1 = 19 на границе r = R1 охватывающей трубы зарождается повторное (обратное) пластическое течение в условиях грани 2ar -аф-аz = -4к призмы Ивлева (рис. 3, б). Уравнение равновесия в области повторного пластического течения R < r < n6 (1), где r = n6 (1) — уравнение продвигающейся упругопластической границы, будет вполне аналогично (2.10), если в нем учесть обратность пластического течения (изменение знака правой части в условии течения). Проинтегрировав его, найдем ur = 1,5 h1 ((h +1)®( r, s, h) + (h -1)®( r, s, - h ))
-
- ( 3 Kh )- 1 ( ( 2 h - 1 ) Q ( r , s , h ) + ( 2 h + 1 ) Q ( r , s , - h ) ) +
+ц ( 2 Kh ) 1 ( ^ ф ( r , s , - h ) -^ ф ( r , s , h ) +
+V 2 ( r , s , - h ) - V z ( r , s , h ) ) - ( 2 hr h ) - 1 C (6) ( 1 ) + rhC 26) ( 1 ) ;
a r = 1,5 K ( hr ) 1 ( h 2 - 1 ) ( ® ( r , s , - h ) -® ( r , s , h ) ) +
+ ( 3 hr ) 1 ( ( h - 1 )( 2 h - 1 ) ^ ( r , s , h ) -
-
- ( h + 1 ) ( 2 h + 1 ) ^ ( r , s , - h ) ) +
+ Ц ( h + 1 ) ( 2 hr | ' ( V z ( r , s , - h ) - Т ф ( r , s , - h ) ) +
+ ц ( h - 1 )( 2 hr | ' ( V z ( r , s , h ) -Т ф ( r , s , h ) ) +
+ ( h - 1 ) ( 2 hr h + 1 ) ' KC 1(6) ( 1 ) + ( h + 1 ) ( rh ' ) KC 26) ( 1 ) ;
(3.1)
аф = Q ( r , s , - h )( 3 Krh ) " ’ ( 2 h + 1 ) ( K ( h + 1 ) + ц ) +
+ П ( r , s , h )( 3 Krh ) ( 2 h - 1 ) ( K ( 1 - h ) + ц ) + ц ( pz - p ф ) + + ( V z ( r , s , - h ) -Тф ( r , s , - h ) ) ( 3 Krh ) 1 ( 2 h + 1 ) x
x ( K ( h + 1 ) + ц ) + ( Т ф ( r , s , h ) -V z ( r , s , h ) ) x x ( 3 Krh ) ( 2 h - 1 ) ( K ( 1 - h ) + ц ) +
+ 1,5 ® ( r , s , - h )( h - 1 )( rh ) 1 ( K ( h + 1 ) + ц ) +
+ 1,5 ® ( r , s , h )( h + 1 )( rh ) 1 ( K ( 1 - h ) + ц ) -
-
- 2 к - ( K ( 1 - h ) + ц ) ( 2 hr h + 1 ) C 1(6) ( 1 ) +
+ ( K ( h + 1 ) + ц ) ( r h - 1 ) C^ ( 1 ) ;
e r =- 2 е ф = 2 0 + 2 ( 2 ц + Х )( 3 ц K )- 1 к - ( 4 h 2 - 1 ) x x ( 9 Khr ) 1 ( Q ( r , s , h ) -^ ( r , s , - h ) ) + + ( 2 hr ) ' ( ( h - 1 )( 2 h - 1 ) ® ( r , s , - h ) -
-
- ( h + 1 ) ( 2 h + 1 ) ® ( r , s , h ) ) + ( 2 h + 1 ) ( 6 hr h + 1 ) - 1 C 1(6) ( 1 ) +
+ 3 1 ( 2 h - 1 ) ( rh ' ) C 26) ( 1 ) - pr + ц ( 2 h - 1 ) ( 6 rhK )- 1 x x ( V z ( r , s , - h ) - Тф ( r , s , - h ) ) +
+ ц ( 2 h + 1 )( 6 rhK | ' ( V z ( r , s , h ) - V ( r , s , h ) ) .
Последовательность появления и исчезновения областей пластического течения представлена схематически на рис. 3, а–ж вместе с характерными моментами времени ( 1 8 - 1 14 ) . Стрелками указаны направления движения упругопластических границ. Необратимое деформирование охватываемой детали сборки начинается в момент расчетов 1 10 > 1 9 и связано с выполнением условия 2a r -аф a z = 4 к .

Рис. 3. Схема возникновения и исчезновения областей пластического течения в условиях сборки и последующего ее остывания
Fig. 3. Scheme of the appearance and disappearance of plastic flow regions under assembly conditions and its subsequent cooling
Зависимости распределения напряжений и деформаций от распределения температуры в каждый момент времени даются формулами (2.7), в которых следует принять s = n 7 ( t ) . Такие зависимости для области n 8 ( t ) < r < R аналогичны и следуют после интегрирования уравнения вида (2.10). Следовательно, какие бы области пластического течения ни появлялись, всегда можно получить конечные зависимости, связывающие в каждый рассчитываемый момент времени распределения температуры с распределением по сборке деформаций и напряжений.
На рис. 4 показано распределение напряжений в текущий момент времени t e ( t 10, t n) . С целью полноты расчетов, когда учитывается возникновение всех возможных областей пластического течения, геометрические размеры и термомеханические постоянные материалов элементов сборки были выбраны следующими: R = 0,06 м, R 1 = 0,08 м, R 2 = 0,1 м; для охватывающей детали сборки р = 2,8 -10 3 кг/м3, ср = 0,922 кДж/(кгК), Х = 10 Вт/(м2К), ф = 130 Вт/(мК), Е = 72 ГПа, v = 0,3, к = 255 МПа, T p = 660 °С; для охватываемой трубы р = 2,7 -103 кг/м3, ср = 0,903 кДж/(кгК), х = 10 Вт/(м2К), Ф = 188 Вт/(мК), Е = 70 ГПа, v = 0,3, к = 210 МПа, T p = 660 °С.
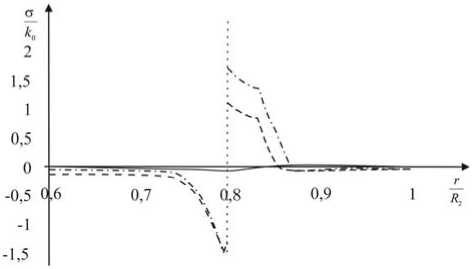
Рис. 4. Распределения напряжений в материале сборки
Fig. 4. Stress distributions in the material of the assembly
Сплошной линией на рис. 4 обозначена безразмерная компонента напряжений a r , штриховой - стф,, штрихпунктирной - a z . Эти обозначения сохраняются и для рис. 5, 6. На рис. 5 показано распределение остаточных напряжений в случае, когда нагревом на внутренней поверхности охватывающей трубы достигалась температура T = 400 ° С. Для сравнения на рис. 6 указывается распределение по сборке остаточных напряжений, когда до посадки температура по охватывающей детали распределена однородно T ( r ) = 400 ° С - const.
Натяг в сборке в рассматриваемом случае оказался значительно меньшим и равным 41 МПа. В случае однородного нагрева (см. рис. 6) натяг в сборке 83 МПа.
Для обеспечения последнего в рассматриваемом случае требуется более интенсивный нагрев поверхности r = R .
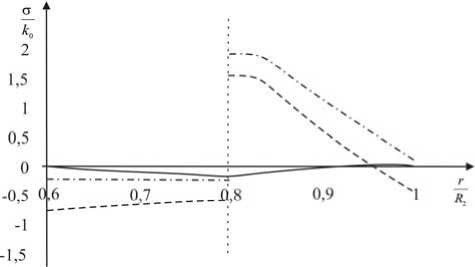
Рис. 5. Распределения остаточных напряжений в материале сборки
Fig. 5. Residual stress distributions in the assembly material
При ином выборе параметров задачи некоторые пластические области могут не появляться. Однако других областей пластического течения, изменяя геометрию задачи, свойства материалов сборки и уровень нагрева, получить невозможно. В этом заключается полнота расчетов. Появляются и исчезают только такие пластические области, которые представлены на рис. 1, 2.
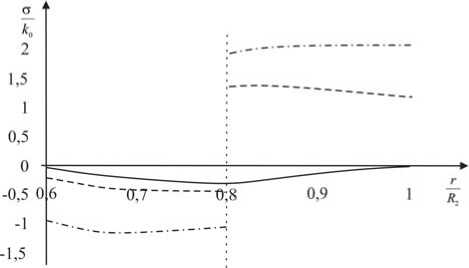
Рис. 6. Распределения остаточных напряжений в материале сборки
Fig. 6. Residual stress distributions in the assembly material
Заключение
Полученное решение задачи Гадолина для упругопластических материалов элементов сборки является численно-аналитическим. В рассмотренном случае возможно записать решение в аналитической форме. Для этого достаточно записать в аналитическом виде решение температурной части задачи, что в данном случае возможно, и воспользоваться аналитическими зависимостями, которые здесь получены. Однако в таком случае для каждого временного промежутка, на которые разбивается технологическая операция (см. рис. 1, 3), имели бы набор необозримых зависимостей и формул, анализировать которые снова пришлось бы численно. Следовательно, предложенный метод расчетов последовательными шагами по времени позволяет избежать утомительных аналитических расчетов. С другой стороны, таким способом удается обойтись без использования приближенных методов расчета, опирающихся на дискретизацию расчетных областей. В условиях изменяющихся границ расчетных областей, появления новых областей пластического течения и исчезновения старых потребуются специальные алгоритмические приемы, позволяющие отслеживать эти изменения, что приводит к усложнению приближенных методов (сеточных, конечно-элементных) расчетов.
Важно отметить, что полученное численно-аналитическое решение является полным, поскольку иных (новых) областей пластического течения в рамках описанной постановки задачи появиться не может. Однако при других условиях в геометрии элементов сборки, степени нагрева, механических свойствах материалов некоторые пластические области могут не появиться. При нагреве охватывающей трубы, обеспечивающем требуемый натяг в сборке, проявляется повторное (обратное) пластическое течение для всех исследуемых конструкционных материалов как в рамках условия пластич- ности Ишлинского – Ивлева, так и при условии пластического течения Треска – Сен-Венана.
Список литературы Эволюция температурных напряжений в задаче Гадолина о сборке двухслойной упругопластической трубы
- Берникер Е.И. Посадка с натягом в машиностроении. – Л.: Машиностроение, 1966. – 168 с. 2. Боли Б., Уэйнер Дж. Теория температурных напряжений. – М.: Мир, 1964. – 517с.
- Карноухов В.Г. Связанные задачи термоупругости. – Киев: Наукова думка, 1982. – 206 с.
- Lippmann H. The effect of a temperature cycle on the stress distribution in a shrink fit // Intern. J. Plasticity. – 1992. – Vol. 8. – P. 567–582.
- Гаффаров Р.Ф., Щенятский А.В. Применение метода конечных элементов для повышения нагрузочной способности соединений, собираемых термическим методом // Высокие технологии. – 2004. – Вып. 3. – С. 162–167.
- Александров С.Е., Ломакин Е.А., Дзенг Й.-Р. Решение термоупругопластической задачи для тонкого диска из пластически сжимаемого материала, подверженного термическому нагружению // ДАН. – 2012. – Т. 443, № 3. – С. 310–312.
- Александров С.Е., Лямина Е.А., Новожилова О.В. Влияние зависимости предела текучести от температуры на напряженное состояние в тонком полом диске // Проблемы машиностроения и надежности машин. – 2013. – № 3. – С. 43–48.
- Шевченко Ю.Н., Стеблянко П.А., Петров А.Д. Численные методы в нестационарных задачах теории термопластичности // Проблемы вычислительной механики и прочности конструкций. – 2014. – Вып. 22. – С. 250–264.
- Буренин А.А., Дац Е.П., Мурашкин Е.В. Формирование поля остаточных напряжений в условиях локального теплового воздействия // Изв. РАН МТТ. – 2014. – № 2. – С. 124–131.
- Температурные напряжения в упругопластической трубе в зависимости от выбора условия пластичности / Е.П. Дац, Е.В. Мурашкин, А.В. Ткачева, Г.А. Щербатюк // Изв. РАН. МТТ. – 2018. – № 1. – С. 32–43.
- Gamer U.F. concise treatment of the shrink fit withelastic plastic hab // Int. J. Solids. Struct. – 1992. – Vol. 29. – P. 2463–2469.
- Mack W. Thermal assembly of an elastic–plastic hub and a solid shaft // Arch. Appl. Mech. – 1993. – Vol. 63. – P. 42–50.
- Bengeri M., Mack W. The influence of the temperature dependence of the yield stress on the stress distribution in a thermally assembled elastic-plastic shrink fit // Acta Mechanica. – 1994. – Vol. 103. – P. 243–257.
- Kovacs А. Residual Stresses in Thermally Loaded Shrink Fits. Periodica Polytechnica. Ser. Mech. Eng. –1996 – Vol. 40, № 2. – P. 103–112.
- Дац Е.П., Ткачева А.В., Шпорт Р.В. Сборка конструкции «кольцо в кольце» способом горячей посадки // Вестник ЧГПУ им. И.Я. Яковлева. Серия: Механика предельного состояния. – 2014. – № 4(22). – С. 204–213.
- Дац Е.П., Ткачева А.В. Технологические температурные напряжения в процессах горячей посадки цилиндрических тел при учете пластических течений // ПМТФ. –2016. – Т. 57, № 3(337). – С. 208–216.
- Буренин А.А., Ткачева А.В., Щербатюк Г.А. К расчету неустоявшихся температурных напряжений в упругопластических телах // Вычислительная механика сплошных сред. – 2017. – Т. 10, № 3. – С. 245–259.
- Буренин А.А., Матвеенко В.П., Ткачева А.В. Температурные напряжения в процессе сборки двухслойного вала способом горячей посадки // Ученые записки Комсомольскогона-Амуре государственного технического университета. – 2018. – № 3 (35). – С. 31–41.
- Буренин А.А., Ткачева А.В. О сборке двухслойной металлической трубы способом горячей посадки // Изв. РАН. МТТ. – 2019. – № 3. – С. 86–99.
- Быковцев Г.И., Ивлев Д.Д. Теория пластичности. – Владивосток: Дальнаука, 1998. – 528 с.
- Ишлинский А.Ю., Ивлев Д.Д. Математическая теория пластичности. – М.: Физматлит, 2001. – 704 с.
- Bland D.R. Elastoplastic thick-walled tubes of workhardening material subject to internal and external pressures and to temperature gradients // J. of the Mechanics and Physics of Solids. – 1956. – Vol. 4. – P. 209–229.
- Sen S., Aksakal B. Stress analysis of interference fitted shaft–hub system under transient heat transfer conditions // Materials and Design. – 2004. – Vol. 25. – P. 407–417.
- Stress analysis of shrink-fitted joints for various fit forms via finite element method / A. Ozel, S. Temiz, M. Demir Aydin, S. Sen // Materials and Design. –2005. – Vol. 26. – P. 281–289.
- Truman C.E., Booker J.D. Analysis of a shrink-fit failure on a gear hub/shaft assembly // Engineering Failure Analysis. – 2007. – Vol. 14. – P. 557–572.
- Antoni N., Gaisne F. Analytical modelling for static stress analysis of pin-loaded lugs with bush fitting //Applied Mathematical Modelling. – 2011. –Vol. 35. – P. 1–21.
- Apatay T., Arslan E., Mack W. Effects of homogeneous and inhomogeneous heating on rotating shrink fits with annular inclusion and functionally graded hub // Journal of thermal stresses. – 2019. – Vol. 42, № 11. – P. 1458–1479.
- Doležel I., Kotlan V., Ulrych B. Design of joint between disk and shaft based on induction shrink fit // Journal of Computational and Applied Mathematics. – 2014. – Vol. 270. – P. 52–62.
- Siemiątkowski Z., Rucki M., Lavrynenko S. Investigations on the modeled shrink fitted joints of assembled crankshafts // J. Mach. Constr. Maint. –2018. – Vol. 108. – P. 33–44.
- Apatay T., Arslan E., Mack W. Thermally loaded elasticplastic shrink fit with FGM-Hub // Proc. Appl. Math. Mech. – 2017. – Vol. 17, № 1. – P. 285–286.


