Эволюционный алгоритм оптимизации распределительной электрической сети

В электросетевом хозяйстве страны насчитывается 2,5 млн км высоковольтных линий электропередачи. Из них 1,5 млн км составляют воздушные линии распределительных сетей напряжением 6 и 10 кВ, на которые приходится около 70 % нарушений электроснабжения потребителей [6]. При проектировании таких сетей необходимо учитывать следующие особенности:

• 1.    Большинство сетей имеет древовидную конфигурацию, образованную радиальными и магистральными линиями электропередачи, сходящимися в распределительных пунктах и трансформаторных подстанциях.

• 2.    На местности нет участков, на которых запрещено строительство воздушных линий электропередачи.

• 3.    Согласно «Правилам устройства электроустановок», при передаче от источника потребителям не допускается падение напряжения ниже предельно допустимого уровня от номинального напряжения. Обычно это ограничение проверяется у удаленных потребителей [9].

• 4.    Привязка элементов сети к условиям местности: неоднородность местности влияет на величину необходимых капитальных вложений.

Для оптимизации проектирования таких сетей можно применять модель потоковой задачи Штейнера (она инвариантна относительно направления потоков). Эта задача – одно из обобщений классической задачи Штейнера [1], которая относится к классу NP -трудных [2]. Для их решения широко используют приближенные методы, в частности эволюционные. Данная статья обосновывает применение потоковой задачи Штейнера к распределительным электрическим сетям и представляет эволюционный алгоритм (ЭА) для ее решения.

Модель потоковой задачи Штейнера . При проектировании распределительной электрической сети известно расположение фиксированных точек: источника (понизительной подстанции) и потребителей с расчетными мощностями. Тре

буется связать их сетью линий электропередачи с минимальными затратами на ее строительство и эксплуатацию. Для минимизации можно вводить дополнительные свободно размещаемые точки – распределительные узлы.

Математическая модель потоковой задачи Штейнера представляет схему искомой сети в виде ориентированного корневого дерева. Терминальные вершины дерева отождествляются с фиксированными точками (корень – с источником), а точки Штейнера (ТШ) – с распределительными узлами. С дугами дерева сопоставляются линии электропередачи. На дугах задается весовая функция, зависящая от величин потоков на них. Весом дуги называют значение весовой функции, отнесенное к единице длины дуги, а ее взвешенной длиной – произведение веса на длину дуги в евклидовой метрике. В общем случае весовая функция может быть произвольного вида, но должна быть неубывающей. Ищется сеть с минимальной суммой взвешенных длин дуг.

Дерево описывают топология (порядок соединения вершин) и координаты ТШ. Локально оптимальным решением задачи является дерево Штейнера (ДШ) – дерево с оптимальными координатами ТШ для заданной топологии; глобально оптимальным – минимальное ДШ среди всех топологий (МДШ) [1]. Размерность задачи n > 3 определяется числом терминальных вершин дерева. Не нарушая общности подхода, можно рассматривать только деревья с полными топологиями [1], то есть с максимальным числом ТШ, равным n – 2. При оптимизации координат ТШ могут появиться вырожденные дуги (нулевой длины).

Основные допущения модели потоковой задачи – древовидная конфигурация сети и произвольное расположение распределительных узлов (ТШ). Это позволяет применять модель к нашему объекту исследования при условии однородности местности.

Чтобы контролировать падение напряжения у удаленных потребителей, необходимо ввести в модель ограничения:

ным в [4], [5], и подробно остановимся на новом компоненте – блоке адаптации.

AU d < A U, d = 1 + k, k < n , (1) где ∆ U_d – падение напряжения у потребителя d ; k – число потребителей; ∆ U – предельно допустимый уровень падения напряжения.

Целевая функция . Методические рекомендации по оценке эффективности инвестиционных проектов [8] предлагают минимизировать суммарные дисконтированные затраты на строительство и эксплуатацию технического объекта. В распределительной сети такие затраты включают единовременные капитальные вложения

и дисконтированные эксплуатационные затраты в виде стоимости потерь электроэнергии [9]. Соответствующая целевая функция имеет вид:

n

C = V K(sJ +

^{1= 1} к

^T • t n        P

•

E 10 3 • U 2

н

•

si J

• l i ,        (2)

где K ( s_i ) – удельные капитальные вложения, зависящие от сечения провода s_i на дуге i (тыс. руб./ км); τ – тариф на электроэнергию (руб./кВт ∙ ч); t_n – время наибольших потерь мощности (час/ год); E – коэффициент дисконтирования; ρ – удельное сопротивление алюминиевого провода (ом ∙ мм²/км); U_н – номинальное напряжение i (кВА); s_i –

(кВ); S – полная мощность на дуге

сечение алюминиевого провода на дуге i (мм²); l_i – длина дуги i (км).

В формуле (2) выражение в скобках перед l _i – вес дуги i . Весовая функция – квадратичная с разрывами функции от потоков.

Эволюционный алгоритм . Ранее потоковая задача Штейнера использовалась нами для оптимизации транспортных сетей. Были разработаны эволюционная модель [4], генетические операторы [5], композитный алгоритм с направленным поиском [4]. Вычислительный эксперимент, проведенный на тестовых задачах разной размерности, подтвердил эффективность работы алгоритма. Он находит МДШ или хорошие ДШ за конечное число итераций и приемлемое время [3]. Порядок сложности одной итерации – O ( n ³log n ).

На основе этой оригинальной разработки построен эволюционный алгоритм, адаптированный для оптимизации распределительной сети. Он формирует группу альтернативных решений, которые представляют топология, оптимальные координаты ТШ и набор сечений проводов. Блок-схема алгоритма дана на рис. 1.

Для описания алгоритма далее используются известные биологические термины и аналогии. Решение интерпретируется как особь, а его свойства – как фенотип особи. Если справедливы ограничения (1), фенотип особи считается корректным. Мы ограничимся кратким комментарием к компонентам алгоритма, рассмотрен-

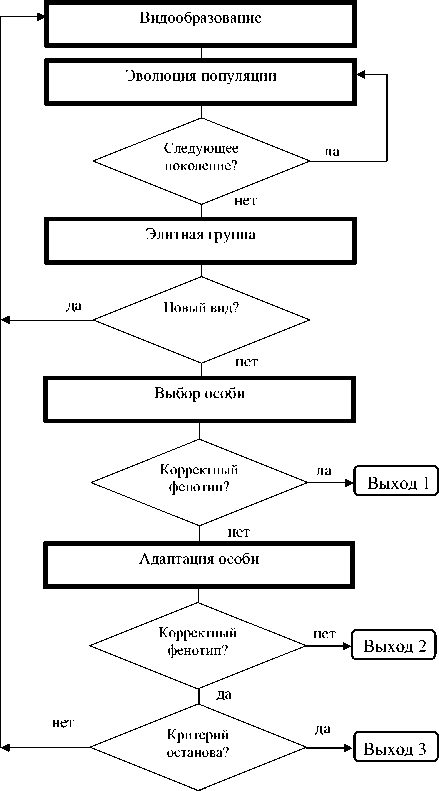
Рис. 1. Обобщенная блок-схема эволюционного алгоритма

Процесс эволюции имитируется на двух взаимосвязанных временных уровнях с помощью генетических операторов. На верхнем уровне происходит случайное образование новых видов особей. Оно начинается со специального предкового вида [5]. На нижнем уровне моделируется эволюция популяции отдельного вида: последовательно генерируются пары популяций – мутантов и гибридных особей [4]. За счет лучших по целевой функции особей создается и обновляется элитная группа. Из нее после завершения поиска выбирается решение.

Если особь имеет корректный фенотип, алгоритм завершается [Выход 1]. Иначе активизируется блок адаптации: ищется особь с корректным фенотипом. Если такой нет, происходит аварийное завершение [Выход 2]. (В этом случае необходим анализ входных данных.)

При работе алгоритма критерий останова может быть отключен. Если он включен, алгоритм ищет ДШ для топологии, полученной до активи-

зации блока адаптации, и завершает работу локально оптимальным решением [Выход 3]. (Это традиционно принятый подход.) Если критерий останова отключен, поиск МДШ продолжается для откорректированной плотности тока. Это позволяет учесть ее влияние на выбор конфигу- рации сети.

Блок адаптации. Сечения проводов на ду- гах сети определяют падения напряжения на них. Назначение блока – найти для сети такой набор сечений, при котором справедливы ограничения (1). Падение напряжения у удаленного потребителя рассчитывается как сумма падений напряжения на дугах пути к нему из источника. (Такой подход корректен, так как при расчете полной мощности предполагается равенство коэффициентов мощности на дугах.) Другой набор сечений определяется процедурой корректировки экономической плотности тока j. Техно- логические ограничения на плотность тока и на множество допустимых сечений гарантируют конечность процедуры.

Блок адаптации реализован в виде цикла по d = 1 * k удаленным потребителям. Одна итера- ция цикла включает следующие шаги.

• 1.    У потребителя d вычисляется падение напряжения по формуле:

  d ΔU d = ∑ i= 1

  
  

• 2.    Если для потребителя d ограничение (1) справедливо, процесс завершается, иначе осуществляется переход к шагу 3.

• 3.    Плотность тока j снижается с заданным шагом Δ j ∈ [0,01; 0,05]. Для каждой дуги i значение сечения s_i , вычисленное по формуле (5), заменяется ближайшим целым из заданного мно-

• жества:

P i ⋅ R i +Q i ⋅ x 0 (s i ) ⋅ l i 10³ U н

где P_i = S_i ∙ cos φ – активная мощность на дуге i (кВт): S _i – полная мощность на дуге i (кВА), φ – угол сдвига между векторами тока и напряжения; R_i – активное сопротивление на дуге i (ом); Q_i = S_i ∙ sin φ – реактивная мощность на дуге i (кВАр); x ₀( s _i) – удельное индуктивное сопротивление для сечения s_i (ом/км); l_i – длина дуги i .

R_i находится по формуле:

R_i = ρ ^{⋅ li} ,                         (4)

si где ρ – удельное сопротивление алюминиевого провода (ом ∙ мм2/км); si – площадь поперечного сечения провода на дуге i (мм2).

s i =      ^Si

н

Корректировка j заканчивается, когда получен набор сечений, для которого ограничение (1) справедливо. Если для какой-то дуги не удается подобрать подходящее сечение, происходит аварийное завершение.

Цикл, выполняемый блоком адаптации, имеет линейный порядок сложности от размерности задачи n . Обычно число итераций цикла, определяемое числом удаленных потребителей, невелико: k <  n . Порядок сложности одной итерации – линейный: порядок шага 2 – O (1), остальных шагов – O ( n ). На шаге 1 в худшем случае, когда путь из источника к удаленному потребителю проходит через n – 2 точки Штейнера, необходимо вычислить n – 3 слагаемых суммы (3). На шаге 3 выполняется конечное число корректировок плотности тока и после каждой определяются сечения на 2 n – 3 дугах [5]. Таким образом, добавление блока адаптации не меняет порядок сложности эволюционной составляющей рассмотренного алгоритма, унаследованной от композитного ЭА [4].

Пример. Работа ЭА демонстрируется на фрагменте реальной сети в Олонецком районе Республики Карелии. Это распределительная сеть напряжением 10 кВ (рис. 2), которая включает подстанцию (точка 1) и 9 потребителей (точки 2–10). Их координаты сняты с карты [10].

Данные для расчетов взяты из ситуационной схемы наружных сетей ОАО «Прионежская сетевая компания» по состоянию на 01.09.2009. Трансформатор понизительной подстанции может регулировать напряжение под нагрузкой в диапазоне ±9 % от номинального напряжения. Предельно допустимый уровень падения напряжения ∆ U = 2 × × 0,09 ∙ 10 = 1,8 кВ, и для удаленного потребителя в точке 10 должно выполняться ∆U ₁₀ ≤ 1,8.

В таблице приведены основные характеристики решений для двух значений плотности тока j . Все обозначения во второй строке таблицы относятся к дуге i. Здесь S_i – полная мощность (кВ); l – длина дуги (км); s – сечение провода (мм²); ∆ ⁱU_i – падение напряже ⁱ ния (кВ); C_i – значение целевой функции (тыс. руб.).

Для расчетов выбрана максимальная экономическая плотность тока j = 1,60 A/мм², принятая в 1960-е годы по «Правилам устройства электроустановок». Характеристики соответствующего решения представлены в левой части таблицы. Так как ограничение ∆ U ₁₀ ≤ 1,8 в нем нарушено, выполнена одна корректировка j с шагом 0,01. Характеристики решения задачи для j = 1,59 A/мм² показаны в правой части таблицы. Оба решения – МДШ, что проверено точным алгоритмом (полным перебором).

Значения целевых функций: 8038,97 = 5447,14 + 2591,83 и 7656,98 = 5641,17 + 2015,82 тыс. руб. соответственно. Первое слагаемое – суммарные капитальные вложения, второе – суммарная дисконтированная стоимость потерь энергии. Улучшение целевой функции произошло за счет существенного снижения стоимости потерь энергии.

Если бы критерий останова был включен, алгоритм завершился нахождением ДШ для топологии, полученной до вхождения в блок адаптации.

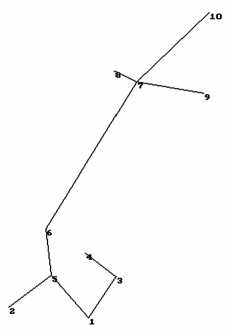
Рис. 2. Существующая распределительная сеть

Зависимость параметров ЛЭП от сечения провода

	j = 1,60					j = 1,59
i	S i	l i	s i	∆U i	C i	S i	l i	s i	∆U i	C i
2	160,00	3,74	16	0,44	531,31	160,00	3,86	16	0,45	548,53
3	400,00	1,67	16	0,37	343,87	400,00	0,00	16	0,28	0,13
4	160,00	0,00	16	0,41	0,10	160,00	1,25	16	0,37	177,86
5	250,00	0,52	16	0,34	82,22	250,00	0,00	16	0,33	0,64
6	100,00	2,64	16	0,57	355,91	100,00	2,75	16	0,39	370,63
7	100,00	0,00	16	1,49	0,16	100,00	0,00	16	1,11	0,10
8	100,00	1,79	16	1,53	241,05	100,00	1,79	16	1,15	240,93
9	160,00	1,31	16	1,68	185,58	160,00	0,74	16	1,21	105,49
10	193,00	5,45	16	1,85	805,34	193,00	5,69	16	1,40	839,60
11	180,00	1,61	16		233,45	762,40	3,00	35		774,40
12	369,00	2,60	16		506,29	317,70	2,67	16		474,24
13	522,40	1,61	25		343,79	369,00	0,82	16		159,99
14	442,40	10,57	16		2354,23	180,00	2,57	16		373,95
15	317,70	3,32	16		590,90	234,00	1,41	16		220,30
16	609,75	2,15	25		522,91	442,40	12,90	25		2453,77
17	909,75	1,24	35		385,12	536,00	3,00	25		653,53
18	1217,00	1,53	50		556,73	1217,25	0,72	50		262,88
Всего:		41,74			8038,97		43,17			7656,98

В этом случае для j = 1,59 A/мм² целевая функция составила бы 7679,95 = 5444,09 + 2235,86 тыс. руб.

Найденные МДШ имеют разные вырожденные дуги, которые появились после оптимизации координат ТШ, и разную суммарную длину сети. Изменились сечения проводов на дугах 11, 13, 17. (Дуги, выходящие из терминальных вершин и из ТШ, имеют номера 2–10 и 11–18 соответственно.) Топологии оптимальных решений также не совпадают, как видно из рис. 3, где штриховой линией показана схема МДШ для j = 1,60, сплошной линией – для j = 1,59.

Общее время решения задачи, включая корректировку и 2 цикла поиска по 5 итераций, составило около 1 мин. на Intel Xeon 5430, 2,66 GHz. Точный алгоритм затратил около 65 мин. на поиск одного МДШ.

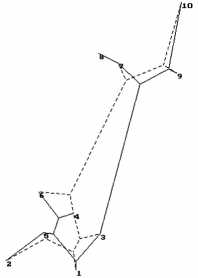
Рис. 3. Сравнение оптимальных топологий

Таким образом, рассмотрено применение модели потоковой задачи Штейнера к воздушным распределительным сетям напряжением 10 кВ. Для решения задачи предложен эволюционный алгоритм, который находит оптимальную конфигурацию сети и набор сечений проводов, удовлетворяющих ограничениям на падение напряжения у удаленных потребителей. Практическая значимость алгоритма показана на примере реальной сети. Алгоритм также можно применять для исследования параметров таких сетей. Дальнейшее развитие алгоритма предполагает учет условий неоднородности местности. Для этого необходима разработка цифровой модели местности.