Эвристическая модель для восстановления рентгеновской части солнечного спектра по спутниковым данным в интересах геофизических приложений

Электромагнитное излучение Солнца является ведущим фактором, создающим ионосферу Земли, которая оказывает сильное влияние на распространение радиоволн [Брюнелли, Намгаладзе, 1988] . Основные процессы, определяющие динамику ионосферы, изучены и описаны, однако данные радиомониторинга говорят о событиях, которые не удается объяснить в рамках известных представлений. К числу таких явлений относятся, например, сбои систем спутниковой навигации, происходящие в условиях, которые в рамках традиционного подхода соответствуют спокойной ионосфере [Afraimovich et al., 2013] .

Одним из путей поиска причин отмеченных событий является создание моделей, позволяющих более строго описать процессы формирования ионосферы и включающих динамику спектров солнечного излучения. Возможность реализации такого подхода связана с наличием данных мониторинга солнечного излучения. Наиболее продолжительный ряд относится к данным, полученным на геостационарных спутниках серии GOES. Данные представляют собой измерения потока излучения Солнца в двух каналах: XL — 0.1–0.8 нм или ~1.5–12.4 кэВ и XS — 0.05–0.4 нм или ~3–25 кэВ (на спутниках GOES-8 –

GOES-12 до 0.3 нм). Сплошные данные, но с разным разрешением, доступны с 1986 г., а отдельные события — с 1974 г. [ data].

С 2002 г. мониторинг ведется на спутнике RHESSI. Его аппаратура содержит твердотельный γ-спектрометр, позволяющий получать спектры в диапазоне от 3–6 кэВ до ~17 МэВ. Существенным недостатком этого спутника является его низкая орбита (~600 км) и соответствующий ей период обращения около 90 мин. Это ограничивает максимальный интервал непрерывного получения данных примерно одним часом для фотонов с энергией более ~10 кэВ и еще меньшим значением в мягком диапазоне, что связано с их поглощением атмосферой Земли. Данные доступны на электронных ресурсах с использованием пакетов HESSI и OSPEX [].

В 2008 г. был запущен низкоорбитальный спутник Fermi, который содержит два основных инструмента: GBM — монитор γ-вспышек с углом обзора 4π в диапазоне 8 кэВ – 30 МэВ и LAT — телескоп в диапазоне 20 МэВ – 300 ГэВ с углом обзора ~20 % неба, предназначенный для исследования жестких γ-вспышек Солнца и солнцеподобных звезд.

Начиная с 2010 г. сбор информации ведется на геостационарном спутнике SDO. В состав его аппа- ратуры входят два спектрометра, работающие на принципах оптической спектрометрии. Данные по спектрам до мая 2014 г. соответствуют интервалу 5.8–106.2 нм, а последующие — интервалу 33– 106.2 нм. Кроме того, имеются фотодиоды для УФ-диапазонов 17.5–21.1 нм (CH18), 23.4–28.1 нм (CH26), 28–32.7 нм (CH30) и рентгена 0.1–7 нм или ~0.18–12.4 кэВ (QD). Последний детектор представляет собой четыре фотодиода c разными направлениями осей, что позволяет определять положение области вспышки на солнечном диске. Выделение всех интервалов производится за счет дифракции. Данные доступны на [ data_access/evewebdataproducts/].

Из сказанного видно, что динамика рентгеновской части (0.1–100 кэВ) солнечного излучения детально представлена интегральными характеристиками, но данные измерений спектра имеются только для области сверхжесткого рентгена 10–100 кэВ (СЖР), причем с большими перерывами по времени. Учитывая, что рентгеновское излучение Солнца играет существенную роль в формировании E- и D-слоев ионосферы Земли, возникает необходимость восстановления его спектра исходя из измеренных интегральных характеристик.

Такая задача была поставлена в работе [Нусинов, Чуланкин, 1997] , где предложен очень простой и удобный в использовании метод приближенного восстановления спектра в диапазоне 0.1–10 нм по измерениям в диапазоне 0.1–0.8 нм (соответствует каналу XL GOES). В основе модели лежит аппроксимационное выражение для интеграла потока энергии фотонов с длиной волны менее λ, полученное путем обработки спутниковых измерений 70–80-х гг. ХХ в. с учетом ряда соображений, касающихся воздействия солнечного излучения на атмосферу Земли. Приведенная в работе формула имеет вид

I _x = C ( X ) I D ^₈, (1)

где C ( X ) = C 0 exp ( - C 1 / C 2 ^{C 2} ) ; D (X) = D ₀ + D 1 /X ; С 0 =73.8; С 1 =3.80; С 2 =0.36; D 0 =0.848; D 1 =0.167; λ — длина волны (нм); I λ , I 0.1–0.8 — искомый и базовый потоки (эрг∙с^–1∙см^–2) (1эрг∙с^–1∙см^–2 = 10^–3 Вт∙м^–2). Отсюда получим очевидное выражение для спектральной плотности мощности

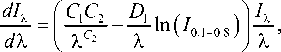
которое далее может быть пересчитано в спектральную плотность потока фотонов.

Между тем опора лишь на один канал измерений и область применимости формул (1), (2) делают невозможным использовать эту модель для исследования событий, которые сопровождаются значительными изменениями показаний в канале XS, но малыми изменениями в канале XL. Анализ таких событий приведен в работе [Корсунская, 2015] .

Восстановление спектра по измерениям на спутниках GOES

В работе [Enell et al., 2008] был использован метод восстановления спектра жесткого рентгена (ЖР) по результатам измерений в каналах XL и XS спут- ников GOES с использованием результатов работы [Garcia, 1994], в которой показано, что по этим измерениям можно восстановить параметры температурного спектра вида

F ( E , T ) = C me E-¹ T ^4/2 exp ( - E/kT ) G ( E , T ), (3)

которым описывается ЖР. В (3) F — спектральная плотность потока (фотон/с/см²/кэВ), E — энергия фотона (кэВ), T — температура (K), k — постоянная Больцмана, G — медленно меняющаяся безразмерная функция, C _ME — размерный множитель, или мера эмиссии, зависящий от количества электронов, участвующих в генерации фотонов, и не зависящий от E и T . Идея подхода состоит в том, что отношение потоков энергии в каналах XL и XS

RXR (T) = J F(E, T)EdE J J F(E, T)EdE (4) XL XS является монотонной функцией T, а следовательно, можно определить обратную функцию TXR(R). Это позволяет по измеренным величинам WXL и WXS вычислить T=TXR(R), где R= WXL/WXS, после чего получить CME.

Авторы работы [Enell et al., 2008] воспользовались видом спектра, предложенным в [Culhane, Acton, 1970] ,

F ( E , T ) =

- 1.3 'y—0.2        I E I I E I

= CE T exp -      1 -       0.33 kT

( kT J(   ( 88.0 )

как результата обработки ракетных и спутниковых экспериментальных данных, полученных в 50–60-е гг. ХХ в. Область применимости (5) обозначена авторами как E = 1.5–15 кэВ и T =4–20 МK. Размерность C не совпадает с размерностью C ME в (3).

Данный подход был реализован в ИДГ РАН Стрелковым при создании модели расчета скорости образования электрон-ионных пар в D- и E-слоях ионосферы во время солнечных вспышек [Ляхов и др., 2015] . Модель как часть более широкой модели была протестирована на экспериментальной базе ИСЗФ СО РАН в КВ-диапазоне и получила хорошую оценку [Ponomarchuk et al., 2015] . Однако верификация по сигналам СДВ-диапазона дала неудовлетворительные результаты, что заставило вернуться к модели спектра.

Для уточнения модели использовался вид спектра, приведенный в [Mewe et al., 1986] . Эта работа является заключительной в серии из шести статей, в которых была рассмотрена задача о спектре излучения электронов с максвелловским распределением энергий в оптически тонкой плазме в нерелятивистском приближении. Задача сводится к получению функции G из (3). В дополнение к подробному описанию ее вида в статье дана упрощенная модель расчета непрерывной компоненты спектра и приведен ее программный код на языке FORTRAN. Именно эта программа использована в нашей работе. Область применимости модели определена авторами как λ= 1÷1000 Ǻ (~12.4 эВ – 12.4 кэВ), T =0.01÷100 МK.

Для спектра Mewe с учетом ширин каналов XL и XS получены функции

J xl ( T ) = J

XL

F ( E , T ) E

dE ,

J xs( T ) = J

XS

R_XL xs (T ) =

XL , XS

c

ME

F ( E , T ) E

ME

J XL( T ) ^:---------------------------------------------------------------------------------------------------------------------------

J XS ( T )

dE ,

и обратная R _{XL, XS} функция T _{XL, XS}( R ). Спектральная плотность потока фотонов определяется согласно (3), где T = T XL, XS ( W XL / W XS ), C ME = W XL / J XL (T), W XL и W XS — измерения спутников GOES.

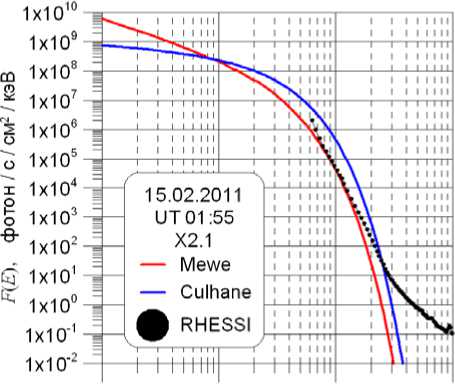
На рис. 1 сопоставлены результаты восстановления спектров с применением приближений Mewe и Culhane, полученные по реальным спутниковым измерениям 15.02.2011 в 01:55 UT (оба спектра продлены за формальные границы области их применимости), а также показан спектр, измеренный на RHESSI. Время соответствует периоду развития вспышки. Поток рентгена относится к классу X2.1.

Видно, что предпочтение должно быть отдано приближению Mewe, которое хорошо согласуется со спектром RHESSI в интервале 7–13 кэВ. Вопрос экстраполяции в область больших значений будет обсужден ниже. Следует также добавить, что спектр в приближении Mewe — один из двух спектров, рассмотренных в работе [Garcia, 1994] .

В связи с тем что приближение Mewe применимо во всей интересующей нас области ниже 10 кэВ, возникает вопрос о достаточности построенного спектра. Для ответа на него был реализован следующий подход. Аналогично функциям J XL и R XL, XS были получены функции J QD ( T ) и R QD, XL ( T ), соответствующие каналу QD спутника SDO. Очевидно, что говорить о достаточности можно тогда, когда величина W XL R QD, XL ( T ), где T = T XL, XS ( W XL / W XS ), близка реально измеренным на SDO значениям.

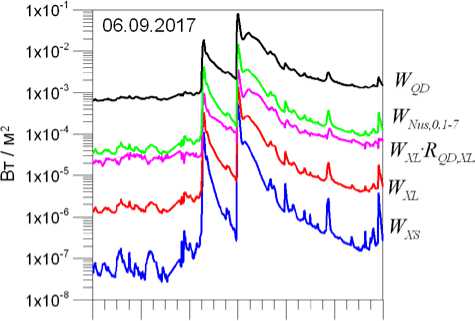
Такой подход был применен к данным, полученным на спутниках GOES и SDO 06.09.2017 во время сильных солнечных вспышек и непосредственно перед ними. Для анализа использованы данные с шагом 1 мин. На рис. 2 показаны результаты спутниковых

0.1           1           10          100

E, кэВ

Рис. 1. Пример восстановленных спектров с использованием приближений Mewe и Culhane, а также спектр, измеренный на спутнике RHESSI измерений для трех рассматриваемых каналов и оценка величины восстановленного спектра в интервале 0.1–7 нм, которая вычислялась для каждого временного интервала. Хорошо видно, что эта кривая лежит существенно ниже кривой WQD и говорить об их близости не приходится.

Приведен также график функции, получающейся в результате применения к измеренным значениям W XL формулы (1) для вычисления интегрального потока в диапазоне 0.1–7 нм. Видно, что эта оценка также сильно (в 5–20 раз) занижает величину потока, а следовательно, формула (2) не может правильно описывать спектр в области мягкого рентгена.

Восстановление спектра по одновременным измерениям на спутниках GOES и SDO

Спектр вида (3) является базой для описания спектра в рентгеновском диапазоне. Это позволило нам применить подход, изложенный выше в отношении каналов XS и XL, к паре XL и QD. Для этого по функции R Q _{D, XL}( T ) получена функция T Q _{D, XL}( R ). Параметры спектра определяются в этом случае как T = T QD, XL ( W QD / W XL ), C ME = R QD, XL ( T ) W XL / J XL ( T ). Будем обозначать этот спектр F Q _{D, XL}( E ), а определенный ранее — F XL, XS ( E ).

На рис. 3 приведены спектры FQD, XL(E) и FXL, X S(E), полученные по реальным измерениям спутников 06.09.2017 в 07:15 (спокойные условия) и 12:01 UT (во время вспышки). Значения температур TXL, XS и TQD, XL для первого из них составляют соответственно 5.03 и 2.19, для второго — 20.79 и 2.93 МK, т. е. в обоих случаях существенно различаются. Помимо рассчитанных спектров, в качестве ориентира показан спектр LASP Reference Spectrum (No. 1 March 25–29, 2008) [ lisird/whi_ref_spectra/].

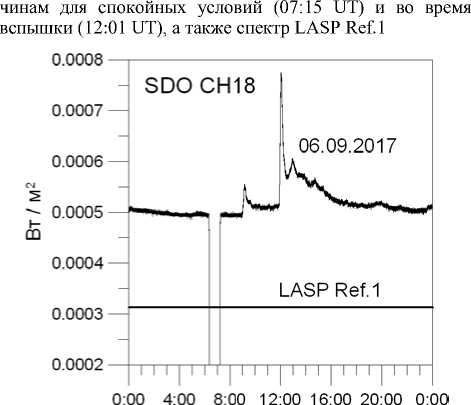
Как сказано выше, приближение Mewe применимо не только в рентгеновском, но и в УФ-диапазоне, показанном на рис. 3. Из этого следует, что поток энергии в каналах УФ-диапазона в 12:01 UT должен быть почти в 100 раз больше их величин в 07:15 UT. Однако, как видно на рис. 4, отношение измерений в канале CH18 (58.7–70.7 эВ) за рассматриваемый день составило ~1.6 (за исключением времени нахож-

0:00 4:00 8:00 12:00 16:00 20:00 0:00 UT

Рис. 2 . Результаты измерений потоков в каналах XS и XL спутников GOES, в канале QD спутника SDO, величина W _XL R Q _{D, XL}, определенная по W _XS и W _XL, а также W _Nus,0.1–7 —оценка потока в диапазоне 0.1–7 нм, полученная по W XL согласно (1)

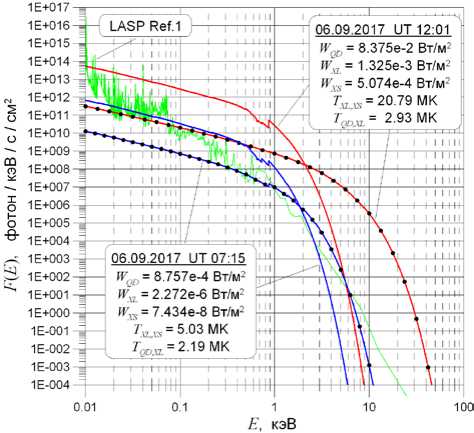
Рис. 3 . Спектры F Q _{D, XL}( E ) (сплошные линии) и F _{XL, XS}( E ) (линии с •) рассчитанные по реально измеренным вели-

ит

Рис. 4 . Результаты измерений в канале CH18 на спутнике SDO за 06.09.2017 и соответствующее ему значение согласно спектру LASP Ref.1

дения спутника в тени Земли), а по сравнению с потоком в канале, соответствующем спектру LASP, не более 2.5. Прямой расчет потока энергии в интервале канала CH18 для спектров F Q _{D, XL} дал значения 8.2·10^–5 Вт/м² для 07:15 UT и 5.9·10^–3 Вт/м² для 12:01 UT. Если первую из этих величин, которая в шесть раз меньше измеренной в это время, можно было бы объяснить использованием нами упрощенной модели спектра, то превышение второй величины в 12 раз над измерениями означает несоответствие модели реальной картине явления.

Использованное нами приближение Mewe является приближением тонкого слоя, т. е. описывает спектр в том случае, если фотоны не поглощаются средой, в которой они родились. Это условие выполняется для той части излучения, которое генерируется в солнечной короне. Однако солнечные вспышки традиционно связывают с солнечными пятнами, т. е. с процессами, развивающимися в самой нижней части атмосферы Солнца — фотосфере. Данное обстоятельство позволило предположить, что область генерации лежит в поглощающем слое, но на такой глубине, с которой жесткая компонента спектра выходит без потерь, в то время как мягкая компонента частично или полностью поглощается средой. При этом поглощение в атмосфере Солнца происходит за счет процессов фотоионизационного взаимодействия с компонентами среды, а родившиеся фотоэлектроны становятся источником более мягкого спектра, расположенного в более высоких слоях. Это означает, что измеряемый спектр может быть представлен в виде суммы спектров нескольких источников.

Исходя из этой концепции и сделав дополнительное априорное предположение, что глубина, на которой происходит генерация спектра, соответствующего температуре T , отвечает оптической толщине τ( kT )=1, мы рассмотрели спектр

F ‘( E , T ) = F ( E , T )exp ( -ct ( E)/ a (kT ) ) , (6) где σ( E ) — среднее сечение поглощения фотонов с энергией E в фотосфере.

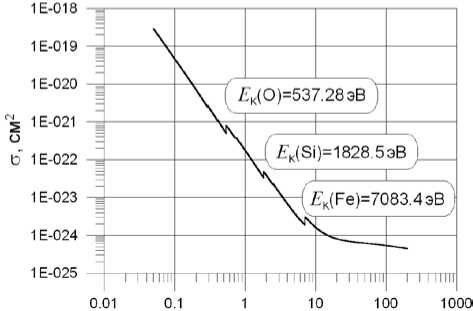
При вычислении сечения принято, что среда состоит из нейтральных атомов в соотношении по числу частиц в единице объема (в %) [Eddy, 1979]: H — 92.0949, He — 7.788, O — 0.06033, C — 0.0303, N — 0.00806, Ne — 0.00752, Fe — 0.00358, Si — 0.00313, Mg — 0.00261, S — 0.00157. Значения сечений атомарных частиц взяты из модели EPDL97 []. График σ(E) для интервала энергий 50 эВ – 200 кэВ приведен на рис. 5. Видны скачки, соответствующие порогам ионизации электронных оболочек, основными из которых являются K-оболочки кислорода, кремния и железа. Между этими энергиями функция считается непрерывной.

С учетом имеющихся данных модельный спектр имеет вид

F Sol ( E ) F XUV ( E ) + F SXR ( E ) + F HXR ( E ). (7)

Полагаем, что спектры F SXR и F HXR связаны с поглощением в атмосфере Солнца, в то время как F XUV соответствует приближению тонкого слоя. Каждый из них характеризуется собственной температурой и мерой эмиссии, которые далее обозначены соответственно T _XUV, T _SXR, T _HXR и C _XUV, C _SXR, C _HXR.

Спектр F _HXR описывает жесткую компоненту. Приведенные выше рассуждения позволяют предположить, что две другие составляющие спектра (7) не вносят вклад в W _XS, поэтому его температура принята равной T HXR = T XL, XS ( W XL / W XS ).

E, кэВ

Рис. 5 . Среднее сечение поглощения фотонов в фотосфере Солнца. Значения порогов ионизации K-оболочек кислорода, кремния и железа

Очевидно, что наличие поглощения меняет вклад источника в спектр излучения, который определяется функциями J ^* XS ( T ), J ^* XL ( T ), J ^* QD ( T ). Эти функции определены для спектра (6) аналогично таковым без символа ^*. Следовательно, для обеспечения требуемого значения в канале XS мера эмиссии для спектра F HXR должна быть увеличена в 1/ K ( T _HXR) раз по сравнению со спектром F _{XL, XS}, где K ( T ) = J XS ( T ) / J XS ( T ). Тогда C HXR = W XL / J XL ( T HXR ) / K ( T HXR ).

Вклад построенного таким образом спектра в канал XL равен W XL, HXR = C HXR J ^* XL ( T HXR ), а в канал QD — W QD, HXR = W XL, HXR R QD, XL ( T HXR ), где R QD, X L ( T ) = = J QD ( T )/ J XL ( T ).

Следует отметить, что с увеличением температуры роль поправки, связанной с каналом XS, увеличивается. На рис. 6 приведены графики доли W _{XL, HXR} в величине W XL с учетом и без учета этой поправки.

Оставшаяся часть потоков в каналах XL и QD должна быть поделена между спектрами F SXR и F _XUV. Имеющихся данных по измерениям в рентгеновском диапазоне недостаточно для того, чтобы получить параметры обоих спектров. Потоки в каналах CH18, CH26, CH30, относящихся к УФ-диапазону, определяются рекомбинационными процессами FeIX и HeII (два канала) [Woods et al., 2012] и относятся к той части спектра, которая не описывается используемым температурным приближением. Поэтому мы приняли, что спектр F XUV в канал QD дает вклад W 0 =2·10^–5 Вт/м², а его температура равна T _XUV=0.7 МK. Мера эмиссии определяется как C _XUV= W ₀/ J Q _D( T _XUV)= W ₀/ R Q _{D, XL}( T _XUV) / J _XL( T _XUV). При этом величина W 0 / R QD, XL ( T XUV ) определяет вклад этого спектра в канал XL.

Для наглядности на рис. 7 приведены все рассматриваемые спектры на основе данных, соответствующих обсуждавшемуся выше случаю 06.09.2017, 12:01 UT. На нем также показан спектр LASP Ref.1. Видно, что спектр F _XUV является «пьедесталом», на котором стоит часть спектра LASP Ref.1 при E < 500 эВ. Выбранное значение W 0 не противоречит результатам измерений. Величина W Q _D, соответствующая спектру LASP Ref.1, равна 1.471·10^–4 Вт/м², а минимальное среднесуточное значение, зарегистрированное на SDO за весь период наблюдений по июнь 2018 г. включительно, не ниже 6·10^–5 Вт/м².

Таким образом, спектр F SXR должен быть построен исходя из того, что его вклады в каналы QD

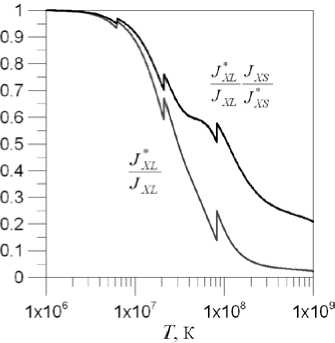
Рис. 6 . Доля W _{XL, HXR} в величине W _XL с учетом и без учета поправки, связанной с каналом XS

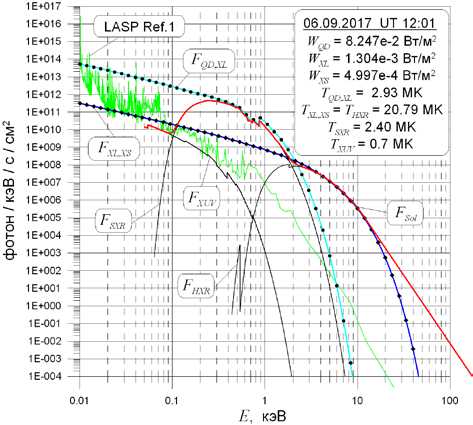
Рис. 7. Пример построения спектров по значениям WXS, WXL и WQD. Спектр FSol построен с применением алгоритма экстраполяции и XL равны WQD, SXR = WQD – WQD, HXR – W0 и WXL, SXR = = WXL – WXL, HXR соответственно. Делать поправку для канала XL за счет спектра FXUV не нужно, так как формальное вычисление этой величины дает 1.25·10–14 Вт/м2, что, по крайней мере, на 5 порядков ниже нижней границы измерений. Для определения температуры построена дополнительная функция T*QD, XL(R), обратная R*QD, XL. Параметры спектра FSXR равны TSXR=T QD, XL(WQD, SXR / WXL, SXR), CSXR= =WXL, SXR/J XL(TSXR).

На рис. 8 приведен суточный ход температур T QD, XL , T SXR и T HXR , вычисленный на основе данных измерений 06.09.2017. Хорошо видно, что на всем интервале времени значения T _SXR меньше T Q _{D, XL}. Следует также отметить, что если диапазон изменений T _SXR составил менее 1.1 МK, то T _HXR менялась в пределах 19 МK.

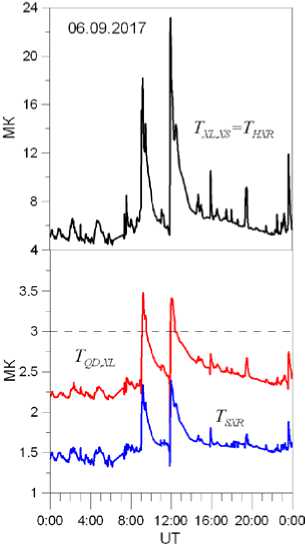
Рис. 8 . Значения температур, полученные по измерениям 06.09.2017

Поведение спектра в диапазоне больших энергий

Как следует из (3) и видно на рис. 7, температурный спектр при E ^ kT экспоненциально падает. Однако, как отмечено еще в обзорной работе [Dennis, 1988] , температурный спектр при больших энергиях переходит в степенной, т. е. ~ E ^–γ. Величина γ меняется в довольно широких пределах, зависит от типа вспышки и фазы ее развития. Для многих вспышек значение γ находится в пределах 7–9, но в некоторых случаях опускается до ~5 и ниже. При этом, как видно на рис. 1, при уходе в еще более жесткую область спектр, оставаясь степенным, описывается функцией с меньшим значением γ.

Из сказанного следует, что при необходимости детального изучения влияния жесткой сверхтемпературной компоненты солнечного излучения на атмосферу Земли необходимо использовать данные спектрометров. В то же время их анализ показал, что в первом приближении можно ограничиться экстраполяцией спектра (7)

F sol ( E )= F Sol ( E 0 )( E / E 0 )^–γ, (8)

где E 0 =6.5 kT HXR ,

_ _ d ln F HXR ^Y d ln E

E > E 0 . Такое

E = E 0

приближение дает показатель степени γ≈ 7.6 ± 0.2. Спектр F Sol , изображенный на рис. 7, демонстрирует данный метод экстраполяции.

Спектр F _Sol не всегда обеспечивает плавное сопряжение с экспериментально полученными спектрами. Для построения единого экспериментальномодельного спектра, который не содержит физически необоснованных скачков, может быть применена следующая модификация описанного метода.

По значению W _XL и экспериментальному спектру, заданному набором точек { ( E data,i , F dat^i )| i = 1, N data } , находится такое значение T ex , что спектр F ( E , T ex ) с C ME = W XL / J XL ( T ex ) достаточно близок F data . Формальный критерий в этом случае имеет вид

)

^{_ 1}

max z

f ^F ( ^E data, i , ^T ex ) F \_           data, i

^e ,

где ε — задаваемая величина. Далее принимается T _HXR≡ T _ex и построение модельной части спектра осуществляется в соответствии с описанной ранее процедурой. Очевидно, что экстраполяция (8) в этом случае не проводится.

Особенности вычислительного алгоритма и экспериментальных данных

Нами была создана программная реализация предложенной модели. Разработанный алгоритм в кратком виде представлен в приложении 1. Для расчета опорных функций, по которым вычисляются параметры спектров, использованы аппроксимации. Их коэффициенты приведены в приложении 2. Коэффициенты аппроксимаций даны с точностью не более шести знаков мантиссы.

Очевидно, что в идеале интегралы j FSol (E)EdE, вычисленные по интервалам, соответствующим ка- налам XS, XL и QD, должны давать исходные значения потоков энергии в них. Расчеты показали следующие относительные ошибки: ±1 % для канала XL, от –2 до +3 % для канала XS, от +1 до +5 % для канала QD. Основной источник этих ошибок с качеством использованных аппроксимационных выражений.

Необходимо отметить, что приведенные величины соответствуют варианту спектра без экстраполяции. Использование экстраполяции влияет только на ошибку в канале XS, которая в этом случае может доходить до нескольких сотен процентов. Такая ситуация возникает тогда, когда экстраполированная часть спектра дает заметный вклад в величину интеграла и наблюдается только в условиях спокойного Солнца.

В общем случае можно утверждать, что чем выше жесткость спектра и больше потоки, тем выше расчетная точность.

Важно отметить еще одну особенность разработанной модели. Использованная нами функция G ( E , T ) не обладает свойствами монотонности и непрерывности ни по одной из переменных, вследствие чего функции R XL, XS ( T ), R QD, XL ( T ) и R^* QD, XL ( T ) также не обладают этими свойствами. В диапазоне, имеющем для рассматриваемой задачи практическое значение, особыми точками являются температуры 1, 1.5, 3, 4.5 и 8 МK. Однако заметный эффект наблюдается только при T = 3 МK, который проявляется в невозможности в окрестности этой точки определить функции T _{XL, XS}( R ) и T^* Q _{D, XL}( R ) как обратные и необходимости их достраивания с помощью дополнительных соображений. В то же время температура жесткой компоненты спектра ~3 МK соответствует спокойному Солнцу, т. е. ситуации, когда вид спектра в значительной мере определяется принятой моделью экстраполяции. Для мягкой компоненты это значение слишком высоко и не было достигнуто ни в одном рассмотренном случае. Таким образом, некоторый волюнтаризм в определении этих функций не сказывается на конечном результате.

Отличие созданной реализации от описанной теоретической модели состоит в том, что, как показала практика, учет поправки J ^*_XS/ J _XS при малых значениях T HXR дает бóльшую ошибку интеграла потока энергии по сравнению с вариантом, когда эта поправка не делалась. Поэтому было решено принять K ( T )=1 при kT < E K (O), т. е. доля W XL, HXR в величине W _XL, изображенная на рис. 6, для температур, лежащих левее левого скачка функций, соответствует не верхней, а нижней кривой.

Как сказано выше, экспериментальные данные со спутников GOES соответствуют двум вариантам определения диапазона XS (0.05–0.4 и 0.05–0.3 нм), поэтому опорные функции T XL, XS ( R ) и K ( T ), зависящие от ширины канала, представлены в приложении 2 для обоих вариантов. Однако основной объем экспериментального материала со спутника SDO приходится на период функционирования спутников GOES с аппаратурой, соответствующей диапазону 0.05–0.4 нм, поэтому все приводимые в настоящей работе результаты относятся к этому случаю.

Важно также помнить, что, согласно [GOES_XRS_readme], для получения реальных значений потоков архивные данные со спутников с но- мерами 8–15 необходимо перемасштабировать, разделив считанное значение канала XL на 0.7, а канала XS — на 0.85.

В большинстве случаев на один и тот же период времени приходится работа двух или более спутников GOES. Это позволяет получать непрерывный ряд экспериментальных данных даже тогда, когда один из спутников находился в тени Земли или был выведен на профилактику. Однако одновременные измерения разных спутников различаются. Наибольшие расхождения наблюдаются в период низкой солнечной активности. Анализ данных показал, что в качестве основных следует принимать измерения GOES-15. Нижняя граница архивных значений канала XS₁₃ (нижний индекс — номер спутника) равна 2·10^–8 Вт/м², поэтому отличие от XS₁₅ может доходить до 20 раз. Данные XL₁₄ и XS 14 не рекомендуется использовать, если они лежат ниже 10^–7 Вт/м². Анализ данных спутников 8–12 не проводился.

При использовании спутниковых данных следует помнить, что измерения GOES приведены к орбите Земли, в то время как почти все материалы с SDO и все данные спутников RHESSI и Fermi отнесены к 1 AU. Среднесуточные коэффициенты пересчета на 1 AU (квадрат расстояния от Солнца до Земли в AU) содержатся в архиве GOES. Однако связанная с этим поправка не выходит за пределы ±3.4 %, поэтому ее учет скорее всего можно считать избыточным для задач геофизики.

При построении экспериментально-модельного спектра не имеет смысла рассматривать экспериментальные точки далее ~30 кэВ, а также следует ограничиться той частью, которая соответствует области монотонного спада.

Обсуждение результатов

Для оценки качества предложенной модели было проведено сравнение модельных спектров F Sol , полученных на основе результатов реальных измерений, со спектрами RHESSI, а также с модельными спектрами F _Nus, рассчитанными по формулам (1), (2) для тех же исходных данных, в интервале энергий фотонов 0.124–12.4 кэВ.

На рис. 9 представлены спектры, соответствующие потокам X2.1, M3.2, M2.4 и C1.2 классов. Видно, что в двух первых случаях спектр F _Sol хорошо согласуется со спектром RHESSI. Модельные спектры для энергий более ~1.5 кэВ совпадают или очень близки.

В ситуации, показанной на рис. 9, в , модельный спектр лежит несколько ниже экспериментального, а экстраполяция дает бóльшую скорость спада по сравнению с реальной. Причина может заключаться в том, что, как отмечено в [Dennis et al., 2006] , в ряде случаев низкоэнергетичная часть спектра RHESSI соответствует мультитемпературному приближению. Очевидно, в такой ситуации использованного нами приближения (7) недостаточно для корректного

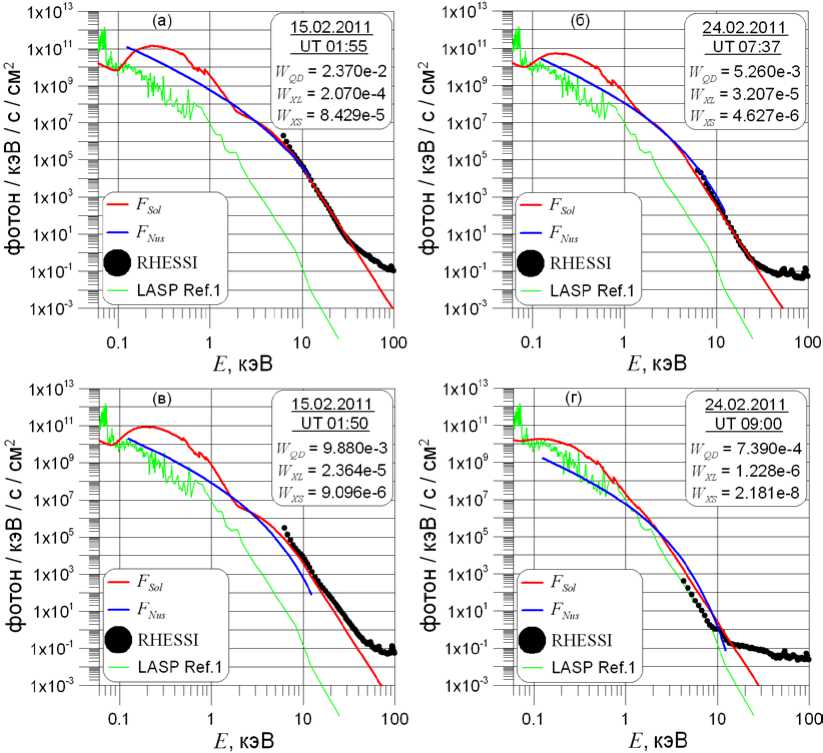
Рис. 9 . Сравнение модельных спектров F _Sol и F _Nus с экспериментальными данными

описания спектра. Модельный спектр F Nus лежит еще ниже спектра F _Sol.

Спектр F _Sol, показанный на рис. 9, г , в диапазоне ЖР лежит немного выше спектра RHESSI, однако скорость его спада близка к экспериментальным значениям. Он также близок к жесткой части спектра F _Nus, но лучше описывает спад.

Анализ спектров показывает, что чем ниже класс потока, тем хуже модельный спектр согласуется с экспериментальным. Вероятно, это связано с особенностями аппаратуры спутников GOES и моделью пересчета результатов измерений в потоки энергии. Ширины каналов XL и XS, обозначаемые как 0.1– 0.8 и 0.05–0.4 нм, являются лишь некоторыми эффективными значениями. Реальные окна пропускания, рассчитанные для GOES-13 и приведенные в [GOES_XRS_readme], определены как 0.02–1.6 и 0.01– 0.8 нм соответственно. Это означает, что в ситуации, когда температурная часть спектра Солнца сравнительно мала, повышение потоков в СЖР-диапазоне может значимо сказываться на измеряемой величине. Пример такого спектра приведен на рис. 10, а .

На рис. 10, б продемонстрирована еще одна проблема, с которой мы столкнулись. Как следует из указанных на графике значений, потоки в каналах XS, XL и QD на 16.02.2018 были значительно ниже потоков на 12.09.2017. Поведение модельных спектров FSol полностью им соответствует. Однако спектр RHESSI для 16.02.2018 в диапазоне энергий менее ~20 кэВ лежит значительно выше его спектра для 12.09.2017. Это различие доходит до двух по- рядков. Таким образом, видна явная несогласованность результатов измерений разных спутников. Причина этого нам не известна, но можно предположить, что она связана с начавшимися проблемами с детекторами спутника RHESSI, которые 11.04.2018 были отключены из-за перегрева.

Как видно на рис. 9 и 10, а , в области мягкого рентгена спектр F _Nus лежит значительно ниже спектра F Sol . Это полностью согласуется со сделанным ранее утверждением, что значение потока в диапазоне, эквивалентном ширине канала QD, вычисленное по формуле (1), оказывается существенно меньше реальных измерений. Поэтому для проверки предлагаемой модели был применен следующий подход. Учитывая, что модель оставляет широкий произвол задания входных значений потоков в трех каналах, были рассмотрены случаи, когда входным параметром является W _XL, а W Q _D и W _XS вычисляются с использованием формулы (1).

На рис. 11 показаны два варианта таких расчетов. Они соответствуют спектрам на рис. 9, в , г , для которых было получено наибольшее расхождение двух модельных спектров. Значения потоков W _XL, указанные на графиках, являются скорректированными значениями, а W QD и W XS — вычисленными по формуле (1). Спектры F _Nus и F _Sol на рис. 11, а фактически совпадают при энергиях более 0.23 кэВ, а для варианта на рис. 11, б заметное расхождение получается только выше ~8 кэВ.

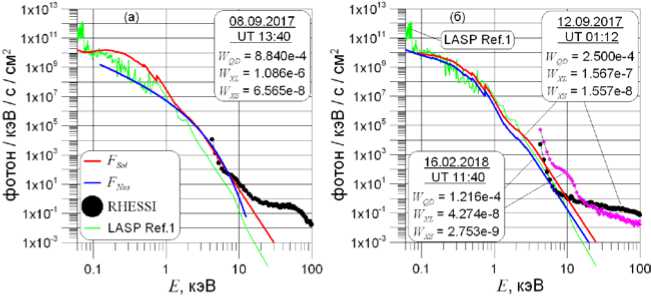
Рис. 10 . Аналогично рис. 9, но для класса C1.1 при повышенном потоке в СЖР диапазоне ( а ); б — спектры F _Sol и RHESSI для двух моментов времени, демонстрирующих рассогласованность данных разных спутников. W _XS и W _XL — нескорректированные значения. Единицы измерения — Вт/м²

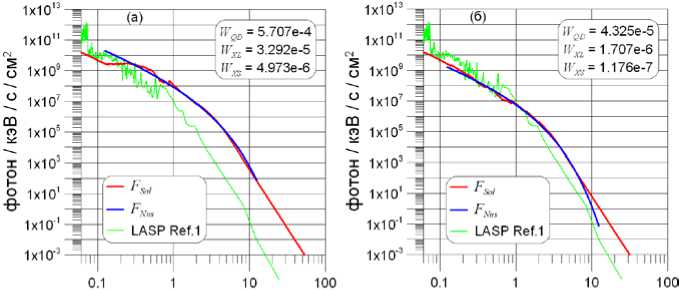
Е, кэВ                                   Е, кэВ

Рис. 11 . Сравнение спектра F _Nus и спектра F _Sol, построенного по значениям потоков W Q _D и W _XS, вычисленным по формуле (1) согласно W _XL. Панели а , б соответствуют рис. 9, в , г . W _XL — скорректированное значение. Единицы измерения — Вт/м²

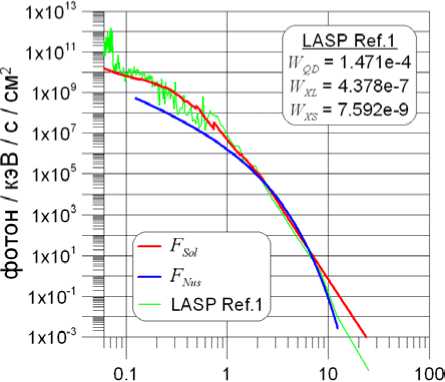
Завершая обсуждение, сравним спектр LASP Ref.1 с модельными спектрами F _Nus и F _Sol, которые получены по интегральным характеристикам потоков, рассчитанным непосредственно по исходному спектру. Их величины, а также сами спектры приведены на рис. 12. Видно, что спектр F Sol в диапазоне мягкого рентгена ближе к исходному спектру, чем F Nus , а в интервале 2–8 кэВ все три спектра почти совпадают. Превышение спектра F _Sol над LASP Ref.1 в более жесткой части не имеет значения, поскольку, как видно на рис. 10, даже при маленьких потоках в каналах XL и XS спектры RHESSI лежат выше спектра LASP Ref.1.

Суммируя сказанное, можно утверждать, что предложенная модель восстановления спектра солнечного излучения дает результаты, хорошо согласующиеся с экспериментальными и теоретическими спектрами в области их совместного применения. Вычислительная ошибка, определяемая точностью задания опорных функций, необходимых для расчета параметров модельного спектра, не оказывает существенного влияния на конечный результат.

Применение модели к реальным спутниковым данным дает спектры, которые не содержат значимой составляющей в диапазоне УФ-излучения, следовательно, нижней границей модельных спектров, построенных по полной модели, является граница рентгеновского диапазона 100 эВ. В отсутствие данных SDO возможно построение спектра для энергий фотонов более 1.5–2 кэВ.

Верхняя граница применения модельного спектра определяется значением спектральной плотности потока фотонов. Сравнение его со спектрами RHESSI показало, что эта граница может быть установлена на уровне 10^–2 фотон/кэВ/с/см². Значение энергии, соответствующее такому потоку, варьирует в пределах от 10 до 100 кэВ. Для детального изучения воздействия жесткой компоненты спектра солнечного излучения на атмосферу Земли необходимо рассматривать экспериментально-модельный спектр, метод построения которого также изложен в настоящей работе.

Е, кэВ

Рис. 12 . Спектр LASP Ref.1 и модельные спектры F _nus и F _sol, полученные на основе интегральных характеристик, вычисленных по исходному спектру

Представленный подход построения спектра по данным спутниковых измерений оставляет возможность его уточнения, один из способов которого сводится к определению параметров компоненты F _XUV по реальным измерениям в УФ-диапазоне.

К сказанному следует добавить, что, по своей сути, разработанная модель является вариантом построения мультитемпературного спектра.

Все спутниковые экспериментальные данные, использованные в работе, взяты из электронных ресурсов в период январь–май 2018 г.

ЗАКЛЮЧЕНИЕ

В работе изложены общие принципы построения рентгеновской компоненты спектра Солнца по данным измерений в каналах XS и XL спутников GOES и QD спутника SDO в рамках мультитемпературного приближения, опирающегося на температурный спектр в приближении Mewe [Mewe et al., 1986] . Сопоставление модельного спектра с данными измерений спутника RHESSI позволило определить границу перехода температурного спектра в степенной.

Описание алгоритма и аппроксимационные выражения опорных функций для вычисления параметров спектра приведены в Приложении.

В период подготовки статьи стало известно, что после 16 лет работы вместо запланированных двух спутник RHESSI прекратил свое существование как научный прибор.

Работа выполнена в рамках гос. задания № 01462019-0010.