Эвристические алгоритмы поиска маршрутов передачи данных в спутниковых системах и их валидация

Компании Boeing, SpaceX, Telesat и другие в ближайшие годы планируют создать спутниковые системы, предназначенные для передачи интернет-трафика, которые будут насчитывать тысячи спутников [1]. С учетом огромного количества, спутников в системе передача, данных между двумя фиксированными точками в ней возможна, с задействованием различных цепочек, которые отличаются временем передачи данных, энергетическими затратами и другими параметрами. При этом перед разработчиками системы возникает задача, построения таких алгоритмов формирования маршрутов передачи данных, которые максимально соответствуют заданным критериям эффективности.

Решение этой задачи, основанное на. простом переборе всех возможных маршрутов, имеет крупный недостаток — факториальную зависимость объема, выходных данных и соответственно времени работы программы от количества спутников в системе. В этом случае генерируется избыточное количество маршрутов, отличающихся перестановками подпоследовательностей. Даже в системах, насчитывающих около 20 спутников, количество

«Московский физико-технический институт (национальный исследовательский университет)», 2020

маршрутов передачи данных, формируемых при простом переборе, достигает нескольких десятков миллионов. В связи с этим в настоящей работе рассматриваются модели и алгоритмы формирования маршрутов передачи данных в спутниковых системах, основанные на некоторых эвристиках, позволяющих значительно снизить затраты времени на проведение расчетов и объем выходных данных, а также методы валидации программ, реализующих эти алгоритмы.

2.    Эвристические алгоритмы поиска маршрутов

В рамках настоящей работы положение спутников в системе в каждый фиксированный момент времени, для которого необходимо построить маршруты передачи данных, описывается взвешенным графом, вершины которого представляют отдельные спутники, положение которых в пространстве задано фиксированными на этот момент времени координатами, а ребра характеризуют возможность передачи данных между парой спутников, принадлежащих ребру. Вес ребра — расстояние между соответствующими спутниками.

На этом графе выделяется пара спутников (наачальный и конечный), для которой необходимо найти «квазиоптимальные» маршруты передачи данных. При этом критерии «квазиоптимальности» описываются, исходя из некоторых эвристических соображений, представленных ниже.

2.1.    Ограничение поиска до трёх маршрутов на пару

Первая модель сокращения количества маршрутов заключается в поиске конкретно описанных маршрутов между двумя вершинами графа, каждой из которых соответствует спутник. Отдельно набираются маршруты для каждой пары спутников, один из которых — начальный.

Формируется пара начальный спутник - конечный спутник (конечный спутник — любой спутник группировки, в том числе начальный), для которой запускаются три этапа поиска. Формируется множество маршрутов Routes, изначально заданное как пустое. На каждом этапе в Routes добавляется один маршрут, если он ещё не был добавлен (в таком случае на соответствующем этапе ни один маршрут не добавляется).

Этапы поиска маршрутов:

• 1)    Нахождение кратчайшего по расстоянию маршрута.

Для поиска кратчайших маршрутов во взвешенном графе используется алгоритм Флойда-Уоршелла [2].

В рамках данного алгоритма находятся кратчайшие расстояния между всеми вершинами графа. Выбор пал на него в силу особенностей третьего этапа поиска. В общем случае для первого и второго этапов может использоваться Алгоритм Дейкстры [3] как алгоритм с лучшей, в сравнении с Флойдом-Уоршеллом, сложностью [4].

Алгоритм заключается в поэтапном прохождении по всем вершинам. Определяется число d^j — длина кратчайше го пути от вершины г до вершины j, который помимо вершин г и j, проходит только через вершины 1... к, где все вершины пронумерованы, г, j и к — номера вершин, а всего вершин п. Таким образом, d0 — длина ребра между г и j (если его нет, длин а обозначается как то), a d^ — длина кратчайшего пути между г и j. Алгоритм также позволяет построить матрицу следующих вершин Next; п^ = к означает, что в кратчайшем пути между г и j следующая за г вершина — к.

Если для рассматриваемой пары (s, t), г де s — номер начального спутника, t — номер конечного спутника, d^_t = то, по матрице Next восстанавливается путь из вершины s в вершину t. который добавляется в Routes.

• 2)    Нахождение маршрута с минимальным количеством промежуточных вершин.

На втором этапе для нахождения кратчайших по количеству промежуточных спутников маршрутов все расстояния в графе заменяются на единицы. Таким образом, если между вершинами было ребро, её вес вместо расстояния между вершинами теперь равен единице. Соответственно, минимизация количества промежуточных вершин эквивалентна минимизации количества рёбер.

Если полученный на данном этапе маршрут совпадает с полученным на предыдущем этапе, добавление Routes не происходит.

• 3)    Нахождение маршрута, наиболее непохожего на найденный на первом этапе маршрут.

2.2.    Поиск маршрутов по извилистости 2.3.    Поиск набора альтернативных маршрутов

Непохожие маршруты ищутся следующим образом. В начале маршрут состоит только из одного спутника — начального. Затем берётся спутник, который должен быть добавлен следующим в маршрут в соответствии с поиском кратчайшего по расстоянию маршрута. Вместо этого спутника в маршрут добавляется самый удалённый (по расстоянию) от него спутник. На этом моменте используется матрица следующих вершин Next, полученная на первом этапе. Если из самого удалённого нет пути до конечного спутника, берётся следующий по удалённости и так далее. В конечном счёте, если ни из какого другого спутника нет маршрута до конечного спутника, берётся сам спутник. Далее алгоритм повторяется для добавленного спутника. Этап завершится, когда конечный спутник будет добавлен в маршрут.

Данная модель предназначена для фильтрации маршрутов, генерируемых при полном переборе. Новый спутник не добавляются в маршрут на очередном шаге алгоритма, если направление на него слишком сильно отклоняется от того направления, которое сформировалось на предыдущем шаге.

Другими словами, при добавлении в маршрут, состоящий из хотя бы двух спутников, очередного спутника рассматривается условие извилистости. Формулируется оно следующим образом:

| cos(a)| <7.                                            (1)

В свою очередь cos(a) вычисляется через скалярное произведение как угол между двумя рёбрами: существующий отрезок маршрута и рассматриваемый отрезок между двумя спутниками.

Параметр 7 является входным параметром модели. При 7 = 1 оставляются все маршруты, а при 7 = 0 — только маршруты, накладываемые на прямые линии. В рамках экспериментов было выяснено, что наилучшие результаты (в плане сокращения количества маршрутов) достигаются на 7 ~ 0,1.

Модель поиска набора альтернативных маршрутов основана на требовании гарантированного обеспечения бесперебойной связи между начальным и конечным спутником. Алгоритм формирует запасные маршруты, задействующие по возможности другие спутники.

Для каждой пары начальный спутник-конечный спутник создаётся копия графа с весами 1 на. рёбрах.

Производится некоторое количество итераций:

• 1)    Нахождение кратчайшего пути от начального до конечного спутника во взвешенном графе с помощью алгоритма Дейкстры.

• 2)    Увеличение веса всех рёбер, инцидентных всем вершинам найденного маршрута. При этом для рёбер в маршруте увеличение веса происходит дважды (по одному разу для каждой инцидентной вершины).

• 3)    Если найденный кратчайший путв уже содержится в списке найденных маршрутов, то увеличиваем счетчик количества неудачных попыток - при превышении порогового значения прекращаем итерации (выходим из цикла). Если найденный кратчайший путв не содержится в списке найденных маршрутов, то добавляем его в список и сбрасываем счетчик количества неудачных попыток.

3.    Подходы к оценке корректности работы алгоритмов поиска маршрутов 3.1.    Проверка сходства близких по временным рамкам решений

Ограничения на количество подряд идущих неудачных попыток нахождения нового маршрута, как и ограничение на суммарное количество попыток, позволяют контролли-ровать количество формируемых моделью запасных маршрутов и время выполнения программы.

Поиск маршрутов передачи данных в системе, состоящей из большого числа спутников, является задачей комбинаторного типа. Тестовые данные для проверки такого типа задач в полном объеме практически всегда отсутствуют. В этом случае для проверки модели приходится применять качественные методы, предусматривающие формулировку некоторых свойств, которые должны соблюдаться в выходных данных при целенаправленном изменении входных параметров. Эти свойства могут быть сформулированы, исходя из особенностей задачи. При этом факт соблюдения этих свойств является необходимым, но недостаточным условием для принятия решения о корректности модели.

Одним из свойств рассматриваемой задачи является кусочное постоянство решения. Действительно, множество существующих маршрутов формируется на основе графа прямой видимости. Граф прямой видимости, в свою очередь, меняется в определённые моменты времени - когда один спутник перестаёт видеть другой. Это значит, что на временных промежутках между моментами изменения видимости граф постоянен. Следовательно, на этих временных интервалах не меняется множество найденных маршрутов.

Для проверки постоянства графа зададим метрику сходства двух графов. Сопоставим каждому графу матрицу смежности. Для определения сходства матриц смежности предлагается использовать меру Жаккара (2). Мощностью матрицы будем считать сумму значений всех ячеек. Поскольку в ячейке могут быть значения только 0 или 1, фактически мощность матрицы будет равна удвоенному количеству неориентированных рёбер. Пересечением двух матриц будем считать матрицу, полученную с помощью попарного произведения ячеек. Объединение двух матриц будем производить с помощью функции максимума, применяемой к парам ячеек:

₌ I- ^{4 и B}I

^{J (А,В} )   |Аn BI ■                                    ⁽²⁾

Результат проверки сходства графа, построенного для 50 спутников в 1000 моментов времени, изображен на рис. 1.

Проанализируем полученные результаты и оценим погрешность метрики.

Спутники в среднем совершают оборот за 100 итераций - 1/100 полного угла за итерацию. Если спутники распределены равномерно по окружности, то сектор между соседними спутниками 1/50 = 2/100 полного угла. В среднем каждый спутник каждые две итерации теряет из виду один спутник и начинает видеть другой спутник. Это означает, что в матрице смежности каждые две итерации изменяется в среднем 100 ячеек, соответственно 50 ячеек каждую итерацию.

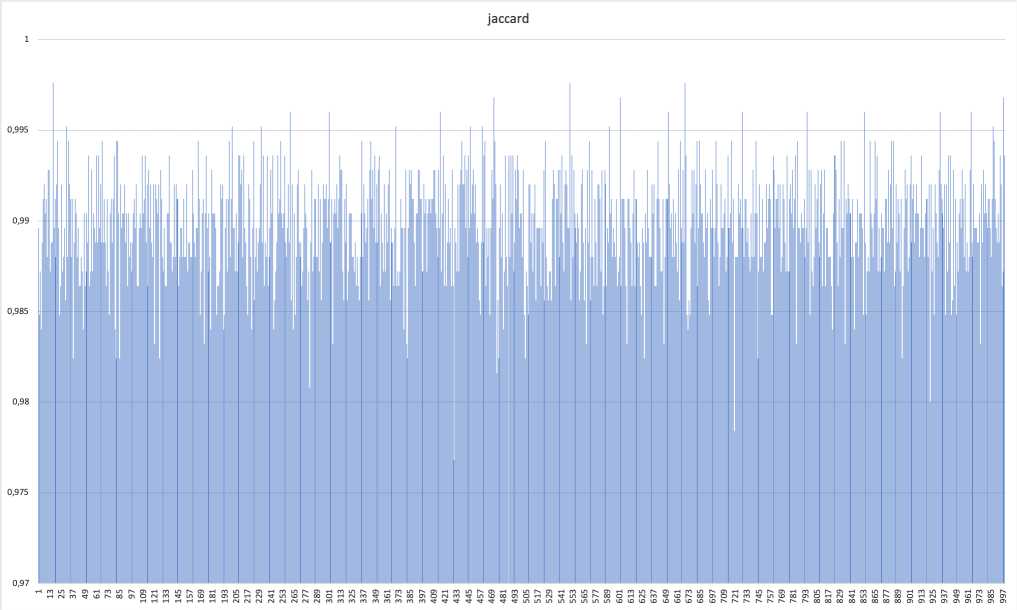
Рис. 1. Метрика Жаккара, 50 спутников, 1000 итераций

В матрице смежности для этого случая всего 50 • 50 = 2500 ячеек. Тогда погрешность метрики имеет порядок е « 50/2500 = 0,02. Если округлить значения выше 0,985 до 1, получим кусочно-постоянную функцию (см. рис. 2).

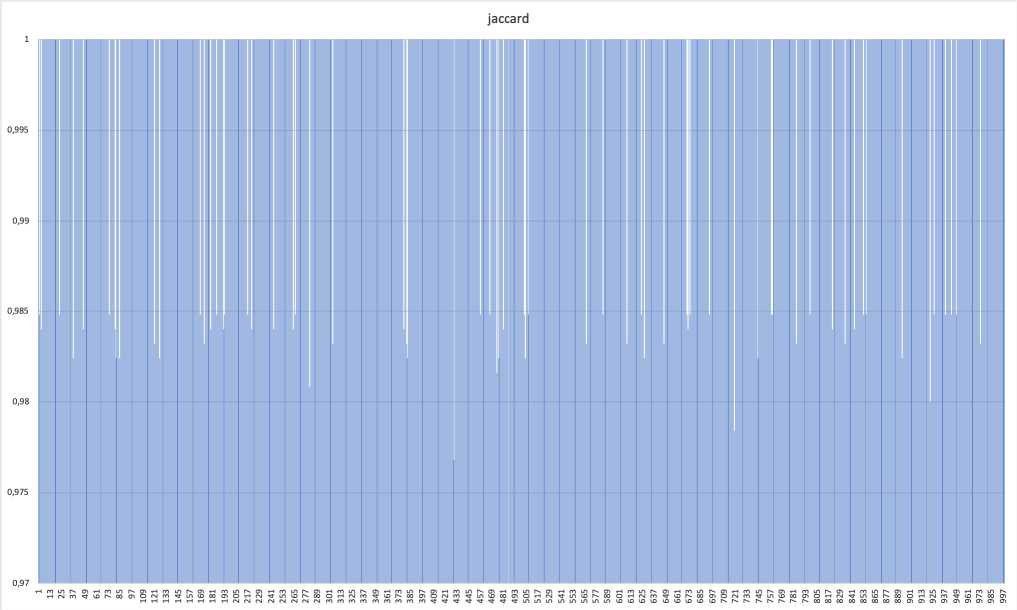
Рис. 2. Метрика Жаккара, 50 спутников, 1000 итераций; значения выше 0,985 округлены до 1

Мы видим, что с учётом полученной погрешности метрика на последовательном наборе итераций имеет вид кусочно-постоянной функции. Значит, текущая реализация алгоритма удовлетворяет заданному показателю корректности - решения в близкие моменты времени имеют практически полное сходство.

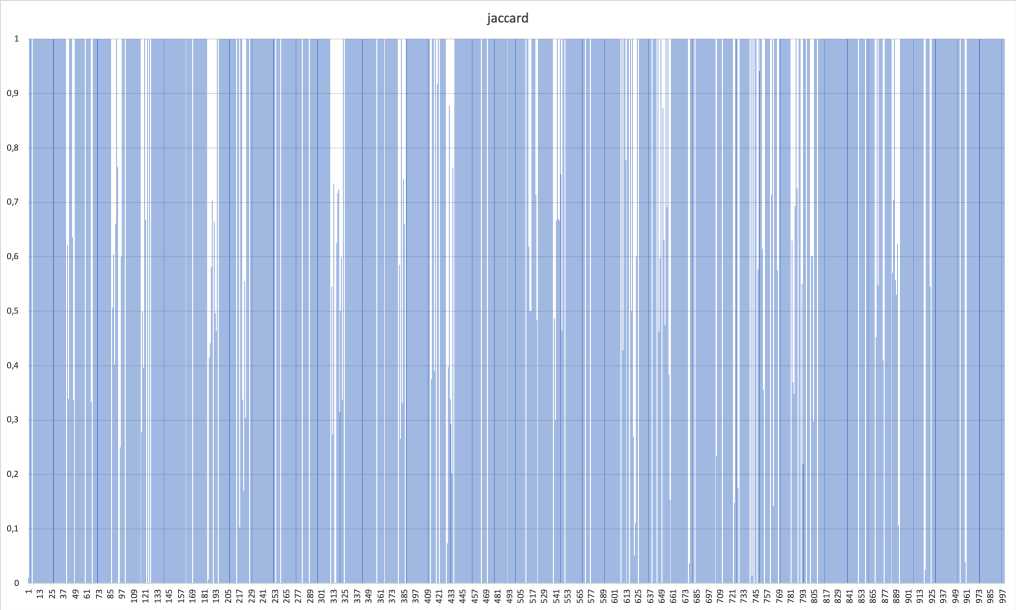
Рис. 3. Метрика Жаккара, 20 спутников, 1000 итераций, поиск всех

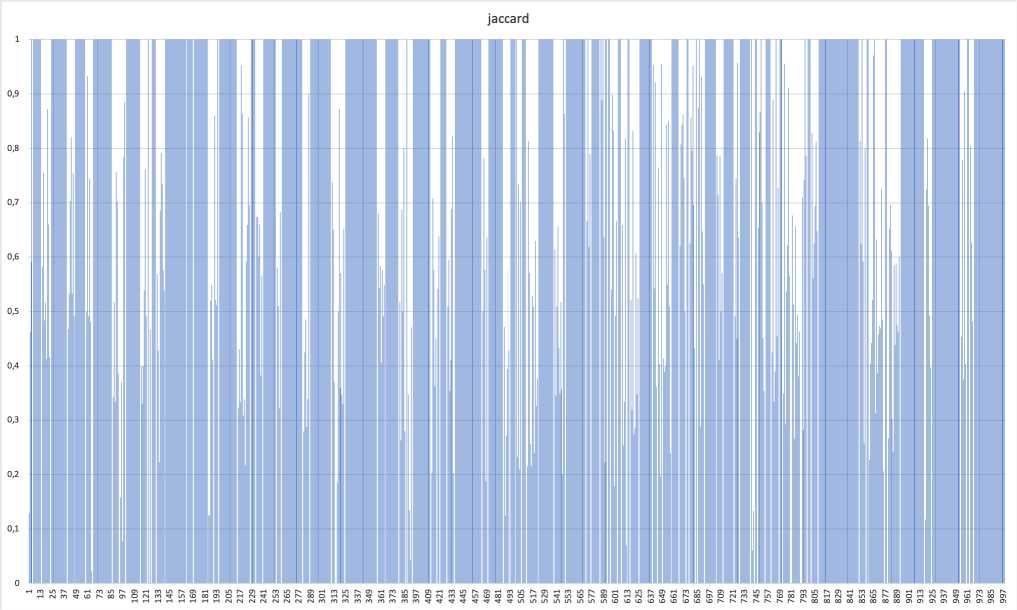
Рис. 4. Метрика Жаккара, 20 спутников, 1000 итераций, ограниченный поиск в три этапа

Схожесть графов в смежных моментах времени позволяет выдвинуть предположение о схожести множества маршрутов в смежных моментах времени.

Это значит, что для соседних промежутков времени маршруты не должны сильно отличаться друг от друга. В рамках данной работы был проведён ряд экспериментов для трёх моделей поиска маршрутов передачи данных: поиск всех маршрутов, ограниченный поиск в три этапа и поиск с учётом извилистости.

Вычислялась метрика Жаккарда для двух множеств маршрутов, полученных в результате поиска для двух соседних промежутков времени. Каждый эксперимент ставился на одном и том же наборе спутников (в количестве 20) и на одних и тех же смежных моментах времени (в количестве 1000).

Результаты приведены для полного перебора (рис. 3) и для каждой описанной модели

(рис. 4-6).

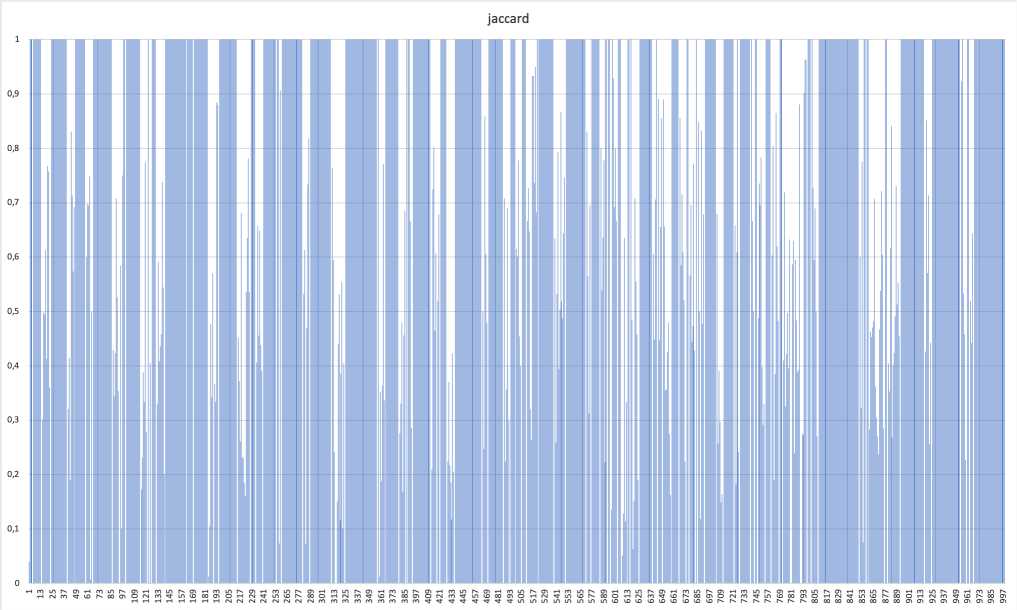
Рис. 5. Метрика Жаккара, 20 спутников, 1000 итераций, поиск с учётом извилистости

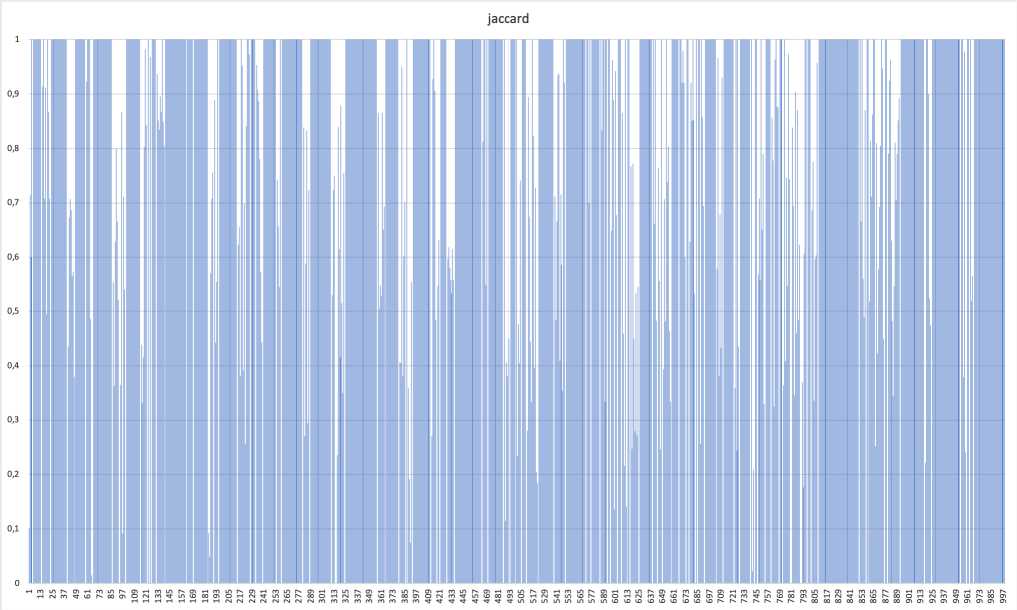
Рис. 6. Метрика Жаккара, 20 спутников, 1000 итераций, поиск набора альтернативных маршрутов

На рис. 3 6 есть периоды кусочного постоянства. Они наблюдаются даже для эвристических моделей поиска маршрутов, которые по замыслу выдают неполный набор маршрутов.

3.2.    Проверка инвариантности результатов вычислений в зависимости от системы координат

Ещё одним свойством задачи является инвариантность решений по отношению к используемой системе координат. В самом деле, поскольку необходимо найти маршруты от одного спутника до другого, представление их положения в той или иной системе координат не должно сказываться на результате. Ведь взаимное расположение спутников не меняется при переводе из одной системы координат в другую, а поиск всевозможных маршрутов должен выдавать один и тот же результат, отличающийся разве что порядком маршрутов друг относительно друга, в любой системе координат.

Рассматриваются две системы координат:

• 1)    Инерциальная (далее — ИСК)

• 2)    Вращающаяся (далее — ВСК)

4.    Заключение

В ИСК меняются координаты только у спутников, тогда как Земля остаётся неподвижной. В ВСК неподвижна только ось вращения Земли, то есть координаты меняются не только у спутников, но и у наземных станций.

Соответственно, при правильной работе алгоритма результаты должны совпадать (в частности, метрика Жаккара тождественно равна 1). При том, что в работе в разных системах координат каждому спутнику соответствуют разные числовые значения координат. Получается, что на разных входных данных должен выдаваться один и тот же результат. Это условие справедливо не для всех стратегий, а для стратегий, зависящих от взаимного расположения спутников. В частности, проверка условия выполнялась для стратегий, описанных в параграфах 2.1 и 2.2 данной статьи.

Сравнение результатов работы алгоритма на одних и тех же наборах спутников, но в разных системах координат может служить косвенной проверкой корректности.

В частности, если в реализации третьего этапа стратегии ограничения до трёх маршрутов на пару (2.1) не учитывать наличие существования пути между спутниками, в множество Routes могут добавляться несуществующие маршруты, которые, более того, различаются в зависимости от системы координат ввиду различных численных значений координат спутников. В рамках эксперимента было проведено сравнение маршрутов на выходе по метрике Жаккара с учётом данной корректировки. В результате значение метрики перестало быть равным единице во всех случаях запуска (впрочем, могут быть такие входные данные, на которых значение останется равным 1, например, если все спутники находятся в зоне видимости друг друга). Было проведено 10 тестов, минимальное значение метрики Жаккара было 0,48. максимальное — 0, 73.

В работе представлен ряд эвристических моделей маршрутизации связи в спутниковых системах и методики их валидации, с помощью которых были проверены необходимые, но недостаточные, условия правильности моделей. Разработка представленных моделей является первым шагом к построению более сложных моделей поиска маршрутов, основанных в свою очередь на более сложных метриках и с большим количеством ограничений. В последующем имеет смысл учитывать ограничение на количество каналов связи, которые спутник может поддерживать, скорость передачи данных, объемы запоминающих устройств, а также динамические параметры системы управления спутником.