Эвристический алгоритм для одной нелинейной задачи оптимального управления

В самом общем виде задача оптимизации может быть сформулирована следующим образом. Пусть имеется некоторое множество D c элементами

Y-4.0

z , которые будем называть допустимыми. На этом множестве задан функционал I (z). Требуется найти последовательность элементов z s из D , на которой функционал I(z) стремится к своей нижней грани на D , т.е. I(z s ) ^ inf I,z G D . Другими словами, речь идёт о поиске минимизирующей последовательности. Саму задачу для краткости будем обозначать (I, D ). При конкретизации каждой составляющей этой задачи будет получаться определенный класс задач оптимизации, такой как линейное или нелинейное программирование, оптимальное управление непрерывными или дискретными системами и т.д.

Существуют самые разнообразные подходы к решению конкретной задачи (I, D ). Одним из таких подходов является принцип расширения. Его суть состоит в переходе от исходной задачи к эквивалентной (L, E ), где функционал L есть модификация функционала I , определённая на более широком множестве E , включающем в себя D . Идея принципа расширения и первая его реализация принадлежит Лагранжу при решении задачи на условный экстремум. В роли функционала I фигурировала функция многих переменных, а в роли множества D — система равенств, состоящая из функций многих переменных. Минимизирующая последовательность должна была состоять из элементов, удовлетворяющих этой системе равенств. Лагранж предложил заменить исходную функцию некой конструкцией L , включающей в себя дополнительные слагаемые. Каждое из них представляло собой произведение одного из равенств на некоторый множитель. Тогда множество E совпадало с областью определения заданной функции, и на исходном множестве I и L совпадали. Конструкция L в дальнейшем получила название функции Лагранжа, а дополнительные множители стали множителями Лагранжа [1] .

Эта идея была реализована В. Ф. Кротовым для задач оптимального управления непрерывными и дискретными системами [2] . Как и у Лагранжа, производилось преобразование исходного функционала с помощью дополнительных конструкций, учитывающих ограничения на переменные состояния и управления. Вместо множителей Лагранжа фигурировала уже некая функция (функция Кротова). Позднее этот результат был распространен на дискретно-непрерывные системы и неоднородные дискретные системы [3 , 4] . Все указанные преобразования задачи (I, D ) к задаче (L, E ) производились по алгоритму предложенному В. Ф. Кротовым. Однако позднее В. И. Гурман высказал идею иного преобразования I в L по аналогии с методом штрафов и реализовал её на простом примере [5] .

В данной работе схема, предложенная в [5], использована для класса квазилинейных систем. Изложена методика преобразования, получаемый при этом алгоритм и иллюстративный пример. Для рассматриваемой в статье задачи далее используется эвристический прием аналогичный подходу SDRE [6].

Ниже рассматривается комбинация двух вариантов принципа расширения: сочетание расширения, предложенного Кротовым с расширением с использованием штрафных функций. Изложенный подход успешно реализуем для частных случаев управляемых систем: систем, близких к линейным, билинейных, линейно-квадратических с управляемыми коэффициентами и т.д., где возможны аналитические преобразования лагранжиана Кротова. Непосредственно в работе рассматриваются квазилинейные системы. В самом общем случае схема становится слишком громоздкой, трудно реализуемой и малоэффективной.

1.    Постановка задачи

Будем рассматривать следующую задачу оптимального управления:

dx

X = Ui = A(x, ^x + B(x, e)u, t e T = [ti, tF], где A, B — матрицы размеров n x n, n x r соответственно,

x(t) e R n ,    u(t) g R r ,

£ — параметр, e G (0,1]. Для модели (1) ставится задача о поиске минимума на D функционала

1                                                            1

(2) I =-   X T Q(x,e)x + u ^T S (x^u^dt + Nxf + xF^ Лx F

T при начальном состоянии x(ti) = x0. Здесь Q,S — заданные матрицы размера n x n, r x r соответственно, Q > 0, S > 0, Л — симметрическая, положительно определенная матрица размера n x n, N — вектор размера n.

2.    Преобразование задачи и поиск решения

Преобразуем задачу, используя вариант расширения класса допустимых, предложенный В. И. Гурманом в [5] , при этом будем предполагать, что все объекты обладают необходимыми для преобразований свойствами. Всё дальнейшее исследование проводится в предположении, что матрицы A , B , Q , S не зависят от x , что и определяет эвристический характер получаемого алгоритма.

Введём в рассмотрение ещё одно уравнение x = v, где v можно рассматривать как новое неограниченное управление. С учётом этого функционал представим в виде:

L _a = a J (v — A(x, e)x — B(x, e^uf (v — A(x, e)x — B(x, e)u)dt+ T

1                                                       1

.

+ (1 — a) I -   (x^TQ(x, e)x + u ^T S(x, e)u)dt + Nxf + -x T ^xf

T

Здесь a — весовой коэффициент, a G [0,1], а первое подынтегральное выражение — штраф за невыполнение уравнения связи. Следует заметить, что при α стремящемся к нулю все компоненты вектора v стремятся в бесконечность, т. е. по сути выполняют роль штрафных функций.

Воспользуемся далее конструкциями достаточных условий оптимальности Кротова [2] . Лагранжиан Кротова с использованием конструкций достаточных условий оптимальности этого же автора имеет вид:

L _a = G - У R _a dt,

T где

G = (1 — a)F (t _F ,x _F )+ ф(t _F ,x _F ) — ф(t _I ,x I ), x _F = x(t _F ), x I = x(t I ),

R _a = фТv — a(v — A(x, e)x — B(x, e)u)^T(v — A(x, e)x — B(x, e)u) —

• —    -(1 — a)(x ^T Q(x, e)x + u ^T S(x, e)u) + ф _t .

Здесь ф(t,x) — функция Кротова; F(t F ,xf ) = Nxf + 2 x T ^xf . Заметим, что максимум функции R _a равен либо нулю, либо const и она зависит от управления v квадратичным образом, найдём её максимум по этой переменной. Имеем:

R av   ^ф х

v =

— 2a(v — A(x, e)x — B(x, e)u) = 0.

Откуда

— ф_х + A(x, e)x + B (x, e)u.

Подставим найденное выражение для v в функцию R _α и выполним необходимые преобразования, обозначим результат как P _α .

P a = ф x (A(x,e)x + B(x,e)u) + ^^ (ф х ) ² —

• —    -(1 — a)(x ^T Q(x, e)x + u ^T S(x, e)u) + ф _t = const.

В свою очередь, полученная конструкция зависит от управления u также квадратичным образом. Из необходимых условий экстремума следует, что управление, доставляющее максимум функции Pα , имеет вид:

• (3)                       u1— S ^-1 B T ф х .

1 — a

Подставив это выражение в функцию P _α и выполнив необходимые преобразования, будем иметь:

M a = Pa( u ) = A T ф х Х + XT-¹ Tфх BS 1 B T ф х + ^{2(1 — a )}

+ 4a (ф х ) — ^(l — a)x T Qx + Фt ⁼ const.

Зададим функцию ф(t,x) в виде ф(t,x) = ф ^т (t)x + 2 x^Ta(t)x , где ф — вектор размера n, а a — симметрическая матрица размера n х n.

С учётом этого,

(ф ^т BS I B ф+

M _a = A T фх + |x^T aAx + Xta A ^t ax + Щф~ —у

+ф ^т BS ¹ B ^T ax + x^TaBS ¹ B ^T ф + x^TaBS ¹ B ^T ax') +

+ 7~ ^{ф Т ф} + ^{ф Т} 4 a

ax + x^T aф + x^T aEax

— -(1 — a)x ^T Qx + ф ^т x + x T ¹ ax = const .

Потребуем теперь, чтобы последнее выражение не зависело от состояния процесса. В итоге получим уравнения для нахождения вектора ψ и матрицы σ . Итак,

• (4)     ф = —A^T ф — -¹—Аф^т BS^-1B^T a + aBS^-B^T ф) —

2(1 — a )

^— 4a ^{( фТ a + aф ) ,}

a = —aA — A^T a —

2a(1 — a)

a(2aBS ^-1 B ^T +

+ (1 — a^E^a + (1 — a)Q.

Значения ф(tF) = —(1 — a)N, a(tF) = —(1 — a)Л. Следует заметить, что для матрицы σ получено дифференциальное уравнение типа Риккати. С учётом полученных для ψ и σ уравнений, выражение для Mα принимает вид:

M a = —--- т ф ^т (2aBS ^-1 B ^T + (1 — a)E )ф. 4 a (1 — a )

В последнем выражении от параметра ε зависят матрицы B и S ^{- 1} Максимум этого выражения даст новое значение параметра.

Для поиска параметра ε может быть использован градиентный метод и его разнообразные модификации. В частных случаях возможно аналитическое исследование выражения M _α и получение формулы для нового значения параметра.

3.    Алгоритм

• (1 )    Задаются начальное управление u I и значение параметра е ¹ .

• (2)    Решается исходная система уравнений (1) , в результате находится траектория x ^I .

• (3 )    Справа налево интегрируется система (4) для вектора * и система

• (5)    для матрицы σ.

• (4)    Находится новое управление и по формуле (3) и параметр е.

• (5)    Переход к пункту 2.

4.    Пример 1

Критерий окончания расчётов: разность между значениями функционала на соседних итерациях меньше заранее заданной точности вычислений.

Рассмотрим следующую задачу:

X = ( ех ) ² —

Здесь A = е ² х, B = формулы алгоритма

и, x(0) = 1, I = - У Е 2 (х ² + xu²)dt + x(1).

—Ел/x, Q = е ² , S = е ² х, N =1, Л = 0. Основные

имеют вид:

и = 7-----7-- 7= (а — 1)е/х

(* + ах),

* = —ЕХ* -

а = — 2е ² х^

1 + а 2а(1 — а) 1 + а

ψσ,

*(1) = а - 1,

2а(1 — а)

а² + (1 — а)Е 2 ,

^(1) = 0,

" а = 74+4 *2.

4а(1 — а)

На начальной итерации е ¹ = 1, u I = 2.

В таблице 1 представлено изменение функционала по итерациям при различных значениях параметра α.

На решение примера потребовалось 6 итераций. При этом значение функционала с 1 ⁰ = 1.1044 уменьшилось до 1 ⁶ = 0.8590; 0.5366; 0.5020 при

Таблица 1. Изменение значений функционала при различных значениях а по итерациям, R k = | I k — I k-1 |

α=0.3 α = 0.6 α=0.9 k εk Ik Rk εk Ik Rk εk Ik Rk 0 1 1.1044 1 1.1044 1 1.1044 1 0.7588 0.9422 0.1622 0.2669 0.6944 0.4100 0.0528 0.8925 0.2119 2 0.7695 0.8637 0.0785 0.2738 0.5626 0.1318 0.0529 0.5392 0.3533 3 0.7644 0.8626 0.0011 0.2675 0.5429 0.0197 0.0528 0.5107 0.0285 4 0.7628 0.8599 0.0027 0.2668 0.5386 0.0043 0.0528 0.5046 0.0061 5 0.7624 0.8592 0.0007 0.2667 0.5372 0.0014 0.0528 0.5027 0.0019 6 0.7622 0.8590 0.0002 0.2666 0.5366 0.0006 0.0528 0.5020 0.0007 a = 0.3;0.6;0.9 соответственно. Графики управляющего воздействия и состояния процесса на первой и последней итерациях при a = 0.6 даны на рисунке 1.

1,2

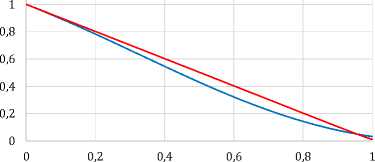
— Начальное состояние x(t)

---Состояние x(t) последней итерации

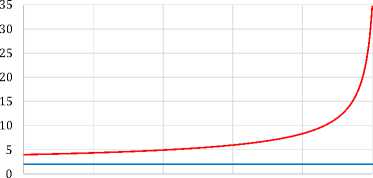
0           0,2          0,4          0,6          0,8           1

---Начальное управление u(t)

---Управление u(t) последней итерации

Рисунок 1. Графики состояния x(t) и управляющего воздей ствия u(t) по итерациям при а = 0.6

5.    Пример 2

Рассмотрим следующую задачу:

x = (ex)² — e sin(x)u, x(0) = 0.5,

I = - У e ² (x ² ^x + (xu) ² )dt — x(1).

Здесь A = e²x , B = —e sinx, Q = e²^x , S = (ex) ² , N = —1, Л = 0.

Основные формулы алгоритма имеют вид:

u =

sin x

(a — 1)ex ²

(ф + ax),

;            .2 / ф = —exф —

sin ² x       1

I. (T—^? ⁺ 2a) ^фа

a = —2e ² xa —

sin ² x

(1 — a)x ²

+

л

2a

a ² + (1 — a)e²^x,

ф (1) = 1 — a,

a (1) = 0 ,

1           sin ² x

^M a = 40(1—0) ²'    ⁺¹ — “И

На начальной итерации e I = 0.7, u I = —0.5. В таблице 2 обозначим

R k = | i k — i k^-1 |. в этой таблице представлено изменение функционала

Таблица 2. Изменение значений функционала по итерациям при различных значениях α

α=0.4 α=0.6 k εk Ik Rk εk Ik Rk 0 0.7 -0.8328 0.7 -0.8328 1 0.5888 -0.9632 0.1304 0.2583 -0.8668 0.0340 2 0.6022 -1.0268 0.0636 0.2621 -0.8973 0.0305 3 0.5998 -1.0272 0.0004 0.2624 -0.9018 0.0045 4 0.6004 -1.0273 0.0001 0.2620 -0.9007 0.0011 5 0.2619 -0.9006 0.0001 по итерациям с 10 = —0.8328 до 14 = —1.0273 и 15 = —0.9006 при значениях параметра a = 0.4 и 0.6 соответственно. Графики управляющего воздействия и состояния процесса на первой и последней итерациях при a = 0.4 даны на рисунке 2.

Заметим, что минимум функционала в обоих примерах существенно зависит от выбора весового коэффициента α .

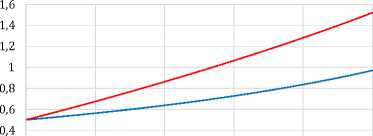
0,2

0           0,2          0,4          0,6          0,8           1

---Начальное состояние x(t)

---Состояние x(t) последней итерации

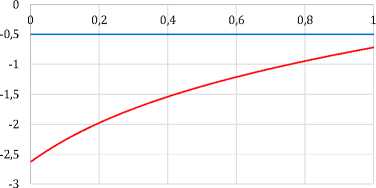
---Начальное управление u(t)

---Управление u(t) последней итерации

Рисунок 2. Графики состояния x(t) и управляющего воздействия u(t) по итерациям при а = 0.4

Заключение

На классе квазилинейных систем рассмотрен еще один вариант реализации принципа расширения, предложенный В. И. Гурманом в [5] , сочетающий традиционный подход Кротова [2] и идею использования штрафных функций [1] . Полученный алгоритм апробирован на двух иллюстративных примерах. В результате расчетов построены минимизирующие последовательности. Его трудоемкость по количеству итераций практически не отличается от алгоритма, основанного на традиционном варианте принципа расширения [7] , что подтверждает его работоспособность. Область его применения отмечена во введении.