Эвристический подход к классификации послеродового эндометрита и его форм

Повышение доли современного оборудования, позволяющего выполнить анализ состояния большого количества параметров организма, лавинообразно увеличило количество поступающей к врачу информации, но не облегчило процесс постановки диагноза.

Внедрение информационных технологий обработки результатов анализов в практику работы врача привело к появлению автоматизированных методов диагностики. Адаптация методов диагностики [2], созданных для технических

объектов сталкивается с неприятием в медицине, в силуразличия подходов к описанию состояния объекта у медиков и математиков, и большимраз-нообразием значений медицинских параметров, в отличие от технических объектов.

Проблема разработки методов автоматизированной медицинской диагностики понятных врачу, а потому принимаемым им в практику работы, весьма актуальна. Системы поддержки принятия решений, созданные на базе таких методов, относят состояние пациента к одному из заранее определенных классов состояний, окончательный диагноз по-прежнему устанавливается врачом.

Целью данной работы является выработка информационного подхода к медицинской диагностике, основанного на выделении наиболее значимых симптомов (эвристических признаков) заболевания и методах их обработки, а также создание системы автоматизированной медицинской диагностики вырабатывающую рекомендации для врача, обладающего меньшей квалификацией.

Материал и методы

Для описания состояния объекта исполь- зуются как детерминированные, так и вероятностные модели. Детерминированная модель требует информации об элементах системы и связях между ними и применима только в случае систем, состоящих из ограниченного числа элементов. В медицине это, как правило, модели достаточно простых процессов, например, оценки функционального состояния сердечно-сосудистой системы [1], функционирования фолликула щитовидной железы [4], злокачественной опухоли [6]. Детерминированные модели при описании даже простых процессов используют сложный математический аппарат. Адекватные действительности решения существуют для ограниченного диапазона начальных условий. Увеличе-ниечисла элементов системы, приводит к росту числа уравнений, описывающих связи между ними, и потере устойчивости решений. В этой связив задачах медицинской диагностики, где состояние объектаопределяется совокупностью множества факторов, детерминированные модели неприемлемы, а используются вероятностные модели, характеризующиесостояние объекта усредненными параметрами.

Любую биомедицинскую систему можно охарактеризовать двумя параметрами: энергией, как мерой движения и взаимодействия ее элементов, и энтропией, как мерой упорядоченности этой энергии, заключенной в организации системы. Функционирование биомедицинской системы основано на циклических процессах, связанных с транспортом внешней энергии и диссипацией этой энергии. Поэтому обобщенную модель открытой биомедицинской си- стемы можно представить в виде замкнутого энерго-энтропийного цикла, изображенного на рисунке 1.

Без транспорта высокоорганизованной энергии Е 1 энтропия системы увеличивается по пути 1–2. Если нет поступления высокоорганизованной энергии, то число возбужденных элементов стремится к нулю, система приходит в равновесное состояние с окружающей средой (погибает).

В точке 2 системе сообщается энергия Е 1 , часть которой идет на увеличение числа возбужденных элементов системы, чтобы компенсировать их уменьшение в процессе увеличения энтропии. В результате увеличивается температура системы (участок 2–3) и происходит уменьшение энтропии до исходного состояния (участок 3–4). При этом наступает уменьшение температуры до первоначального уровня, и система возвращается в исходное состояние, т. е. цикл замыкается. Каждому такому циклу отдельной системы организма соответствует свой биологический ритм.

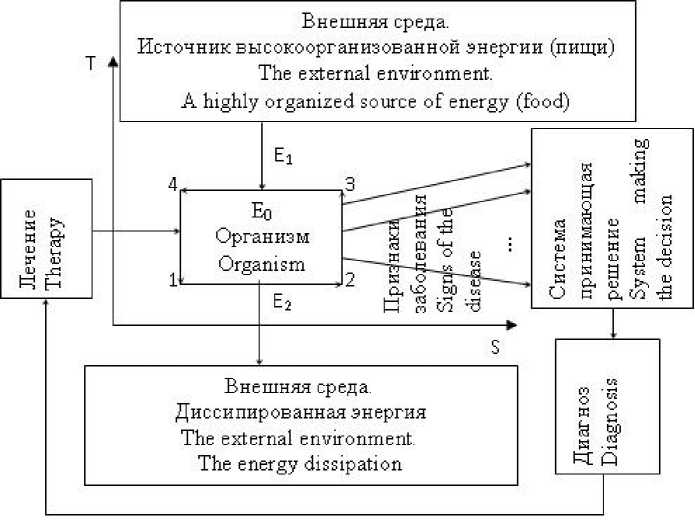
Рисунок 1. Модель открытой биомедицинской системы

Figure 1. Model of open biomedical systems

Нарушение энерго-энтропийного цикла свидетельствует о патологии той или иной системы организма, что выражается в N симптомах заболевания. Эти признаки определяются отклонением от нормы числа возбужденных и невозбужденных элементов системы, реализуемых в биологическом цикле. Так как связь между признаками состояния систем организма и характером возбуждения их элементов статистическая, то развитая модель является вероятностной. Признаки заболевания анализируются решающей системой (врачом или компьютером). Результатом анализа признаков является диагноз, и назначается лечение, которое реализуется по цепи обратной связи (рисунок 1) .

Наибольшее применение в практике нашли параметрические и эвристические методы классификации заболеваний [7, 8]. Параметрические методы позволяют сделать оценку вероятностей правильной классификации заболевания, его пропуска и гипердиагностики, что позволяет сравнивать точность классификации на основе различных симпотмокомплексов. Эвристические методы естественным образом сочетаются с практикой работы врача, следуют из его знаний и опыта, позволяют быстро модифицировать и совершенствовать выбранные системы признаков.

В этой связи наибольшую эффективность для целей автоматизированной медицинской диагностики может дать синтез параметрического и эвристического подхода [9].

Симптомы заболевания могут быть как количественными (измеряются с помощью аппаратуры и выражаются в числовом значении), так и качественными (характеризуют некоторое состояние и не могут быть измерены) [11]. Математический анализ их совокупности возможен лишь в случае, когда они имеют одинаковую размерность, либо все симптомы безразмерны. Переход к безразмерным значениям осуществляется в соответствии со следующими соображениями.

Для диагностики заболевания каждый симптом должен принадлежать конкретному диапазону значений, например, при воспалительных заболеваниях температура тела изменяется от 37,5 до 39 °С. Поэтому не столько важно конкретное значение симптома, сколько его попадание в указанный диапазон. Разбив все признаки заболевания на диапазоны значений, соответствующих различным нозологиям, получим для всех симптомов одинаковую характеристику – число диапазонов (число градаций симптома), на основании которой можно вести математический анализ клинической картины.

Организация системы признаков заболеваний (симптомокомплекса) представлена на рисунке 2, где по оси абсцисс расположены N признаков заболевания, а по оси ординат – количество двоичных единиц log 2 n , соответствующих измеряемому числу градаций n каждого признака.

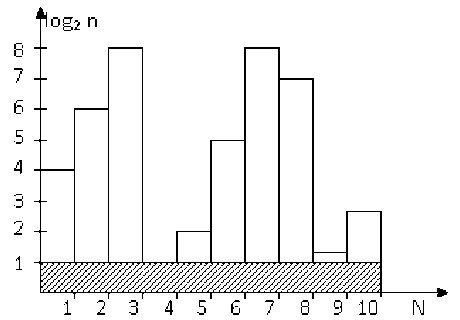
Рисунок   2.   Информационная организация симптомокомплекса

Figure 2. Information organization of symptom

Качественные признаки имеют две возможные градации: отсутствие признака – норма, и наличие признака – болезнь, а также граница норма – болезнь. В случаенормы n = 2 и признак дает 1 бит информации. Начальным уровнем отсчета количественных признаков является его среднее нормальное значение. На рис. 2 заштрихованные участки признаков соответствуют градациям нормы, а незаштри-хованные – болезни.

Поскольку заболевание сопровождается появлением как общих, так и специфических симптомов, то каждый из них несет разное количество информации. Совокупные данные, получаемые при анализе всех симптомов, для того или иного заболевания будут различны. Следовательно, можно выбрать граничные значения информации о каждой нозологической форме и ставить диагноз на основании сравнения полученного количества информации о состоянии больного с граничным значением информации о заболевании.

Оценить необходимость включения в рассмотрение нового симптома можно, рассчитав общее количество информации для нового симп-томокомплекса. Если оно увеличилось по сравнению с предыдущим, то симптом включается, если уменьшилось – исключается из рассмотрения.

Оценку информационной емкости симп-томокомплекса выполним по Хартли, тогда сообщение нормальному состоянию организма N соответствует Сн = ^log2 nHi = N, а патологи-i=1

N ческому Сб = ^ log2 n6i .

i = 1

С учетом вероятности обнаружения P каждого признака информационную емкость системы N независимых признаков можно записать следующим образом

N

Сб = ЕРоб, log2 ni i=1

или

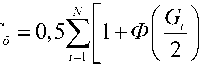
log₂ n_i ,

где Ф – интеграл вероятности, G – аппаратурное отношение сигнал/шум,

Отношение площадей незаштрихованных и заштрихованных участков на рис. 2 назовем отношением болезнь / норма

G о = 77" .                 (2)

Cн

Решение о наличии болезни будет приниматься при превышении сигнала болезни порогового уровня нормы. В этом случае вероятность распознавания болезни можно записать следующим образом:

P * = Ф ^f G )

I 2 )

В простейшем случае вероятность распознавания болезни не зависит от числа признаков, если их число не менее 2.Это вызвано тем, что с повышением информационной емкости системы признаков пропорционально увеличи-ваетсяэнтропия решающей системы, вследствие обучения и распознавания по одной и той же обучающей выборке. Использование только качественных признаков (n =2) неэффективно, так как вероятность распознавания болез-нине превышает0,5.

Возможность оценки вероятности заболева *

ния P повышает достоверность метода, однако для близких форм заболевания сложно найти пороги, разделяющие объекты с высокой точностью.

Для разделенияблизких форм выявленного с вероятностью P ^* заболевания следует использовать подход, основанный на оценке степени

«похожести» диагностируемого случая с рядом уже имеющихся, образующих кластер.

На первом этапе (обучения системы поддержки принятия решений) формируются кластеры для диагностируемых заболеваний по обучающей выборке, на втором (рабочий режим системы) проводится анализ состояния конкретного больного. Диагноз выбирается из того кластера, к которому ближе всего оказался рассматриваемый случай. Кластерный анализ позволяет установить степень тяжести заболевания.

Диагностика степени тяжести заболевания осуществляется с использованием кластерного анализа в выбранном пространстве медицинских признаков в соответствии со следующим алгоритмом. Дисперсия каждой формы заболевания D^ф (легкой, средней и тяжелой) вычисляется по формуле:

M

D = —У( х ф - x ф)        (4)

M     i где ф – наименование формы заболевания – легкая, средняя или тяжелая; М – число пациентов в выборке с заболеванием со степенью тяжести ф; xiф, xф –значение признака заболевания для рассматриваемого i-того пациента и среднее значение этого признака по всей имеющейся обучающей базе данных для отдельной формы заболевания.

Центром кластеров, соответствующих формам заболевания, являются средние значения признаков по каждой форме. Форма кластеров в простейшем случае может быть окружность в двумерном признаковом пространстве, сфера –в трехмерном и гиперсфера – в N – мерном пространстве признаков. Радиус гиперсферы есть среднее геометрическое значение дисперсий каждого признака, образующих признаковое пространство.

N

^{R #} =.Е ( D ! )             (5)

v j = 1

где N – число информативных признаков, характеризующих заболевание; j – текущий номер признака.

Для дифференциальной диагностики заболеваний решающее правило имеет следующий вид: рассматриваемая точка принадлежит кластеру той формы заболевания, для которой проекция расстояния от центра кластера до точки на прямую, соединяющую центры двух соседних кластеров, не превышает половины межцентрового расстояния соседних кластеров:

П > — гс ф ф ² ^ т е ф

П < — гсф ф2 ^ т е ф где гсф ф2 -межцентровое расстояние кластеров форм заболевания ф1 и ф2; m – рассматриваемая точка.

В соответствии с изложенной методикой синтез системы поддержки принятия решений осуществляется в следующей последовательности.

• 1.    С помощью врача-эксперта выделяются заболевания и его формы и собирается статистика, содержащая не только симптомы патологии, но и заранее определенные диагнозы;

• 2.    Производится усреднение значений симптомов в рамках выделенных экспертом диапазонов, важных для определения нозологии.

• 3.    Итерационным путем отбираются наиболее информативные симптомы заболевания, закладываемые в обучающую выборку, обеспечивающие максимальные значения вероятности классификации заболевания;

• 4.    Производится расчет вероятности классификации (3) для всей обучающей выборки и определяются пороги классификации, позволяющие разделить объекты на находящиеся в пределах нормы и имеющие патологическое состояние. Выполняется оценка возможности выбора порогов для классификации отдельных форм заболевания.

• 5.    Производится классификация состояния пациента на основании сравнения расчетного значения вероятности классификации (3) с пороговым значением.

• 6.    Выявленные на предыдущем этапе случаи патологии подвергаются дифференциальной диагностике на основании кластерного анализа (4–6) для установления формы заболевания.

После этого система поддержки принятия решения готова к функционированию в консультационном режиме, позволяя в процессе эксплуатации системы врачом получить альтернативы диагноза. Консультационный режим состоит из:

• 1.    сбора и ввода в систему данных о новых пациентах, составляющих максимально информативный симптомокомплекс;

• 2.    автоматический расчет в соответствии с предложенной методикой и выдачу предполагаемого диагноза.

Врач ставит диагноз на основании полученных рекомендаций.

Принципиальной трудностью, возникающей при распознавании состояния пациента, является оценка минимально возможной мощности обучающей выборки и числа градаций признаков, обеспечивающих заданную вероятность классификации.

Существующая аппаратура может обеспечить чрезвычайно высокую точность измерений. При этом информационная емкость сигнала, поступающего в систему управления, может быть значительно большей, чем емкость обучающей выборки, что снижает вероятность правильного предсказания состояния системы [3]. Следовательно, возникает проблема согласования относительно невысокой информационной мощности обучаю- щей выборки и информационной емкости сигнала, обеспечиваемого современными средствами контроля, при сохранении заданной вероятности правильного предсказания состояния управляемой системы.

Для надежной диагностики состояния пациента достаточно весь динамический диапазон изменения признаков разбить не более чем на 16 градаций, а в пределах каждой градации производить усреднение значений. Наличие статистики заболеваний позволяет уменьшить необходимое число градаций. Однако эвристический подход к установлению порога требует определенного запаса по числу градаций сигнала, область изменения которых в зависимости от мощности обучающей выборки можно задать следующим образом 8 ≤n≤ 20 .

Очевидно, что число градаций статистического ряда обучающей выборки, также как и число градаций сигнала, должно быть связано с мощностью обучающей выборки. При слишком большом числе градаций частоты статистического ряда имеют незакономерные колебания. При слишком малом числе градаций описание очень грубое. Поэтому даже если информационная емкость обучающей выборки близка к информационной емкости сигнала, число градаций в пределах заданного выше диапазона должно сочетаться с объемом выборки. В [3] установлен минимально возможный объем статистического ряда

n

L ≥ 10 ⁵ , (6)

откуда следует, что 40 ≤L≤ 10 ⁴.

При проверке корреляционной связи между признаками и отборе статистически независимых, их число может быть существенно уменьшено.

Предложенный подход был апробирован для диагностики послеродового эндометрита, часто протекающего атипично и являющегося одним из самых трудно диагностируемых заболеваний, особенно в его легкой и средней формах [5, 12, 13]. Диагностировался послеродовой эндометрит и его формы, отражающие степень тяжести заболевания: легкую среднюю и тяжелую. Собранная база данных включала 70 историй болезней.

Результаты и обсуждение

Интервал дискретизации каждого признака системы и число их градаций определялись путем усреднения по различным интервалам статистического распределения признака с выделением трех экстремумов, соответствующих легкой, средней и тяжелой формам заболевания. Увеличение интервала усреднения приводит к объединению соседних форм заболевания, уменьшение – к росту числа случайных экстремумов.

Были определены границы диагностики трех форм заболевания (легкой, средней и тяжелой) и сформированна и более информативный симп-томокомплекс, включающий количественные признаки: температуру тела, число лейкоцитов при бактериоскопии мазка, данные эхографии (длину, толщину и передне-задний размер матки), кровопотерю, бактериологическое исследование содержимого матки,толщину послеоперационного шва на матке, изменение длины полости матки при зондировании; и качественные: характеристику лохий, особенности кесарева сечения (плановое или экстренное), состояние полости матки (при гистероскопии), наличие патологических включений в полости матки, форма полости матки, состояние послеоперационного шва на матке (налет фибрина, провисание лигатур), гиперемию.

Оценка вероятности распознавания заболевания произведена с использованием соотношения (3) и определен порог нормы 0,848 . Удалось абсолютно достоверно диагностировать эндометрит и отделитьвсе его тяжелые случаи. Пороговое значение вероятности классификации для отделения тяжелой формы составил 0,965 .

Дифференциальная диагностика форм легкой и средней форм эндометрита осуществлялась с использованием кластерного анализа в выбранном пространстве признаков.Обучаю-щая выборка по формам заболевания была неоднородной с перекосом в пользутяжелой формы ( 81,4 %,). Объем выборки по средней форме составил 8,6% , а по легкой – 10% . Большая разница в объемах обучающих выборок по каждой форме привела к тому, что дисперсии кластеров легкой и средней форм оказались существенно большими, чем для тяжелой. Однако размеры кластеров легкой и средней формы эндометрита примерно одинаковы, поэтому удалось получить достаточно высокие результаты. Верно диагностированы 85,7% случаев легкой (6 из 7 имеющихся в обучающей выборке), 83,3% – средней (5 из 6).

С помощью двухступенчатой автоматизированной диагностики заболевания были форм послеродового эндометрита. Результаты автоматизированной диагностики эндометрита и его форм приведены в таблице 1.

Таблица 1.

Результаты диагностики

Table 1.

The results of the diagnostics

№	Показатели | Index	Формы эндометрита | Forms of endometritis
		Легкая | Light	Средняя | Middle	Тяжелая | Heavy
1	Размер выборки | The sample size	7(10%)	6(8,6%)	57(81,4%)
2	Пороги P * | Limit	0,848	0,858	0,965
3	Верные диагнозы | The correct diagnosis	6(85,7%)	5(83,3%)	57(100%)

В результате из 70 случаев эндометрита в легкой, средней и тяжелой форме системой поддержки принятия решений была верно определена степень тяжести заболевания у 68 родильниц, что составляет 97,1%.

Заключение

• 1.    Предлагаемый эвристический подход позволяет надежно распознавать заболевание и диагностировать достаточно близкие его формы в условиях статистической недостаточности обучающей выборки, которую во многих случаях невозможно улучшить вследствие особенностей протекания заболевания.

• 2.    Изложенная методика классификации может быть реализована в реальном масштабе времени, когда диагностируемые сигналы