Joint Decoding Technique for Collision Resolution in Non-orthogonal Multiple Access Environment

A heterogeneous data transfer environment is the new normal for wireless communication technologies considering the heavy data usage by consumers nowadays [1]. Due to this, the recent wireless communication technologies have adopted sophisticated multiple access that helps in improving the heterogeneous data transfer paradigm [2]. The multiple access technologies are categorized as Orthogonal Multiple Access (OMA) and NOMA techniques. With 5G technologies emerging the NOMA techniques are abundantly used [3] considering their multiple access capabilities. In particular, NOMA techniques can be divided into two groups: code-domain NOMA and power-domain NOMA [4]. Superposition coding is applied at the base station for combining signals from different users during the transmission stage and Successive Interference Cancellation (SIC) is implemented to reduce interference in the received signal [5]. A time/frequency Resource Block (RB) is efficiently used by the power-domain

NOMA for multiple users with SC techniques at the transmission side and SIC at the receiver side [6]. A two-user game is analyzed on the NOMA random access platform to check the performance of transmission probability and pay off region [7]. The throughput and the access fairness of the NOMA random access system is controlled by optimally choosing the transmission probability and target receive power [8, 9]. NOMA being advantageous than the previous multiple access systems from the first generation to the fourth generation is the choice for the 5th generation wireless communication system. A major drawback of the NOMA system is the collision occurring while multiple users communicate with the single base station. Thus, collision resolution or collision reduction algorithms take the center stage while NOMA implementation is developed. A collision resolution period (CRP) is introduced in the NOMA implementation where the collided packets are transmitted to improve the throughput and transmission probability [10]. Multiple signals when approaching the base station uses the RB which has stipulations. Thus, round trip delay (RTD) of the signals is estimated which helps to improve the throughput by implementing SIC in the time domain [11]. Even numbers of signals are estimated using RTD. SIC based NOMA and proportional fair scheduling based multiuser diversity (MUD) is combined by switching between these two algorithms to obtain a high sum-rate gain in a multi-access environment [12]. Estimation of number of users and simultaneously controlling the transmission capability of the user is possible using the online method applying Bayesian approach [13].

The literature review is presented in Section 2 on scrambling, coding, interleaving, and spreading-based NOMA schemes. Section 3 explains the paper's contribution. Section 4 presents Joint Decoding on NOMA Strategy. Section 5 explains the experimental results and discussion for forward error correction codes Viterbi, LDPC and Turbo for both far and near users. The conclusion of the proposed research work is contained in Section 6.

2.    Related Works

NOMA based techniques have outperformed traditional techniques both in improving the throughput and collision probability [14]. A vehicle-to-anything application uses time frequency resource to avoid collision in the NOMA environment. It uses the uncoordinated transmission of data by means of specially designed transmit signatures and the receiver that utilizes this signature structure [15]. Different NOMA schemes including the scrambling-based NOMA, coding-based NOMA, interleaving NOMA, spreading based NOMA and coding based NOMA are discussed in the literature [16, 17]. Physical layer NOMA uses LDPC algorithm for on the bit interleaved coded multiple access implementation. Multiuser interference is largely reduced since LDPC encoder is adopted in the implementation [18]. Performance of the NOMA implementation improved while LDPC encoder and decoder are used for transmission and receiver side respectively [19]. The computational complexity of the NOMA implementation is kept in an acceptable level while both conventional and cooperative LDPC is implemented in the NOMA paradigm [20]. Higher throughput is achieved in the multiple-access wireless communication paradigm enabling both the collision resolution and decoding [21]. Random Access LDPC (RA LDPC) is introduced in the multiple access paradigms. Nested LDPC is added in the random-access coding strategy in the implementation and error exponent analysis is found to be satisfactory [22]. The throughput of the NOMA network can be concluded when taking the comparative analysis between Viterbi, LDPC, and Turbo codes. There is a percentage improvement in BER from SIC to SIC-Viterbi, SIC-LDPC, and SIC-Turbo codes. The obtained experimental results provide using SIC-Turbo codes an increase in BER values when compared to other codes.

3.    Paper Contribution

Various block coding algorithms are used in random access paradigm [23, 24] to improve the performance of data delivery in wireless communication systems by improving the throughput and reducing the interference in the data. NOMA implementation in 5G environment are applied for better performance by optimizing the power allocation using meta-heuristic method [25, 26] and automated user installation [27]. This paper exploits the capability of NOMA paradigm in utilizing the available resource efficiently with higher quality of service maintained in the wireless communication paradigm. This paper applies the joint decoding along with the SIC algorithm in the NOMA environment. A performance comparison of Viterbi, LDPC and Turbo code on the NOMA implementation is developed and the Bit Error Rate and throughput for each algorithm on NOMA environment is developed.

4.    Joint Decoding on NOMA Strategy

NOMA implementation with collision resolution using SIC is extended in this implementation combining the forward error correction codes with the SIC implementation in the receiver end. NOMA is implemented in power domain-based implementation where the users using the same time and frequency resources are multiplexed. The type 2 collision resolutions are considered in this implementation with SIC as the first level and decoding using forward error corrections codes for collision reduction. In data transmission systems, forward error correction (FEC) continues to play an extremely important role. A limited number of errors in transmitted data can be found and fixed using the forward error correction (FEC) technique without the need for retransmission. In this approach, the sender additionally includes an error-correcting code in the data frame. The additional redundant bits are used by the receiver to perform the necessary checks. If it determines that the data is error-free, it runs the code that creates the actual frame to correct any errors. Before sending the message to the upper layers, it then eliminates the unnecessary bits. FEC allows for the simultaneous broadcasting of data to numerous destinations from a single source without the need for handshaking between the source and the destination. FEC also reduces the amount of bandwidth needed for retransmission. As a result, real-time systems use it. When two users use the same frequency simultaneously in the multiple access networks the SC is used to multiplex the data (x1 and x2 for each user) from these two users. Different power levels of the users are defined and assigned to the user data and then these two data are added which is defined as SC. Power level (a1 (far user) and a2 (near user) for each user) defines the priority given to each of the user data. The resultant signal (x) from the SC is the generated using equation (1).

x = 40 1 x 1 + 40 2 x 2 (1)

Thus, higher spectral efficiency is achieved by using the SC in the NOMA signal thus generated as given in equation (1). With the transmit power applied on the superimposed signal the equation (1) is derived as equation (2).

x = 4P(40 1 x 1 + 40 2 x 2 )

Where P is the transmit power for the NOMA signal thus superimposed. The SC signal is the linear combination of both the user data. To the SC response from the equation (1) BPSK modulation is applied on the signal which is superimposed combination of both the user data. The modulated signal is considered to be passing through the Rayleigh fading channel. The Rayleigh fading is modeled as given in the equation (2). The Rayleigh channels for two user data are defined as the term h1 and h2. Although the SC signal passes through both the channels as given in equations (3) and (4). After propagating through the Rayleigh channel, the received signal for near user is,

У 1 = h 1 x + w 1

And for far user is,

У 2 = h 2 x + W 2                                            (4)

Expanded the equation (3) meant for the near user by substituting (2) in (3) equation (5) is obtained.

У 1 = h 1 4P(40 1 x 1 + 40 2 x 2 ) + w 1

Further expanding the equation (5) equation (6) is obtained with three separate terms: dominating signal, low power signal and the noise. The first term is the dominating term followed by low power and noise terms in equation (6).

У 1 = h₁4P40 1 x₁ + h 1 4P40 2 x₂ + w 1

Since the power allocation for the far signal is higher than the near signal the equation (6) directly decoding the equation (6) gives the far signal values. While for the near signal SIC is applied using the equation (7).

У ‘ =У 2 - 40 1 x 1

Where x 1 which is estimate of signal x 1 is found from the equation given in equation (8).

У 2 = h 2 4P40 1 x 1 + h ^ ^PjCx + W 2

The estimate of the signal x2 is found by decoding the equation (7). SIC implementation is accompanied with the forward error correction codes Viterbi, LDPC and Turbo. Both near and far signals is encoded using these codes before SC is applied on the signals to evaluate the collision resolution in the NOMA paradigm using these encode decoder pairs. The block diagram of the proposed implementation is shown in fig. 1.

Joint decoding implementation uses both the SIC and forward error correction (FEC) algorithms for collision resolution in the NOMA environment with Rayleigh fading channel. The FECs encode the user data individually before the SC is applied to the data and, decades after the estimation from the SIC. Thus, this sequential encoding is defined as joint encoding. MATLAB-based implementation is developed in the NOMA environment for the proposed method and results are discussed in the following section. Viterbi encoding is the convolution-encoded method while LDPC and Turbo methods are blocked encoding methods.

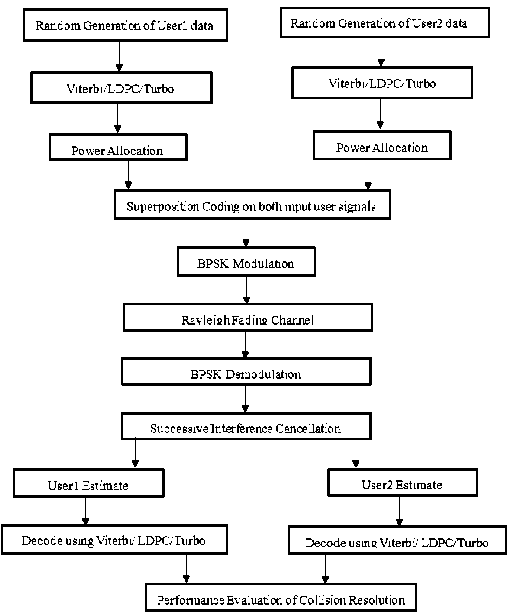
Fig.1. Joint decoding based collision resolution

Viterbi generates the convolution codes using the generator polynomials. The Viterbi algorithm generates the trellis diagram for the input data with the defined code rate in table 2 with the polynomial form as given. Encoded data after the decoding from the SIC algorithm is decoded using the Viterbi algorithm back tracing the Trellis structure. Similarly; LDPC encoding is developed by a generator matrix that is the combination of both the parity matrix and the data to be encoded. Parity matrix H is developed by permutation combination knowing the code rate. Tanner graph that maps the input data on the output data allocates the mapping code for the data transition. After the SIC decoding the iterative LDPC decoder is used that uses Log Likelihood ratio to get the decoded data. Turbo decoder is developed using the unique trellis structure. Two or more components’ encoders concatenated in parallel and then separated by interleaver. Soft decision algorithm is used to decode the data from the SIC output in the Turbo Decoder paradigm.

5.    Results and Discussion

The simulation specification of the MATLAB implementation of the method is given in the table 1. NOMA for two users and type 2 collisions is developed and results are observed for all the three different joint decoding implementations.

Table 1. NOMA implementation specifications

Parameter	Units	User1	User2
Distance from base station	meters	1000	500
Range of Transmit Power	bBm	0 to 40	0 to 40
System Bandwidth	MHz	1	1

Collision resolution implemented on the NOMA implementation with two users gives the BER graph as given in fig. 2. The obtained simulation results give the BER for all the decoding techniques. To achieve Quality of Service (QoS) the BER value should decrease. From fig. 2 the dark line represents the SIC values and dotted points indicate the theoretical values. The BER values and theoretical values are at the same track line. Hence the BER is found to be tracing the theoretical values. The parameters are fixed for all four algorithms' decoding techniques and a comparative analysis is given in table 2.

Table 2. Joint decoding specifications

SIC Parameters	SIC-Viterbi Parameters	SIC-LDPC Parameters	SIC – Turbo Parameters
Number of Data bits 64800	Number of Data bits 64800	Number of Data bits 64800	Number of Data bits 64800
Distances of users from base station (BS) d1=1000, d2=500	Distances of users from base station (BS) d1=1000, d2=500	Distances of users from base station (BS) d1=1000, d2=500	Distances of users from base station (BS) d1=1000, d2=500
Power allocation factors a1 = 0.75; a2 = 0.25	Power allocation factors a1 = 0.75; a2 = 0.25	Power allocation factors a1 = 0.75; a2 = 0.25	Power allocation factors a1 = 0.75; a2 = 0.25
Path loss exponent= 4	Path loss exponent= 4	Path loss exponent= 4	Path loss exponent= 4
	Constraint Length=3, Code Generator Polynomial [2 3 5] Hard decoding	Code Rate =1/3; Decision Method: 'Soft decision' Maximum Iteration Count: 50	Trellis Structure (4, [13 15 17], 13)

With the above parameters all four implementations compare with the theoretical values.

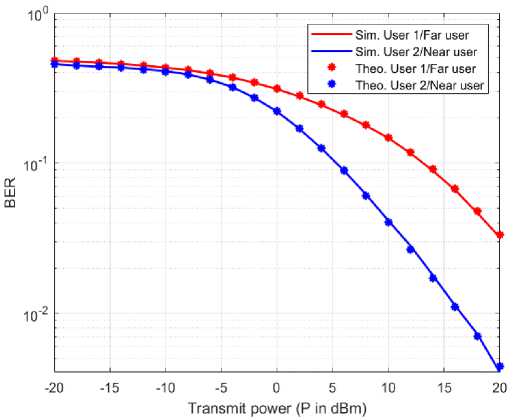
• Fig.2.    BER graph for NOMA with SIC

NOMA collision resolution using the Viterbi algorithm is applied with the 1/3 code rate. The output from the SIC is given as the input to the Viterbi decoder to obtain the BER graph as given in the fig. 3. The obtained simulation result is less than the theoretical values. Thus, the BER obtained is less when compare to NOMA with SIC.

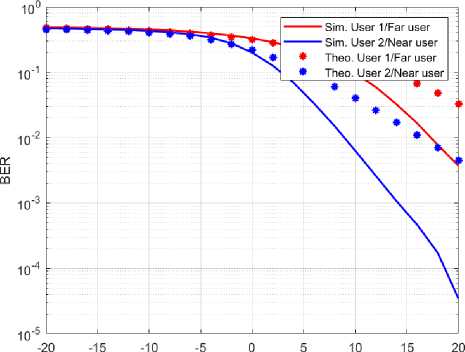
Transmit power (P in dBm)

• Fig.3.    BER graph for NOMA with SIC-Viterbi

It can be observed that the BER from the collision resolution implemented using the SIC-Viterbi algorithm provides the BER competitive than the SIC implementation.

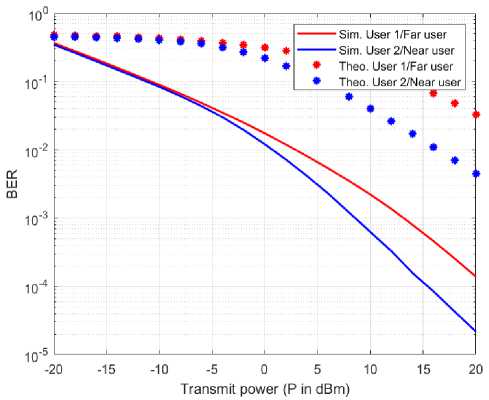
• Fig.4.    BER graph for NOMA with SIC-LDPC

  

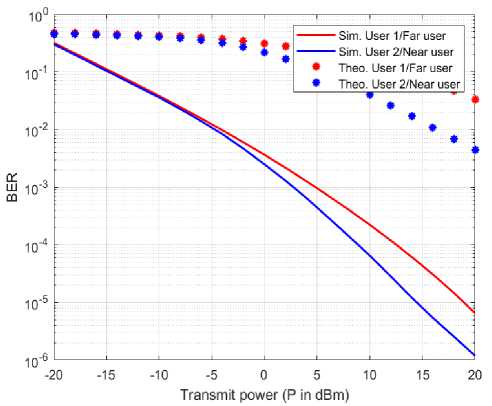
• Fig.5.    BER graph for NOMA with SIC-Turbo

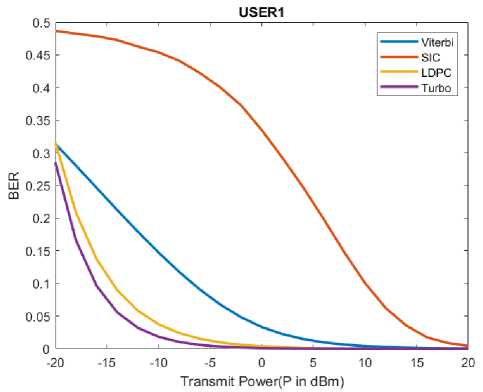
It can be observed from the fig. 4 and fig. 5 implementation that the Turbo and LDPC based implementation has obtained the better than the SIC and SIC-Viterbi implementation. The BER comparison for both the user1 and 2 are for all the considered method is as given in the following graphs as shown in fig. 6 and fig. 7.

• Fig.6.    User1 BER comparison

  

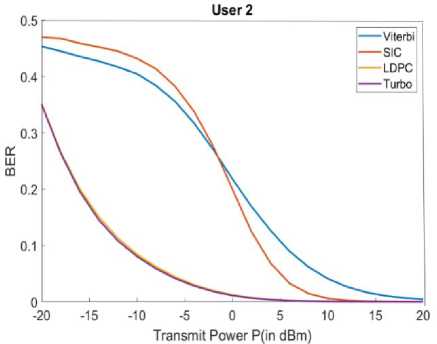
Fig.7. User2 BER comparison

The table of the BER from all the methods discussed is given in table 3 and table 4.

Table 3. SIC and SIC-Viterbi BER

Transmit Power (in dBm)	SIC		SIC-Viterbi
	User1	User2	User1	User2
-20	0.475586419753086	0.453395061728395	0.486265432098765	0.469598765432099
-10	0.430864197530864	0.404614197530864	0.451728395061728	0.431990740740741
0	0.309043209876543	0.218240740740741	0.330277777777778	0.199891975308642
10	0.146790123456790	0.0410648148148148	0.0936574074074074	0.00606481481481481
20	0.0329938271604938	0.00450617283950617	0.00402777777777778	3.08641975308642e-05

Table 4. SIC-LDPC and SIC-Turbo BER

Transmit Power (in dBm)	SIC-LDPC		SIC-Turbo
	User1	User2	User1	User2
-20	0.368874643874644	0.351709401709402	0.370617755159740	0.347681651116766
-10	0.0895557538155163	0.0842516591534214	0.0868322387156942	0.0802733313498922
0	0.0174680545668332	0.0123506017278955	0.0161296005135662	0.0115706673491253
10	0.00221317767675344	0.000596952671063959	0.00200211759188682	0.000563768740906340
20	0.000128921184968574	2.07997842027786e-05	0.000120447001194391	2.01010889410507e-05

It can be observed that the percentage improvement in the BER from SIC-to-SIC Viterbi is 87.79% for user1. It can be observed that the percentage improvement in the BER from SIC-to-SIC Viterbi is 86.34 % for user2. While the percentage increases in the BER value from SIC to SIC-LDPC is 99.61% for user1 and 99.54% for user2. The performance of the collision resolution has increased by 13% to 14% when joint decoding techniques are used and thus increasing the throughput of the NOMA paradigm. Percentage increase in BER values from SIC to SIC-turbo is 99.63% for user1 and 99.55% for user2.

6.    Conclusions

Separate decoding and sequential interference cancellation (SIC), two well-known techniques, have served as the foundation for our new decoding scheme, which aims to decode the most innovative packets possible. The optimal solution, which is also the most complex and calls for decoder adjustments, was also studied. It involves jointly decoding all colliding packets and then detecting packet pairings. According to simulation data, the proposed system outperforms separate decoding and SIC by a wide margin. Among the algorithms thus used Turbo Encoder is found to be performing better in terms of the BER obtained. When compared to other decoding techniques, using SIC-Turbo resulted in a lower bit error rate (BER). As a result, the NOMA system throughput and QoS can be achieved using SIC-Turbo decoding. The BER obtained from the SIC-Turbo is found to be performing well with an increase of about 14% from the ordinary SIC implementation. The performance of the collision resolution has increased by 13% to 14% when joint decoding techniques are used and thus increasing the throughput of the NOMA paradigm. Further, the novel optimization algorithm can be used over time for increasing the NOMA network's throughput.

Acknowledgements

We would like to give thanks to the School of Electronics and Communication, REVA University, Bangalore granting access to the experiments and LAB Data sets.