Юорига осилган эластик стержен параметрларини анилаш

Кириш. Қобиқланган уруғларни қуритиш ускунасида юқорига осилган эластик стержен параметрларини аниқлаш учун уни юқорида қаттиқ маҳкамланган балка деб қабул қиламиз ва унга Тимошенко балкасининг эгилиш назариясини тадбиқ этиб, сўнгра бизнинг ҳолатимиз учун қўлланиши мумкун бўлган формулаларни аниқлаймиз

Адабиётлар тахлили. C.П. Тимошенко эгилиш назариясини ХХ аср бошида ривожлантирган. Унинг модели силжиш деформацияси ва айланма эгилишни ҳисобга олади. Бу ҳолат тебранишларнинг тўлиқ узунликлари бакла қалинлигига тенг бўлган пайтда қалин балкалар ва балкаларнинг юқори частоталардаги тебранишларни талқин қилишда қўл келади.

Эйлер-Бернуллининг балка эгилиш моделидан фарқли ўлароқ Тимошенко модели ўз ичига қисман иккинчи даражали ҳосилани олган тўртинчи даражали тенгламага олиб келади. Деформация механизмининг ҳисобга олиниши балка мустаҳкамлигини самарали пасайтирада ва статик юк таъсирида катта ўзгаришга олиб келади, ҳамда ўрнатилган тўплам чегара шароитларининг ўз кичик тебранишларини олдиндан аниқлаш имкониятини яратади.

Чегара шароитлар юқори тебранишларда жуда билинади, чунки тебраниш тўлқинлари қисқаради ва қарама-қарши йўналишдаги силжиш кучлари ўртасидаги масофа камаяди.

Агар балка материалининг силжиш моделини чексиз деб олинса ва ҳаракатдаги инерция эффектини ҳисобга олинмаса у ҳолда Тимошенко модели эгилишнинг оддий назариясига айланиб қолди

Натижалар. Бизнинг ҳолат учун эластик стержен юқорига осилган. Уни юқорига қаттиқ маҳкамланган деб қабул қиламиз (1–расм).

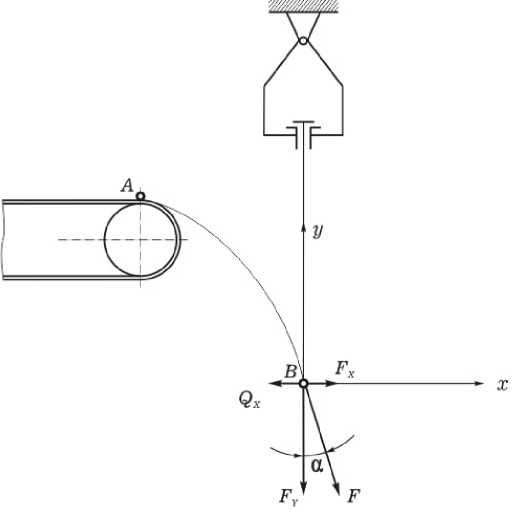
1–расм. Тўқнашувда ҳосил бўладиган кучлар схемаси.

Тўқнашув нуқтасида уруғ массаси оқибатида пайдо бўлган куч эгрилик траекториясининг уринмаси бўйлаб йўналган икки ташкил этувчилардан ибораб бўлади.

Стерженнинг эгилиш схемаси 2–расмда кўрсатилган. Эгри чизиқ билан тугаган варианти Тимошенко вариантидир.

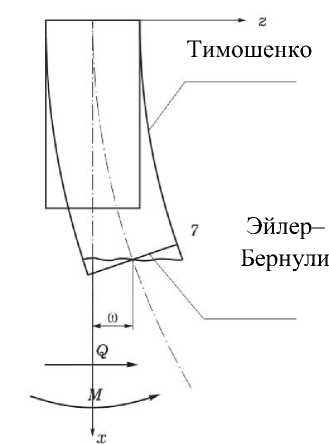
2–расм. Балка деформациясини солиштириш:

Тимошенконинг аниқлашича эгилишда силжиш эмас кесим юзаси текислигининг буралиш бурчаги асосий фактордир (3–расм).

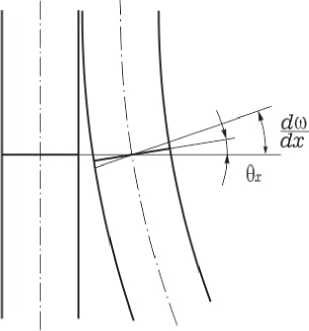
3–расм. Тимошенко бўйича балка деформацияси.

Тимошенко балкасининг деформацияси. Нормал θ_x = φ ( x ) бурчакка буралади у ^{d ω} га тенг эмас.

dx

Балканинг силжиш эффекти қуйидагича берилади.

U x ( x , y , z ) = - z m (x )

Uy ⁽ x , y , z ) = ⁰ U _z ( x , У ) = a (x )

бу ерда x , y , z - балканинг координаталарини белгилайди.

Ux, Uy, Uz - уч йуналишда силжиш векторининг компонентлари Ф - балка урта юзасига нисбатан нормалнинг буралиш бурчаги. о - z у^и буйича юзанинг силжиши бошланFич узаро аълодадар оддий деференциал тенглама:

d (EIdm | = q (x) dx2 I dx ) Ш xx

d a       1 d (   d m А

= m---1 EI I dx      kAG dx у dx J

Тимошенконинг балка эгилиш теоремаси Бернулийникига эквивалентдир, агар охирги купайтувчини х,исобга олмаганда

EI

—-— <  1 булганда бу ядинлашув мос келади. kL AC

Бу ерда:

L - балка узунлиги.

A - балка кесим юзаси

E - эластиклик модули.

K - Тимошенко коэффициенти, юмалод балка учун к = 6/7

q ( x ) - кучнинг тадсимланиши (узунлик бирлигига таъсир этган куч).

I - кесим юзасининг иккинчи моменти.

Бу икки тенгламани комбинация қилсак, бир жинсли бир хил кесим юза учун оламиз:

d4 a          EI d ² q

EI —т = q (x)---k dx 4         kAGdx2

Эгувчи момент М_хх ва силжиш кучи Q_x балкада силжиши ю ва айланиш Ф билан боFлиддир.

Тимошенконинг чизидли эластик балкаси учун бу алодалар дуйидагича кўринишга эга бўлади.

M„ =— EI da ва Q = kAcI xx                               x dx

—

d a m +7Т dx

Бу формулага қуйидаги коэффициентларни киритамиз.

µ А 1 –балка (стерженнинг) осилиб туришини ҳисобга олувчи коэффициент. У осилиб турган қисмидан куч таъсир этган нуқтага бўлган масофага боғлиқ, бу ҳолда зарба кучи бир оз сўнади.

µ_{А 2} –стерженнинг буралишини ҳисобга олувчи коэффициент. Бу ҳолда ҳам зарба кучи бир оз сўнади.

µ А 1, µ А 2 эксперемент йўл билан топилади.

I

У холда                 Qx = Pa1 • ^A2kAG - ^ +I

V

В нукта учун мувозонат тенгламасини ёзамиз;   F_x - Q_x = 0

Бу ердан        Q x = ^Fx .

Бундан ташқари F куч бурчак остида йўналган бўлгани учун Fх куч ишқаланишга дуч келади. Уруғ билан эластик стержен ўртасидаги ишкаланишни уисобга олсак;        Qx = в • Fx

Бу ерда: β – уруғ билан эластик стержен орасидаги ишқаланиш коэффициенти.

Стерженнинг OFирлиги   T_{c т} = A • h_cт • р

Бу ерда:

ρ –стержен материалининг солиштирма оғирлиги г/см ³.

h –стержен узунлиги, м

Кесим юзаси

У ҳолда

A = CT hCT • р

T CT     I       ^{d c}

Qx = вишк ’ PA1 ’ PA 2 • k •-,--G • - V +~P~ hc т ’ P    V      dx

Стержен шарнирда илинганлиги, шарнир атрофида  тебраниш натижасида силжиш катта

улчамга эга булмаслигини уисобга олсак — = 0 dx деб қабул қилсак бўлади.

У уолда            Q x = в ишк • Pa i • ^p A 2 • k • -TC- • G ( — V )

h CT • ^P

Уруғ билан стержен тўқнашув нуқтасидаги кучлар йўналишини уисобга олсак          Qx = Fx = F sin a

Бу ерда: F=m⋅a m–уруғнинг массаси, г.

У ҳолда             ma sin α = β _ишк ⋅ µ _{A 1} ⋅ µ _{A 2} ⋅ k ⋅ ^TCT ⋅ G ⋅ ( - ϕ )

h ⋅ ρ

Бу ерда стержен баландлиги h  = ^{β ишк ⋅ µ A 1 ⋅ µ A 2 ⋅ k ⋅ TCT ⋅ G ⋅ ϕ} .

ma sin α

Бу ерда тезланиш пастга қараб йўналган Y ўқи бўйича, пастга йўналганда Y ўқи бўйича тезлик ошади ва тезланиш содир бўлади

ν _OY - ν _O t

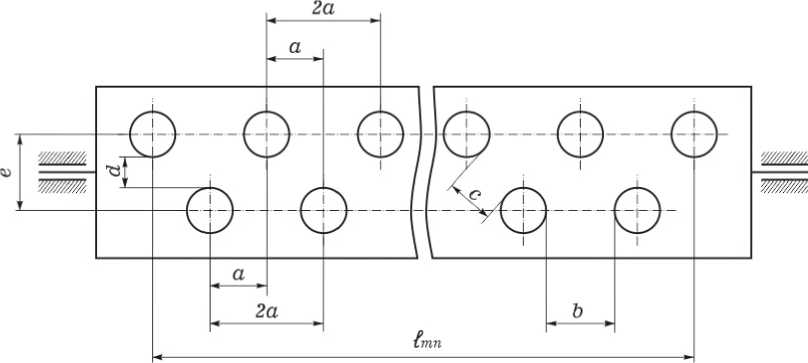
4–расм. Эластик стерженнинг жойлашуви.

Хулоса. Эластик стерженнинг ўрнатилиши 4–расмда кўрсатилган. Стерженларнинг ўрнатилиши шахмат усулида бўлиши керак с , b масофа уруғ размеридан каттароқ бўлиши керак. Қолган ўлчамлар эксперемент орқали топилиши керак.