K-12 Curriculum Research: The Chicken and the Egg of Math-aided ICT Teaching

Published Online January 2017 in MECS DOI: 10.5815/ijmecs.2017.01.01

Being able to handle a computer and the internet is not only the new norm, but nowadays it is a new necessity. Nearly all social and commercial enterprises now conduct their business on-line, and the face-to-face meetings which our parents went through in order to, for example, pay a utility bill or even take out a bank loan are now rare. Our society expects and needs every independent citizen to be able to function on the internet. ICT has become a basic life-skill, and as such it is essential that we incorporate ICT skills into our education system at an early a stage as is practicably possible.

All of this necessitates that our schoolchildren have to be able to use the net with confidence. In order to be able to follow any kind of further education (FE) our schoolleavers have to be able to search for information on the net instead of an encyclopedia. Nearly all students have to consult e-books and e-articles, which can be ordered at low cost, or are even free to read online, unlike in the ‘old days’ when a student’s budget for buying study books often exceeded their budget for food.

Much has been made of the negative social effects of the net, but encouraging our future citizens to utilize the net, and giving them all the skills to do so could actually have significant social benefits, let alone the economic ones. People who can use Instagram or Pinterest to store their favorite pictures can meet like-minded people (albeit virtually), which can encourage them to expand their interests and form bonds with others. The same is true for researchers, i.e. Google Scholar, Mendeley and RefWorks are not only used to search for and store interesting articles for further reading, but they can also lead researchers to establish contact with other researchers, which gives another facet to the concept of networking.

The demand for an expansion of ICT education at all levels of the FNC is clear [1]. The gradual immersion of ICT in all areas of society and the need to facilitate new innovation and productivity require this [7]. We currently have a shortage of skilled manpower to fill the employment needs of our burgeoning ICT industry, so we need to immerse ICT into all areas of society in order bring about a new era of innovation and productivity. Two recently published UK House of Commons’ reports, The Digital Skills Crisis [8] and The Digital Skills Gap [18] in fact quantified the cost of the shortage of skilled ICT personnel by stating that the digital skills gap costs the British economy £63 billion a year in lost GDP.

In the U.S., the act ‘No Child Left Behind’ (NCLB) was continued in 2015 by the renewed congress bill ‘Every Student Succeeds Act’ (ESSA). Its goal is to leverage the affordability and quality of education, especially in STEM subjects. The acts stipulate the necessity of improving access to the wealth of freely available information which the net has given us by equipping schools with up-to-date ICT devices, highspeed connections and with 100,000 highly-trained new STEM teachers. In accordance, the STEM education coalition is advocating STEM education as a national priority. The economic justification for this is summarized in its one-pager [37] that states, for instance, that “ 60 percent of U.S. employers have difficulties finding qualified workers to fill vacancies in their companies ”, and ” Jobs in computer systems design and related services – a field dependent on high-level math and problem-solving skills – are projected to grow 45 percent between 2008 and 2018 ”.

In Finland, the strategy for the development of the information society 2007-2015 emphasizes good ICT-skills for accessing services, for increasing overall productivity and for renewal. However, our industrial base is currently going through a period of upheaval as it adapts to the stagnation of economy caused by the fall in Nokia’s market share, and turmoil in the paper industry. This has led to structural changes in the nature of our economy, and in some cases, to massive layoffs of skilled ICT personnel as well. Because we currently have this pool of unemployed ICT-trained personnel there is certain reluctance on the part of our economic planners to increase the provision of ICT. Rather, the National Digital Agenda of 2011-2020 emphasizes of the societal impact of ICT, such as organizing public services for improving sustainability, transparency and civic participation, where social networking contributes to strengthening the dialogue between the public and private sector. According to this agenda, ICT should be an integral part of education. From the earliest age, well-designed digital services and learning materials (e.g. games and simulations) should be developed and deployed, and distance learning options should be provided for students living in remote areas.

In addition to individual countries setting out their own policies for the promulgation of ICT, several international coalitions and organizations, such as the EU and the OECD, have stressed the importance of ICT education. The EU states that shortages of e-skills in the European workforce will result in an excess demand for ICT practitioners. In their recent visionary reports in 2016, European Committee foresaw the Digital Single Market (DSM) growing to its full potential. This would be based on common ICT standards and initiatives, such as the eGovernment Action Plan, the European Cloud Initiative, Public Private Partnerships and the Fourth Industrial Revolution. This revolution will utilize the potential of integrated cyber-physical systems and technologies in which Finnish research and industry is already leading the way. We must equip our future workforce with the skills and confidence to operate in the world of big data and the Internet of Things. Although the EU has facilitated the growth of ICT education by funding research with its Horizon 2020 programs, many EU countries lag behind these initiatives and increasing differences in ICT skills are slowing down the development of EU-wide standards and procedures. For example, as the administrator of the EU-wide PISA tests, the OECD is in a unique vantage point for reviewing the education systems of various countries. In this context, it is worth noting that the OECD’s recent report [28] makes it abundantly clear that all students first need to be equipped with basic literacy and numeracy skills in order to be able to participate fully in the hyper-connected, digitized societies of the 21st century.

This article is not only concerned with showing the importance of teaching ICT in schools, but also aims to show the importance of ICT for all members of society. Therefore, we first examine the relevant pedagogical literature aimed at justifying combining ICT with math, as this is the approach currently favored by the Finnish education authorities for the (new) Finnish curriculum. The idea is to teach ICT as a cross-curricular subject, starting with building hands-on assembly kits and electronic experiments in craft subjects at the primary school level. However, the bulk of the ICT syllabus will be integrated with math. Therefore, the initial and primary ICT learning goals, i.e. the generic requirements for algorithmic thinking and the ability to write simple command sequences, are inserted into the math syllabus.

In the following chapters we will go through the ICT and math syllabi in more detail, viewing their potential as a combined syllabus, and as separate ones. In the Results chapter, we will evaluate and compare the two approaches, either math-aided ICT or ICT as a separate subject. This paper’s contribution to the field of curriculum research is its focus on the differences between the reviewed math and ICT syllabi. The paper highlights the expected benefits of each approach to teaching ICT, taking into account not only the knowledge gained from academic research, but also ICT curriculums of other countries. The paper concludes with a summary of our findings and some recommendations for the future.

• A. Research Question

This study asks:

• •    How does ICT fit in with the mathematics curriculum?

• •    What are the fundamental concepts of computer science, and how do they interact with the corresponding concepts of math?

• •    What ICT topics are left uncovered in the current FNC, when compared with the discrete computing curriculum of the UKNC?

• II.   Related Work: Pedagogical Considerations

From the pedagogical standpoint, combining math and ICT is well justified and can be expected to have a positive effect on the learning of both subjects. The following sections will describe the links between ICT and math in terms of transfer, explicit abstraction, and the areas in which ICT can be used as a scaffold for learning math skills, and vice versa.

• A.    Transfer of Learning

Transfer of learning is based on the principle of transferring a skill from one domain to another [36], in our case from math to ICT and vice versa. Learning Transfer explains why learning by analogy is easy. For example, the driver of a car has many of the skills needed to drive a truck, although jumping into the cockpit of an airplane would still be quite a challenge. Successful transfer correlates closely with the current level of acquired expertise: the greater the expertise, the more flexible are one’s mental models for adopting new knowledge. An expert finds correspondences and analogies by exploiting previously constructed schemas, identifies without extraneous effort the significant features of new material and hence learns easily in new situations, whereas a novice is stuck with the amount of data and concentrates on irrelevancies. According to venerated model building theories, such as Piaget’s genetic epistemology [31], learning is perceived as modifications to the existing schemata; termed as assimilations, if little or no reorganizing is needed, and as accommodations, if the existing schema needs reconstruction. In defining the concept of expertise, Gestalt psychologists (e.g. [21]) refer to the insight experience that helps one find the right solutions intuitively and enables the subject to predict outcomes in new situations.

Transfer may occur either laterally or vertically [17], implying hierarchical learning steps. Transfer can also be near or far [30] within one nearest domain or extended to other further domains. Lateral transfer is more likely to occur and quicker to perform than vertical. Transfer which occurs at only one level is lateral. For example, in math, stepping from addition to subtraction only involves a small cognitive gap, whereas jumping to reordering the equation is a significant step. In pedagogic terms, one level is called a “learning set”, and proper and robust learning means progressing consistently from one level to another. Stepping to the next level requires complete mastery of the previous level, in which case, the subsequent vertical transfer can be made without too much difficulty. If sudden vertical jumps are made in learning, however, the variation in learning outcomes among the students grows, and poorer students will suffer.

There are two options for fostering successful learning transfer, and they have been described as the low road and the high road of education. The low road prescribes strengthening routines by iteration, as a result of which responses develop to become more reflexive and automatic. The high road means mindful and explicit abstraction and an active search for connections [30]. In teaching and learning, this requires that teachers should explicate the underlying principles and point out connections to prior knowledge. As for the learners, they should become more aware of concepts, their relations, and ultimately, they should metacognitively recognize the necessity of making associations in order to enable deeper learning. Nowadays, in Finland at least, explicit abstraction is the accepted approach to mindful, conceptual elaboration which fosters learning transfer.

Transfer has been studied in the context of learning new languages. As a base language, the usefulness of teaching Latin is recognized. In addition to the positive correlation between knowing Latin and learning Romance languages [19][35], the favorable effect also applies to learning other, linguistically unconnected languages. This shows that if learning transfer is successful, a student is capable of finding the common underlying conceptual basis of different topics [17]. Finding such analogies requires a certain level of intellectual maturity at which the student is able to elaborate the material conceptually in order to reach a deeper understanding. In this respect, a positive correlation between ICT and mathematics does appear to exist, so learning transfer is a central theoretical concept of this study.

• 1)    Transfer between ICT and Math

The transfer of learning between languages is analogous to that of math and ICT. As Dijkstra [10] claims, ‘Programming is one of the most difficult branches of applied mathematics’ . Syslo and Kwiatkowska [38] argue that discrete mathematics is central in developing algorithmic thinking, which is one of the key skills in ICT, whereas Flatt in the panel discussion [42] states that, in fact, programming is an extension of algebra. It has long been recognized that good math skills are helpful in learning ICT. Conversely, ICT is known to benefit algebraic, logic and problemsolving skills needed in math. The transfer from ICT to math is straightforward. For example, a student trying to master the basic concepts of function and variable in algebra, would be helped if he can practice with an interactive ‘shell’ or programming environment and writing small programs. On a larger scale, programming means solving problems by dividing them into smaller solvable elements, often implemented as functions, which is similar to problem-solving in math.

Hello World! Usually, becoming acquainted with a programming language is begun with this brisk greeting: a programmer calls the simple print function and the computer shows the greeting on the screen. One can still obtain a lot of information from this short first meeting, such as, whether the main() function was needed, how parameters were given, how commands were finished, whether indents were needed, how errors were communicated to the coder etc. “Hello World!” is also representative in illustrating the very fundamentals of coding. In most languages, the command drawing the text on the screen, i.e. print(), is a built-in function that is called with a text string as a parameter. The parameter is handled as an anonymous variable instantiated for the duration of the function call, after which it is passed to the function and then destroyed. Even if it is not apparent, passing a string parameter gives the first glimpse of a variable. Meeting the profoundest programming fundamentals, the function and the variable, even in the simplest test program, is an achievement that underlines the importance of these two concepts. Coincidentally, they happen to be the basic concepts of algebra as well. In the section Variables and functions as common fundamentals, we analyze their importance in more detail.

Hello Algebra! Among the syllabus areas, students struggle most with algebra and functions [23]. Instead of plainly giving an answer to a problem, a student should examine the properties of a function, such as gradients, maxima and minima. Progressing gracefully anticipates a shift of paradigms from the arithmetic to algebraic. In algebra, not only is the concept of a function causing problems, but also getting the variable is difficult. As a surrogate concept, the unknown is used as a bridge in order to learn the concept of the variable. At primary level, the unknown, often represented as a gray box, question mark or an empty space in a calculation, is at secondary level replaced with ‘ x ’. However, the unknown unlike the variable, is understood as a static value, which does not change after it has been figured out. The relation of x and y , i.e., a function y = f(x) , and analyzing its properties both algebraically and graphically, is the new core. With a function “machine” each input of a new x value will produce one (and only one) output value of y .

Multiple representations serve as a cognitive aid to learning by providing a means to switch the point of view. Functional thinking can be defined as a type of finding a relation between two varying quantities; hence it has its applications in science, especially physics, the core of which is to depict the laws of nature. Rakes et al [33] have studied the challenges of developing the algebraic thinking, and they have found that especially symbolic notations and abstract reasoning are causing problems, and that students think that they are not properly prepared for making the headway in abstract thinking and generalizations. Rakes recommends conceptual instead of procedural learning for the sake of better transferability that would result in more flexible learning.

Wilkie [44][45][46] discusses the challenges of functional thinking and promotes gradual development by using multiple presentations and bridging arithmetic and procedural knowledge more cautiously. For the primary school, Wilkie has illustrated a pathway of generalizations of sequences as a preparation for algebra; these exercises are labelled pre-algebraic. Development steps include figuring out patterns out of geometric sequences, growing these patterns by defining next items, and visualizing the increase of amounts. In generalizations, it is important to gradually grow recursively step-by-step to defining the nth term that determines the relation and general solution. In sequences n implicitly represents a variable. In addition, Wilkie emphasizes the linguistic means of describing problems by using pronumerals. By a pronumeral she means the verbose name of a variable in contrast to one letter notation allowed in math. The pronumeral may be called, for instance, number_of_tiles. This kind of naming complies with ICT coding conventions. In addition to textual representation, also the visual representation provides a beneficial view of the function. The graph gives lots of information for finding the solutions and about the behavior of the function, e.g., the maxima and minima. In addition, the general knowledge of polynomials (continuity, the dominance of the greatest degree) and rational functions (optional discontinuities and asymptotes) helps in depicting the nature of the function.

• 2)    Transfer between ICT and other subjects

Deep as the linkage between math and ICT might be, the rigorous mastery of one’s mother tongue is a prerequisite for graceful performance in academics overall. Similarly, reading disability predicts disabilities in other subjects and in math, and in the light of this comorbidity, poor performance in ICT is to be expected [47]. In addition to the one’s mother tongue, knowledge of the English that constitutes the base for computer languages is an advantage.

The logic of a sentence in verse is to be parsed before understanding algebraic notations in symbols. Philosophers dating back to Aristotle have regarded language as the source of logic and creativity. The task of education would thus be to stimulate all the faculties and nourish young minds. In addition to logic contained in one sentence, constructing a plot or chain of arguments in factual writings should form a logical path. At some point, logic has been taught as part of the optional subject of philosophy - however, logic overlaps also with language and math. As a scaffold of improving logic, a teacher could introduce new tools, such as argument mapping [9], which belongs to the same mapping family together with mind maps and concept maps.

Modeling and abstraction skills are beneficial for ‘learning to learn’ purposes. In studying academic subjects, concept mapping might become a handy tool. Strengthening conceptual learning is never a waste of time. In general, study skills are worth investing in: knowledge can change and things tend to be easily forgotten, but study skills remain. Metacognitive skills refer to a student's awareness of his means of learning and allow him to plan good strategies for learning, which implies that a student possesses strategies to choose from, such as concept mapping. However, learning to learn should be a cross-curricular goal involving all academic subjects.

• B.    The fittest programming paradigm

From the three most prominent paradigms of imperative, functional, and object-oriented, the imperative paradigm is often considered the simplest, based on easy-to-explain concepts and a low level of abstraction. Also, it is easy to visualize with the help of control flow diagrams. Some traditional programming languages, such as Basic, FORTRAN and C, are examples of an imperative paradigm, and command shell scripts employ this paradigm, too. C is by far the most popular imperative language today. However, because it is a low-level language, it allows direct access to HW resources, such as memory and sensors, which forces the programmer to pay a lot of attention to memory management. This raises the pitfalls of handling memory, which is why low-level languages are far from simple for beginners.

Especially in the early history of ICT, imperative paradigm was appropriate, since program instructions were executed in a sequence and the end result was predictable. Functional paradigm and languages were being developed in parallel, however. With the advent of graphical user interfaces (Mac, Windows), the event-driven model started to change mainstream programming. The imperative programming paradigm was enhanced with classes and objects resulting in object-oriented paradigm (OOP) that was especially fit for bigger systems. Then the web took over the world and programming paradigms had to adapt to that. The event-driven model of programming was extended to web applications. Well-defined and often strict programming languages were gradually substituted by the looseness of internet languages, such as HTML, JavaScript and PHP, and finally with all sorts of tag-based extensions (such as JSP and ASP) mixing static and dynamic web content at will. The latest developments are transferring JavaScriptbased technologies also to the server (Node.js). Thus, the worst nightmares of programming purists have become true.

The programming paradigm should support the desired style of writing code. While advancing in skills, a student is expected to internalize good coding conventions, such as modularity, documenting, testing, and, in the later stages of studies, also saving HW resources or speeding up response times. Modularity is achieved by splitting the system into suitable structural components, which can be done at different levels in different programming paradigms. In the OOP, the system is constructed by interfaces and classes, the relations of which may comply with design patterns (such as Visitor, Strategy). In modelling such a system, UML class diagrams are often used. Classes define member variables and methods (functions) and hence encapsulate that class related data.

In regards to transfer between math and ICT, i.e., in bridging algebra and programming, lambda calculus is the missing link [36]. In its conciseness and execution of algebraic operations, such as reductions, lambda calculus conforms to the symbolic expression characteristic of math. It is also categorized as a functional language.

Since it possesses the highest purity and hence a special added value in pedagogy, it appeals to ICT teachers and theoreticians. In addition, being applicable in proving and other theoretical studies in ICT, the lambda calculus and its pure derivatives are willingly used as an introductory university course for functional languages. As the first language in the primary and secondary school, lambda calculus is definitely overkill.

Regarding the functional programming paradigm, the complexity issues have been addressed in educational initiatives targeting at primary and secondary levels. The functional programming camp has tried to satisfy the wishes of ICT educators and provided suitable courses and material: WeScheme, TeachScheme!, Logo Turtles to practice algorithms [16] for example, and DrRacket and also Bootstrap which uses the Racket programming language (prev. PLT Scheme) [23][24][36]. The Bootstrap course targets ultimately at game design. In using Bootstrap, promising results among K-12 students have been reached, Felleisen and Krishnamurthi [13] state boldly that “ Bootstrap provides the strongest evidence yet that teaching functional programming directly affects the mathematics skills and interests of K-12 students ”, and along with them researchers have long regarded programming as a mightifier in learning mathematical concepts (e.g. [35]). Moreover, Schanzer [36] highlights the low threshold of transfer, “ Bootstrap uses algebra as the vehicle for creating images and animations. That means that concepts students encounter in Bootstrap behave exactly the same way that they do in math class. This lets students experiment with algebraic concepts by writing functions. ”

Levy [24] implemented the Racket course for elementary mathematics teachers by adding the consecutive principles of algebra of images and targeting good coding conventions and discipline through using test-first design and documentation. Algebra of images uses images as variables in function calls and prepares for mathematical variables and functions in an entertaining and creative way.

Complexity-wise OOP sets a certain threshold for learning as well. Inheritance, polymorphism and virtual functions, for example, are regarded to belong to the Top-10 most difficult items [27] . Object oriented paradigm is an extension of the type concept found in procedural programming languages. Furthermore, it is hard to understand methods without first understanding functions. Therefore, OO-paradigm is not appropriate as a first programming paradigm. However, some visual programming tools, for example Scratch may be interpreted as object-oriented, after which the paradigm is not complex at all. Got this way, sprites are objects, whose methods and events are defined, as well as variables set by dragging and dropping.

• C.    BYOD (Bring-Your-Own-Device) and forget not to BYOB (Bring-Your-Own-Brains)

Teaching mathematics in Finland is in a transitional stage due to the use of symbolic calculators (allowed since 2012), and shortly also computers, in the matriculation examination. Symbolic calculators bring an excessive competitive advantage to their users. In the spring of 2016, the exam was split in two parts: run with and without a calculator, and the gain of having a symbolic calculator was compensated by making some problems more difficult. In the spring of 2019, the math exam will become electronic as last of the exams. The applications allowed at the work station are the following: LibreOffice for text editing, spreadsheets, vector graphic, GIMP, Pinta, InkScape, Dia, wxMaxima, Texas Instruments N-spire, Casio ClassPad Manager, Geogebra and LoggerPro [49]. Especially scriptable tools are interesting in regard to ICT teaching.

According to the Finnish curriculum 2016, calculators and computers are first to be familiarized with during Y3-Y6. In Y7-Y9, they are applied as learning, assessment and creativity tools. Regarding function keys, the first math concepts are squaring operation x² and powers of 10 (e.g. when typing a standard format), since powers and indexes are taught in Year 7. If we consider the squaring operation x² as a function, x is a variable or a function parameter. The user enters the value of x, after which the calculator prints the value of the function ( f(x) = x² ) on the screen. Does the student understand that he is using a function? It is unlikely, if this is not especially emphasized, otherwise its meaning is simply reduced as an action button. By pressing it a student gets the desired result, a number squared, as a procedural outcome.

The affordances provided by calculators could be exposed and the function behavior explicated, e.g., the teacher could point out the existing function key f(x), and as a concrete example demonstrate the use of the simple function of x2, first assign the x value and retrieve the value of y as the end result of squaring. As a visual hint, the point (x, y) could be positioned to the coordinate plane. By inputting sequential integers (1, 2, 3 …) and plotting points to the plane, the quadratic curve starts to be recognizable. The same exercise may be reused to deduct next numbers of the quadratic sequence. Visualizations of functions with the calculator are beneficial as multiple representations without additional computational overhead. For instance, Desmos as an online tool and Mathematica, Maxima and Maple as installable ones are handy in building and exploring functions. However, neither calculators, nor tools nor games are necessary in teaching mathematics. Actually, adapting to the use of a certain device implies a risk of conceptual welding [35], after which a user is not capable of fully functioning without the device. Expediently, a calculator should remain an optional tool and not a necessity.

Not even learning ICT requires using computers. Many complementing skills necessary in ICT may be practiced well without them, such as computational thinking (CT). Abstraction is one of the three ‘a’s of computational thinking according to Jeannette Wing [48], who launched the term. The remaining ‘a’s are automation and analysis. As Wing puts it, “ Computer science is not only computer programming. Thinking like a computer scientist means more than being able to program a computer. It requires thinking at multiple levels of abstraction. ” Abstracting systems may be sharpened with mind mapping / concept mapping exercises; in particular, tighter-syntax concept mapping approaches the UML class diagrams used extensively in OOP system design in the industry. Automation, in turn, merges mastering control structures, divide-and-conquer of the problem domain and finding the right algorithms [22].

• III.    Results

In order to facilitate comparisons, the ICT syllabi of FNC and UKNC are illustrated as concept maps. As maps, the approaches of math-aided ICT versus ICT as a separate subject are more easily comparable. We first focus on the computational thinking that is common for both syllabi, and after that evaluate the importance of areas that are omitted from math-aided ICT compared to the dedicated ICT syllabus.

• A.    Math-aided ICT teaching

Mathematics as a subject is constructed based on spiral progress to more advanced topics. The iterative visits at each math topic at different levels will deepen the knowledge and add details. In merging ICT with math, it is justified to follow the well-established order of math and include corresponding ICT topics where feasible. We took the Finnish math syllabus as the basis, and Figure 1 demonstrates how mathematics as a subject is constructed chronologically and how it expands in a cyclic manner. The concentric gray circles demonstrate different school levels from primary to high school. The further away the subject is located from the center, the later it will be introduced. The figure appears to divide the math syllabus into four major subject areas: arithmetic, geometry, algebra, and the newest addition, computational thinking (CT). CT will lead students to learn how to decompose and solve problems by dividing them into smaller sub-problems, as well as algorithms and modelling.

The Red parts represent topics that are considered especially opportune for ICT teaching: the darker the color, the stronger the emphasis. In addition to CT (algorithms, logic, modelling), the variables and functions of algebra are marked in deep red. Topics marked with lighter red are optional, and proposed as nice-to-have features. For instance, statistics and probability could lead students towards the fields of data visualizations and data science. In addition to these red-scale areas, the reader should note the UK and US flags. The Flags represent those math additions that are missing from FNC but present in UKNC or USCC, and are anticipated to prepare the students for ICT. Such key areas include sets and matrices. Interestingly, USCC explicitly also defines modeling as one syllabus area that is helpful for both math and ICT.

• 1)    Logic, sets and matrices

The initial “hello worlds”, programming evolves into writing control structures such as if-then-else sentences and loops. An if-sentence requires the truth value of its condition to be evaluated, thus presuming skills such as propositional and Boolean logic. The same skill applies in handling iterations when reaching the loop termination condition – typically an equivalence or end of an inequality. These are just the simplest cases where logic in programming is needed. Logic primitives, including truth values as computational entities, seem to be missing in every math syllabus. However, in the UKNC, Boolean logic is currently included in the computing curriculum [3]. Considering the importance of logic to all computer science, this is a distinct lack. The basics of logic, including Boolean logic (true, false, AND, OR, NOT) could very well be included in the math syllabus.

When the amount of data increases, bigger data stores are needed as instead of single variables arrays and other collection types will be introduced. The set is the basic mathematical construct for containment. Sets are highly relevant for programming, as they are the basis for abstract data types called collections and the relational database, among other things. An array may be introduced as a set, a vector or a matrix, and the same operations apply. Therefore, set theory would be useful in any mathematics curriculum designed to support ICT and programming. Currently, set theory is part of UKNC, but is absent from USCC and FNC.

Linear algebra is included in the USCC as matrices and as the syllabus domain of vectors and transformations in UKNC, but matrices and transformations are missing from the FNC. We consider it important for computer science, as matrices enable easy manipulation of data and often simplify computational logic. Matrices are extensively exploited, e.g. for 2D- and 3Dtransformations in game development and in data analysis and pattern recognition.

All suggested new math syllabus areas remain at the preliminary level in UKNC and USCC and we propose the same: in logic truth tables and Boolean logic in order to simplify several simultaneous conditions; in sets, Venn diagrams and basic operations of union, intersection and cut with at most three sets; and in matrices, transformations of translation, reflection, rotation and enlargement and finding an inverse matrix. This new math knowledge should be carefully bridged with the prior knowledge with lots of visual exercises and by starting early enough.

Table 1 illustrates in which order these topics, logic, sets and matrices are handled in the UKNC and the USCC.

Table 1. Math syllabi of uknc and uscc

	UKNC	USCC
Logic	(in Computing Syllabus) KS2 : logical reasoning to explain how simple algorithms work KS3 : simple Boolean logic (AND/OR/NOT) and its applications in circuits and programming	-
Sets	KS3 : enumerate sets, unions/intersections, tables, grids and Venn diagrams KS4 : data sets from empirical distributions, identifying clusters, peaks, gaps and symmetry, expected frequencies with two-way tables, tree diagrams and Venn diagrams	G6 : data sets, identifying clusters, peaks, gaps, symmetry G7 : random sampling to generate data sets HS : interpret differences in shape, center and spread of distribution
Matrices	KS4 : (in Geometry) translations as 2D vectors, addition and subtraction of vectors, multiplying with a scalar, diagrammatic and column representations GCSE: Transformations & Vectors	HS : add, subtract, multiply matrices, multiply with a scalar, identity matrix, transformations as 2x2 matrices

• B.    ICT as a separate subject

Instead of teaching ICT together with math, it can be taught as a separate subject, as has been shown by the way computing is taught in the UKNC. The computing syllabus was reviewed to discover uncovered topics of the math-aided approach to FNC, see the blue nodes in Figure 2. The Red nodes illustrate overlapping topics found both in UKNC and FNC, where the allencompassing skill of computational thinking that consists of such sub-domains as algorithms, logic, problem-solving and abstraction is well represented. Algorithms and problem-solving start from the very beginning, whereas abstraction and modelling is from Key Stage 3 upwards in the form of pseudo-coding and flow charts, for instance. Modularity as a good coding practice is highlighted.

In addition to computational thinking, the thread of security and safety starts already from Key Stage 1 and deepens throughout the different stages. In UKNC Computing, safety and security areas culminate as cyber security e.g. identifying possible attack types and system vulnerabilities. The safety and security domain includes the ethics aspect covering a person’s own behavior regarding his own and others’ privacy and covering respect issues as well.

In Key Stages 1 and 2 of the UKNC Computing, the subject content is divided into two parts, first ICT from the perspective of a user and secondly of a programmer. In the user part, the fluent use of technology aims at storing and manipulating digital content. The goal is to understand the digital nature of stored media, text, music, videos. In Key Stage 2, networks are included and their properties, e.g. types and connectivity, are studied. From the perspective of programming, new control structures, sequences and repetition are introduced, as well as such fundamentals as variables and I/O.

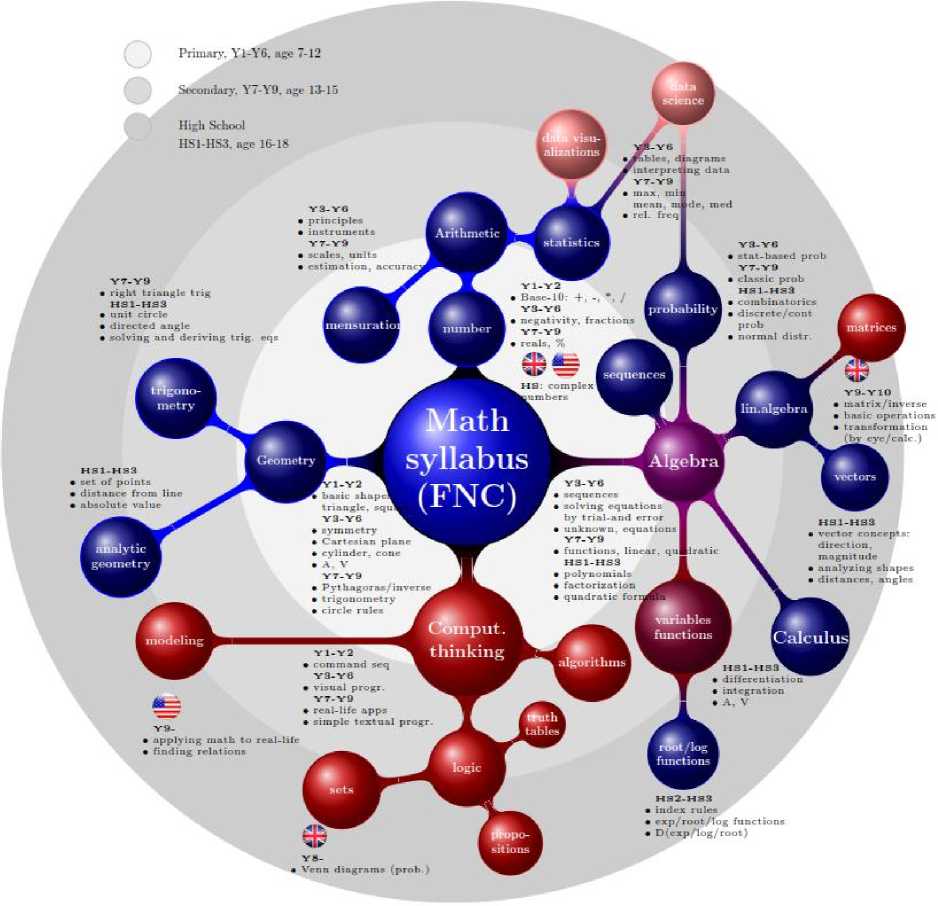
Fig.1. Combined Math syllabus, based on FNC with additions, computing related items in shades of red, additions from UKNC marked with

and from USCC with

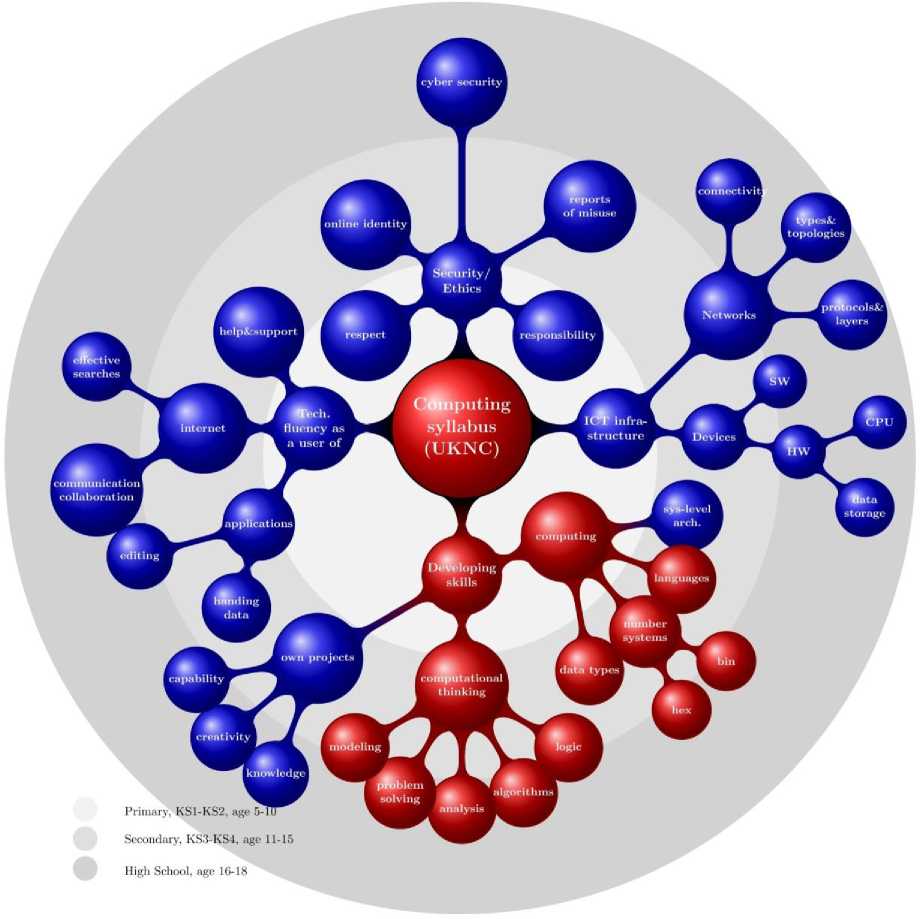
Fig.2. ICT as a separate subject based on UKNC. The parts that are overlapping with the UKNC and FNC syllabi are marked in red, uncovered items in blue.

From Key Stage 3 onwards, new data structures such as lists, tables and arrays will strengthen the programming skills. Boolean logic (AND, OR, NOT) is brought in and students are familiarized with the binary presentation. Computer systems are reviewed more in depth by introducing HW and SW components and various storages, and the way in which data is stored in memory. In Key Stage 4, the skills are strengthened and analytic thinking and creativity are fostered and applied to one’s own interests [4][5]. Students may implement e.g. small applications, portfolios or hypermedia e-books [32] and hence provide material for assessment.

Learning algorithmic and computational thinking is considered as part of mathematics education in FNC as well. On the other hand, issues such as computer and internet architecture, internet of things, robots, big data, cloud computing, artificial intelligence, augmented reality, social media and data privacy and security, are currently omitted. In addition to possible mathematical aspects, these issues involve technical, psychological, societal and legal viewpoints, among others. As Facebook, Twitter, Angry Birds and Pokémon Go phenomena have demonstrated, we live in a world where new ICT inventions can very rapidly take over the whole world -and it would be irresponsible not to give our pupils and students necessary skills to survive in this technological era of wonders. Fluck et al. [14] argue, "Computer science is rapidly becoming critical for generating new knowledge, and should be taught as a distinct subject or content area, especially in secondary schools".

• C.    Variables and functions as common fundamentals

In this section, we analyze the variable and function concepts in more detail. Variables and functions are the very heart of modern mathematics and science. According to Menger [26], in the development of mathematics and natural science, perhaps the most characteristic concept is that of a variable. Tarski [39]

states that the invention of variables constitutes a turning point in the history of mathematics. Kleiner [20] sees the function concept as a distinguishing feature of modern mathematics. In computer science, variables and functions have been an essential part of programming from the very beginning. As computing necessarily involves computer memory, a symbolic reference to a memory location, i.e. variable, is a necessity. Functions were also introduced very early: the second FORTRAN implementation (Fortran II, 1958) already included them. Since then, functions have been part of all major programming languages and have had a major role in various programming paradigms, such as structured programming, procedural programming, and functional programming. Function is the basic means of software decomposition [29], a generally accepted software engineering practice. It directly supports the principles of separation of concerns [11], information hiding, encapsulation and software reuse.

Variables are usually introduced in school mathematics long before functions, e.g. according to the Common Core standard, variables are presented at grade 6 and functions at grade 8. Table 2 summarizes the differences of variable in school mathematics and in programming. To link variable in math and ICT, Epp [12] advises instructors to draw analogies.

Table 2. Variable in math vs. ICT

	Math	ICT
use case	unknown in equation, a general number, assignment	“bucket”/ memory store, assignment, scope: global/local
alt. use case	function parameter	function parameter passed by value or reference
type of variable	typically numeric (integer, fraction, real number)	numeric or more complex type

Table 3. Function in math vs. ICT

	Math	ICT
description	relationship between two quantities (usually x and y) or between elements of two sets	a subroutine that calculates a return value based on input parameters or accomplishes a specific task
number of parameters	typically 1 in elementary math and increasing in advanced math	0 ... n
type of parameters	typically real numbers	numeric or more complex types
number of return values	1	typically 1 (0 ... n depending on language)
return type	typically real number	numeric or more complex type

Tables 2 and 3 illustrate the interconnectedness of the function and the variable in mathematics and ICT. Especially in ICT, functions and variables are hard to separate from each other - you need both at the very early stage. If functions in mathematics were introduced earlier, together with variables, the mathematical function concept could be used as a starting point for introducing functions in programming languages. Furthermore, the student probably uses some form of calculators, which typically exhibit quite strongly the concept of function in their interface.

In analyzing the concepts of variable and function, different meanings were discovered. For example, the model of three uses of variable [41] lists variable as an unknown, a general number, and mutable value of x in a functional relationship. As unknown, once the value is solved, no reassignment is usually done, so variable is understood as a constant. When the process of generalizing begins, a student starts to transfer from arithmetic towards algebra by identifying patterns [40], e.g. Wilkie [44] uses sequences to facilitate using variables as a pattern generalizer in identifying functional relations. The general number is a midway to actual variables, which are full-blown in functions illustrating the interplay as a relation of the two, x and y .

Furthermore, in formulae, the location and naming of the variables define the identity either parametric as a coefficient (constants) or variable as an unknown, for example:

f (x, y, z) = ax2 + by3 + cz + d (1)

a , b and c are understood as parameters or general numbers, whereas x , y and z are actual variables.

By the mathematical definition of a function, the ambiguity of output values is not allowed i.e. a function results only one output value per each input. In addition, a domain must include only such input values that produce an output. In programming, the ambiguity of a variable creates confusion. The variable is not its value only, but also comprises a physical location. The address of the variable in a memory is called a pointer in ICT vocabulary. Variable x is referenced by a pointer p , see Figure 3, and these two representations are interchangeable by using certain operations. In the following, we use the C-language notations.

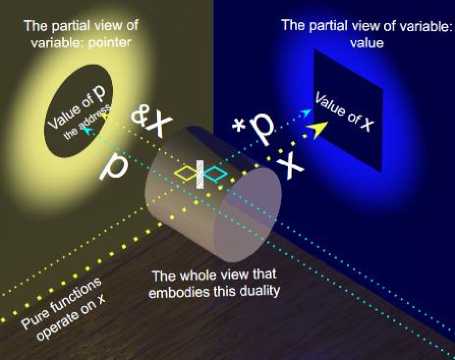
Fig.3. The duality of variable x and pointer of p

Note the operators &, which is the address-of, and *, which is the dereferencing operator. Even if you are using variable x , by adding ‘&’ in front, the address of the variable will be exposed. Analogically, the reference p may be de-referenced to get hold of the value of x . Related memory aspect is the data type of the variable influencing the space reserved. For an unsigned integer the space requirement is much less than for a decimal number ( float , long ). When declared, variable and pointer are not necessarily assigned a value. In lower level languages, for example in strongly-typed C language, the user is responsible for allocating the memory ( malloc ) of the required data type for the pointer p , for example:

int *p;

p = (int *)malloc(sizeof(int));

an operation, which is often forgotten. Both the value and the address may be changed later: a value may be reassigned and the pointer may be redirected to another location. Without special caution, these changes and their side effects may be subtle, go unnoticed and cause nasty and hard-to-trace error situations. Pointers and dynamic memory allocations are among of the hardest ICT topics [27]. In order to fully grasp the concept of variable, unveiling underneath HW structures, i.e., a memory stack, is necessary. Figure 4 demonstrates that in UKNC at the GCSE level, book publishers do not hesitate.

The following code will set up three variables. The variable names, pointers, memory locations and values in RAM are shown on the right as they would be at the end of the three lines of code running.

[ playerKame = "Tony"

■ playerScore = 0

। numberOfEnemies = 7

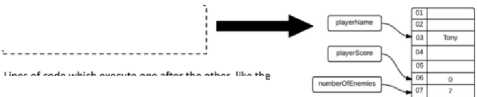
• playerScore ■ 10

Lines of code which execute one after the other, like the above program, are known as a sequence.

If the following assignment were made to playerScore then the value 0 in memory would become replaced by 10.

Fig.4. The GCSE book illustrating variable and its address [15]

Similarly, the concept of function is multifaceted and depends on the used programming paradigm; see the summary of both fundamentals below, in Table 4.

Table 4. Variables and functions in selected programming paradigms

	Variable	Function
Imperative	Global and local variables. Pointers exploited in code (in some languages)	Function (returns a value) Procedure (no return value) both may cause side effects
Functional	Variables as constants or unknowns. Once assigned a value is not meant to be changed	Both pure and impure implementations that rely heavily on recursion, sequences and algebraic manipulation
OOP	Member variables encapsulate data inside the object, visibility controlled by access modifiers (private, protected, public)	Object methods that need an instance vs. static methods that need not. Parameters may be passed by value (no changes) or by reference (changes)

Math rules may be violated in all other paradigms but pure functional, which has inspired functional programming advocates to promote its use for teaching algebra as well.

In the adjacent Figure 5, the first function illustrates a valid function in the mathematical sense that takes an input and produces a single output. The next two functions do not follow the rules, e.g. the middle case forks in two different result options based on the inner state of the program. The bottommost case illustrates a procedure: in an imperative paradigm subroutines are split into functions and procedures based on whether they return of value or not.

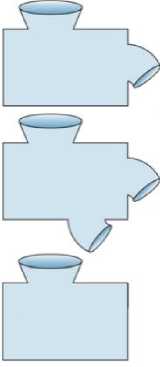
Fig.5. A pure and an impure function and a procedure

• IV.    Conclusions

How does ICT fit in with the mathematics curriculum?

Programming is heavily based on mathematical concepts. It may be seen as problem solving that requires dividing a problem into smaller solvable sub-problems, modelling a solution and applying algorithmic thinking and logic, as in math. Orientation of problem solving and automation is called computational thinking (CT), which is the most recent addition to the Finnish math syllabus in the 2014 edition. In addition to CT, we recognize algebra, linear algebra and set theory as prerequisites for ICT. From different programming paradigms, functional programming has been found to scaffold learning algebra in particular. Thus using e.g. Racket exercises with image algebra will benefit students, as the move from algebraic function and variable to their computational counterparts complies with the near transfer of learning.

As algebra tutors, calculators and other mobile devices should be exploited to their full potential. Moreover in Finland, transferring into electronic matriculation exams in the spring of 2019 mandates using ICT at earlier school levels. A bunch of ICT tools, such as the computer algebra system wxMaxima, will be available [49]. Practicing with these tools should be started as early as feasible. Math could, for example, be split into normal and laboratory lessons, which would be held in the ICT lab.

What are the fundamental concepts of computer science, and how do they interact with the corresponding concepts of math?

The basic computing fundamentals are function and variable, which a novice programmer will meet even in the simplest “Hello World” example. In math, algebra and particularly functions are the areas that students find most challenging. Functions should be introduced gradually and by bridging them more closely with prior knowledge. For bridging purposes, Wilkie uses multiple presentations, for example, sequences and visual graphs [44].

By proceeding towards functions and variables in the zone of proximal learning [43], calculators may be used as variable/function tutors by explicitly highlighting the connection between variable x as an input and function keys as functions producing an output of y . Probably a student encounters an explicit variable the first time when he is looking at ‘ x ’ in a calculator keyboard. To deepen the understanding of variables, one needs information about the memory architecture of a computer. ICT education should contain the basics of computer architecture including data storage and memory. In this context storing variables in memory should be evoked.

Even if syntactic nuances exist, a variable in math is a straightforward concept compared with a variable in ICT, where the dual nature (a value - an address) complicates it. Furthermore, a variable in programming may be of the non-numeric type, such as a string. In mathematical functions, one input value that is typically a real value results in one and only one output value, also a real value. On the other hand, functions in programming have a wider variety. First, they inherit the ambiguity due to variables as parameters that may be passed by value or by reference, or are of a non-numeric type. Secondly, functions may return a different value with the same input based on the internal state. Thirdly, they may return no value at all.

What ICT topics are left uncovered in the current FNC, when compared with the discrete computing curriculum of the UKNC?

Compared with UKNC computing syllabus there is a multitude of computer-related skills that are left uncovered without a dedicated subject and teacher. For example, security issues, the basics of computer and network architecture and overall fluency with technology are nowadays comparable with civic competences. In addition, computers may also be used as creativity tools, e.g. design and web-based authoring (blogs, vlogs), and they provide lots of options for developing multi-literacy, for example, content creation, media editing and digital literacy skills. Overall, preparedness for further studies may be strengthened by intelligent searches, source criticism, data analysis and data visualization skills. Explicit knowledge building might be done with mapping tools. Lonka [25] petitions, "Besides fun and practical activities, it is crucial to facilitate deep learning through guided engagement in scientific inquiry, expert-like designing; in short, students’ deliberate efforts to build, create, and synthesize knowledge."

Computer science needs skills taught in other subjects as well; mathematics alone is not enough. Still, many areas and new developments in ICT do not fit in to traditional school subjects. It is to be expected that the pace of innovation will continue to speed up in the future – for example, cloud based artificial intelligence is rapidly emerging as a production quality provider of applications of a totally new kind. Since the world is rapidly being digitized, including ICT as a separate subject should be seriously considered. Furthermore, it would also serve as a placeholder for future needs and new developments in technology education.

Future considerations

Whether ICT should be taught alongside extended math, as a separate subject, or as a combination, it should be studied in practice with various learning experiments. As Lonka [25] points out, “ In Finland and many other countries the availability of technology is adequate, but the primary challenge to overcome is the readiness deficiency for the pedagogically meaningful use of ICT. It is imperative to develop innovative pedagogies that simultaneously support the acquisition of a deep knowledge base, understanding, and 21st Century skills. ”

In addition, different programming paradigms and languages should be compared with novice students in order to find the pedagogically sound and working alternative. For instance, the UKNC curriculum leaves these open and just talks about “low-level” and “high-level” languages and learning at least two of them [6]. In addition, the short-term hypes of certain programming languages and applications should not influence curriculum planning. Instead, it ought to rest on the fundamentals common to all programming paradigms, whether imperative, functional, or object-oriented.

To lessen the cognitive load in the beginning, visual programming languages such as Scratch, and interactive environments using interpretive languages, should be favored [34]. We advocate progressing from a more disciplined to a looser direction only after orthodox coding conventions, such as modularity, have been internalized. Functional languages are highly disciplined and hence promoted by a few of the ICT establishment. However, the Racket coding school (2016 spring) held in Finland received contradictory feedback from the participating teachers as it was regarded as being too complex [28]. In the UK, the CAS community recommends the path of Scratch-JavaScript-Python, which, for the sake of coding discipline, should preferably be Scratch-Python-Racket. Even if JavaScript were removed to prevent students from developing inappropriate coding conventions, web programming would mandate it. However, if the object-oriented nature of Scratch were recognized and used as a bridge to the most popular object-oriented language to maximize the benefit, then this sequence would stand as Scratch-

Python-Java. If it ain’t chickens, it’s feathers - the golden egg of ICT teaching is yet to be determined.