К анализу широтно-импульсной системы с обратной связью

Широтно-импульсные системы (ШИС) находят применение в устройствах автоматического регулирования (управления), а также в усилителях мощности класса D с промежуточной широтно-импульсной модуляцией, охваченных отрицательной обратной связью для уменьшения нелинейных искажений. Наличие обратной связи в ШИС неизбежно связано с проблемой обеспечения устойчивости. Решение этой проблемы в виде, приемлемом для практического применения, для ШИС в общем случае не существует. Возможности частных решений были рассмотрены в [1; 2].

Необходимо провести поиск новых методов анализа устойчивости ШИС, применимых в практических приложениях.

Методы анализа широтно-импульсных систем. Анализ импульсных систем производится, как правило, на базе теории решетчатых функций и дискретного преобразования Лапласа [1]. Теория амплитудно-импульсных систем (АИС) в настоящее время разработана достаточно подробно как для линейного тракта, так и для систем, содержащих нелинейные безынерционные элементы [1; 2].

В отличие от АИС, ШИС значительно труднее поддается анализу, поэтому их исследуют путем сведения к эквивалентным нелинейным АИС (рис. 1)

Согласно [2] уравнение системы (см. рис. 1) в решетчатых функциях имеет вид x (n, 0) = f (n, 0) - BT x n=1Y xZ Ф(x)jS(т)ю(n - m -1,1 - т)dT,(1)

m=00

τ где т = т - дискретное время; В - коэффициент линейного усиления x(t) в тракте АИС.

Интеграл в (1) представляет собой свертку функции формирующего элемента и импульсной характеристики ю ( t ). В [2] он получил название приведенной импульсной характеристики ю п ( t ) .

Если уравнение ШИС удается свести к (1) (рис. 2), то к ней можно применить все известные методы анализа и расчета нелинейных АИС.

Для ШИС функция формирующего элемента 5 ( t ) имеет вид, представленный на рис. 3, где Т - период тактовой частоты и 5 (т) соответствует двусторонней широтноимпульсной модуляции (ШИМ). При K 1 = 0, или K 2 = 0 имеет место односторонняя ШИМ.

По аналогии с (1), для ШИС можно записать следующее выражение:

x ( n ,0) = f ( n ,0) - BT x

Ф 1 ( х ) = K ₂(1 - х ), ф₂( х ) = K 1 + K 1 х , K 1 + K ₂ = 1. (3) Введем понятие коэффициента асимметрии ШИМ:

А = K K ,

K 1 + K ₂

K 1 = Н А ., K 2 = — .         (4)

2           2 _

На интервале интегрирования в (2) 5 (т) = 1, а ю ( n - m - 1;

1 - т) можно представить рядом элементарных импульсных характеристик:

ю ( n - m - 1,1 - т) =

5 r v -1

=ZZ с;

v =0 ц=0

( n - m - т/ ц !

x exp q_v ( n - m - т)

где 5 - число разных полюсов; r - кратность v -го полюса;

( rv ^- ц ^{- 1})

C' =----1--d-----x vц    (rv -ц-1)! dq(rv-ц-1)

x

P h ( q ) . tQ h ( q )

( q - q v ) r^v

q = qv

Р _н( q ); Q _н( q ) - полиномы в числителе и знаменателе передаточной функции непрерывной части ШИС W ( q ) .

Предположим, что все полюса простые и не равны нулю (наличие нулевых или кратных полюсов не усложняет и не упрощает задачи сведения ШИС к АИС).

Для случая простых полюсов

с ;= C v = 1 W ( q )( q - q . ) q = qv -

^{n - 1} ГФ? (x)

x Z [ ²   S ( т )m( n - m - 1,1 - т) dr .

m =0^J Ф 1 < X)

ю ( n - m - 1,1

-

s

т) = Z C v exp q v ( n - m - т) .

В отличие от (1) интеграл в (2) является функцией x(t), что и определяет особенности анализа ШИС. Согласно рис. 3, v=1

Подставляя (6) в (2), получим

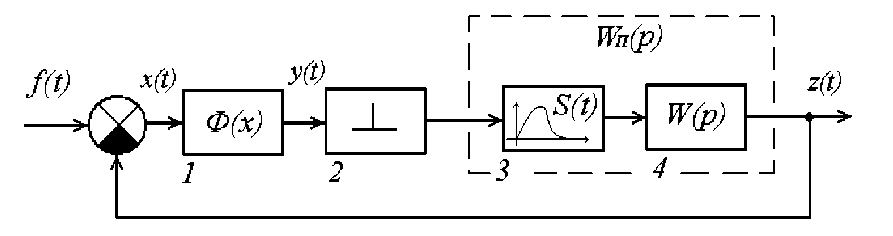
Рис. 1. Структурная схема нелинейной АИС: f ( t ), z ( t ) - соответственно входной и выходной сигналы; w ( t ) - импульсная характеристика непрерывной (линейной) части ШИС; у - длительность импульса; x ( t ) - сигнал ошибки; y ( t ) - нелинейное преобразование x ( t ); 1 - нелинейные безынерционные преобразователи тракта; 2 - генератор тактовых 8 -функций, модулированных по амплитуде сигналом y ( t ); 3 - генератор импульсов формы 5 ( t ); 4 - линейная часть тракта.

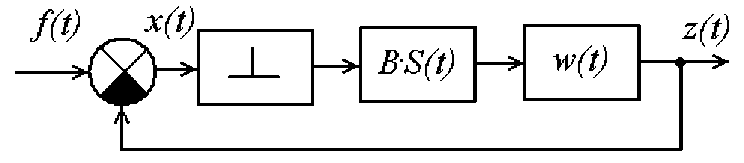
Рис. 2. Упрощенная структурная схема ШИС

x ( n , 0) = f ( n , 0) -

-

n -1 , Ъ< * >

■ BT E E J exp -qv т d т x xC 'v exp [ qv (n - m)] =

= f(n, 0)-BT E {E Фv [x(m,0)] wnv(n-m)L m=0 v=1

где

., (7)

ф ₂ [ ^x ( ^m ,0)^]

Ф v [ x ( m , 0) ] = J exp фД x ⁽ m ,°)^]

- q v т d т

w v = C ' v ^ex p [ q v ^{( n -} m ) ] - ⁽⁹⁾

Сравнивая (7) и (1), можно сделать вывод, что ШИС сводится к эквивалентной многомерной нелинейной АИС, а число параллельных ветвей эквивалентной АИС равно числу корней характеристического уравнения.

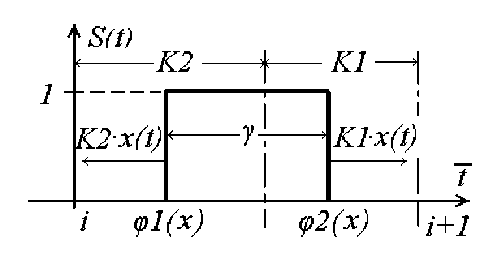
Рис. 3- Формирующий элемент ШИС

Анализ многомерных нелинейных АИС позволяет определить в общем виде лишь абсолютную устойчивость системы, причем приемлемые для практики результаты удается получить лишь для двумерных систем или для систем, сводящихся к двумерным при анализе устойчивости [3].

В связи с этим при анализе устойчивости ШИС прибегают к приближенным методам, позволяющим снизить порядок эквивалентной АИС. Например, в [4] предлагается представить Ф _у ( x ) степенным полиномом вида

N

Ф v ( x ) = E r kv ) x ^k -                   (10)

k =1

В этом случае (7) принимает вид x (n ,0) = f (n ,0) -

- BT E E E C ‘ v exp [ q_v ( n - m ) ] x ^k ( m ,0) = m =0 v =1 k =1

n -1 N

= f ( n ,0) - BT E E x ^k ( m ,0) ® П k ( n - m ),     (11)

m =0 k =1

где гёП v(n - m ) = Erv ’C'v exp [ qv(n - m)]-    (12)

v =1

Сопоставляя (7) и (11), нетрудно заметить, что в (11) число ветвей определяется числом членов полинома (10), из которых одна ветвь - линейная.

Если эквивалентная нелинейность Ф ( x ) относительно мала, то в полиноме (10) можно оставить лишь два-три слагаемых. При этом эквивалентная АИС будет двух- или трехмерной даже в случае высоких порядков линейной части ШИС .

Если

Ф v ( x ) = r v ) • x + r ₂ ⁽ v ) • x ², то, как показано в [4], структурная схема ШИС может быть сведена к одномерной нелинейной АИС.

Такой метод приближенного анализа устойчивости особенно эффективен, когда нелинейность эквивалентной АИС выражена слабо.

Анализ устойчивости ШИС методом искусственного понижения порядка её линейной части. В основу этого метода анализа положен способ приближенного расчета переходных процессов в сложных линейных цепях, предложенный и детально исследованный Я. С. Ицхоки [5]. Его суть заключается в следующем.

Порядок исходного дифференциального уравнения линейной части системы искусственно понижается (дифференциальное уравнение укорачивается), а в описание системы вводится эквивалентное запаздывание (в некоторых случаях возможно и незапаздывающее решение). Параметры укороченного уравнения подбираются таким образом, чтобы крутизна нарастания переходной функции h ( t ) в междецильном пространстве (МП) и амплитуда колебательного процесса (если он есть) соответствовали исходной h ( t ) (рис. 4) .

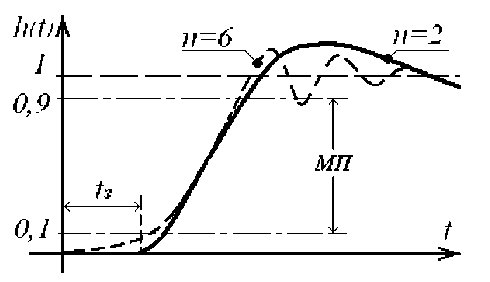
Рис. 4. Аппроксимация переходной характеристики

Такой способ может быть весьма эффективен даже при понижении сложных линейных цепей высокого по- рядка до первого-второго порядка.

Для решения задачи приближенного описания линейной части ШИС ее передаточную функцию следует привести к нормированному виду:

2                    n

W ( p ) = ^{1 +} g 1 p ⁺ g 2 p ⁺ - ⁺ g n p ,

1 + a1 p + a 2 p2 +... + akp где по крайней мере n < k - 1 (при n > k - 1 аппроксимации запаздывающей функцией не существует).

Искомая аппроксимация W(p) порядка m отыскивает- ся в виде

W ( p ) =__^__ ,

^{4 }} 1+ b ; p + b 2 p ² + ... + b m p m

^^^^^^^.

где t определяется решением следующего уравнения: m+1        m t з -      ^зт + L + (-1) m+1 •Am+1 = 0.

m !

Здесь

^A 1 = ^a 1 ^- g 1 ,

^A 2 = a 2 ^{- g} 2 ^- a 1 • ^g 1 ,

^A 3 = a 3 ^- g 3 ^- a 2 • g 2 ^- a 2 • g 1 -

Заметим, что необходимое значение задержки t _з соответствует одному и притом наименьшему вещественному (всегда положительному) корню t _з = t _{з m} . Отыскать это значение непросто даже при m = 3 .

Остальные параметры аппроксимации в (12) определяются следующим образом:

K 2 + K 1 X

Ф 1 [ X ( m , 0 ) ] = I exp

K 2 ( 1- X )

τ b ₁

dr =

= ^b 1

1 / exp b" ( K 2 + K1X )

-

exp

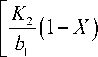
b1' = A1 - tзт , t2 зт b2   A 2 A1 Чт +2 | ,

где X – нормированный сигнал, изменяющийся в пределах 0 <  X < 1. С учетом (4) выражение (14) можно переписать следующим образом:

2m b' = —m--m± +  m-2 t3т - ...  +(-1)mhs..

^m             1!2! m !

Ф 1 ( X ) = 2 b 1 exp

1 2 b ₁

exp

AX , X sh.

2 b 1 J    2 b 1

Для аппроксимации того или иного порядка имеются определенные условия существования.

Так, приближение порядка m = 0 существует всегда.

A 2   1

Приближение m = 1 ограничено условием — 2 <  2 •

В случае m = 2 возможны два варианта:

- приближения m = 1 не существует, т. е. A 2 >  0,5 — 12 . Тогда условие существования приближения m = 2 имеет вид

Графики этой зависимости для частного случая

b ₁ = 0,5 показывают, что, как и следовало ожидать, при несимметричных видах ШИМ ( А = ± 1) нелинейность Ф₁( x ) выражена значительно сильнее, чем при А = 0 (рис. 5) .

—3 <—2 - L

— 3 A 2 3

– приближение m = 1 существует, но точность приближения недостаточна. Тогда условие существования приближения m = 2 принимает вид

^A 3 < — 3

-

--1--

1 — 2A2, —2 .

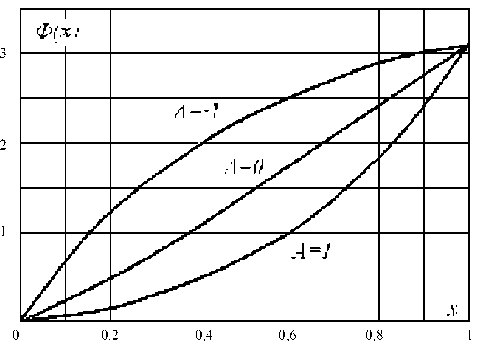
Рис. 5. Нелинейные характеристики ШИС

11—21

2 (— 2 J

— 2    1 ( — 2 1

+

3 A 1    4 (A f J

В связи с тем что повышение порядка аппроксимации резко усложняет задачу отыскания приближенного решения и анализа устойчивости ШИС, по-видимому, не следует использовать m > 2.

Предположим, что в результате применения рассмотренного выше метода аппроксимации определена передаточная функция линейной части ШИС в виде приближения первого порядка ( m = 1):

exp [ ^- Pt З1 ] _ 1 exp [ ^- Pt З1 ]

^{1 ( P} )       1 + b' P      b'         i "

^{1 p +} $

Соответствующая решетчатая (дискретная) импульсная характеристика на основании (6) примет вид

w (n - m - k, k - т -11 ) =

Передаточную функцию приведенной линейной части найдем дискретным преобразованием Лапласа от (13):

w:( q ,0 ) =

exp

-

I(1 - t)

¹ exp [ q ] - exp

1 b ₁

Заменив в этом выражении q на j ю (и = « Т), получим амплитудно-фазовую характеристику приведенной линейной части ШИС. Используя эту характеристику, можно оценить устойчивость ШИС с помощью одного из известных критериев, например критерия абсолютной устойчивости положения равновесия [2]:

= —exp b 1

- b- (n - m - k)

exp

- T (k -' - t1)

¹ + Re

B

exp

-

b ₁

σ

¹ exp [ jw ] - exp

где t 1 =

t ¹ ; b = b ’ ;

_T 1 _T

k выбирается таким, чтобы дискрет-

ное время k - т - 1 1 >  0.

Приведенная импульсная характеристика в соответствии с (9) может быть записана в виде

где о =

д Ф 1 ( x ) д x

max

1 b ₁

> 0,

– максимальное дифференциально е

значение коэффициента передачи эквивалентного нели-

w n 1 = г exp b ₁

- b- (n - m -1)

exp

- ^ ( 1 - 1 1 ) . (13)

нейного элемента; В – коэффициент линейного усиления в импульсном тракте ШИС.

Нелинейность эквивалентной АИС найдем согласно (8):

Таким образом, метод приближенного расчета переходных процессов, предложенный Я. С. Ицхоки [5], по-

зволяет существенно упростить задачу анализа устойчивости широтно-импульсной системы даже в случае высокого порядка ее линейной части.